实数（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　 在数学中，实数是可以用来度量连续的一维量（如长度、时间或温度）的数。在这里，“连续” 意味着数值对之间可以有任意小的差异。\(^\text{[a]}\) 每一个实数都可以通过一个无限小数展开来几乎唯一地表示。\(^\text{[b]}\)

　　 实数在微积分（以及数学的许多其他分支）中是基础性的，尤其体现在其在极限、连续性和导数等经典定义中的作用。\(^\text{[c]}\)

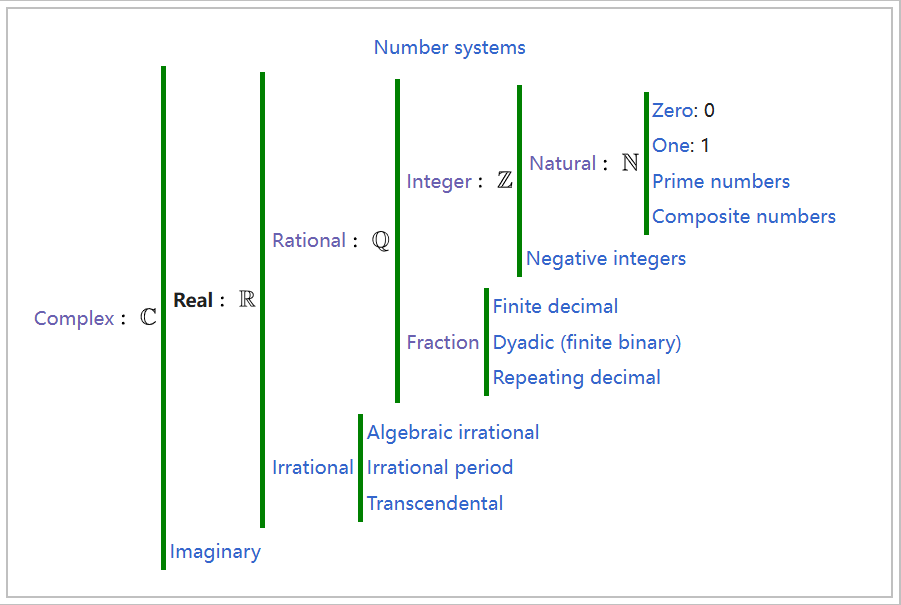
　　 实数集有时被称为 “the reals”（实数），传统上记作黑体 R，通常使用黑板粗体符号 ⁠ $\mathbf{R}$⁠。\(^\text{[1][2]}\)“实数” 这一形容词在 17 世纪由勒内·笛卡尔使用，用以区别实数与虚数（如 −1 的平方根）。\(^\text{[3]}\)

　　 实数包括有理数，例如整数 −5 和分数 $4/3$。其余的实数称为无理数。一些无理数（以及所有有理数）是具有整系数多项式的根，例如平方根 $\sqrt{2} = 1.414...$；这些数被称为代数数。而也存在一些并非如此的实数，例如 $\pi = 3.1415...$；这些数被称为超越数。\(^\text{[3]}\)

图
图 1：实数可以被看作数轴上的所有点。

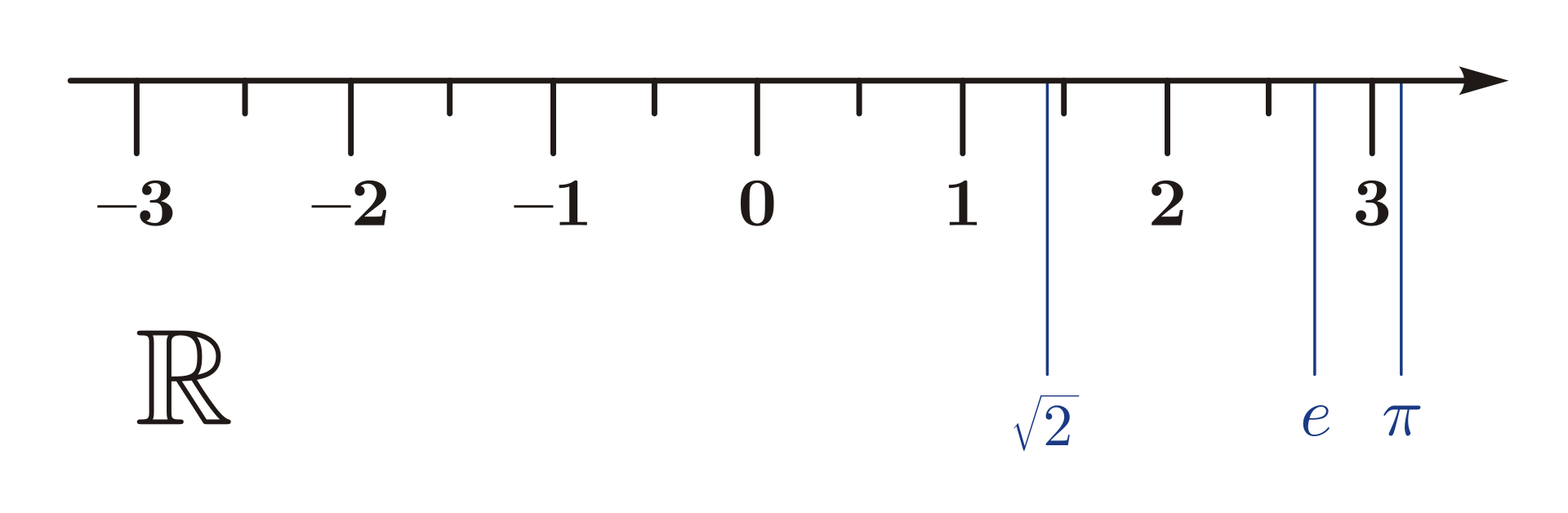
　　 实数可以被看作位于一条称为数轴或实数轴上的所有点，其中对应于整数（…，−2，−1，0，1，2，…）的点是等间距的。

　　 上述关于实数的非正式描述并不足以保证涉及实数的定理证明的严谨性。人们逐渐认识到需要一个更精确的定义，并发展出这样的定义，这是 19 世纪数学中的一项重大进展，也是实分析（研究实函数和实数值数列的数学分支）的基础。一个当前的公理化定义是：实数构成唯一的（同构意义下）Dedekind 完备有序域。\(^\text{[d]}\)

　　 实数的其他常见定义还包括：有理数的 Cauchy 数列的等价类、Dedekind 切割以及无限小数展开。这些定义都满足公理化定义，因此是等价的。

1. 刻画性质

　　 实数的完整刻画来自于它们的基本性质，可以总结为：它们构成一个 Dedekind 完备的有序域。这里，“完整刻画” 的意思是，在任意两个 Dedekind 完备有序域之间存在唯一的同构，因此它们的元素具有完全相同的性质。这意味着人们可以运算和操作实数，而无需知道它们是如何被定义的；事实上，在 19 世纪下半叶出现第一个形式化定义之前，数学家和物理学家已经这样做了几个世纪。关于这些形式化定义及其等价性的证明，详见实数的构造。

2. 算术

　　 实数构成一个有序域。直观上，这意味着初等算术的方法和规则对实数成立。更精确地说，实数上定义了两个二元运算（加法与乘法）以及一个全序关系，并且满足以下性质：

　　 从上述性质中可以推导出许多其他性质。特别是：

辅助运算

　　 还有一些常用的运算，可以由前述性质推导而来：

辅助序关系

　　 上文所述的全序关系记作 $a< b$ 读作 “a 小于 b”。另外还有三种常用的序关系：

整数与分数作为实数

　　 实数 $0$ 和 $1$ 通常被视为与自然数 $0$ 和 $1$ 相同。这使得可以将任意自然数 $n$ 识别为 $n$ 个等于 1 的实数之和。

　　 这一识别方式可以继续推广：一个负整数 $-n$（其中 $n$ 为自然数）可被视为与实数 $n$ 的加法逆元 $-n$ 相同。类似地，一个有理数 $\tfrac{p}{q}$（其中 $p, q$ 是整数且 $q \neq 0$）被视为对应于实数 $p$ 与 $q$ 的商。

　　 通过这种识别方式，有理数集合 $\mathbb{Q}$ 成为实数集合 $\mathbb{R}$ 的一个有序子域。下面将要介绍的 Dedekind 完备性意味着某些实数（如 $\sqrt{2}$）不是有理数；它们被称为无理数。

　　 上述识别是合理的，因为自然数、整数和实数通常并不是通过它们各自的 “本性” 来定义的，而是通过它们的定义性性质（公理）来刻画的。因此，将自然数与某些实数对应起来是合理的，因为这些实数满足 Peano 公理，其中 “加 1” 被视为后继函数。

　　 形式上，我们有以下单射同态：从自然数 $\mathbb{N}$ 到整数 $\mathbb{Z}$ 的有序幺半群单射同态；从整数 $\mathbb{Z}$ 到有理数 $\mathbb{Q}$ 的有序环单射同态；从有理数 $\mathbb{Q}$ 到实数 $\mathbb{R}$ 的有序域单射同态。这些识别的实质在于不区分每个单射同态的定义域和像，因此我们写作： $$ \mathbb{N} \subset \mathbb{Q} \subset \mathbb{R}.~ $$ 严格来说，这些识别是一种记号上的滥用（因为形式上，一个有理数是整数对的等价类，而一个实数是 Cauchy 数列的等价类），但通常是无害的。只有在非常特定的情境下，必须避免这种简化，并明确使用上述同态。例如，在构造性数学和计算机编程中就是如此。在编程的情况下，这些同态通常被解释为类型转换，而编译器往往可以自动完成这些转换。

3. Dedekind 完备性

　　 前述性质并不能区分实数与有理数。这一区别由 **Dedekind 完备性** 提供，其内容是：每个有上界的非空实数集都存在一个最小上界。其含义如下：设实数集 $S$ 若存在实数 $u$ 使得对所有 $s \in S$ 都有 $s \leq u$，则称 $u$ 是集合 $S$ 的一个上界。因此，Dedekind 完备性意味着：如果 $S$ 非空且有上界，则它必然存在一个小于任意其他上界的上界，即最小上界。

　　 Dedekind 完备性不仅蕴含了其他类型的完备性（见下文），还带来一些重要推论：

　　 最后两个性质可以概括为：实数构成一个实封闭域。这进一步意味着代数学基本定理的实数版本，即：每个实系数多项式都可以分解为次数不超过二的实系数多项式的积。

4. 小数表示

　　 描述实数最常见的方法是通过它的小数表示，即一串十进制数字，每个数字代表一个介于 0 到 9 之间的整数与十的幂的乘积。这种表示在小数点左边延伸有限位（对应正的十的幂），在小数点右边则延伸无限位（对应负的十的幂）。对于一个小数表示在小数点左边延伸 $k$ 位的实数 $x$，标准记法是：$b_{k}b_{k-1}\cdots b_{0}.a_{1}a_{2}\cdots $，这里的数字按十的幂次降序排列，非负幂和负幂由小数点分隔，所表示的是如下无穷级数： $$ x = b_{k}10^{k} + b_{k-1}10^{k-1} + \cdots + b_{0} + \frac{a_{1}}{10} + \frac{a_{2}}{10^{2}} + \cdots .~ $$ 例如，圆周率常数 $\pi = 3.14159\cdots$，其中 $k=0$，$b_{0}=3$，$a_{1}=1$，$a_{2}=4$，依此类推。

　　 更严格地说，一个非负实数 $x$ 的小数表示由一个非负整数 $k$ 以及一个无限序列的数字 $$ b_{k}, b_{k-1}, \ldots , b_{0}, a_{1}, a_{2}, \ldots ~ $$ （每个数字在 0 到 9 之间）组成。（如果 $k>0$，按照约定 $b_{k} \neq 0$。）

　　 这种小数表示通过截断序列得到的小数分数的最小上界来刻画实数：给定一个正整数 $n$，在第 $n$ 位处截断序列，得到有限部分和： $$ \begin{aligned} D_{n} &= b_{k}10^{k} + b_{k-1}10^{k-1} + \cdots + b_{0} + \frac{a_{1}}{10} + \cdots + \frac{a_{n}}{10^{n}} \\ &= \sum_{i=0}^{k} b_{i}10^{i} + \sum_{j=1}^{n} a_{j}10^{-j}. \end{aligned}~ $$ 由该序列定义的实数 $x$，就是这些 $D_{n}$ 的最小上界。由于 Dedekind 完备性，这个最小上界必然存在。

　　 反之，给定一个非负实数 $x$，可以通过归纳法定义它的小数表示，如下所示：定义 $b_{k}\cdots b_{0}$ 为最大的整数 $D_{0}$ 的小数表示，并且满足 $D_{0} \leq x$（这个整数的存在性来自阿基米德性质）。然后，假设归纳地已经定义了 $D_{i} \quad (i< n)$,则定义 $a_{n}$ 为最大的数字，使得 $D_{n-1} + \tfrac{a_{n}}{10^{n}} \leq x$,并设 $D_{n} = D_{n-1} + a_{n}/10^{n}$.

　　 可以利用实数的定义性质证明：$x$ 是所有 $D_{n}$ 的最小上界。因此，所得到的数位序列被称为 $x$ 的小数表示。

　　 另一种小数表示可以通过在上述构造中将 $\leq x$ 替换为 $< x$ 得到。这两种表示是相同的，除非 $x$ 是形如 $\frac{m}{10^{h}}$ 的小数。在这种情况下：在第一种小数表示中，所有 $n>h$ 的 $a_{n}$ 都为 0；而在第二种表示中，所有 $n>h$ 的 $a_{n}$ 都为 9（详见 0.999...）。

　　 综上所述，实数与小数表示之间存在一个双射，只需排除那些以无限个尾随 9 结尾的表示。

　　 上述推理可以直接推广到任意进制 $B \geq 2$,只需将 10 替换为 $B$，并将 9 替换为 $B-1$。

5. 拓扑完备性

　　 使用实数的一个主要原因，是为了使得许多数列具有极限。更正式地说，实数在度量空间或一致空间的意义下是完备的（这与上一节所述的序的 Dedekind 完备性不同）：

　　 一个实数数列 $(x_{n})$ 被称为 Cauchy 数列，如果对于任意 $\varepsilon > 0$，存在一个整数 $N$（可能依赖于 $\varepsilon$），使得当 $n, m > N$ 时，距离 $|x_{n} - x_{m}|$ 小于 $\varepsilon$。这个定义最初由柯西提出，它形式化地表达了：从某一项开始，数列中的项彼此之间会无限接近并保持接近。

　　 一个数列 $(x_{n})$ 收敛于极限 $x$，如果它的项最终会无限接近并保持接近 $x$，即对于任意 $\varepsilon > 0$，存在一个整数 $N$（可能依赖于 $\varepsilon$），使得当 $n > N$ 时，距离 $|x_{n} - x|$ 小于 $\varepsilon$。

　　 每个收敛数列都是 Cauchy 数列，而在实数中反过来也成立。这意味着实数构成的拓扑空间是完备的。

　　 有理数集则不是完备的。例如数列 $$ (1;\ 1.4;\ 1.41;\ 1.414;\ 1.4142;\ 1.41421;\ \ldots),~ $$ 其中每一项依次增加 $\sqrt{2}$ 的小数展开的一位。该数列是 Cauchy 数列，但它不收敛于任何有理数（相反，在实数中它收敛于 $\sqrt{2}$ 的正根）。

　　 实数的完备性性质是微积分，以及更一般的数学分析的基础。特别是，判断一个数列是否为 Cauchy 数列，可以用来证明该数列存在极限，而无需直接计算，甚至无需知道极限的具体值。

　　 例如，指数函数的标准级数 $$ e^{x}=\sum_{n=0}^{\infty}\frac{x^{n}}{n!}~ $$ 对任意实数 $x$ 都收敛于一个实数，因为部分和 $$ \sum_{n=N}^{M}\frac{x^{n}}{n!}~ $$ 当 $N$ 足够大时，可以变得任意小（且与 $M$ 无关）。这证明了该数列是 Cauchy 数列，因此收敛，从而表明 $e^{x}$ 对任意实数 $x$ 都是良好定义的。

完备有序域

　　 实数常被描述为 “完备有序域”，这一说法可以从多种角度来理解。

　　 首先，一个序可以是格完备的。但很容易看出，没有任何有序域能够是格完备的，因为它不可能拥有最大元（给定任意元素 $z$，总可以找到更大的 $z+1$）。

　　 其次，一个序可以是 Dedekind 完备的（见 § 公理化方法）。该节末尾的唯一性结论证明了在这种 “完备” 意义下使用 “the” 这一限定词的合理性。这种完备性与利用 Dedekind 切割构造实数的方式关系最为紧密，因为该构造是从一个有序域（有理数）出发，以标准方式对其进行 Dedekind 完备化。

　　 以上两种完备性的定义都忽略了域的结构。然而，一个有序群（此处是域的加法群）可以定义一个一致结构，而一致结构中也有完备性的概念；§ 完备性 中的描述就是一种特殊情况。（这里我们指的是一致空间中的完备性概念，而不是相关但更为人熟知的度量空间完备性，因为度量空间的定义本身已经依赖于对实数的刻画。）虽然并非只有 $\mathbb{R}$ 是一致完备的有序域，但 $\mathbb{R}$ 是唯一的一致完备的阿基米德域（Archimedean field）。实际上，人们常常会用 “完备阿基米德域” 来代替 “完备有序域”。每一个一致完备的阿基米德域必然也是 Dedekind 完备的（反之亦然），这就证明了在 “the complete Archimedean field” 中使用 “the” 的合理性。这种意义上的完备性与通过 Cauchy 数列构造实数最为紧密，因为它从一个阿基米德域（有理数）出发，以标准方式对其进行一致完备化。

　　 但是，“完备阿基米德域” 这一说法最初由大卫·希尔伯特使用，他所表达的却是另一种含义。他的意思是：实数构成最大的阿基米德域，即每一个其他的阿基米德域都是 $\mathbb{R}$ 的子域。因此，$\mathbb{R}$ 在这种意义下是 “完备” 的，因为任何额外的扩充都会使其不再是阿基米德域。这种完备性的意义与通过超实数构造实数最为接近，因为该构造是从包含所有有序域的一个真类（超实数）出发，再从中选取最大的阿基米德子域。

6. 基数

　　 所有实数的集合是不可数的。这意味着：虽然自然数集合 $\{1, 2, 3, 4, \ldots\}$ 和实数集合都是无限集合，但不存在一个从实数到自然数的一一对应函数。所有实数集合的基数称为连续统的基数，通常记作 $\mathfrak{c}$.它严格大于自然数集合的基数 $\aleph_{0}$（称为 Aleph-零或 Aleph-无穷小）。连续统的基数等于自然数的幂集（即自然数所有子集的集合）的基数。

　　 关于不存在一个基数严格大于 $\aleph_{0}$ 且严格小于 $\mathfrak{c}$ 的命题，被称为连续统假设。在 Zermelo–Fraenkel 集合论加选择公理（ZFC，即现代数学的标准基础）中，连续统假设既无法被证明，也无法被否证。事实上，ZFC 的某些模型满足 CH，而另一些模型则不满足。[4]

7. 其他性质

　　 作为一个拓扑空间，实数是可分的。这是因为有理数集是可数的，并且在实数中稠密。无理数在实数中同样稠密，但它们是不可数的，且与实数具有相同的基数。

　　 实数构成一个度量空间：点 $x$ 与 $y$ 之间的距离定义为 $|x-y|$。由于实数是一个全序集，它们也携带着序拓扑；由度量产生的拓扑与由序产生的拓扑是相同的，但其表述方式不同——在序拓扑中表现为有序区间，而在度量拓扑中表现为 $\varepsilon$-球。Dedekind 切割的构造使用的是序拓扑的表述，而 Cauchy 数列的构造使用的是度量拓扑的表述。实数构成一个可收缩的（因此是连通且单连通的）、可分的、完备的 Hausdorff 维数为 1 的度量空间。实数是局部紧致的，但并非紧致的。存在多种性质可以唯一刻画实数；例如，所有无界的、连通的、可分的序拓扑空间必然与实数同胚。

　　 每个非负实数在 $\mathbb{R}$ 中都有平方根，而负数则没有。这表明 $\mathbb{R}$ 上的序是由其代数结构所决定的。此外，每个奇数次的多项式至少有一个实根：这两个性质使得 $\mathbb{R}$ 成为实封闭域的典型例子。证明这一点也是代数学基本定理的一种证明的前半部分。

　　 实数携带一个典范的测度，即勒贝格测度。它是实数作为拓扑群时的 Haar 测度，并经过归一化，使得区间 $[0,1]$ 的测度为 1。存在一些实数集并非勒贝格可测，例如 Vitali 集。

　　 实数的上确界公理涉及实数的子集，因此它是一个二阶逻辑陈述。仅靠一阶逻辑无法刻画实数：Löwenheim–Skolem 定理蕴含着存在一个可数稠密子集，它在一阶逻辑中满足与整个实数集完全相同的语句。超实数集满足与 $\mathbb{R}$ 相同的一阶语句。满足与 $\mathbb{R}$ 相同一阶语句的有序域被称为 $\mathbb{R}$ 的非标准模型。这正是非标准分析能够成立的原因：在某个非标准模型中证明一个一阶语句（可能比在 $\mathbb{R}$ 中更容易），就能保证该语句在 $\mathbb{R}$ 中也为真。

　　 实数域 $\mathbb{R}$ 是有理数域 $\mathbb{Q}$ 的一个扩张域，因此 $\mathbb{R}$ 可以被看作是一个定义在 $\mathbb{Q}$ 上的向量空间。Zermelo–Fraenkel 集合论加选择公理（ZFC）保证了该向量空间存在一个基：存在一个实数集 $B$，使得每个实数都可以唯一地表示为 $B$ 中有限多个元素的线性组合，且系数仅限于有理数，并且 $B$ 中没有任何一个元素是其他元素的有理线性组合。然而，这一存在性定理纯属理论性的，因为这种基从未被明确地刻画出来。

　　 良序定理蕴含了：如果假设选择公理成立，那么实数可以被良序化；即存在一个实数上的全序，使得每个非空实数子集在这种序中都有一个最小元。（实数的标准序 $\leq$ 并非良序，因为例如开区间在这种序下没有最小元。）同样地，这种良序的存在性也纯属理论性的，因为它从未被明确地描述出来。如果在 ZF 公理之外再额外假设 $V=L$，则可以证明实数的良序是可以通过一个公式显式定义的。\(^\text{[5]}\)

　　 一个实数可能是可计算的或不可计算的；可能是算法随机的或不是；也可能是算术随机的或不是。

8. 历史

　　 简单分数大约在公元前 1000 年就已被埃及人使用；而在约公元前 600 年的吠陀经典《绳经》（Shulba Sutras，“弦法”）中，已经包含了可能是最早的 无理数的使用。早期印度数学家（如约公元前 750–690 年的 Manava）也已隐含地接受了无理性的概念，他意识到某些数（如 2 和 61）的平方根无法被精确确定。\(^\text{[6]}\)

　　 大约在公元前 500 年，由毕达哥拉斯领导的希腊数学家们也认识到 $\sqrt{2}$ 是无理数

　　 对希腊数学家而言，“数” 仅指自然数。实数被称为比例，即两个长度的比值，或等价地，一个长度用另一个称为单位长度的长度来度量。若两个长度在某个单位下都可以用整数来表示，那么它们就是可公度的，即用现代术语说，它们的比值是一个有理数。

　　 克尼多斯的欧多克索斯（Eudoxus of Cnidus，约公元前 390–340 年）给出了两个无理比例相等的定义，这与两千多年后提出的 Dedekind 切割的思想类似，只不过他未使用除将长度乘以自然数以外的任何算术运算（参见克尼多斯的欧多克索斯）。这一工作可被视为实数的第一个定义。

　　 中世纪带来了对零、负数、整数和分数的接受，首先是由印度和中国的数学家提出的，随后阿拉伯数学家也接受了这些概念。阿拉伯数学家还是最早将无理数视为代数对象的人（这得益于代数学的发展）\(^\text{[7]}\)。他们将 “数” 和 “量” 的概念融合为一个更为普遍的实数概念 \(^\text{[8]}\)。埃及数学家阿布·卡米勒·舒贾·伊本·阿斯拉姆（Abū Kāmil Shujā ibn Aslam，约 850–930）是第一个接受无理数作为二次方程解或作为方程系数的人（通常以平方根、立方根和四次方根的形式出现）\(^\text{[9]}\)。在欧洲，这类与数的单位不可公度的数被称为无理数或 surd（意为 “聋哑”）。

　　 16 世纪，西蒙·斯蒂文奠定了现代十进制记数法的基础，并坚持认为在这种表示法下，有理数与无理数之间并无区别。

　　 17 世纪，笛卡尔引入了 “实数” 一词，用来描述多项式的根，并将其与 “虚数” 区分开来。

　　 18 和 19 世纪，无理数与超越数成为研究热点。兰伯特提出了一个有缺陷的证明，试图说明 $\pi$ 不是有理数；勒让德完善了该证明 \(^\text{[10]}\)，并进一步证明 $\pi$ 不是某个有理数的平方根 \(^\text{[11]}\)。刘维尔证明了 $e$ 和 $e^2$ 都不能是整系数二次方程的根，并首次建立了超越数存在性；康托尔扩展并极大简化了该证明 \(^\text{[12]}\)。埃尔米特（Hermite，1873）证明了 $e$ 是超越数，林德曼（Lindemann，1882）证明了 $\pi$ 是超越数。林德曼的证明后来被魏尔施特拉斯（Weierstrass，1885）、希尔伯特（Hilbert，1893）、胡尔维茨 \(^\text{[13]}\) 和戈尔丹 \(^\text{[14]}\) 大大简化。

　　 古希腊人早已知道在有理数之间存在许多点，例如 $\sqrt{2}$。连续数轴的存在被认为是不言自明的，但这种连续性的本质（即今天所谓的完备性）并未被理解。几何中发展出的严谨性直到 19 世纪才被引入到数的概念之中 \(^\text{[15]}\)。

现代分析

　　 微积分的创立者在使用实数和极限时，并没有对其进行严格的定义。在其著作《分析教程》（Cours d'Analyse, 1821）中，柯西使微积分趋于严格化，但他依旧没有定义实数，并且在没有证明的情况下假设：每个柯西数列都有极限，且该极限是一个实数。

　　 1854 年，黎曼 在研究傅里叶级数方法时强调了微积分的局限性，显示出对实数进行严格定义的必要性。\(^\text{[16]: 672 }\)

　　 从 1858 年戴德金开始，数位数学家致力于实数的定义，包括汉克尔、梅雷和海涅。最终在 1872 年，出现了两个相互独立的实数定义：一个是戴德金提出的戴德金割，另一个是 康托尔提出的柯西数列的等价类。\(^\text{[17]}\)

　　 然而，这些定义仍然留下了若干未解决的问题，并导致了数学的基础危机：两个定义都假设有理数以及自然数已经被严格定义，而这直到几年后随着 Peano 公理的提出才得以完成。两个定义都涉及无限集合（戴德金割以及柯西数列的元素集），而康托尔的集合论则是在几年后才发表的。这些定义都涉及对无限集合的量化，而这无法在经典的一阶谓词逻辑中形式化。这也是 20 世纪上半叶发展高阶逻辑的原因之一。

　　 1874 年，康托尔证明了实数集是不可数无限的，而代数数集是可数无限的。康托尔最初的不可数性证明不同于他在 1891 年发表的著名的对角线论证。

9. 形式化定义

　　 实数系统 $(\mathbb{R}; +; \cdot; <)$ 可以在同构意义下以公理化方式定义，其内容如下所述。同时，也有许多方法可以构造 “实数系统”。一种常见的方法是从自然数出发，代数地定义有理数，最后将实数定义为柯西数列的等价类或戴德金割（即有理数的某些子集）\(^\text{[18]}\)。另一种方法是从欧几里得几何的某种严格公理化体系出发（例如希尔伯特或塔斯基的公理化），然后以几何方式定义实数系统。所有这些实数的构造方法都已被证明是等价的，也就是说，它们得到的数系是同构的。

公理化方法

　　 设 $\mathbb{R}$ 表示所有实数的集合。那么：

　　 最后一个性质对实数成立，但对有理数（或其他更特殊的有序域）则不成立。例如：$\{x \in \mathbb{Q} : x^{2} < 2\}$ 在有理数中有上界（例如 1.42），但没有最小的有理上界，因为 $\sqrt{2}$ 不是有理数。

　　 这些性质蕴含了阿基米德性质（这一性质并非由其他完备性的定义推出）。阿基米德性质表明：整数集在实数中没有上界。事实上，如果情况相反，则整数会有一个最小上界 $N$；那么 $N-1$ 就不是上界，因此存在一个整数 $n$，使得 $n > N-1$，于是 $n+1 > N$，这与 $N$ 的 “最小上界” 性质矛盾。

　　 实数由上述性质唯一确定。更确切地说，若给定任意两个 Dedekind 完备有序域 $\mathbb{R}_{1}$ 与 $\mathbb{R}_{2}$，则存在一个从 $\mathbb{R}_{1}$ 到 $\mathbb{R}_{2}$ 的唯一域同构。这种唯一性使我们能够把它们视为本质上相同的数学对象。

　　 关于实数的另一种公理化方法，参见塔斯基的实数公理化体系。

从有理数构造

　　 实数可以通过对有理数的完备化来构造，例如由十进制或二进制展开定义的数列（如 $3;\ 3.1;\ 3.14;\ 3.141;\ 3.1415;\ \ldots$）收敛到一个唯一的实数——在这个例子中就是 $\pi$。

　　 关于更多细节以及其他实数的构造方法，参见实数的构造。

10. 应用与联系

物理学

　　 在物理科学中，大多数物理常数（例如万有引力常数）和物理变量（例如位置、质量、速度和电荷）都用实数来建模。事实上，诸如经典力学、电磁学、量子力学、广义相对论以及标准模型等基本物理理论，都是借助于建立在实数基础上的数学结构来描述的，这些结构通常是光滑流形或 Hilbert 空间。不过，物理量的实际测量总是具有有限的精度和准确度。

　　 物理学家有时提出过这样的设想：更为基础的理论可能会用不构成连续统的量来取代实数，但这些设想目前仍然是推测性的。\(^\text{[19]}\)

逻辑

　　 实数最常见的形式化方式是基于 Zermelo–Fraenkel 集合论公理体系，但一些数学家也在其他数学逻辑基础下研究实数。特别是，实数在反演数学和构造性数学中也被研究。\(^\text{[20]}\)

　　 超实数由 Edwin Hewitt、Abraham Robinson 等人发展，它通过引入无穷小数和无穷大数来扩展实数集合，使得可以以更接近莱布尼茨、欧拉、柯西等人最初直觉的方式来建立无穷小分析。

　　 Edward Nelson 的内部集合论在语法上扩展了 Zermelo–Fraenkel 集合论，引入了一元谓词 “标准”。在这种方法中，无穷小是实数集合中的非 “标准” 元素（而不是像 Robinson 的理论中那样属于其扩展的元素）。

　　 连续统假设断言：实数集合的基数是 $\aleph_{1}$，即继 $\aleph_{0}$（整数的基数）之后的最小无穷基数。Paul Cohen 在 1963 年证明了连续统假设是集合论公理的独立公理；也就是说，人们可以在集合论中选择将其作为公理，或者选择其否定，而不会引起矛盾。

计算

　　 电子计算器和计算机无法直接对任意实数进行运算，因为有限的计算机不能存储无限多个数字或其他无限表示。它们通常甚至也不能直接处理任意可定义的实数，因为这类对象在操作上不便。

　　 相反，计算机通常使用有限精度的近似数，称为浮点数，其表示方式类似于科学记数法。可实现的精度受限于为每个数字分配的数据存储空间，无论是定点数、浮点数、任意精度数，还是其他表示形式。大多数科学计算使用二进制浮点运算，通常是 64 位表示，约能提供 16 位十进制精度。实数满足通常的算术规则，但浮点数并不完全满足。数值分析研究的就是采用近似算术实现的数值算法的稳定性和精度。

　　 另一方面，计算机代数系统可以通过操作符号公式来精确处理无理量（例如 $\sqrt{2}$、$\arctan 5$、或 $\int_{0}^{1} x^{x}\, dx$），而不是依赖于它们的有理近似或小数近似。[21] 但精确和符号算术也有其局限性：例如，它们计算开销更大；一般来说，不可能确定两个符号表达式是否相等（即常数问题）；算术运算还可能导致单个数的表示规模指数级膨胀（例如，一个有理数平方后，其分子和分母的位数大致会翻倍；一个多项式平方后，其项数也会大致翻倍），从而压垮有限的计算机存储。\(^\text{[22]}\)

　　 如果存在一种算法能够生成某个实数的数位，就称该实数是可计算的。由于算法只有可数多个，\(^\text{[23]}\) 而实数却是不可数多个，因此几乎所有实数都是不可计算的。此外，两个可计算数是否相等是一个不可判定问题。一些建构主义者只接受那些可计算的实数的存在。可定义数的集合更大一些，但它依然只是可数的。

集合论

　　 在集合论，特别是描述集合论中，Baire 空间常被用作实数的替代物，因为实数具有某些拓扑性质（如连通性），在技术上会带来不便。Baire 空间中的元素通常被称为 “实数”。

11. 词汇与符号

　　 所有实数组成的集合记作 $\mathbb{R}$（黑板粗体）或 R（正体粗体）。由于它天然具有域的结构，因此在讨论其代数性质时，常使用 “实数域” 这一表述。

　　 正实数集与负实数集通常分别记作 $\mathbb{R}^{+}, \ \mathbb{R}^{-}$，也常用 $ \mathbb{R}_{+}, \ \mathbb{R}_{-}$ 来表示。[24][25] 非负实数可以记作 $\mathbb{R}_{\geq 0}$，但人们也常将其记作 $\mathbb{R}^{+} \cup \{0\}$。 [24] 在法国数学中，正实数和负实数通常包含零，这两个集合分别记作 $\mathbb{R}_{+}, \ \mathbb{R}_{-}$[25]。在这种理解下，不含零的集合则称为严格正实数与严格负实数，分别记作 $\mathbb{R}_{+}^{*}, \ \mathbb{R}_{-}^{*}$。[25]符号 $\mathbb{R}^{n}$。

　　 表示由实数组成的 n 元组集合（实坐标空间），它可以视为 n 个 $\mathbb{R}$ 的笛卡尔积。它是一个定义在实数域上的 n 维向量空间，通常称为 n 维坐标空间；一旦选定直角坐标系，它就可与 n 维欧几里得空间相对应。在这种对应下，欧几里得空间中的一点对应于其笛卡尔坐标组成的元组。

　　 在数学中，“实” 常用作形容词，表示底层域是实数域。例如：实矩阵、实多项式、实李代数、。该词也可作名词使用，指代 “实数”（如 “全体实数的集合”）。

12. 推广与扩展

　　 实数可以从多个方向进行推广和扩展：

13. 另见

图
图 2

14. 注释

　　
a.这本身不足以区分实数与有理数；还需要一个完备性的性质。
b.非零数若有有限小数表示，则会有两种小数展开（参见 0.999...）；其他实数则只有一种小数展开。
c.极限与连续性可以在一般拓扑中不依赖实数来定义，但这些推广相对较新，且仅用于非常特定的情境。
d.更准确地说，若给定两个完备的全序域，它们之间存在唯一的同构。这意味着恒等映射是实数中唯一与序相容的域自同构。事实上，恒等映射是实数的唯一域自同构，因为 $x>y \iff \exists z \ \mid \ x-y=z^{2}$，而右侧公式在域自同构下保持不变。

15. 参考文献

引文

  1. "real". Oxford English Dictionary (第 3 版). 2008. 'real', n.2, B.4. Mathematics. A real number. Usually in plural
  2. Webb, Stephen (2018). "Set of Natural Numbers ℕ". Clash Of Symbols: A Ride Through The Riches Of Glyphs. Springer. pp. 198–199.
  3. "Real number". Encyclopedia Britannica.
  4. Koellner, Peter (2013). "The Continuum Hypothesis". In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy*. Stanford University.
  5. Moschovakis, Yiannis N. (1980), "5. The Constructible Universe", Descriptive Set Theory, North-Holland, pp. 274–285, ISBN 978-0-444-85305-9.
  6. T. K. Puttaswamy, "The Accomplishments of Ancient Indian Mathematicians", pp. 410–11. In: Selin, Helaine; D'Ambrosio, Ubiratan, eds. (2000), Mathematics Across Cultures: The History of Non-western Mathematics, Springer, ISBN 978-1-4020-0260-1.
  7. O'Connor, John J.; Robertson, Edmund F. (1999), "Arabic mathematics: forgotten brilliance?", MacTutor History of Mathematics Archive, University of St Andrews.
  8. Matvievskaya, Galina (1987), "The Theory of Quadratic Irrationals in Medieval Oriental Mathematics", Annals of the New York Academy of Sciences, 500 (1): 253–77 [254], Bibcode:1987NYASA.500..253M, doi:10.1111/j.1749-6632.1987.tb37206.x, S2CID 121416910.
  9. Jacques Sesiano, "Islamic mathematics", p. 148, in Selin, Helaine; D'Ambrosio, Ubiratan (2000), Mathematics Across Cultures: The History of Non-western Mathematics, Springer, ISBN 978-1-4020-0260-1.
  10. Beckmann, Petr (1971). A History of π (PI). St. Martin's Press. p. 170. ISBN 9780312381851.
  11. Arndt, Jörg; Haenel, Christoph (2001), Pi Unleashed, Springer, p. 192, ISBN 978-3-540-66572-4, retrieved 2015-11-15.
  12. Dunham, William (2015), The Calculus Gallery: Masterpieces from Newton to Lebesgue, Princeton University Press, p. 127, ISBN 978-1-4008-6679-3, retrieved 2015-02-17. Cantor found a remarkable shortcut to reach Liouville's conclusion with a fraction of the work.
  13. Hurwitz, Adolf (1893). "Beweis der Transendenz der Zahl e". Mathematische Annalen (43): 134–35.
  14. Gordan, Paul (1893). "Transcendenz von e und π". Mathematische Annalen. 43 (2–3): 222–224. doi:10.1007/bf01443647. S2CID 123203471.
  15. Stefan Drobot, Real numbers. Prentice-Hall, Inc., Englewood Cliffs, N.J. 1964, vii+102 页.
  16. Robson, Eleanor; Stedall, Jacqueline A., 编. (2009). The Oxford handbook of the history of mathematics. Oxford handbooks. 牛津；纽约: Oxford University Press. ISBN 978-0-19-921312-2. OCLC 229023665.
  17. O'Connor, John J.; Robertson, Edmund F. (2005 年 10 月), "The real numbers: Stevin to Hilbert", MacTutor History of Mathematics Archive, University of St Andrews.
  18. "Lecture #1" (PDF). 18.095 Lecture Series in Mathematics. 2015-01-05.
  19. Wheeler, John Archibald (1986). "Hermann Weyl and the Unity of Knowledge: In the linkage of four mysteries—the 'how come' of existence, time, the mathematical continuum, and the discontinuous yes-or-no of quantum physics—may lie the key to deep new insight". American Scientist. 74 (4): 366–75. Bibcode:1986AmSci..74..366W. JSTOR 27854250.
  20. Bengtsson, Ingemar (2017). "The Number Behind the Simplest SIC-POVM". Foundations of Physics. 47 (8): 1031–41. arXiv:1611.09087. Bibcode:2017FoPh...47.1031B. doi:10.1007/s10701-017-0078-3. S2CID 118954904.
  21. Bishop, Errett; Bridges, Douglas (1985), Constructive analysis, Grundlehren der Mathematischen Wissenschaften [数学科学基础原理], 第 279 卷, 柏林/纽约: Springer-Verlag, ISBN 978-3-540-15066-4, 第 2 章.
  22. Cohen, Joel S. (2002), Computer algebra and symbolic computation: elementary algorithms, 第 1 卷, A K Peters, p. 32, ISBN 978-1-56881-158-1.
  23. Trefethen, Lloyd N. (2007). "Computing numerically with functions instead of numbers" (PDF). Mathematics in Computer Science. 1 (1): 9–19. doi:10.1007/s11786-007-0001-y.
  24. Hein, James L. (2010), "14.1.1", Discrete Structures, Logic, and Computability (第 3 版), Sudbury, MA: Jones and Bartlett Publishers, ISBN 97-80763772062, 检索于 2015-11-15.
  25. Schumacher, Carol (1996). Chapter Zero: Fundamental Notions of Abstract Mathematics. Addison-Wesley. pp. 114–115. ISBN 9780201826531.
  26. 巴黎高等师范学院, Nombres réels ("Real numbers") [实数], 存档于互联网档案馆 Wayback Machine, 2014-05-08, 第 6 页.

16. 资料来源

外部链接

                     

© 保留一切权利