索末菲模型

贡献者： fengdalizzz; addis

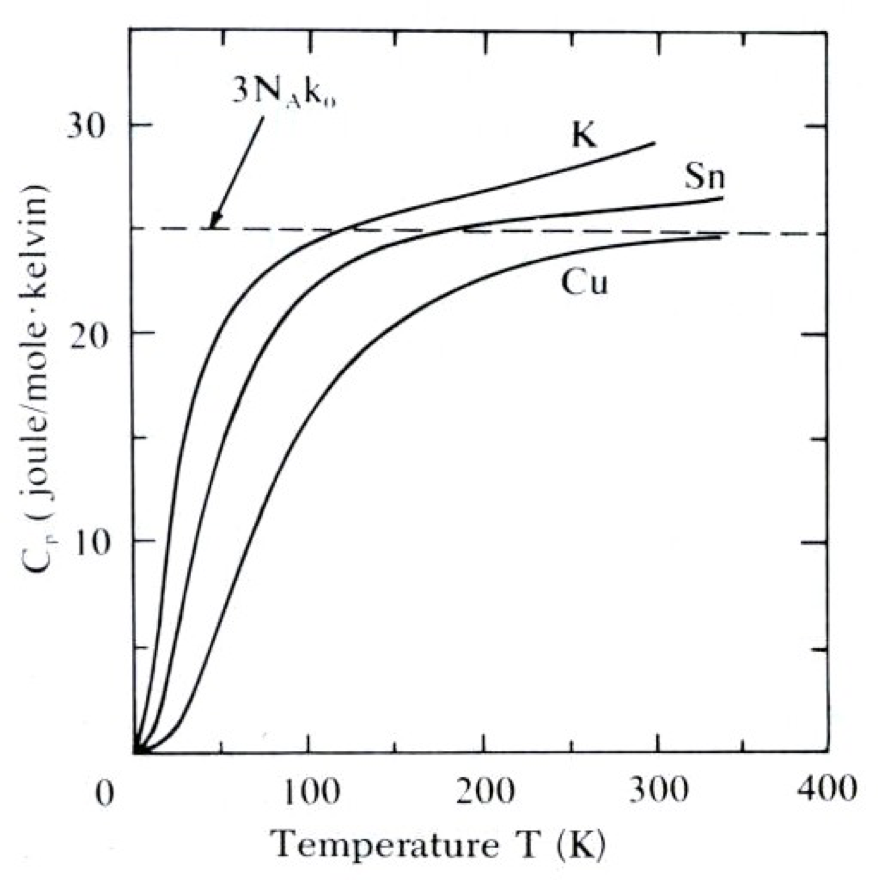
　　虽然德鲁特模型在电子的声、光和热导率方面解释得比较好，但其在解释电子比热时却遇到了困难。

　　根据经典的能均分定理，金属电子气中每个电子的平均内能为 $3k_BT/2$，对热容的贡献为 $3k_B/2$，然而实验中的电子热容几乎测不到，只有德鲁特模型给出的 1%左右，而且与温度密切相关。

图 1：常见金属热容随温度的变化

　　解释这个现象需要用到索菲亚模型。

1. 基本假设

独立电子近似（Independent electron approximation）：电子之间不会相遇，不存在任何相互作用。
自由电子近似：相对电子而言，晶体中的离子的运动忽略不计，同时也忽略电子与离子的库伦力作用。
不碰撞假设：电子以物质波的形式存在，并且不会与离子碰撞。
泡利不相容原理：电子是费米子，满足泡利不相容原理。

2. k 动量空间

　　根据上面的假设，我们可以写出电子满足的薛定谔方程：

\begin{equation} -\frac{\hbar^2}{2m}\nabla^2\psi=E\psi~, \end{equation}

方程的解是平面波 $\psi=Ae^{i \boldsymbol{\mathbf{k}} \cdot \boldsymbol{\mathbf{r}} }$。

　　为了使平面波函数归一，我们将电子限定在一个 $L^3$ 中的正方形盒子中，考虑到固体中含有大量的电子，含有大量重复的这种小盒子，所以我们认为盒子中的波函数满足周期性边界条件，即：

\begin{equation} \psi( \boldsymbol{\mathbf{r}} )=\psi( \boldsymbol{\mathbf{r}} +Le_x)=\psi( \boldsymbol{\mathbf{r}} +Le_y)=\psi( \boldsymbol{\mathbf{r}} +Le_z)~. \end{equation}

所以最终的波函数为 $\psi=L^{-3/2}e^{i \boldsymbol{\mathbf{k}} \cdot \boldsymbol{\mathbf{r}} }$，其中 $ \boldsymbol{\mathbf{k}} $ 满足：

\begin{equation} \left (k_x, k_y, k_z\right )=\frac{2\pi}{L}\left(n_x, n_y, n_z\right )~. \end{equation}

能量 $E$ 满足：

\begin{equation} E=\frac{\hbar ^2 k^2}{2m}~. \end{equation}

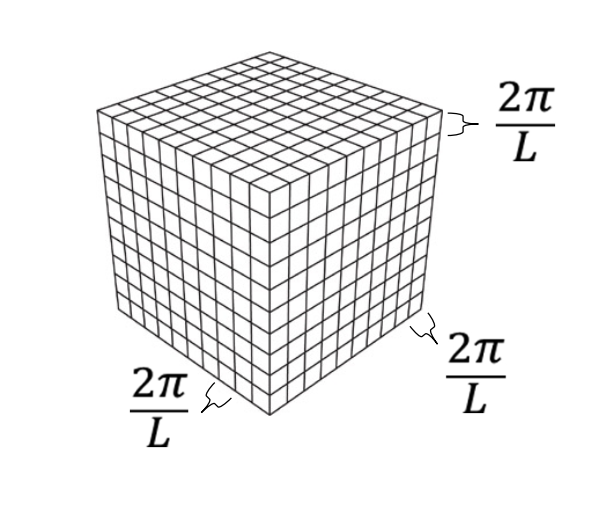
可以这么理解，每一个电子的波函数中的 $ \boldsymbol{\mathbf{k}} $ 是分立的，对应下列图片中的一个小格子。当格子足够密集时，所有能量相等的电子则可以近似对应一个 $ \boldsymbol{\mathbf{k}} $ 空间中的球面。

图 2：k 动量空间

3. 费米分布和费米能

　　由于电子是费米子，自由电子不能处在同一个状态内，即上述的 k 动量空间中一个格子内不能有超过 2 个电子（"2"是来自于电子自旋），热力学统计给出一定温度下电子的分布有：

\begin{equation} f(E)=\left ( \exp\left(\frac{E-\mu}{k_B\ T}\right) +1\right )^{-1} \in[0,1]~, \end{equation}

表征某个能量值下电子的存在几率。由于能量 $E$ 是 $ \boldsymbol{\mathbf{k}} $ 的函数，那么其自然也表明是否有电子处在某个特定的 $ \boldsymbol{\mathbf{k}} $ 上。那么总的电子数就是 $N=\textstyle \sum_{ \boldsymbol{\mathbf{k}} }2\ f( \boldsymbol{\mathbf{k}} )$。总的能量就是 $E_{sum}=\textstyle \sum_{ \boldsymbol{\mathbf{k}} }2\ E( \boldsymbol{\mathbf{k}} )f( \boldsymbol{\mathbf{k}} )$。

　　其中 $\mu$ 是化学势，其与电子总数有关，随温度缓慢变化。$\mu (T=0K)$ 称为费米能 $E_F$.

　　 $T=0K$ 时的情况非常特殊。我们先来考虑 $T=0K$ 时的情况来理解函数 $f(E)$。$T=0K$ 时的函数是一个阶跃函数：

\begin{equation} \begin{aligned} f(E)=1& & (E<\mu) \\ f(E)=0& & (E>\mu)~. \end{aligned} \end{equation}

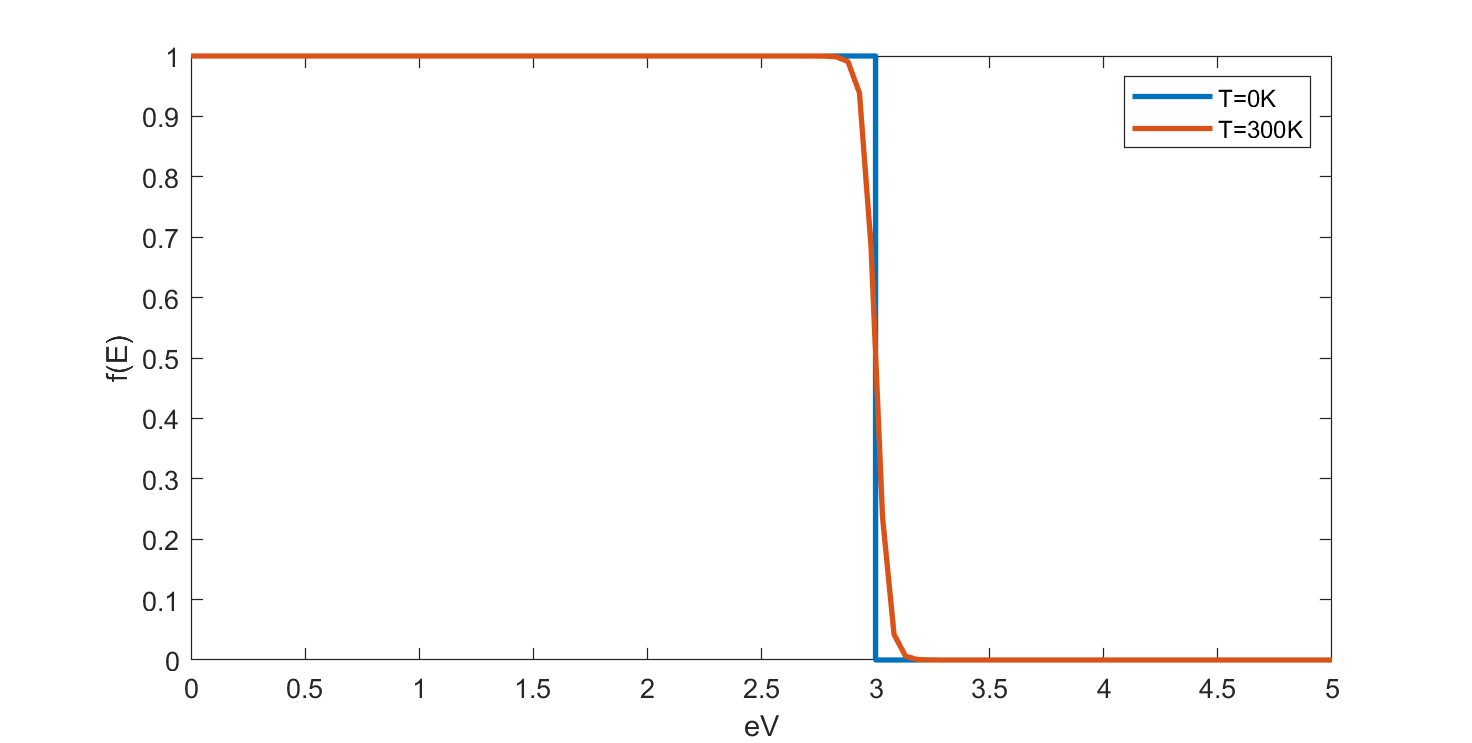
这表明电子会占满能量小于 $\mu$ 的所有格子。实验测得 $\mu(T=0K)$，即 $E_F$，大致在 2~10eV 之间，而室温 300K 对应的能量 $k_BT\approx2.59*10^{-2}\ eV$，远远小于 $E_F$ 的尺度，而前面提到 $\mu$ 是随温度缓慢变化的，则可以画出室温 300K 时的电子分布(假设 $E_F=3\ eV$)：

图 3：电子随能量的分布

　　可以发现，图像中只是 $E_F$ 附近的电子分布出现了变化，则可以推断，电子的热力学性质大致都是 $E_F$ 附近的电子分布变化导致的。

4. 求和与积分的转换、态密度

　　前面提到，电子总数和总能量有：

\begin{equation} E_{sum}=\textstyle \sum_{ \boldsymbol{\mathbf{k}} }2\ E( \boldsymbol{\mathbf{k}} )f( \boldsymbol{\mathbf{k}} )~, \end{equation}

\begin{equation} N=\textstyle \sum_{ \boldsymbol{\mathbf{k}} }2\ f( \boldsymbol{\mathbf{k}} )~. \end{equation}

　　为了能计算出电子总数与总能量的表达式，我们需要把求和形式变成积分形式。做一个简单的移动：

\begin{equation} \iiint g( \boldsymbol{\mathbf{k}} )\,dk_x\,dk_y\,dk_z=dk_x\,dk_y\,dk_z\,\sum g( \boldsymbol{\mathbf{k}} )~. \end{equation}

从图 2 就可以看出，有 $dk_x\,dk_y\,dk_z=(\frac{2\pi}{L})^3$。所以当 L 的尺度足够大，即 $(\frac{2\pi}{L})^3$ 的尺度足够小时，我们就能有：

\begin{equation} E_{sum}=\textstyle \sum_{ \boldsymbol{\mathbf{k}} }2\ E( \boldsymbol{\mathbf{k}} )f( \boldsymbol{\mathbf{k}} )=(\frac{L}{2\pi})^3\,2 \int_{ \boldsymbol{\mathbf{k}} }E( \boldsymbol{\mathbf{k}} )f( \boldsymbol{\mathbf{k}} )d^3k~, \end{equation}

\begin{equation} N=\textstyle \sum_{ \boldsymbol{\mathbf{k}} }2\ f( \boldsymbol{\mathbf{k}} )=(\frac{L}{2\pi})^3\,2 \int_{ \boldsymbol{\mathbf{k}} }f( \boldsymbol{\mathbf{k}} )d^3k~. \end{equation}

由于 $E( \boldsymbol{\mathbf{k}} )$ 和 $f( \boldsymbol{\mathbf{k}} )$ 与 k 的方向是无关的，所以上述的积分还可以再次简化成：

\begin{equation} E_{sum}=(\frac{L}{2\pi})^3\,2\int d\Omega \int E(k)f(k)k^2dk=\frac{L^3}{\pi^2} \int E(k)f(k)k^2dk~, \end{equation}

\begin{equation} N=(\frac{L}{2\pi})^3\,2\int d\Omega \int f(k)k^2dk=\frac{L^3}{\pi^2}\int f(k)k^2dk~. \end{equation}

借助 $E=\frac{\hbar^2}{2m}k^2$，可以继续化简式子变成：

\begin{equation} E_{sum}=L^3 \int E\,f(E)\,\frac{\sqrt{2m^3}}{\pi^2\hbar^3}\sqrt{E}dE~, \end{equation}

\begin{equation} N=L^3 \int f(E)\,\frac{\sqrt{2m^3}}{\pi^2\hbar^3}\sqrt{E}dE~, \end{equation}

这样就能直接在 E 空间上积分了。此外，可以定义态密度：

\begin{equation} g(E)=\frac{\sqrt{2m^3}}{\pi^2\hbar^3}\sqrt{E}~. \end{equation}

其表征 dE 范围内的量子态数目（即 k 空间中格子的数目 X2）。

5. 积分形式

　　电子数密度 $N/L^3$ 和单位体积电子气总能量 $E_{sum}/L^3$ 都有一个共同形式：

\begin{equation} \int_0^{\infty} dE\,f(E)h(E)~. \end{equation}

设 $h(E)$ 的原函数为 $Q(E)$，即 $Q(E)=\int_0^E d\epsilon\,h(\epsilon)$，则 $h(E)=Q^\prime(E)$，则有：

\begin{equation} \int_0^{\infty} dE\,f(E)h(E)=\int_0^{\infty} f(E)dQ(E)= f\,Q\bigg|_0^\infty-\int_0^{\infty} Q(E)f^\prime (E)dE~. \end{equation}

其中因为 $Q(0)=0$ 和 $f(\infty)=0$（$e^{-\infty}$ 级的无穷小比 $1/Q(\infty)$ 更高阶），所以 $f\,Q\bigg|_0^\infty=0-0=0$，所以有：

\begin{equation} \int_0^{\infty} dE\,f(E)h(E)=-\int_0^{\infty} dE\,Q(E)f^\prime (E)~. \end{equation}

我们记得 $f(E)$ 为：

\begin{equation} f(E)=\left ( \exp\left(\frac{E-\mu}{k_B\ T}\right) +1\right )^{-1}~. \end{equation}

令 $x=\frac{E-\mu}{k_B\,T}$，则 $-f^\prime(E)$ 为：

\begin{equation} -f^\prime(E)=\frac{(k_BT)^{-1}}{(e^{x/2}+e^{-x/2})^2}~. \end{equation}

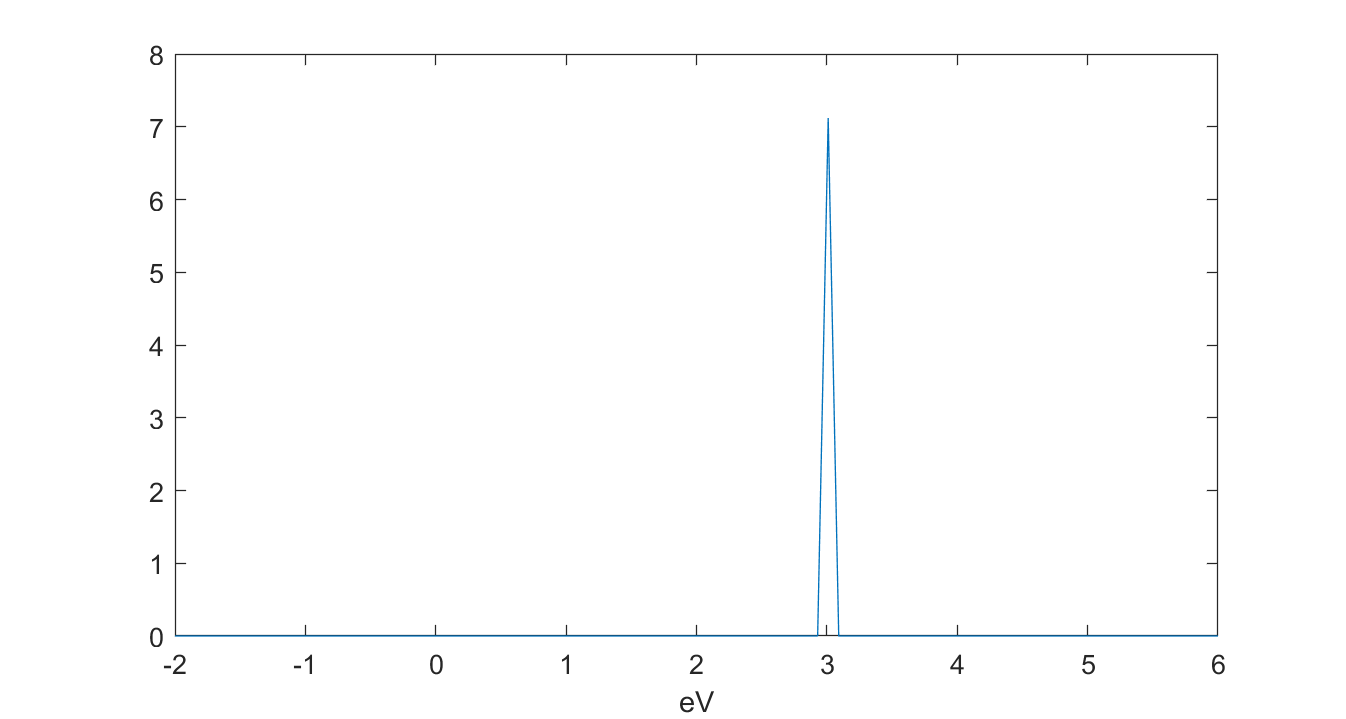
画出 $-f^\prime(E)$ 图像，可以发现其在 $E=\mu$ 附近外都非常接近 0，类似一个 $\delta$ 函数（假设 $\mu=3eV$，室温下）：

图 4：函数性质

　　所以可以将式 19 的积分下限变成 $-\infty$，将 $Q(E)$ 在 $E=\mu$ 处进行泰勒展开，保留到二阶项：

\begin{equation} Q(E)\approx Q(\mu)+Q^\prime (\mu)(E-\mu)+\frac{1}{2}Q''(\mu)(E-\mu)^2~. \end{equation}

再代回到之前的式 19 ，有：

\begin{equation} \begin{aligned} &\int_0^{\infty} dE\,f(E)h(E)=\\ &-Q(\mu)\int_{-\infty}^{\infty}f'(E)dE+Q'(\mu)k_B\,T\int_{-\infty}^{\infty}dx\frac{x}{(e^{x/2}+e^{-x/2})^2}\\ &+\frac{1}{2}Q''(\mu)(k_B\,T)^2\int_{-\infty}^{\infty}dx\frac{x^2}{(e^{x/2}+e^{-x/2})^2}~. \end{aligned} \end{equation}

　　等号右边第一项即 $-Q(\mu)\cdot f(E)\bigg|_{-\infty}^\infty=Q(\mu)$，右边第二项是奇函数的对称区间积分，所以为零，右边第三项是特殊函数的积分，结果为 $\frac{\pi^2}{6}Q''(\mu)(k_B\,T)^2$。所以总的结果为：

\begin{equation} \int_0^{\infty} dE\,f(E)h(E)=Q(\mu)+\frac{\pi^2}{6}Q''(\mu)(k_B\,T)^2~. \end{equation}

6. 电子气热性质

　　终于谈到电子气的热性质了。令 $Q(E)=\int_0^{E} g(\epsilon)d\epsilon$ 代入式 24 ，则有：

\begin{equation} \rho=N/L^3=\int_0^{\infty} dE\,f(E)g(E)=\int_0^{\mu} g(\epsilon)d\epsilon+\frac{\pi^2}{6}g'(\mu)(k_B\,T)^2~. \end{equation}

而 $g(E)=\frac{\sqrt{2m^3}}{\pi^2\hbar^3}\sqrt{E}=C\sqrt{E}$，那么积分就有一个简单的结果：

\begin{equation} \rho=\frac{2}{3}C\mu\sqrt{\mu}+\frac{\pi^2}{6}\frac{C}{2\sqrt{\mu}}(k_B\,T)^2~. \end{equation}

在非相对论条件下，改变温度，$\rho$ 不应该变化，则有：

\begin{equation} 0=C\sqrt{\mu}\frac{\partial \mu}{\partial T} -\frac{\pi^2}{6}\frac{C}{4\mu\sqrt{\mu}}\frac{\partial \mu}{\partial T}(k_B\,T)^2+\frac{\pi^2}{6}\frac{C}{\sqrt{\mu}}k_B^2 T~. \end{equation}

令 $T=0$，则可以得到 $\frac{\partial \mu}{\partial T}\bigg|_{T=0}=0$。再求一次偏导，同样令 T=0，记得 $\mu(T=0)=E_F$，则有：

\begin{equation} 0=C\sqrt{E_F}\frac{\partial ^2\mu}{\partial\, T^2}\bigg|_{T=0}+\frac{\pi^2}{6}\frac{C}{\sqrt{E_F}}k_B^2~, \end{equation}

则有 $\frac{\partial ^2\mu}{\partial\, T^2}\bigg|_{T=0}=-\frac{\pi^2}{6}\frac{k_B^2}{E_F}$。将 $\mu$ 在 $T=0$ 处进行泰勒展开，保留到二阶，即有：

\begin{equation} \mu\approx E_F\left(1-\frac{\pi^2}{12}(\frac{k_B\,T}{E_F})^2\right)~. \end{equation}

引入费米温度 $T_F$，满足 $k_B\,T_F=E_F$，则：

\begin{equation} \mu\approx E_F\left(1-\frac{\pi^2}{12}(\frac{T}{T_F})^2\right)~. \end{equation}

典型的费米温度 $T_F$ 的量级为 $10^4\thicksim 10^5$K，远远高于室温 300K，故化学势 $\mu$ 在室温下仅偏离 $E_F$ 约 $10^{-4}$，这验证了我们之前在第三节的说法。

　　令 $Q(E)=\int_0^{E} \epsilon g(\epsilon)d\epsilon$ 代入式 24 ，则有：

\begin{equation} u=E_{sum}/L^3=\int_0^{\infty} dE\,f(E)g(E)E=Q(\mu)+\frac{\pi^2}{6}Q''(\mu)(k_B\,T)^2~. \end{equation}

对 $Q(\mu)$ 在 $E=E_F$ 处进行泰勒展开，保留到一阶，并利用式 30 ，有：

\begin{equation} Q(\mu)\approx Q(E_F)+Q'(E_F)(\mu-E_F)=Q(E_F)-\frac{\pi^2}{12}g(E_F)(k_B\,T)^2~, \end{equation}

而 $Q''(\mu)=\mu g'(\mu)+g(\mu)\approx E_Fg'(E_F)+g(E_F)=\frac{3}{2}g(E_F)$. 所以有:

\begin{equation} u=E_{sum}/L^3\approx Q(E_F)+\frac{\pi^2}{6}g(E_F)(k_B\,T)^2~. \end{equation}

那么单位体积热容：

\begin{equation} c_V=\frac{\partial u}{\partial T}=\frac{\pi^2}{3}g(E_F)k_B\,T~. \end{equation}

电子密度：

\begin{equation} \rho=\frac{2}{3}C\mu\sqrt{\mu}+\frac{\pi^2}{6}\frac{C}{2\sqrt{\mu}}(k_B\,T)^2\approx \frac{2}{3}g(E_F)E_F~. \end{equation}

则单个电子的热容即为：

\begin{equation} c=\frac{c_V}{\rho}=\frac{\pi^2}{2}\frac{T}{T_F}k_B~. \end{equation}

　　前面提到实验中测得的电子热容是德鲁特模型预言的 $3k_B/2$ 的 1$\%$ 左右，而 $T_F$ 是室温的 100 倍左右，$\frac{\pi^2}{2}\frac{T}{T_F}k_B$ 恰好是 $3k_B/2$ 的 1$\%$ 左右，符合实验结果。同样其也预言温度较低时，固体呈现量子效应，热容随温度大致成线性关系。索末菲模型和德拜 T3 定律一并解释了图 1 中的实验测量结果。