东南大学 2001 年 考研 量子力学

                     

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1.（15 分）

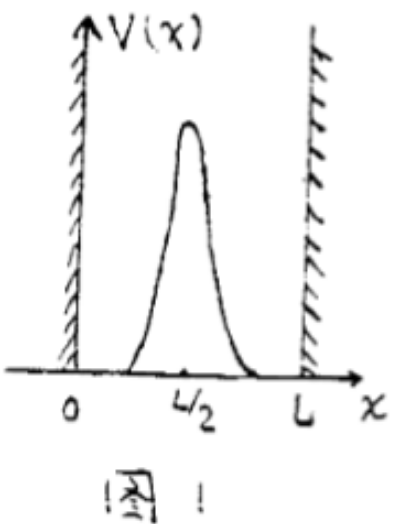
　　 质量为 $m$ 的粒子，被无限深方势阱束缚在 $0 < x < L$ 区域中作一维运动，粒子同时受到位于势阱中心、强度为 $\gamma$ 的 $\delta$ 势作用。阱内区域的 Schrödinger 方程为： \[ -\frac{\hbar^2}{2m}\frac{d^2 }{dx^2}\psi(x) + \gamma \delta \left(x - \frac{L}{2}\right)\psi(x) = E \psi(x)~ \] 求第一基态能量 $E$ 满足的超越方程（用 $m$、$\gamma$、$L$ 表达）。

2.（15 分）

　　 设 $t=0$ 时,粒子的状态为 \[\psi(x) = A \left( \sin^3 kx + \frac{1}{2} \cos kx \right)~\] 求此时粒子的平均动量和平均动能。

3.（15 分）

　　 考虑哈密顿量为 \[H = \frac{p^2}{2m} + \frac{m \omega^2 x^2}{2}~\] 的一维谐振子

1. 求出 “初始位置” 和 “初始动量” 的算子： \[ x_0 = x \cos \omega t - \frac{p}{m \omega} \sin \omega t~ \] \[ p_0 = p \cos \omega t + m \omega x \sin \omega t~ \] 的期待值对时间的依赖关系。
2. 这两了算子与哈密顿量对易吗?
3. 在海森堡表象中算子的运动去程为何!

4.（15 分）

　　 测量一个电子（处于自由空间）自旋的 $z$ 分量发现是 $\frac{\hbar}{2}$

1. 接着测量自旋的 $X$ 分量,可能得到什么结果?
2. 得到这些结果的几率是多少?
3. 如果测是自旋方向的轴与 $z$ 轴成 $\delta$ 角,各种可能值的几率是多少?
4. 在 c) 中自旋测量期望值是多少？

5.（20 分）

　　 设带电粒子在均匀磁场 $\vec{B}$ 和各个同性谐振子势 $V(r) = \frac{1}{2}m\omega^2 r^2$ 中运动，求线量本证值。

6.（20 分）

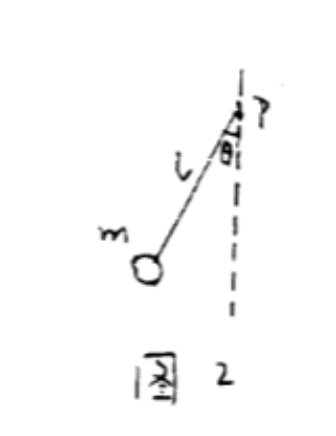
　　 一根长为 $l$ 无质量的细绳，一端固定于支点 $P$，另一端系质量 $m$。在重力作用下，质点在竖直平面内摆动，如图 2 所示：

1. 在小角近似下求系统能级。
2. 求由于小角近似的误差而产生的基态能量最低阶修正.