素数定理（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在数学中，素数定理描述了素数在正整数中的渐近分布情况。它形式化地表达了一个直观的观点：随着数值的增大，素数变得越来越稀疏，并且精确地量化了这一稀疏现象发生的速度。

　　 该定理由雅克·阿达马和夏尔·让·德拉瓦莱-普桑于 1896 年各自独立证明，所用的方法基于伯恩哈德·黎曼引入的一些思想，尤其是黎曼ζ函数。最早发现的分布形式为：$\pi(N) \sim \frac{N}{\log N}$ 其中，$\pi(N)$ 表示素数计数函数，即不超过 $N$ 的素数个数，$\log N$ 是 $N$ 的自然对数。这意味着对于足够大的 $N$，从不超过 $N$ 的整数中随机选一个数是素数的概率大约为 $1 / \log N$。换句话说，在前 $N$ 个整数中，相邻两个素数之间的平均间隔大约为 $\log N$。

　　 因此，一个最多有 $2n$ 位数的随机整数（当 $n$ 足够大时）成为素数的可能性，大约是一个最多有 $n$ 位数的随机整数的一半。例如，在所有最多有 1000 位的正整数中，大约每 2300 个数中有一个是素数（因为 $ \log\left(10^{1000}\right) \approx 2302.6$）；而在最多有 2000 位的正整数中，大约每 4600 个数中才有一个是素数（因为 $ \log\left(10^{2000}\right) \approx 4605.2$）。

1. 定理的表述

图
图 1：该图显示了素数计数函数 $\pi(x)$ 与其两个近似函数 $x / \log x$ 和 $\mathrm{Li}(x)$ 的比值。随着 $x$ 的增大（注意：横轴为对数刻度），这两个比值都趋近于 1。其中，$\pi(x) / (x / \log x)$ 的比值从上方非常缓慢地收敛，而 $\pi(x) / \mathrm{Li}(x)$ 的比值则从下方收敛得更快。

　　 设 $\pi(x)$ 为素数计数函数，定义为不超过实数 $x$ 的素数个数，例如 $\pi(10) = 4$，因为有四个素数（2, 3, 5 和 7）不超过 10。

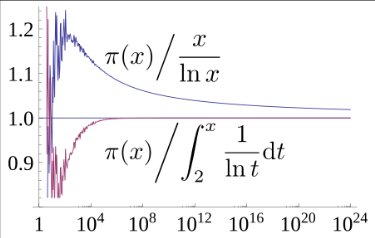
　　 那么，素数定理指出：$\frac{x}{ \log\left(x\right) }$ 是 $\pi(x)$ 的一个良好近似，其含义是，当 $x$ 趋于无穷大时，函数 $\pi(x)$ 与 $\frac{x}{ \log\left(x\right) }$ 的商的极限为 1，即： $$ \lim_{x \to \infty} \frac{\pi(x)}{\left[\frac{x}{ \log\left(x\right) }\right]} = 1~ $$ 这被称为素数分布的渐近法则。

　　 使用渐近记号，该结果可重新表述为： $$ \pi(x) \sim \frac{x}{\log x}~ $$ 这里的渐近记号（以及该定理）并不表示 $\pi(x)$ 与 $\frac{x}{\log x}$ 的差在 $x$ 趋于无穷大时有极限，而是表示后者对前者的相对误差趋近于 0。

图
图 2：对数-对数图显示了 $x / \log x$ 与 $\mathrm{Li}(x)$ 这两个对素数计数函数 $\pi(x)$ 的近似所产生的绝对误差。与比值不同的是，$\pi(x)$ 与 $x / \log x$ 之间的差值会随着 $x$ 的增大而无限增长。另一方面，$\mathrm{Li}(x) - \pi(x)$ 的符号会无限次地发生变化。

　　 素数定理等价于如下陈述：第 $n$ 个素数 $p_n$ 满足： $$ p_n \sim n \log\left(n\right) ~ $$ 这里的渐近记号同样表示：当 $n$ 趋于无穷大时，该近似的相对误差趋于 0。例如，第 $2 \times 10^{17}$ 个素数是 8512677386048191063，而 $(2 \times 10^{17}) \log\left(2 \times 10^{17}\right) $ 的值为约 7967418752291744388，相对误差约为 6.4%。 另一方面，以下渐近关系在逻辑上是等价的 \(^\text{[5]: 80–82 }\)： $$ \lim_{x \to \infty} \frac{\pi(x) \log x}{x} = 1, \quad \text{以及} \quad \lim_{x \to \infty} \frac{\pi(x) \log \pi(x)}{x} = 1.~ $$ 如下面将要概述的，素数定理也等价于以下公式： $$ \lim_{x \to \infty} \frac{\vartheta(x)}{x} = \lim_{x \to \infty} \frac{\psi(x)}{x} = 1,~ $$ 其中 $\vartheta(x)$ 和 $\psi(x)$ 分别是第一和第二切比雪夫函数。

　　 还等价于： $$ \lim_{x \to \infty} \frac{M(x)}{x} = 0,~ $$ 其中： $$ M(x) = \sum_{n \leq x} \mu(n)~ $$ 是梅滕斯函数，$\mu(n)$ 是莫比乌斯函数 \(^\text{[5]: 92–94 }\)。

2. 素数渐近分布定律的证明史

　　 根据安东·费尔克尔和尤里·维加编制的素数表，阿德里安-马里·勒让德在 1797 年或 1798 年猜想，素数计数函数 $\pi(a)$ 可由函数 $a / (A \log a + B)$ 近似，其中 A 和 B 是未具体说明的常数。在他 1808 年出版的第二版《数论》一书中，他提出了更精确的猜想，设定 $A = 1$，$B = -1.08366$。卡尔·弗里德里希·高斯大约在 1792 或 1793 年、年仅 15 或 16 岁时，也考虑过同样的问题（这是他 1849 年回忆中提到的）。1838 年，彼得·古斯塔夫·勒热讷·狄利克雷提出了他自己的近似函数，即对数积分 $\mathrm{li}(x)$（以略有不同的级数形式，并与高斯通信交流）。勒让德与狄利克雷的公式都蕴含了前文所述的猜想：$\pi(x)$ 与 $x / \log\left(x\right) $ 渐近等价，尽管后来的研究发现，如果从差值（而非比值）角度来看，狄利克雷的近似要显著更好。

　　 1848 年和 1850 年，俄国数学家帕夫努季·切比雪夫发表了两篇论文，试图证明素数分布的渐近规律。他的工作值得注意之处在于引入了黎曼ζ函数 $\zeta(s)$（实数 $s$ 的情形），类似于莱昂哈德·欧拉早在 1737 年的用法。切比雪夫的论文早于黎曼 1859 年著名的论文，他成功地证明了一个稍弱的形式：如果极限 $\lim_{x \to \infty} \pi(x) / (x / \log x)$ 存在，那么该极限值必定等于 1\(^\text{[7]}\)。此外，切比雪夫无条件地证明了该比值对充分大的 $x$ 被夹在两个常数之间，即：$0.92129 < \frac{\pi(x)}{x / \log x} < 1.10555$\(^\text{[8][9]}\)。尽管切比雪夫的论文尚未给出素数定理的完整证明，但他对 $\pi(x)$ 的估计已足以证明 “伯特兰猜想”：对于任意整数 $n \geq 2$，在区间 $(n, 2n)$ 内必定存在至少一个素数。

　　 关于素数分布的一个重要论文是黎曼于 1859 年发表的回忆录《论小于给定大小的素数的数量》（“On the Number of Primes Less Than a Given Magnitude”），这是他在该领域唯一发表的一篇论文。黎曼在文中引入了一些新的思想，最重要的是：素数的分布与复变函数扩展下的黎曼ζ函数的零点密切相关。特别地，正是在这篇论文中，他首次提出将**复分析方法应用于研究实数函数 $\pi(x)$ 的思想。

　　 在黎曼的思想基础上，雅克·阿达玛 \(^\text{[1]}\) 和 夏尔-让·德拉瓦莱-普桑 \(^\text{[2]}\) 各自独立地找到了素数分布渐近定律的证明，两者均发表于 1896 年。这两个证明都使用了复分析方法，证明的关键步骤是：黎曼ζ函数 $\zeta(s)$ 在所有形如 $s = 1 + it$（其中 $t > 0$）的复数点上都不为零 \(^\text{[10]}\)。

　　 20 世纪，这一定理便被称为素数定理。此后人们又发现了多种不同的证明方法，其中包括**阿特勒·塞尔伯格 \(^\text{[11]}\) 与保罗·艾狄胥 \(^\text{[12]}\) 于 1949 年提出的 “初等” 证明。这些初等证明不依赖于复分析，但仍然结构复杂。阿达玛和德拉瓦莱-普桑的原始证明过程冗长繁复，后来有学者借助托伯定理加以简化，尽管如此，仍然难以完全消化。

　　 1980 年，美国数学家唐纳德·J·纽曼 \(^\text{[13][14]}\) 发现了一个简短的证明。这个证明被认为是目前已知最简洁的素数定理证明，尽管它不是 “初等” 的，因为它使用了复分析中的柯西积分定理。

3. 证明概要

　　 以下是根据特伦斯·陶的一次讲座中提到的素数定理（PNT）证明概要 \(^\text{[15]}\)。像大多数关于素数定理的证明一样，该证明首先将问题重新表述为一个更易处理但直觉性较弱的素数计数函数的形式。核心思想是通过给素数（或相关集合，如素数的幂）加权，从而构造一个在渐进行为上更平滑的函数。最常见的这种广义计数函数是**切比雪夫函数** $\psi(x)$，其定义如下： $$ \psi(x) = \sum_{k \geq 1} \sum_{\substack{p^k \leq x\\ p \text{ 为素数}}} \log p~ $$ 有时也写作： $$ \psi(x) = \sum_{n \leq x} \Lambda(n)~ $$ 其中 $\Lambda(n)$ 是 冯·芒戈尔特函数，定义如下： $$ \Lambda(n) = \begin{cases} \log p & \text{若 } n = p^k \text{，其中 } p \text{ 是素数且 } k \geq 1 \\ 0 & \text{否则} \end{cases}~ $$ 接下来，我们可以比较容易地证明，素数定理等价于如下断言： $$ \lim_{x \to \infty} \frac{\psi(x)}{x} = 1~ $$ 这个结论可以通过以下两个估计式导出：

　　 首先上界： $$ \psi(x) = \sum_{\substack{p \leq x \\ p \text{ 为素数}}} \log p \left\lfloor \frac{\log x}{\log p} \right\rfloor \leq \sum_{\substack{p \leq x \\ p \text{ 为素数}}} \log x = \pi(x) \log x~ $$ 然后下界，使用大 O 符号（即渐近符号）表示，对于任意 $\varepsilon > 0$： $$ \psi(x) \geq \sum_{\substack{x^{1-\varepsilon} \leq p \leq x \\ p \text{ 为素数}}} \log p \geq \sum_{\substack{x^{1-\varepsilon} \leq p \leq x \\ p \text{ 为素数}}} (1 - \varepsilon)\log x = (1 - \varepsilon)\left(\pi(x) + O(x^{1-\varepsilon})\right)\log x~ $$ 通过上述上下界的估计，就可以看出 $\psi(x)$ 与 $x$ 渐近等价，从而导出素数定理的结论。

　　 下一步是寻找 $\psi(x)$ 的一个有用表示式。

　　 设 $\zeta (s)$ 为黎曼 $\zeta$ 函数。可以证明，$\zeta (s)$ 与冯·芒戈尔特函数 $\Lambda(n)$ 之间存在如下关系，因此也与 $\psi(x)$ 相关： $$ - \frac{\zeta'(s)}{\zeta(s)} = \sum_{n=1}^{\infty} \Lambda(n)\, n^{-s}~ $$ 对该等式及 $\zeta$ 函数的相关性质进行精细分析（使用梅林变换和佩龙公式），可以推出：当 $x$ 不是整数时，成立如下公式： $$ \psi(x) = x - \log\left(2\pi\right) - \sum_{\rho:\, \zeta(\rho) = 0} \frac{x^{\rho}}{\rho}~ $$ 其中求和范围为所有 $\zeta$ 函数的零点（包括平凡零点和非平凡零点）。这个令人惊艳的表达式是数论中的著名显式公式之一，它已经暗示了我们想要证明的结果：右边首项为 $x$，正是 $\psi(x)$ 的主项阶数，其后为阶数较低的修正项。

　　 证明的下一步涉及对 $\zeta$ 函数零点的研究。平凡零点为 $-2, -4, -6, -8, \dots$，可以单独处理，它们对 $\psi(x)$ 的影响为： $$ \sum_{n=1}^{\infty} \frac{1}{2n\, x^{2n}} = -\frac{1}{2} \log\left(1 - \frac{1}{x^2}\right)~ $$ 该表达式在 $x$ 很大时趋于 0，可忽略不计。

　　 而非平凡零点，即 $\zeta (s)$ 在临界带 $0 \leq \text{Re}(s) \leq 1$ 上的零点，如果存在实部为 1 的零点（即 Re(ρ) = 1），则对应的 $x^\rho$ 项将与主项 $x$ 同阶，从而影响 $\psi(x)$ 的渐近性。因此，为了完成证明，我们必须说明所有 $\zeta$ 函数的非平凡零点都满足： $$ \text{Re}(\rho) < 1~ $$ 这一步至关重要，是素数定理成立的核心条件之一。

在 Re(s) = 1 上的非零性

　　 为此，我们首先默认以下事实：$\zeta(s)$ 在半平面 $\operatorname{Re}(s) > 0$ 是一个亚纯函数，在 $s = 1$ 处有一个简单极点，在其余点处解析；并且在 $\operatorname{Re}(s) > 1$ 区域满足如下欧拉乘积公式： $$ \zeta(s) = \prod_p \frac{1}{1 - p^{-s}}~ $$ 该乘积公式是基于整数唯一素因数分解定理，说明 $\zeta(s)$ 在该区域绝不会为零，因此其对数是良定义的，并且有： $$ \log \zeta(s) = -\sum_p \log\left(1 - p^{-s}\right) = \sum_{p,\,n} \frac{p^{-n s}}{n}~ $$ 令 $s = x + i y$，则有： $$ |\zeta(x + i y)| = \exp\left( \sum_{n,\,p} \frac{ \cos\left(n y \log p\right) }{n p^{n x}} \right)~ $$ 我们使用以下恒等式： $$ 3 + 4 \cos \phi + \cos 2\phi = 2(1 + \cos \phi)^2 \geq 0~ $$ 因此可以得出： $$ \left| \zeta(x)^3 \, \zeta(x + i y)^4 \, \zeta(x + 2i y) \right| = \exp\left( \sum_{n,\,p} \frac{3 + 4 \cos\left(n y \log p\right) + \cos\left(2n y \log p\right) }{n p^{n x}} \right) \geq 1~ $$ 对所有 $x > 1$ 都成立。

　　 假设现在 $\zeta(1 + i y) = 0$。由于 $\zeta(s)$ 在 $s = 1$ 有一个简单极点，可以确定 $y \neq 0$。我们考虑 $x > 1$，并让 $x \to 1^+$。因为 $\zeta(x)$ 在 $x \to 1^+$ 时发散（趋向于无穷大），而 $\zeta(x + 2i y)$ 在该区域保持解析，所以上式左边趋于 0，与右边 $\geq 1$ 的不等式矛盾。 因此，$\zeta(s)$ 在 $\operatorname{Re}(s) = 1$ 上没有零点。

　　 由此我们可以得出结论：素数定理（PNT）在直觉上是正确的。但要严格完成这个证明，还需克服一些技术难点，主要是因为在显式公式中关于 $\zeta$ 函数零点的求和不是绝对收敛的，而只是条件收敛，并且以 “主值” 的形式存在。针对这一点有多种解决方法，其中多数依赖于精细的复分析估计。参考资料中的 Edwards 所著的书 \(^\text{[16]}\) 中详细提供了这些细节。另一种解决方式是使用 Ikehara 的 Tauber 定理，不过这个定理本身的证明也相当复杂。数学家 D.J. Newman 注意到：在素数定理的证明中其实不需要 Ikehara 定理的全力形式，只需要一个较易证明的特例即可。

4. 纽曼对素数定理的证明

　　 D. J. Newman 给出了一个快速证明素数定理（PNT）的方法。该证明由于依赖复分析，因此被视为 “非初等” 的，但只使用了该领域入门课程中的基础技巧：柯西积分公式、柯西积分定理和复积分估计。下面是该证明的简要概述，完整细节请参考文献 \(^\text{[14]}\)。该证明采用与上一节相同的初步步骤，但不是使用函数 $\psi$（即第二类切比雪夫函数），而是使用切比雪夫函数： $$ \vartheta(x) = \sum_{p \leq x} \log p~ $$ 它是通过从 $\psi$ 的级数中去除某些项得到的。类似于前一节（如 Tao 讲义中）所用的论证，可以证明： $$ \vartheta(x) \leq \pi(x) \log x~ $$ 且对任意 $0 < \varepsilon < 1$，有： $$ \vartheta(x) \geq (1 - \varepsilon)\left(\pi(x) + O(x^{1 - \varepsilon})\right) \log x~ $$ 因此，素数定理等价于如下极限成立： $$ \lim_{x \to \infty} \frac{\vartheta(x)}{x} = 1~ $$ 同样，Newman 并不直接使用： $$ -\frac{\zeta'(s)}{\zeta(s)}~ $$ 而是改用函数： $$ \Phi(s) = \sum_{p \leq x} \log p \cdot p^{-s}~ $$ 这是通过从 $-\zeta'(s)/\zeta(s)$ 的级数中去除一些项得到的。函数 $\Phi(s)$ 与 $-\zeta'(s)/\zeta(s)$ 的区别是它们的差在 $\operatorname{Re}(s) = 1$ 上是全纯的函数。由于上一节中已经证明 $\zeta(s)$ 在直线 $\operatorname{Re}(s) = 1$ 上没有零点，因此： $$ \Phi(s) - \frac{1}{s - 1}~ $$ 在 $\operatorname{Re}(s) = 1$ 上没有奇点。

　　 Newman 证明中还需要一条额外信息——这也是其简明方法中的估计关键：函数 $\vartheta(x)/x$ 是有界的。这可以通过 Chebyshev 提出的一种巧妙且简洁的方法来证明。

　　 分部积分可以揭示切比雪夫函数 $\vartheta(x)$ 与函数 $\Phi(s)$ 之间的关系。对于满足 $\operatorname{Re}(s) > 1$ 的复数 $s$，有： $$ \Phi(s) = \int_{1}^{\infty} x^{-s} \, d\vartheta(x) = s \int_{1}^{\infty} \vartheta(x)\, x^{-s-1} \, dx = s \int_{0}^{\infty} \vartheta(e^{t})\, e^{-st} \, dt~ $$ Newman 的方法通过研究如下积分是否收敛来证明素数定理（PNT）： $$ I = \int_{0}^{\infty} \left( \frac{\vartheta(e^{t})}{e^{t}} - 1 \right) \, dt~ $$ 若该积分 $I$ 收敛，则意味着被积函数在 $t \to \infty$ 时趋于 0，也就等价于素数定理的陈述。一般来说，不定积分的收敛并不保证被积函数在无穷远处趋于 0，因为其可能震荡。然而，在本例中由于 $\vartheta(x)$ 是单调递增的，因此很容易证明其极限存在。

　　 为了证明 $I$ 收敛，对满足 $\operatorname{Re}(z) > 0$ 的复数 $z$，定义函数： $$ f(t) = \frac{\vartheta(e^{t})}{e^{t}} - 1~ $$ 并定义： $$ g_T(z) = \int_{0}^{T} f(t)\, e^{-zt} \, dt,\quad\quad g(z) = \int_{0}^{\infty} f(t)\, e^{-zt} \, dt~ $$ 则有： $$ \lim_{T \to \infty} g_T(z) = g(z) = \frac{\Phi(s)}{s} - \frac{1}{s - 1},\quad\quad \text{其中 } z = s - 1~ $$ 这个表达式表示的是在直线 $\operatorname{Re}(z) = 0$ 上的一个全纯函数。

　　 要证明积分 $I$ 收敛，即证明素数定理，只需证明： $$ \lim_{T \to \infty} g_T(0) = g(0)~ $$ 这一步涉及到换序极限的问题，即： $$ \lim_{T \to \infty} \lim_{z \to 0} g_T(z) = \lim_{z \to 0} \lim_{T \to \infty} g_T(z)~ $$ 因此，该证明被归类为一种 Tauberian 定理 的应用。

　　 差值 $g(0) - g_T(0)$ 可通过柯西积分公式表示，并通过对被积函数进行估计来证明当 $T$ 足够大时该差值很小。我们固定常数 $R > 0$ 和 $\delta > 0$，使得函数 $g(z)$ 在如下区域中是全纯的： $$ |z| \leq R \quad \text{且} \quad \operatorname{Re}(z) \geq -\delta~ $$ 令 $C$ 表示该区域的边界。由于 $0$ 位于该区域的内部，柯西积分公式可得： $$ g(0) - g_T(0) = \frac{1}{2\pi i} \int_C \left( g(z) - g_T(z) \right) \frac{dz}{z}~ $$ 进一步引入 Newman 提出的一个因子 $F(z)$，得到： $$ g(0) - g_T(0) = \frac{1}{2\pi i} \int_C \left( g(z) - g_T(z) \right) F(z) \frac{dz}{z}~ $$ 其中， $$ F(z) = e^{zT} \left( 1 + \frac{z^2}{R^2} \right)~ $$ 这个因子 $F(z)$ 是整函数，且满足 $F(0) = 1$，因此不会改变该积分的值。

　　 为了估计该积分，将轮廓 $C$ 分成两部分：$C = C_+ + C_-$ 其中： $$ C_+ = C \cap \{ z \mid \operatorname{Re}(z) > 0 \}, \quad C_- = C \cap \{ \operatorname{Re}(z) \leq 0 \}~ $$ 于是可以将差值表示为： $$ g(0) - g_T(0) = \int_{C_+} \int_T^\infty H(t, z)\,dt\,dz - \int_{C_-} \int_0^T H(t, z)\,dt\,dz + \int_{C_-} g(z)F(z) \frac{dz}{2\pi i z}~ $$ 其中： $$ H(t, z) = f(t) e^{-tz} F(z)/2\pi i~ $$ 由于 $\vartheta(x)/x$ 有界，因而 $f(t)$ 也有界，设 $B$ 是 $|f(t)|$ 的一个上界。

　　 再结合如下估计： $$ |F(z)| \leq 2 \exp\left(T \operatorname{Re}(z)\right) |\operatorname{Re}(z)|/R \quad \text{（当 } |z| = R \text{ 时）}~ $$ 可以得出第一个积分的绝对值满足：$\leq B/R$ 第二项中沿 $C_-$ 的被积函数是整函数，因此根据柯西积分定理，我们可以将 $C_-$ 修改为左半平面内的一个半圆，而不改变积分值。和第一个积分类似的估计可得其绝对值也满足：$\leq B/R$ 最后，令 $T \to \infty$，由于 $e^{zT} \to 0$（从而 $F(z) \to 0$）在该轮廓上，所以第三个积分趋于 0。

　　 结合这三项可得： $$ \limsup_{T \to \infty} \left| g(0) - g_T(0) \right| \leq \frac{2B}{R}~ $$ 因为这个估计对任意 $R > 0$ 成立，令 $R \to \infty$ 即得： $$ \lim_{T \to \infty} g_T(0) = g(0)~ $$ 从而得到素数定理（PNT）成立。

5. 用对数积分表示的素数计数函数

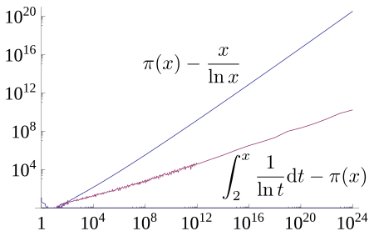
　　 在其 1838 年论文《论无穷级数在数论中的应用》的一份重印本上，Dirichlet 用手写笔记标注了一个猜想，并寄给了高斯。这个猜想（以级数而非积分的形式出现）指出，对素数计数函数 $\pi(x)$ 的一个更精确的近似是修正对数积分函数 $\operatorname{Li}(x)$，其定义为： $$ \operatorname{Li}(x) = \int_{2}^{x} \frac{dt}{\log t} = \operatorname{li}(x) - \operatorname{li}(2)~ $$ 实际上，这个积分公式强烈暗示了一个思想：在 $t$ 附近的素数 “密度” 应当近似为 $1/\log t$。

　　 该函数与对数函数的关系可以通过以下渐近展开式表达： $$ \operatorname{Li}(x) \sim \frac{x}{\log x} \sum_{k=0}^{\infty} \frac{k!}{(\log x)^k} = \frac{x}{\log x} + \frac{x}{(\log x)^2} + \frac{2x}{(\log x)^3} + \cdots)~ $$ 因此，素数定理也可以表述为：$\pi(x) \sim \operatorname{Li}(x)$ 事实上，在 1899 年的另一篇论文中 \(^\text{[17]}\)，de la Vallée Poussin 证明了： $$ \pi(x) = \operatorname{Li}(x) + O\left(x e^{-a \sqrt{\log x}}\right) \quad \text{当 } x \to \infty~ $$ 其中 $a$ 是某个正数，$O(\cdots)$ 表示大 O 符号。

　　 这个结果后来被改进为： $$ \pi(x) = \operatorname{li}(x) + O\left(x \exp\left(-\frac{A (\log x)^{3/5}}{(\log \log x)^{1/5}}\right)\right)~ $$ 其中：$A = 0.2098$\(^\text{[18]}\)

　　 到了 2016 年，Timothy Trudgian 给出了 $\pi(x)$ 与 $\operatorname{li}(x)$ 之间差的一个显式上界： $$ \left| \pi(x) - \operatorname{li}(x) \right| \leq 0.2795 \cdot \frac{x}{(\log x)^{3/4}} \cdot \exp\left(-\sqrt{\frac{\log x}{6.455}}\right)~ $$ 对于所有满足 $x \geq 229$ 的 $x$ 成立 \(^\text{[19]}\)。

　　 黎曼ζ函数与素数计数函数 $\pi(x)$ 之间的联系，是黎曼猜想在数论中极为重要的一个原因：一旦黎曼猜想被证明为真，将能提供远优于当前已知结果的素数定理误差估计。

　　 更具体地说，Helge von Koch 在 1901 年证明 \(^\text{[20]}\)，如果黎曼猜想成立，则上述近似中的误差项可以改进为： $$ \pi(x) = \operatorname{Li}(x) + O\left(\sqrt{x} \log x\right)~ $$ （事实上，这个估计与黎曼猜想是等价的。）

　　 在 1976 年，Lowell Schoenfeld 假设黎曼猜想成立，给出了大 O 符号中常数的估计值 \(^\text{[21]}\)： $$ \left| \pi(x) - \operatorname{li}(x) \right| < \frac{\sqrt{x} \log x}{8\pi} \quad \text{对于所有 } x \geq 2657~ $$ 他还对 Chebyshev 的素数计数函数 $\psi(x)$ 导出了类似的上界： $$ \left| \psi(x) - x \right| < \frac{\sqrt{x} (\log x)^2}{8\pi} \quad \text{对于所有 } x \geq 73.2~ $$ 这个后者的界限已被证明表现出一种 “方差–均值幂律”（在将其视为定义在整数上的随机函数时），也被认为对应于 $\frac{1}{f}$ 噪声，并与 Tweedie 复合泊松分布相关（Tweedie 分布是尺度不变分布族，是中心极限定理的一类推广下的聚合点 \(^\text{[22]}\)）。

　　 另一方面，J. E. Littlewood 在假设黎曼猜想成立的前提下，推导出了一个下界 \(^\text{[23][24][25]}\)： $$ \left| \pi(x) - \operatorname{li}(x) \right| = \Omega\left( \sqrt{x} \cdot \frac{\log \log \log x}{\log x} \right)~ $$

　　 对 “小” 值的 $x$ 来说，对数积分函数 $\operatorname{li}(x)$ 的值大于 $\pi(x)$。这是因为它在某种意义上不是在 “数素数”，而是在数素数的幂：即将一个素数的幂 $p^n$ 按照 $\frac{1}{n}$ 的权重计为 “$\frac{1}{n}$ 个素数”。因此可以推测 $\operatorname{li}(x)$ 通常应当比 $\pi(x)$ 大大约：$\frac{1}{2} \operatorname{li}(\sqrt{x})$ 特别地，这暗示 $\operatorname{li}(x)$ 应该始终大于 $\pi(x)$。然而，1914 年，Littlewood 证明了：$\pi(x) - \operatorname{li}(x)$ 会改变符号无穷多次。[23]也就是说，虽然 $\operatorname{li}(x)$ 一般较大，但最终总会有一些 $x$ 满足 $\pi(x) > \operatorname{li}(x)$。第一个满足 $\pi(x) > \operatorname{li}(x)$ 的 $x$ 值大约在 $x \sim 10^{316}$ 附近，详情可参阅 Skewes 数相关条目。（另一方面，偏移对数积分函数 $\operatorname{Li}(x)$ 在 $x = 2$ 就已经小于 $\pi(x)$：事实上，$\operatorname{Li}(2) = 0$，而 $\pi(2) = 1$。）

6. 初等证明

　　 在 20 世纪上半叶，一些数学家（特别是 G. H. Hardy）相信，在数学中存在一个根据证明所涉及数的类型（整数、实数、复数）而形成的证明方法等级体系，而素数定理之所以 “深奥”，正是因为它依赖复分析 \(^\text{[9]}\)。然而，这一信念因 Wiener 的一个基于 Tauber 定理的素数定理证明而受到动摇。尽管如此，Wiener 的证明最终仍依赖于黎曼 zeta 函数在直线 $\operatorname{Re}(s) = 1$ 上的性质，因此不可避免地使用了复分析。

　　 1948 年 3 月，Atle Selberg 使用 “初等方法” 建立了以下渐近公式： $$ \vartheta(x) \log\left(x\right) + \sum_{p \leq x} \log\left(p\right) \, \vartheta\left(\frac{x}{p}\right) = 2x \log\left(x\right) + O(x)~ $$ 其中， $$ \vartheta(x) = \sum_{p \leq x} \log\left(p\right) ~ $$ 对所有素数 $p$ 成立 \(^\text{[11]}\)。

　　 到了同年 7 月，Selberg 与 Paul Erdős\(^\text{[12]}\) 各自独立地基于 Selberg 的这个渐近公式，得出了素数定理的初等证明 \(^\text{[9][26]}\)。这些证明有效地终结了 “PNT 是深奥定理” 这一观点，并表明所谓 “初等” 方法的威力远超先前的认知。 关于素数定理初等证明的历史，包括 Erdős–Selberg 关于优先权的争议，可参阅 Dorian Goldfeld 的一篇文章 \(^\text{[9]}\)。

　　 关于 Erdős 和 Selberg 所得结果的意义，存在一定争议。在数论中，“初等证明” 的概念没有严格且广泛接受的定义，因此他们的证明在何种意义上 “初等”，并不明确。虽然他们的证明不依赖复分析，但实际上在技术上比素数定理的标准证明更为复杂。

　　 一种可能的 “初等证明” 定义是：“可以在一阶 Peano 算术中完成的证明。” 确实存在某些数论命题（例如 Paris–Harrington 定理）只能在二阶系统中证明而不能在一阶中证明，但这类命题至今仍较为少见。

　　 Erdős 和 Selberg 的证明确实可以在 Peano 算术（PA）中形式化。1994 年，Charalambos Cornaros 和 Costas Dimitracopoulos 证明他们的证明可以在 非常弱的 PA 片段——即 $\mathsf{I\Delta_0 + exp}$ 中完成形式化 \(^\text{[27]}\)。然而，这并不能说明标准的素数定理证明是否也可以在 PA 中形式化。

　　 一种更近期的 “初等” 证明：动力系统方法

　　 最近，Florian Richter 给出了一个基于遍历理论的素数定理 “初等” 证明 \(^\text{[28]}\)。在该证明中，素数定理被转化为一个等价形式：Liouville 函数的 Cesàro 和趋于 0。

　　 Liouville 函数定义为：$(-1)^{\omega(n)}$ 其中 $\omega(n)$ 表示正整数 $n$ 的质因数个数（带重数计数）。Bergelson 和 Richter（2022）随后通过一个遍历定理给出该形式的素数定理的证明：

　　 设 $X$ 为紧致度量空间，$T: X \to X$ 为连续自映，$\mu$ 为一个 $T$-不变的 Borel 概率测度，且 $T$ 在该测度下是唯一遍历的。则对于任意连续函数 $f \in C(X)$，都有： $$ \frac{1}{N} \sum_{n=1}^N f(T^{\omega(n)}x) \longrightarrow \int_X f\,d\mu, \quad \forall x \in X.~ $$ 这个遍历定理还可用于对其他与素数定理相关的定理（如 Pillai–Selberg 定理 和 Erdős–Delange 定理）给出 “软证明”（即依赖更少技术细节、更结构性的证明）。

7. 计算机验证

　　 2005 年，Avigad 等人使用 Isabelle 定理证明器，构造出了一个基于 Erdős–Selberg 证明的素数定理变体，并实现了机器验证 \(^\text{[29]}\)。这是第一个被机器形式化验证的素数定理证明。Avigad 之所以选择形式化 Erdős–Selberg 的 “初等” 证明而不是解析证明，是因为当时 Isabelle 的库虽然已经能够处理极限、导数和超越函数等概念，但几乎没有关于积分的理论可供使用 \(^\text{[29]: 19 }\)。

　　 2009 年，John Harrison 使用 HOL Light 定理证明器形式化了一个依赖复分析的素数定理证明 \(^\text{[30]}\)。他开发了所需的分析工具，包括 Cauchy 积分公式，最终能够形式化一个 “直接、现代且优雅的证明，而非更为繁琐的 ‘初等’ Erdős–Selberg 证明”。

8. 算术级数中的素数定理

　　 设 $\pi_{d,a}(x)$ 表示小于 $x$ 的、形如 $a, a + d, a + 2d, a + 3d, \ldots$ 的算术级数中素数的个数。Dirichlet 与 Legendre 曾猜想，de la Vallée Poussin 证明了如下结论：若 $a$ 与 $d$ 互素，则 $$ \pi\_{d,a}(x) \sim \frac{\operatorname{Li}(x)}{\varphi(d)} ~ $$ 其中 $\varphi$ 是欧拉函数。

　　 换句话说，所有与 $d$ 互素的剩余类 $[a]$ 模 $d$ 下的素数是均匀分布的。这一结果比 Dirichlet 关于算术级数中素数的定理更强（后者仅保证每个类中有无限多个素数），并可通过类似 Newman 所用的方法证明素数定理 \(^\text{[31]}\)。

　　 Siegel–Walfisz 定理提供了素数在同余类中分布的良好估计。Bennett 等人 \(^\text{[32]}\) 给出了带显式常数 $A$ 与 $B$ 的以下估计（定理 1.3）：令 $d \geq 3$ 是整数，$a$ 为与 $d$ 互素的整数，则存在正数 $A$ 与 $B$，使得： $$ \left|\pi_{d,a}(x) - \frac{\operatorname{Li}(x)}{\varphi(d)}\right| < \frac{A\, x}{(\log x)^2} \quad \text{对所有 } x \geq B,~ $$ 其中常数 $A$ 的取值为： $$ A = \frac{1}{840} \quad \text{当 } 3 \leq d \leq 10^4 \qquad A = \frac{1}{160} \quad \text{当 } d > 10^4~ $$ 而常数 $B$ 的取值为： $$ B = 8 \cdot 10^9 \quad \text{当 } 3 \leq d \leq 10^5 \qquad B = \exp\left( 0.03\, \sqrt{d}\, (\log d)^3 \right) \quad \text{当 } d > 10^5~ $$

素数竞赛

图
图 3：“函数 π(x; 4, 3) − π(x; 4, 1) 在 n ≤ 30000 范围内的图像”

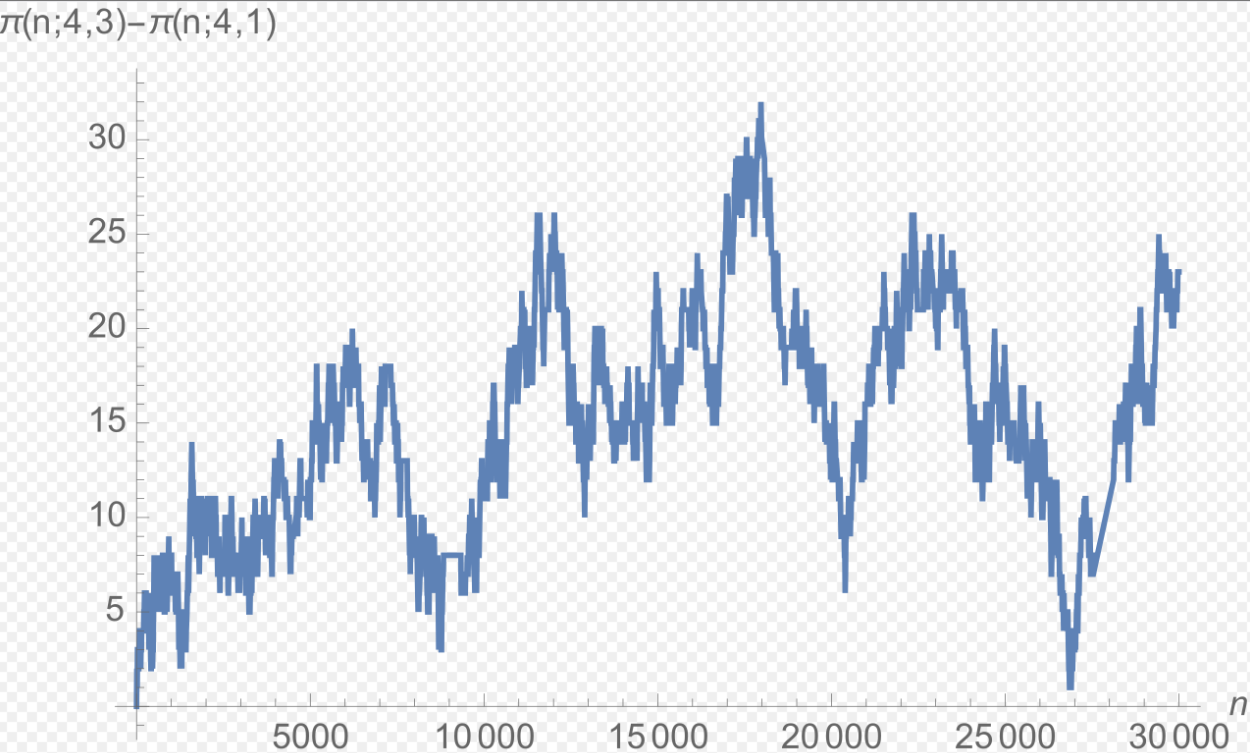
　　 尽管我们有以下结果： $$ \pi_{4,1}(x) \sim \pi_{4,3}(x),~ $$ 也就是说，当 $x$ 趋于无穷时，模 4 同余于 1 和 3 的素数数量是相等的，但从经验上看，满足 $p \equiv 3 \pmod{4}$ 的素数数量更多，在这场 “素数竞赛” 中几乎总是领先；第一次反转出现在 $x = 26861$\(^\text{[33]: 1–2}\) 。然而，Littlewood 在 1914 年证明 \(^\text{[33]: 2}\) ，函数 $$ \pi_{4,1}(x) - \pi_{4,3}(x)~ $$ 存在无穷多个符号变化，也就是说，这场竞赛的领先者会无限次地交替变化。这种现象，即 $\pi_{4,3}(x)$ 大多数时候领先，被称为切比雪夫偏差。素数竞赛的概念可以推广到更一般的模数情形，成为当前数论研究的一个活跃主题。Pál Turán 曾提出一个问题：对于模数 $c$，如果 $a$ 与 $b$ 与 $c$ 互素，是否 $\pi_{c,a}(x)$ 和 $\pi_{c,b}(x)$ 总会互换领先地位？Granville 和 Martin 对此主题有详尽的介绍与综述 \(^\text{[33]}\)。

图
图 4：“$n < 10000$ 时，以 1、3、7 和 9 结尾的素数数量随 $n$ 增长的变化图”

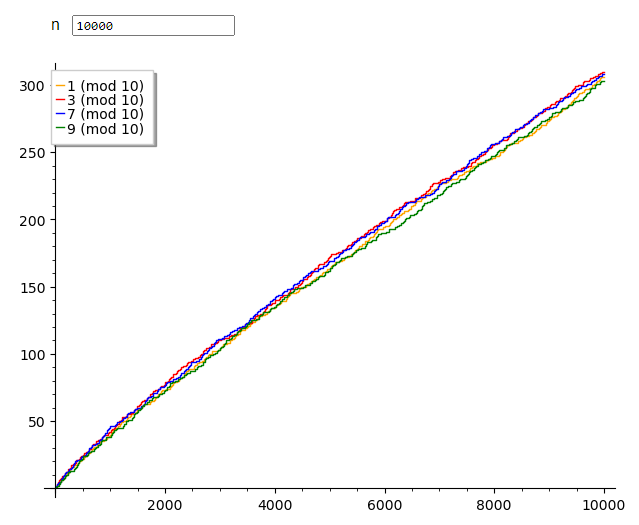
　　 另一个例子是素数个位数字的分布。除了 2 和 5 之外，所有素数的个位只能是 1、3、7 或 9。狄利克雷定理说明，从渐近意义上看，所有素数中有 25% 的个位数字是这四个数中的每一个。然而，实证数据显示，在给定的上限内，个位为 3 或 7 的素数数量往往略多于个位为 1 或 9 的素数（这是切比雪夫偏差的一种体现）\(^\text{[35]}\)。这与模 10 的二次剩余性质有关：1 和 9 是模 10 的二次剩余，而 3 和 7 是模 10 的二次非剩余。

9. 素数计数函数的非渐近界

　　 素数定理是一个渐近结果。根据极限的定义，它对 $\pi(x)$ 给出了一个无效的界：对于所有 $\varepsilon > 0$，存在一个 $S$，使得对于所有 $x > S$，有： $$ (1 - \varepsilon)\frac{x}{\log x} < \pi(x) < (1 + \varepsilon)\frac{x}{\log x}.~ $$ 然而，关于 $\pi(x)$ 存在更好的界，例如皮埃尔·杜萨尔给出的不等式： $$ \frac{x}{\log x}\left(1 + \frac{1}{\log x}\right) < \pi(x) < \frac{x}{\log x}\left(1 + \frac{1}{\log x} + \frac{2.51}{(\log x)^2}\right).~ $$ 其中，第一个不等式对所有 $x \geq 599$ 成立，第二个不等式对 $x \geq 355991$ 成立 \(^\text{[36]}\)。

　　 德拉·瓦莱-普桑的证明还蕴含了如下界：对于每个 $\varepsilon > 0$，存在一个 $S$，使得对于所有 $x > S$，有： $$ \frac{x}{\log x - (1 - \varepsilon)} < \pi(x) < \frac{x}{\log x - (1 + \varepsilon)}.~ $$ 令 $\varepsilon = 3$ 可得到一个较弱但有时有用的界，对所有 $x \geq 55$ 成立 \(^\text{[37]}\)： $$ \frac{x}{\log x + 2} < \pi(x) < \frac{x}{\log x - 4}.~ $$ 在皮埃尔·杜萨尔的博士论文中，存在此类不等式的更强版本，适用于更大的 x。后来在 2010 年，Dusart 证明了以下结论 \(^\text{[38]}\)： $$ \begin{aligned} \frac{x}{\log x - 1} &< \pi(x) &&\text{对于 } x \geq 5393, \\ \pi(x) &< \frac{x}{\log x - 1.1} &&\text{对于 } x \geq 60184. \end{aligned}~ $$

10. 第 n 个素数的近似公式

　　 由素数定理可得，第 n 个素数（记作 pₙ）的一个渐近表达式为： $$ p_n \sim n \log n^\text{[39]}~ $$ 更精确的近似由 Cesàro 在 1894 年提出 \(^\text{[40]}\)： $$ p_n = n B_2(\log n),~ $$ 其中 $$ B_2(x) = x + \log x - 1 + \frac{\log x - 2}{x} - \frac{(\log x)^2 - 6\log x + 11}{2x^2} + o\left(\frac{1}{x^2}\right).~ $$ 仍以第 2×10¹⁷ 个素数 8512677386048191063 为例，假设尾项误差为零，计算得估计值为 8512681315554715386；前五位数字吻合，相对误差约为百万分之 0.46。Cipolla（1902 年）\(^\text{[41][42]}\) 证明上述表达式是一个无限级数的前导项，该级数可以截断到任意次数，其通式为： $$ B_k(x) = x + \log x - 1 - \sum_{i=1}^{k} (-1)^i \frac{P_i(\log x)}{i x^i} + O\left(\frac{(\log x)^{k+1}}{x^{k+1}}\right),~ $$ 其中每个 Pᵢ 是次数为 i 的首一多项式。具体地：$P_1(y) = y - 2$,$P_2(y) = y^2 - 6y + 11$,$P_3(y) = y^3 - \frac{21}{2}y^2 + 42y + \frac{131}{2}$ 等等 \(^\text{[42]}\)。

　　 罗斯塞尔定理 \(^\text{[37]}\) 指出： $$ p_n > n \log n.~ $$ Dusart（1999）\(^\text{[43]}\) 在 Cesàro/Cipolla 近似公式的基础上，通过调整最低阶常数项，给出了更紧的界。令 $B_k(x; C)$ 表示将上述 $B_k(x)$ 中最低阶常数项替换为参数 $C$ 后的函数。

　　 有如下不等式：

　　 对于 $n \geq 2$，有： $$ p_n > n B_0(\log n;\, 1)~ $$ 对于 $n \geq 39017$，有： $$ p_n < n B_0(\log n;\, 0.9484)~ $$ 其中： $$ B_0(x; C) = x + \log x - C~ $$ 对于 $n \geq 2$，有： $$ p_n > n B_1(\log n;\, 2.25)~ $$ 对于 $n \geq 27076$，有： $$ p_n < n B_1(\log n;\, 1.8)~ $$ 其中： $$ B_1(x; C) = x + \log x - 1 + \frac{\log x - C}{x}~ $$ 如果适当放宽参数 $C$，可以将上界推广到更小的 $n$。例如，对于 $n \geq 20$，有：$p_n < n B_1(\log n;\, 0.5)^\text{[44]}$Axler（2019）\(^\text{[44]}\) 进一步推广到了二阶表达式，得到了更高精度的上下界：

　　 对于 \( n \geq 2 \)，有： $$ p_n > n B_2(\log n;\, 11.321)~ $$ 对于 $n \geq 46,\!254,\!381$，有： $$ p_n < n B_2(\log n;\, 10.667)~ $$ 其中： $$ B_2(x; C) = x + \log x - 1 + \frac{\log x - 2}{x} - \frac{(\log x)^2 - 6 \log x + C}{2 x^2}~ $$ 同样地，如果放宽参数 C，例如令 $C = 0$，则当 $n \geq 3468$ 时仍有：$p_n < n B_2(\log n; 0)$

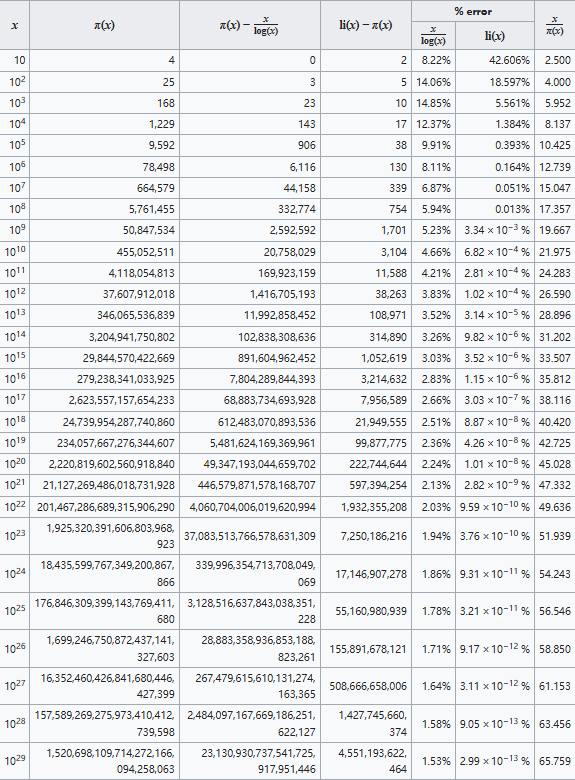
11. π(x)、x / log x 与 li(x) 对照表

　　 本表比较了素数计数函数 $\pi(x)$ 的精确值与两个近似值 $x/\log x$ 和 $\operatorname{li}(x)$。其中：“近似差值” 列已四舍五入为最接近的整数；“% 误差” 列则基于未四舍五入的近似值计算得出；最后一列 $x/\pi(x)$ 表示 x 以下的素数平均间距。

图
图 5

　　 $\pi(10^{24})$ 的数值最初是在假设黎曼猜想成立的前提下计算出来的；此后，该数值已被无条件地验证。\(^\text{[45][46]}\)

12. 有限域上不可约多项式的类似素数定理

　　 存在一个关于不可约多项式在有限域中 “分布” 的素数定理类比，其形式与经典素数定理惊人地相似。为了精确定义，设 $F = \mathrm{GF}(q)$ 是具有 $q$ 个元素的有限域，其中 $q$ 是一个固定的素数幂。令 $N_n$ 表示所有次数为 $n$ 的一元首一（首项系数为 1）不可约多项式的个数。换句话说，我们关注的是那些无法写成低次多项式乘积的一元首一多项式。在这个背景下，这些不可约多项式扮演了 “素数” 的角色，因为其他所有的一元首一多项式都可以由它们构造而成。

　　 可以证明如下的类比关系： $$ N_n \sim \frac{q^n}{n}.~ $$ 若作变量替换 $x = q^n$，则右边可写作： $$ \frac{x}{\log_q x},~ $$ 这使得类比关系更加清晰。注意，次数为 $n$ 的一元首一多项式的总数正好为 $q^n$（包括可约和不可约的情况），因此我们也可以这样表述：从中随机选取一个一元首一多项式，其为不可约的概率大约为 $\frac{1}{n}$。

　　 甚至还可以证明黎曼猜想的一个类比形式，即： $$ N_n = \frac{q^n}{n} + O\left(\frac{q^{\frac{n}{2}}}{n}\right).~ $$ 与经典实数域中的素数定理相比，这些结论的证明要简单得多，它们可以通过一个简短的组合论推导得到，其要点如下：

　　 有限域 $F$ 的次数为 $n$ 的扩域中的每一个元素，都是某个次数为 $d \mid n$ 的不可约多项式的根。通过两种不同方式计数这些根，可得到恒等式： $$ q^n = \sum_{d \mid n} d N_d,~ $$ 其中求和范围是所有 $n$ 的正约数 $d$。应用莫比乌斯反演公式，可以推出： $$ N_n = \frac{1}{n} \sum_{d \mid n} \mu\left(\frac{n}{d}\right) q^d,~ $$ 其中 $\mu(k)$ 是莫比乌斯函数。（这个公式早在高斯时代就已为人所知。）主项出现在 $d = n$ 时，而其余项也可以较容易地估计上界。类黎曼猜想形式的误差估计依赖于这样的事实：$n$ 的最大真约数不超过 $\frac{n}{2}$。

13. 参见

14. 参考文献

  1. Hadamard, Jacques（1896），《关于ζ(s)函数零点的分布及其算术后果》，载《法国数学会会报》，第 24 卷，法国数学会，第 199–220 页，原文已于 2024 年 9 月 10 日存档。
  2. de la Vallée Poussin, Charles-Jean（1896），《关于素数理论的分析性研究》，载《布鲁塞尔科学学会会报》，第 20B、21B 卷，比利时皇家科学院印刷部，第 183–256 页、第 281–352 页、第 363–397 页、第 351–368 页。
  3. Hoffman, Paul（1998），《只爱数字的人》，纽约：海波利恩出版社，第 227 页，ISBN 978-0-7868-8406-3，数学评论号：MR 1666054。
  4. 《素数奇趣！：8512677386048191063》，素数奇趣网站，田纳西大学马丁分校，2011 年 10 月 9 日。
  5. Apostol, Tom M.（1976），《解析数论导论》，本科数学教材系列，第一版，施普林格出版社（Springer），doi:10.1007/978-1-4757-5579-4，ISBN 978-1-4757-5579-4。
  6. Gauss, C. F.（1863），《高斯全集》第 2 卷，第一版，哥廷根：图布纳出版社（Teubner），第 444–447 页。
  7. Costa Pereira, N.（1985 年 8 月–9 月），《切比雪夫定理的一个简短证明》，载《美国数学月刊》，第 92 卷第 7 期，第 494–495 页，doi:10.2307/2322510，JSTOR 编号：2322510。
  8. Nair, M.（1982 年 2 月），《关于素数的切比雪夫型不等式》，载《美国数学月刊》（American Mathematical Monthly），第 89 卷第 2 期，第 126–129 页，doi:10.2307/2320934，JSTOR 编号：2320934。
  9. Goldfeld, Dorian（2004），《素数定理初等证明的历史视角》，见 Chudnovsky, David；Chudnovsky, Gregory；Nathanson, Melvyn 编，《数论》（Number theory，2003 年纽约会议文集），纽约：Springer-Verlag，第 179–192 页，doi:10.1007/978-1-4419-9060-0_10，ISBN 978-0-387-40655-8，数学评论号：MR 2044518。
  10. Ingham, A. E.（1990），《素数的分布》，剑桥大学出版社，第 2–5 页，ISBN 978-0-521-39789-6。
  11. Selberg, Atle（1949），“素数定理的一个初等证明”，载《数学年刊》，第 50 卷第 2 期，第 305–313 页，doi:10.2307/1969455，JSTOR 编号：1969455，数学评论号：MR 0029410，S2CID：124153092。
  12. Erdős, Paul（1949 年 7 月 1 日），“一种初等数论的新方法，它导出了素数定理的初等证明”（PDF），载《美国国家科学院院刊》，第 35 卷第 7 期，美国国家科学院出版，第 374–384 页，Bibcode: 1949PNAS...35..374E，doi:10.1073/pnas.35.7.374，PMC 编号：1063042，PMID 编号：16588909。
  13. Newman, Donald J.（1980），“素数定理的一个简单解析证明”，载《美国数学月刊》，第 87 卷第 9 期，第 693–696 页，doi:10.2307/2321853，JSTOR 编号：2321853，数学评论号：MR 0602825。
  14. Zagier, Don（1997），“Newman 版素数定理简明证明”，载《美国数学月刊》，第 104 卷第 8 期，第 705–708 页，doi:10.2307/2975232，JSTOR 编号：2975232，数学评论号：MR 1476753。
  15. Tao, Terence（2014 年 12 月 10 日），“254A，第 2 讲笔记：复分析的乘法数论”，发表于 Terence Tao 的博客。
  16. Edwards, Harold M.（2001），《黎曼ζ函数》，Courier Dover 出版社，ISBN 978-0-486-41740-0。
  17. de la Vallée Poussin, Charles-Jean（1899），“关于黎曼ζ(s)函数及小于给定上限的素数个数”，载《比利时皇家科学院获奖论文集》，第 59 卷，比利时皇家科学院印刷部，第 1–74 页。
  18. Kevin Ford（2002），“Vinogradov 积分与黎曼ζ函数的界”（PDF），载《伦敦数学会会刊》，第 85 卷第 3 期，第 565–633 页，arXiv:1910.08209，doi:10.1112/S0024611502013655，S2CID 编号：121144007。
  19. Timothy Trudgian（2016 年 2 月），“素数定理误差项的更新”，载《拉马努金杂志》，第 39 卷第 2 期，第 225–234 页，arXiv:1401.2689，doi:10.1007/s11139-014-9656-6，S2CID 编号：11013503。
  20. von Koch, Helge（1901），“关于素数的分布”（法文），载《数学学报》，第 24 卷第 1 期，第 159–182 页，doi:10.1007/BF02403071，数学评论号：MR 1554926，S2CID 编号：119914826。
  21. Schoenfeld, Lowell（1976），“对切比雪夫函数 ϑ(x) 与 ψ(x) 的更精确界限（二）”，载《数学计算》，第 30 卷第 134 期，第 337–360 页，doi:10.2307/2005976，JSTOR 编号：2005976，数学评论号：MR 0457374。
  22. Jørgensen, Bent；Martínez, José Raúl；Tsao, Min（1994），“方差函数的渐近行为”，载《斯堪的纳维亚统计学杂志》，第 21 卷第 3 期，第 223–243 页，JSTOR 编号：4616314，数学评论号：MR 1292637。
  23. Littlewood, J.E.（1914），“关于素数的分布”，载《法国科学院报告》，第 158 卷，第 1869–1872 页，数学文摘编号：JFM 45.0305.01。
  24. Hardy, G. H.；Littlewood, J. E.（1916），“关于黎曼ζ函数理论与素数分布理论的若干贡献”，载《数学学报》，第 41 卷，第 119–196 页，doi:10.1007/BF02422942。
  25. Davenport, Harold；Montgomery, Hugh L.（2000）《乘法数论》，《数学研究生教材》系列第 74 卷（修订第三版），Springer 出版社，ISBN：978-0-387-95097-6。
  26. Baas, Nils A.；Skau, Christian F.（2008），“数之主——阿特勒·塞尔伯格：他的生平与数学”，载《美国数学会通报》（Bulletin of the American Mathematical Society），第 45 卷第 4 期，第 617–649 页，doi:10.1090/S0273-0979-08-01223-8，数学评论号：MR 2434348。
  27. Cornaros, Charalambos；Dimitracopoulos, Costas（1994），“素数定理与皮亚诺算术的若干片段”，载《数学逻辑档案》，第 33 卷第 4 期，第 265–281 页，doi:10.1007/BF01270626，数学评论号：MR 1294272，S2CID：29171246。原文 PDF 存档于 2011 年 7 月 21 日。
  28. Bergelson, V.；Richter, F. K.（2022），“素数定理的动力学推广及加法与乘法半群作用的相异性”，载《杜克数学期刊》，第 171 卷第 15 期，第 3133–3200 页。
  29. Avigad, Jeremy；Donnelly, Kevin；Gray, David；Raff, Paul（2008），“素数定理的形式化验证证明”，载《ACM 计算逻辑学报》，第 9 卷第 1 期，文章编号 2，arXiv\:cs/0509025，doi:10.1145/1297658.1297660，数学评论号：MR 2371488，S2CID：7720253。
  30. Harrison, John（2009），“对素数定理解析证明的形式化”，载《自动推理杂志》（，第 43 卷第 3 期，第 243–261 页，CiteSeerX：10.1.1.646.9725，doi:10.1007/s10817-009-9145-6，数学评论号：MR 2544285，S2CID：8032103。
  31. Soprounov, Ivan（1998），“关于算术级数中的素数定理的一个简短证明”，俄亥俄州：克利夫兰州立大学。CiteSeerX: 10.1.1.179.460。
  32. Bennett, Michael A.；Martin, Greg；O'Bryant, Kevin；Rechnitzer, Andrew（2018），“算术级数中素数的显式界”，《伊利诺伊数学杂志》，第 62 卷第 1–4 期，第 427–532 页，arXiv:1802.00085，doi:10.1215/ijm/1552442669，S2CID: 119647640。
  33. Granville, Andrew；Martin, Greg（2006），“素数竞赛”，《美国数学月刊》，第 113 卷第 1 期，第 1–33 页，doi:10.2307/27641834，JSTOR: 27641834，数学评论号：MR 2202918。 [PDF 原文标题：Prime number races]
  34. Guy, Richard K.（2004）《数论中的未解问题》，第 3 版，Springer-Verlag 出版社，第 A4 节，第 13–15 页，ISBN: 978-0-387-20860-2，Zbl: 1058.11001。 本书采用的记号是 π(x; a, c)，而本文使用的是 π_c,a(x)，表示模 c 同余于 a 的素数个数。
  35. Lemke Oliver, Robert J.；Soundararajan, Kannan（2016 年 8 月 2 日），“连续素数分布中的意外偏差”，《美国国家科学院院刊》，第 113 卷第 31 期，E4446–E4454 页，arXiv:1603.03720，Bibcode: 2016PNAS..113E4446L，doi:10.1073/pnas.1605366113，ISSN: 0027-8424，PMC: 4978288，PMID: 27418603。
  36. Dusart, Pierre（1998 年 5 月 26 日）《关于计数素数个数的函数》，数学系博士论文（法语），法国利摩日大学提供的 PDF 版本。
  37. Rosser, Barkley（1941），“关于素数函数的一些显式界”，《美国数学杂志》，第 63 卷第 1 期，第 211–232 页，doi:10.2307/2371291，JSTOR: 2371291，数学评论号：MR 0003018。
  38. Dusart, Pierre（2010 年 2 月 2 日）。“对某些素数函数的估计，不依赖黎曼假设。” arXiv:1002.0442。
  39. “为什么 $p_n \sim n \ln\left(n\right) $？” 数学 Stack Exchange，检索日期：2024 年 10 月 11 日。
  40. Cesàro, Ernesto（1894）。“关于 Pervouchine 先生的一个经验公式。”《法兰西科学院会议纪要》，第 119 卷，第 848–849 页（法语）。
  41. Cipolla, Michele（1902）。“第 n 个素数的渐近确定” [La determinazione assintotica dell'nimo numero primo]。《那不勒斯数学杂志》，第 8 卷，第 3 期，第 132–166 页（意大利语）。
  42. Arias de Reyna, Juan；Toulisse, Jérémy（2013）。“第 n 个素数的渐近估计。”《波尔多数论杂志》，第 25 卷第 3 期，第 521–555 页，arXiv:1203.5413，doi:10.5802/jtnb.847，数学评论号：MR 3179675，Zbl 1298.11093。
  43. Dusart, Pierre（1999）。“第 k 个素数大于 $k(\log k + \log \log k - 1)$，适用于 $k \geq 2$。”《数学计算》（Mathematics of Computation），第 68 卷第 225 期，第 411–415 页，doi:10.1090/S0025-5718-99-01037-6，数学评论号：MR 1620223。
  44. Axler, Christian（2019）。“关于第 n 个素数的新估计。”《整数序列期刊》，22 卷，编号：19.4.2，arXiv:1706.03651。
  45. “π(1024) 的条件计算。” 作者：Chris K. Caldwell。原始网页已于 2010 年 8 月 4 日归档。检索日期：2010 年 8 月 3 日。
  46. Platt, David（2015）。“通过解析方法计算 π(x)。”《数学计算》，第 84 卷第 293 期，第 1521–1535 页，arXiv:1203.5712，doi:10.1090/S0025-5718-2014-02884-6，数学评论号：MR 3315519，S2CID：119174627。
  47. Chebolu, Sunil；Mináč, Ján（2011 年 12 月）。“利用容斥原理统计有限域上的不可约多项式。”《数学杂志》，第 84 卷第 5 期，第 369–371 页，arXiv:1001.0409，doi:10.4169/math.mag.84.5.369，JSTOR 编号：10.4169/math.mag.84.5.369，S2CID：115181186。

15. 参考文献

16. 外部链接

                     

© 保留一切权利