大数定律（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在概率论中，大数定律是一条数学规律，它指出：在大量相互独立的随机样本中获得的结果的平均值将收敛于真实值（如果这个真实值存在）\(^\text{[1]}\)。更正式地说，大数定律表明：对于一组独立同分布的样本，其样本均值将趋于真实的数学期望。

　　 大数定律的重要性在于，它为某些随机事件的平均值提供了长期稳定的保证 \(^\text{[1][2]}\)。例如，一个赌场在某次轮盘赌中可能会亏损，但在大量旋转后，其收益将趋近于一个可预测的百分比。任何玩家的连胜最终也会被游戏设定所 “拉回”。需要注意的是，大数定律（顾名思义）只在观测次数足够大时才适用。并没有任何原则表明少数几次的观测结果就会接近期望值，或者说某种结果的连发会立即被其他结果 “平衡”（参见赌徒谬误）。

　　 大数定律仅适用于重复试验结果的平均值，并声称这个平均值会收敛到期望值；它并不意味着随着试验次数 $n$ 的增加，结果的总和一定会接近 $n$ 倍的期望值。

　　 在其发展历程中，许多数学家对大数定律进行了不断完善。如今，大数定律被广泛应用于统计学、概率论、经济学以及保险学等多个领域 \(^\text{[3]}\)。

1. 示例

图
图 1：用一次掷单个骰子的特定实验来说明大数定律。随着该实验中掷骰次数的增加，所有结果数值的平均值逐渐趋近于 3.5。尽管在掷骰次数较少时（左侧）每次实验的曲线形状会有明显差异，但当掷骰次数增多时（右侧），这些曲线的形状将会极为相似。

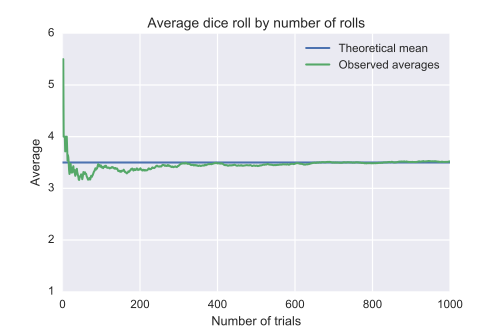
　　 例如，掷一次六面骰子会得到 1、2、3、4、5 或 6 中的一个结果，每个数字出现的概率相等。因此，这次掷骰子的**期望值**是： $$ \frac{1 + 2 + 3 + 4 + 5 + 6}{6} = 3.5~ $$ 根据大数定律，如果掷出大量的六面骰子，这些点数的平均值（有时称为样本均值）将趋近于 3.5，且随着掷骰数量的增加，结果的精确度也会提高。

　　 大数定律还意味着，在一系列伯努利试验中，成功的经验概率会收敛于理论概率。对于伯努利随机变量，其期望值就是成功的理论概率，而 $n$ 个这样的变量的平均值（假设它们是独立同分布（i.i.d.）的）恰好就是相对频率。

图
图 2：这张图说明了相对频率向理论概率收敛的过程。假设从一个袋子中抽取红球的概率是 0.4，抽取黑球的概率是 0.6。左侧图显示的是抽到黑球的相对频率，右侧图显示的是抽到红球的相对频率，二者均基于 10,000 次试验。随着试验次数的增加，相对频率逐渐趋近于各自的理论概率，从而体现了大数定律的作用。

　　 例如，掷一枚公平硬币就是一次伯努利试验。当公平硬币被掷一次时，结果为正面的理论概率是 $\frac{1}{2}$。因此，根据大数定律，在进行 “大量” 掷硬币试验时，正面朝上的比例 “应当” 大约为 $\frac{1}{2}$。特别地，随着掷币次数 $n$ 趋近于无穷，正面朝上的比例将几乎必然地收敛到 $\frac{1}{2}$。

　　 尽管正反面比例趋近于 $\frac{1}{2}$，正反面次数的绝对差值却几乎必然会随着试验次数增加而变大。也就是说，这个差值保持在一个很小的数值的概率会趋近于零。不过，这个差值与试验总次数的比例几乎必然趋近于零。从直觉上说，差值确实在增长，但它的增长速度比总次数慢。

　　 另一个很好地体现大数定律的例子是蒙特卡洛方法。这是一大类依赖重复随机抽样以获得数值结果的计算算法。重复次数越多，得到的近似结果通常也越准确。该方法的重要性主要在于，有时候使用其他方法求解是非常困难甚至不可能的 \(^\text{[4]}\)。

2. 局限性

　　 在某些情况下，从大量试验中获得的结果的平均值可能不会收敛。例如，从柯西分布或某些 帕累托分布（Pareto distribution，α<1）中抽取的 $n$ 个结果的平均值不会随着 $n$ 增大而收敛，其原因在于这些分布具有重尾特性。\(^\text{[5]}\) 柯西分布是一个没有数学期望的分布 \(^\text{[6]}\)，而当帕累托分布的参数 α 小于 1 时，其期望值为无穷大。\(^\text{[7]}\) 生成一个柯西分布的例子的方法之一是：令随机数等于一个在区间 $-90^\circ$ 到 $+90^\circ$ 内均匀分布的角度的正切值。\(^\text{[8]}\) 这个分布的中位数为 0，但其数学期望不存在，并且 $n$ 个此类变量的平均值具有与其中任意一个变量相同的分布。因此，即使 $n$ 趋于无穷大，这个平均值在概率意义上不会收敛到 0 或任何其他值。

　　 此外，如果试验中存在选择性偏差——例如人类的经济或理性行为中常见的偏差——即使增加试验次数，大数定律也无法消除这种偏差，偏差仍然会存在。

3. 历史

图
图 3：扩散现象是大数法则的一个实例。一开始，容器中隔板（品红色线）左侧存在溶质分子，而右侧则没有。移除隔板后，溶质开始扩散，最终填满整个容器。顶部：当只有一个分子时，其运动看起来是完全随机的。中部：当分子数量增加时，虽然仍然存在随机波动，但可以明显看出溶质趋向于更加均匀地填满容器。底部：当溶质分子的数量极其庞大（多到无法看见）时，随机性基本消失：溶质似乎平滑而有规律地从高浓度区域流向低浓度区域。在现实情况下，尽管扩散的本质是随机的，化学家仍可以将其视为一种确定性的宏观现象（参见菲克定律）。

　　 意大利数学家杰罗拉莫·卡尔达诺（Gerolamo Cardano，1501–1576）曾在未加证明的情况下指出，经验统计的准确性随着试验次数的增加而提高。\(^\text{[9][3]}\) 后来，这一观点被正式表述为 “大数法则”。大数法则的一种特殊形式（适用于二元随机变量）最早由雅各布·伯努利证明。\(^\text{[10][3]}\) 他花费了超过 20 年时间，才发展出足够严谨的数学证明，并于 1713 年在其著作《概率术》中发表。他将其称为 “金色定理”，但后世更常称之为 “伯努利定理”。这一定理不应与 “伯努利原理” 混淆，后者是以雅各布的侄子丹尼尔·伯努利的名字命名的。1837 年，西梅翁·德尼·泊松以 “la loi des grands nombres”（法语，意为 “大数法则”）的名称进一步描述了这一原理。\(^\text{[11][12][3]}\) 此后，这一法则在文献中以这两个名称交替出现，但 “law of large numbers”（大数法则）是最常用的名称。

　　 在伯努利和泊松发表其成果之后，其他数学家也对大数法则进行了改进与拓展，其中包括切比雪夫（、马尔可夫、博雷尔、坎特利、柯尔莫哥洛夫和欣钦等人。\(^\text{[3]}\) 马尔可夫证明了在某些较弱的条件下，大数法则仍适用于方差不存在的随机变量；1929 年，欣钦进一步证明，如果一组独立同分布的随机变量具有期望值，那么弱大数法则就成立。\(^\text{[14][15]}\) 这些后续研究发展出了大数法则的两个主要形式：一种称为 “弱大数法则”，另一种称为 “强大数法则”，分别对应于样本均值趋近于期望值的两种不同收敛方式；特别地，如下文所解释的，强大数法则蕴含弱大数法则。\(^\text{[14]}\)

4. 形式

　　 大数法则有两个不同的版本，称为强大数法则和弱大数法则 \(^\text{[16][1]}\)。以下是它们在如下情形下的表述：设 $X_1, X_2, \dots$ 是一个无限序列的独立同分布（i.i.d.）的勒贝格可积随机变量，其期望满足： $$ \mathbb{E}(X_1) = \mathbb{E}(X_2) = \cdots = \mu~ $$ 这两个版本都断言样本平均值： $$ \overline{X}_n = \frac{1}{n}(X_1 + \cdots + X_n)~ $$ 收敛于期望值： $$ \overline{X}_n \to \mu \quad \text{当 } n \to \infty~ $$ （其中 “勒贝格可积” 意味着 $\mathbb{E}(X_j)$ 按照勒贝格积分存在且有限；这并不意味着相关的概率测度对勒贝格测度绝对连续。）

　　 入门级的概率教材通常还额外假设每个随机变量具有相同的有限方差，即： $$ \operatorname{Var}(X_i) = \sigma^2 \quad \text{对所有 } i~ $$ 并且各随机变量之间不相关。在这种情况下，$n$ 个随机变量的样本均值的方差为： $$ \operatorname{Var}(\overline{X}_n) = \operatorname{Var}\left(\frac{1}{n}(X_1 + \cdots + X_n)\right) = \frac{1}{n^2} \operatorname{Var}(X_1 + \cdots + X_n) = \frac{n\sigma^2}{n^2} = \frac{\sigma^2}{n}~ $$ 这个公式可用于简化和缩短相关证明。但这种有限方差的假设并非必要。即使存在较大或无限的方差，只是会导致收敛速度变慢，大数法则依然成立 \(^\text{[17]}\)。

　　 随机变量的相互独立性也可以被两两独立性 \(^\text{[18]}\) 或可交换性 \(^\text{[19]}\) 所取代，两种形式的大数法则仍然适用。

　　 强大数法则和弱大数法则之间的区别在于所主张的收敛方式不同。关于这些收敛方式的解释，可参见 “随机变量的收敛性” 相关内容。

弱大数法则

图
图 4：模拟演示大数法则：每一帧中都会抛掷一枚硬币，其一面为红色，另一面为蓝色，并在对应的柱状图列中添加一个点。饼图显示当前红色与蓝色的比例。可以看到，虽然在初期比例波动较大，但随着试验次数的增加，比例逐渐趋近于 50\%。

　　 弱大数法则（也称为欣钦法则，Khinchin's law）指出：如果一组样本是从具有有限期望值的随机变量中独立同分布（i.i.d.）地抽取的，那么其样本均值将按概率收敛于该期望值： $$ \overline{X}_n \xrightarrow{P} \mu \quad \text{当 } n \to \infty~ $$ 也就是说，对于任意正数 ε，有： $$ \lim_{n \to \infty} \Pr\left(|\overline{X}_n - \mu| < \varepsilon\right) = 1~ $$ 解释这个结果：弱大数法则意味着，对于任意非零的容差（$\varepsilon$），无论多小，只要样本量足够大，样本均值以极高的概率落在该容差范围内，也就是说，会非常接近于期望值。

　　 正如前面提到的，弱大数法则适用于 i.i.d. 随机变量的情形，但它也适用于其他一些情况。例如：序列中的每个随机变量的方差可以不同，只要它们的期望值保持不变。如果这些方差是有界的，那么该法则依然成立，这一点早在 1867 年就被切比雪夫证明过。

　　 （如果期望值在序列中发生变化，我们可以将法则应用于每个变量与其期望值之间的平均偏差。此时法则表明，这一偏差按概率收敛于零。）事实上，只要前 $n$ 项的样本均值的方差在 $n \to \infty$ 时趋于零，切比雪夫的证明就成立 \(^\text{[15]}\)。例如，假设该序列中的每个随机变量都服从均值为 0、方差为 $2n/ \log\left(n+1\right) $ 的高斯分布（正态分布）。虽然方差不是有界的，但每一步的样本均值仍服从正态分布（因为是正态变量的平均值）。此时，总和的方差是各项方差之和，渐近等于 $n^2 / \log n$，因此样本均值的方差渐近等于 $1 / \log n$，并趋于零。还有一些例子表明，即使期望值不存在，弱大数法则也可能适用。

强大数法则

　　 强大数法则（也称为柯尔莫哥洛夫法则）指出：样本平均值几乎必然收敛于期望值[21]： $$ \overline{X}_n \xrightarrow{\text{a.s.}} \mu \quad \text{当 } n \to \infty~ $$ 也就是说： $$ \Pr\left(\lim_{n \to \infty} \overline{X}_n = \mu\right) = 1~ $$ 这意味着，当试验次数 $n$ 趋于无穷时，样本平均值收敛于期望值的概率为 1。相比弱大数法则，强大数法则的现代证明更为复杂，通常依赖于构造适当的子序列来完成证明 \(^\text{[17]}\)。

　　 强大数法则本身可以看作是遍历定理的一个特例。这种观点为随机变量的期望值（在勒贝格积分意义下）提供了直观解释，即 “长期平均” 的含义。

　　 此法则被称为 “强” 大数法则，是因为几乎处处收敛意味着依概率收敛；也就是说，强收敛蕴含弱收敛。然而，弱大数法则在某些强大数法则不适用的情形下仍然成立，这种情况下的收敛是仅仅弱的。参见 “强弱大数法则的区别”。

　　 强大数法则适用于具有期望值的独立同分布随机变量（如同弱大数法则）。这是由柯尔莫哥洛夫在 1930 年首次证明的。他在 1933 年进一步证明：如果一组变量是独立同分布的，那么要使平均值几乎处处收敛于某个数（这可以视为强大数法则的另一种表述），那么这些变量必须具有期望值（一旦期望存在，平均值就会几乎处处收敛于它）\(^\text{[22]}\)。

　　 如果各项是独立但不同分布的，那么仍然有： $$ \overline{X}_n - \operatorname{E}[\overline{X}_n] \xrightarrow{\text{a.s.}} 0~ $$ 前提是每个 $X_k$ 都具有有限的二阶矩，并且满足条件： $$ \sum_{k=1}^{\infty} \frac{1}{k^2} \operatorname{Var}[X_k] < \infty~ $$ 该陈述被称为柯尔莫哥洛夫强大数法则，可参见 Sen & Singer (1993, 定理 2.3.10)。

弱大数法则与强大数法则的区别

　　 弱大数法则表明，对于某个足够大的 $n$，样本平均值 $\overline{X}_n$ 很有可能接近期望值 $\mu$\(^\text{[23]}\)。因此，它允许存在无限多次 $|\overline{X}_n - \mu| > \varepsilon$ 的情形，尽管这种偏离会随着 $n$ 增大变得越来越罕见。（但不必然意味着对所有 $n$，都有 $|\overline{X}_n - \mu| \ne 0$）

　　 而强大数法则则表明，这种情况几乎肯定不会发生。也就是说，对于任意 $\varepsilon > 0$，几乎处处地存在某个足够大的 $N$，使得当 $n > N$ 时，不等式： $$ |\overline{X}_n - \mu| < \varepsilon~ $$ 恒成立 \(^\text{[24]}\)。换句话说，从某个时刻开始，样本平均值将一直保持在期望值 $\mu$ 的 $\varepsilon$ 邻域内，几乎必然如此。这正是强大数法则的收敛更强的体现。

　　 以下情况中，强大数法则不成立，但弱大数法则成立 \(^\text{[25][26]}\)：

  1. 设 $X$ 是一个参数为 1 的指数分布随机变量。随机变量 $\frac{ \sin\left(X\right) e^{X}}{X}$ 根据勒贝格积分的定义是没有期望值的，但如果采用条件收敛的方式，并将该积分解释为狄利克雷积分，即一个非正常的黎曼积分，我们可以得到： $$ \mathbb{E}\left(\frac{ \sin\left(X\right) e^{X}}{X}\right) = \int_{x=0}^{\infty} \frac{ \sin\left(x\right) e^{x}}{x} e^{-x} \, dx = \frac{\pi}{2}~ $$ 这说明虽然按照严格的勒贝格积分定义期望值不存在，但在较弱条件下（例如弱大数法则适用的情境中）仍可得出某种 “期望” 意义下的收敛结果。
  2. 设 $X$ 是一个以 0.5 为成功概率的几何分布随机变量。随机变量 $\frac{2^{X}(-1)^{X}}{X}$ 在常规意义下没有期望值，因为对应的无穷级数不是绝对收敛的。但如果使用条件收敛的方式，我们可以得到： $$ \mathbb{E}\left(\frac{2^{X}(-1)^{X}}{X}\right) = \sum_{x=1}^{\infty} \frac{2^{x}(-1)^{x}}{x} \cdot 2^{-x} = - \ln\left(2\right) ~ $$
  3. 另外，若某个随机变量的累积分布函数为： $$ \begin{cases} 1 - F(x) = \dfrac{e}{2x \ln\left(x\right) }, & x \geq e \\ F(x) = \dfrac{e}{-2x \ln\left(-x\right) }, & x \leq -e \end{cases}~ $$ 那么该随机变量没有期望值，但弱大数法则仍然成立【27】【28】。
  4. 设 $X_k$ 是取值为 $\pm \sqrt{k/\log \log \log k}$ 的随机变量（从足够大的 $k$ 开始，以确保分母为正），且各取值的概率均为 $\frac{1}{2}$【22】。那么 $X_k$ 的方差为：$\frac{k}{\log \log \log k}$ 由于对 Kolmogorov 强大数法则来说，其判据中的部分和在 $k = n$ 时的渐进行为是：$\frac{\log n}{\log \log \log n}$ 这是无界的，因此 Kolmogorov 的强大数法则不适用。 如果我们将这些随机变量替换为具有相同方差的高斯变量（即均值为 0、方差为 $\frac{k}{\log \log \log k}$ 的正态分布），那么在任意时刻的平均值也将服从正态分布。此时其标准差的渐进行为为：$\frac{1}{\sqrt{2 \log \log \log n}}$ 随着 $n$ 增大，平均值的分布宽度趋于 0，但对于给定的 $\varepsilon$，总存在一个不趋于 0 的概率，表明在第 $n$ 次试验之后的某一时刻，平均值将重新达到 $\varepsilon$。由于分布宽度不为 0，因此存在一个正的下界 $p(\varepsilon)$，即在 $n$ 次试验后，平均值达到 $\varepsilon$ 的概率至少为 $p(\varepsilon)$。平均值在某个依赖于 $n$ 的 $m$ 次试验前达到 $\varepsilon$ 的概率至少为 $\frac{p(\varepsilon)}{2}$，而即使在 $m$ 次试验之后，平均值仍有至少 $p(\varepsilon)$ 的概率达到 $\varepsilon$。这似乎说明 $p(\varepsilon) = 1$，即平均值将以概率 1 无穷次地达到 $\varepsilon$。

一致大数法则

　　 一致大数法则是对经典大数法则的推广，适用于一类估计量的集合，其收敛在该集合上是一致的，因此得名 “一致大数法则”。

　　 设 $f(x, \theta)$ 是在 $\theta \in \Theta$ 上定义的某个函数，并且在 $\theta$ 上是连续的。那么对于任意固定的 $\theta$，序列 $\{f(X_1, \theta), f(X_2, \theta), \dots\}$ 将是一组独立同分布的随机变量，其样本均值按概率收敛于 $\mathbf{E}[f(X, \theta)]$。这称为对每个 $\theta$ 的逐点收敛。

　　 而一致大数法则给出了收敛在整个 $\theta$ 空间内一致成立的条件。具体来说，如果满足以下条件 \(^\text{[29][30]}\)：

  1. $\Theta$ 是紧集；
  2. $f(x, \theta)$ 对于几乎所有 $x$ 在每个 $\theta \in \Theta$ 处连续，且对每个 $\theta$ 来说是 $x$ 的可测函数；
  3. 存在一个主导函数 $d(x)$，使得 $\mathbf{E}[d(X)] < \infty$； 并且对所有 $\theta \in \Theta$，都有： $$ \| f(x, \theta) \| \leq d(x)~ $$

　　 那么 $\mathbb{E}[f(X, \theta)]$ 在 $\theta$ 上是连续的，且有： $$ \sup_{\theta \in \Theta} \left\| \frac{1}{n} \sum_{i=1}^{n} f(X_i, \theta) - \mathbb{E}[f(X, \theta)] \right\| \xrightarrow{P} 0~ $$ 即，样本均值对期望的偏差在整个 $\Theta$ 上按概率一致收敛于 0。这个结果在推导极值估计量的相合性时非常有用。

伯雷尔大数法则

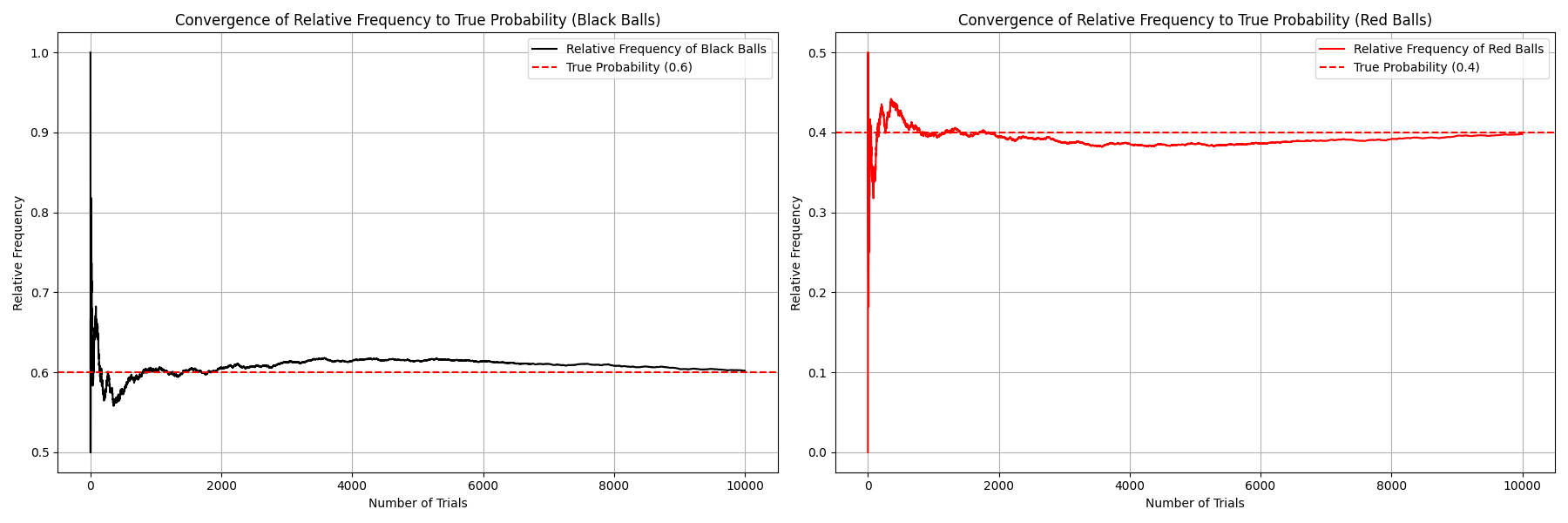
　　 伯雷尔大数法则（以法国数学家埃米尔·伯雷尔 Émile Borel 命名）指出：如果一个实验在相同条件下独立重复进行大量次，那么某一特定事件发生的频率比例将趋近于该事件在单次试验中发生的概率；重复次数越多，这种近似就越准确。

　　 更精确地说，设 $E$ 表示某个事件，$p$ 是该事件在一次试验中发生的概率，$N_n(E)$ 表示事件 $E$ 在前 $n$ 次试验中发生的次数，则有概率为 1（即 “几乎必然”）地成立： $$ \frac{N_n(E)}{n} \to p \quad \text{当} \quad n \to \infty.~ $$ 这个定理为我们日常直觉中 “概率就是长期频率” 的想法提供了严格的数学基础。它是概率论中几种更一般形式的大数法则的一个特例。

5. 弱大数法则的证明

　　 设 $X_1, X_2, \ldots$ 是一个无限的独立同分布（i.i.d.）随机变量序列，其期望值有限，即 $$ E(X_1) = E(X_2) = \cdots = \mu < \infty,~ $$ 我们关注样本均值的收敛性： $$ \overline{X}_n = \frac{1}{n}(X_1 + \cdots + X_n).~ $$ 弱大数法则陈述如下： $$ \overline{X}_n \overset{P}{\longrightarrow} \mu \quad \text{当 } n \to \infty.~ $$ 也就是说，样本均值在概率意义下收敛于期望值 $\mu$。

使用切比雪夫不等式证明（假设方差有限

　　 此证明基于以下假设：每个随机变量 $X_i$ 都具有有限方差：$\operatorname{Var}(X_i) = \sigma^2 \quad \text{（对所有 } i \text{成立）}$ 由于这些随机变量是独立的，因此它们之间不相关。于是我们有： $$ \operatorname{Var}(\overline{X}_n) = \operatorname{Var}\left(\frac{1}{n}(X_1 + \cdots + X_n)\right) = \frac{1}{n^2} \operatorname{Var}(X_1 + \cdots + X_n) = \frac{n\sigma^2}{n^2} = \frac{\sigma^2}{n}~ $$ 整个序列的公共期望值为 $\mu$，也是样本均值的期望值： $$ E(\overline{X}_n) = \mu~ $$ 在 $\overline{X}_n$ 上应用切比雪夫不等式得到： $$ \operatorname{P}(|\overline{X}_n - \mu| \geq \varepsilon) \leq \frac{\sigma^2}{n\varepsilon^2}~ $$ 由此可以得到： $$ \operatorname{P}(|\overline{X}_n - \mu| < \varepsilon) = 1 - \operatorname{P}(|\overline{X}_n - \mu| \geq \varepsilon) \geq 1 - \frac{\sigma^2}{n\varepsilon^2}~ $$ 随着 $n \to \infty$，上式趋近于 1。根据概率收敛的定义，我们由此得出： $$ \overline{X}_n \overset{P}{\longrightarrow} \mu \quad \text{当 } n \to \infty~ $$

使用特征函数收敛性进行的证明

　　 根据复函数的泰勒定理，任意具有有限均值 $\mu$ 的随机变量 $X$ 的特征函数可以写为： $$ \varphi_X(t) = 1 + it\mu + o(t), \quad t \to 0~ $$ 由于所有的 $X_1, X_2, \ldots$ 都是独立同分布的，它们具有相同的特征函数，记作 $\varphi_X$。 特征函数的一些基本性质如下： $$ \varphi_{\frac{1}{n}X}(t) = \varphi_X\left(\frac{t}{n}\right),\quad \text{以及（若 } X, Y \text{ 独立）} \quad \varphi_{X+Y}(t) = \varphi_X(t)\varphi_Y(t)~ $$ 这些性质可以用来计算样本均值 $\overline{X}_n$ 的特征函数： $$ \varphi_{\overline{X}_n}(t) = \left[\varphi_X\left(\frac{t}{n}\right)\right]^n = \left[1 + i\mu \frac{t}{n} + o\left(\frac{t}{n}\right)\right]^n \longrightarrow e^{it\mu} \quad \text{当 } n \to \infty ~ $$ 极限 $e^{it\mu}$ 是常随机变量 $\mu$ 的特征函数，因此根据 Lévy 连续性定理，样本均值 $\overline{X}_n$ 在分布意义上收敛于 $\mu$： $$ \overline{X}_n \xrightarrow{\mathcal{D}} \mu \quad \text{当 } n \to \infty~ $$ 由于 $\mu$ 是常数，因此收敛于常数的分布收敛与概率收敛是等价的（见随机变量收敛的类型）。因此，我们得出： $$ \overline{X}_n \xrightarrow{P} \mu \quad \text{当 } n \to \infty~ $$ 这就证明了：只要特征函数在原点处的导数存在，样本均值就以概率意义收敛于该导数所对应的期望值 $\mu$。

6. 强大数法则的证明

　　 我们将在以下假设下给出一个相对简单的强大数法则证明：$X_i$ 是独立同分布（i.i.d.）的；$\mathbb{E}[X_i] =: \mu < \infty$；$\operatorname{Var}(X_i) = \sigma^2 < \infty$；$\mathbb{E}[X_i^4] =: \tau < \infty$。

　　 我们首先说明：不失一般性地可以假设 $\mu = 0$，这是通过 “中心化” 操作实现的（即用 $X_i - \mu$ 代替 $X_i$）。在这种情况下，强大数法则的陈述为： $$ \Pr\left(\lim_{n \to \infty} \overline{X}_n = 0\right) = 1,~ $$ 或者写作： $$ \Pr\left(\omega : \lim_{n \to \infty} \frac{S_n(\omega)}{n} = 0\right) = 1,~ $$ 其中 $S_n = \sum_{i=1}^n X_i$。

　　 这等价于要证明： $$ \Pr\left(\omega : \lim_{n \to \infty} \frac{S_n(\omega)}{n} \neq 0\right) = 0.~ $$ 注意： $$ \lim_{n \to \infty} \frac{S_n(\omega)}{n} \neq 0 \iff \exists\, \epsilon > 0, \left|\frac{S_n(\omega)}{n}\right| \geq \epsilon \text{ infinitely often},~ $$ 因此，要证明强大数法则，我们只需证明对于每个 $\epsilon > 0$ 都有： $$ \Pr\left(\omega : |S_n(\omega)| \geq n\epsilon \text{ infinitely often}\right) = 0.~ $$ 定义事件：$A_n := \{\omega : |S_n| \geq n\epsilon\}$ 如果我们能证明级数： $$ \sum_{n=1}^{\infty} \Pr(A_n) < \infty,~ $$ 那么根据 Borel-Cantelli 引理，我们就能得出所需的结论。接下来我们估算 $\Pr(A_n)$。为此，考虑四阶矩： $$ \mathbb{E}[S_n^4] = \mathbb{E}\left[\left(\sum_{i=1}^n X_i\right)^4\right] = \mathbb{E}\left[\sum_{1 \leq i, j, k, l \leq n} X_i X_j X_k X_l\right].~ $$ 我们首先断言，所有形如 $X_i^3 X_j, \quad X_i^2 X_j X_k, \quad X_i X_j X_k X_l$ 且所有下标互不相同的项，其期望值都为零。这是因为 $\mathbb{E}[X_i^3 X_j] = \mathbb{E}[X_i^3] \cdot \mathbb{E}[X_j]$ 依据独立性成立，而由于 $\mathbb{E}[X_j] = 0$，所以结果为零。其他类似项的推理相同。因此，在和式中唯一可能具有非零期望的项是 $\mathbb{E}[X_i^4] \quad \text{和} \quad \mathbb{E}[X_i^2 X_j^2]$。由于各 $X_i$ 独立同分布，这些项都相等，并且 $\mathbb{E}[X_i^2 X_j^2] = \left( \mathbb{E}[X_i^2] \right)^2$。

　　 在总和中，具有 $\mathbb{E}[X_i^4]$ 形式的项共有 $n$ 个，具有 $\left( \mathbb{E}[X_i^2] \right)^2$ 形式的项共有 $3n(n - 1)$ 个，因此： $$ \mathbb{E}[S_n^4] = n \tau + 3n(n - 1) \sigma^4.~ $$ 注意，右侧是关于 $n$ 的一个二次多项式，因此存在常数 $C > 0$，使得当 $n$ 足够大时，有：$\mathbb{E}[S_n^4] \leq C n^2$ 根据 Markov 不等式： $$ \Pr(|S_n| \geq n \epsilon) \leq \frac{1}{(n \epsilon)^4} \mathbb{E}[S_n^4] \leq \frac{C}{\epsilon^4 n^2}~ $$ 当 $n$ 足够大时成立。于是这个概率构成的级数是可求和的。

　　 由于上述结论对任意 $\epsilon > 0$ 都成立，我们就得出了强大数法则的证明。 这个证明还可以在不假设有限二阶或四阶矩的条件下进一步加强。例如，它也可以扩展到研究没有任何有限矩的分布的部分和情形。这类证明使用更复杂的技巧来验证相同的 Borel-Cantelli 判定句，这是 Kolmogorov 提出的策略，其思想是在概念上将极限带入概率符号内部。

7. 结果推论

　　 大数法则不仅可以通过一组样本值来估计未知分布的期望，还可以估计概率分布的任何特征。[1]利用 Borel 大数法则，可以很容易地获得概率质量函数（PMF）。对于目标概率质量函数中的每一个事件，我们可以用该事件发生的频率来逼近其概率。重复次数越多，逼近效果就越好。对于连续情形：令 $C = (a - h, a + h]$ 其中 $h > 0$ 很小。那么当样本数 $n$ 足够大时，有： $$ \frac{N_n(C)}{n} \approx p = P(X \in C) = \int_{a-h}^{a+h} f(x)\,dx \approx 2h f(a)~ $$ 使用这种方法，我们可以用间隔为 $2h$ 的网格覆盖整个 $x$ 轴，并得到一个条形图，这种图就被称为直方图。

8. 应用

　　 大数法则的一个重要应用是蒙特卡洛方法[3]，这是一种利用随机抽样来近似数值结果的重要逼近方法。用它来计算函数 $f(x)$ 在区间 $[a, b]$ 上的积分的算法如下：\(^\text{[3]}\)

  1. 模拟均匀随机变量 $X_1, X_2, \ldots, X_n$：这可以通过软件实现，或使用提供独立同分布（i.i.d.）的 $[0, 1]$ 区间随机变量 $U_1, U_2, \ldots, U_n$ 的随机数表。然后令 $X_i = a + (b - a) U_i,\quad i = 1, 2, \ldots, n.$ 这样，$X_1, X_2, \ldots, X_n$ 就是定义在 $[a, b]$ 上的独立同分布均匀随机变量。
  2. 计算函数值：对这些样本点分别计算 $f(X_1), f(X_2), \ldots, f(X_n)$。
  3. 取平均值并乘以区间长度：$(b - a) \cdot \frac{f(X_1) + f(X_2) + \cdots + f(X_n)}{n}$ 根据**强大数法则**，该平均值几乎必然收敛于 $$ (b - a) \cdot \mathbb{E}[f(X_1)] = (b - a) \cdot \int_a^b f(x) \cdot \frac{1}{b - a} \, dx = \int_a^b f(x)\,dx.~ $$ 因此，这种方法可以用来近似积分的真实值。

　　 我们可以计算函数 $f(x) = \cos^2(x)\sqrt{x^3 + 1}$ 在区间 $[-1, 2]$ 上的积分。使用传统方法求这个积分非常困难，因此可以使用蒙特卡洛方法来处理。[3] 根据上述算法，我们得到：

　　 当 $n = 25$ 时， $$ \int_{-1}^{2} f(x)\,dx = 0.905~ $$ 当 $n = 250$ 时， $$ \int_{-1}^{2} f(x)\,dx = 1.028~ $$ 我们可以观察到，随着样本数量 $n$ 的增加，数值解也在逐步接近实际值。实际积分结果为： $$ \int_{-1}^{2} f(x)\,dx = 1.000194~ $$ 使用大数法则（LLN）时，积分的近似值更接近真实值，因此结果更准确。[3]另一个例子是对函数 $f(x) = \frac{e^x - 1}{e - 1}$ 在区间 $[0, 1]$ 上进行积分。[34] 通过使用蒙特卡洛方法和大数法则，可以看到，随着样本数量的增加，数值结果不断接近 0.4180233。[34]

9. 参见

10. 注释

  1. Dekking, Michel（2005 年）。《现代概率与统计导论》。Springer，第 181–190 页。ISBN 9781852338961。
  2. Yao, Kai；Gao, Jinwu（2016 年）。“不确定随机变量的大数法则”。发表于 *IEEE Transactions on Fuzzy Systems*，第 24 卷第 3 期，第 615–621 页。doi:10.1109/TFUZZ.2015.2466080。ISSN 1063-6706。S2CID 2238905。
  3. Sedor, Kelly。“大数法则及其应用”。
  4. Kroese, Dirk P.; Brereton, Tim; Taimre, Thomas; Botev, Zdravko I.（2014 年）。《为何蒙特卡洛方法在当今如此重要》。发表于 *Wiley Interdisciplinary Reviews: Computational Statistics*，第 6 卷第 6 期，第 386–392 页。doi:10.1002/wics.1314。hdl:1959.4/unsworks_43203。S2CID 18521840。
  5. Dekking, Michel, 编（2005 年）。《现代概率与统计导论：理解为何以及如何》。Springer 统计学教材。伦敦 [海德堡]：Springer，第 187 页。ISBN 978-1-85233-896-1。
  6. Dekking, Michel（2005 年）。同上，第 92 页。
  7. Dekking, Michel（2005 年）。同上，第 63 页。
  8. Pitman, E. J. G.; Williams, E. J.（1967 年）。《柯西变量的柯西分布函数》。发表于 *The Annals of Mathematical Statistics*，第 38 卷第 3 期，第 916–918 页。doi:10.1214/aoms/1177698885。ISSN 0003-4851。JSTOR 2239008。
  9. Mlodinow, L.（2008 年）。《醉汉的漫步》。纽约：Random House，第 50 页。
  10. Bernoulli, Jakob（1713 年）。《第 4 章》。概率的艺术：前述理论在政治、伦理及经济领域的应用（*Ars Conjectandi: Usum & Applicationem Praecedentis Doctrinae in Civilibus, Moralibus & Oeconomicis*，拉丁文）。由 Oscar Sheynin 翻译。
  11. Poisson 首次命名 “大数法则”：Poisson, S. D.（1837 年）。刑事和民事审判中的概率，附带概率计算的一般规则。法国巴黎：Bachelier，第 7 页。他试图在第 139–143 页和第 277 页以后对该法则进行两部分证明。
  12. Hacking, Ian（1983 年）。《19 世纪决定论概念的裂痕》。发表于 Journal of the History of Ideas，第 44 卷第 3 期，第 455–475 页。doi:10.2307/2709176。JSTOR 2709176。
  13. Tchebichef, P.（1846 年）。《概率理论一则一般命题的初等证明》。发表于 Journal für die reine und angewandte Mathematik（法文），1846 年第 33 期，第 259–267 页。doi:10.1515/crll.1846.33.259。S2CID 120850863。
  14. Seneta 2013。
  15. Yuri Prohorov。“大数法则”。发表于 数学百科全书，EMS Press。
  16. Bhattacharya, Rabi；Lin, Lizhen；Patrangenaru, Victor（2016 年）。《数理统计与大样本理论课程》。Springer 统计教材系列。纽约州纽约市：Springer New York。doi:10.1007/978-1-4939-4032-5。ISBN 978-1-4939-4030-1。
  17. “强大数法则——有什么新内容？”。Terrytao.wordpress.com。2008 年 6 月 19 日发布，2012 年 6 月 9 日访问。
  18. Etemadi, N. Z.（1981 年）。“强大数法则的一个初等证明”。发表于 Wahrscheinlichkeitstheorie Verw Gebiete，第 55 卷第 1 期，第 119–122 页。doi:10.1007/BF01013465。S2CID 122166046。
  19. Kingman, J. F. C.（1978 年 4 月）。“交换性的应用”。发表于 *The Annals of Probability*，第 6 卷第 2 期。doi:10.1214/aop/1176995566。ISSN 0091-1798。
  20. Loève（1977 年），第 1.4 章，第 14 页。
  21. Loève（1977 年），第 17.3 章，第 251 页。
  22. Yuri Prokhorov。“强大数法则”。发表于 数学百科全书。
  23. “什么是大数法则？（定义）| Built In”。builtin.com，2023 年 10 月 20 日访问。
  24. Ross（2009 年）。
  25. Lehmann, Erich L.;Romano, Joseph P.（2006 年 3 月 30 日）。*Weak law converges to constant*。Springer。ISBN 9780387276052。
  26. Dguvl Hun Hong；Sung Ho Lee（1998 年）。“关于交换随机变量的弱大数法则的一则注记”（PDF）。发表于 韩国数学会通讯，第 13 卷第 2 期，第 385–391 页。PDF 原文于 2016 年 7 月 1 日存档，2014 年 6 月 28 日访问。
  27. Mukherjee, Sayan。“大数法则”（PDF）。PDF 原文于 2013 年 3 月 9 日存档，2014 年 6 月 28 日访问。
  28. Geyer, Charles J.。“大数法则”（PDF）。
  29. Newey 与 McFadden（1994 年），引理 2.4。
  30. Jennrich, Robert I.（1969 年）。“非线性最小二乘估计量的渐近性质”。发表于 数学统计年刊，第 40 卷第 2 期，第 633–643 页。doi:10.1214/aoms/1177697731。
  31. Wen, Liu（1991 年）。“证明 Borel 强大数法则的一种解析方法”。发表于 美国数学月刊，第 98 卷第 2 期，第 146–148 页。doi:10.2307/2323947。JSTOR 2323947。
  32. 另一个证明来自 Etemadi, Nasrollah（1981 年）。“强大数法则的一个初等证明”。发表于 Zeitschrift für Wahrscheinlichkeitstheorie und verwandte Gebiete，第 55 卷。Springer，第 119–122 页。doi:10.1007/BF01013465。S2CID 122166046。
  33. 若不假设有限四阶矩的证明，参见 Billingsley, Patrick（1979 年）所著 Probability and Measure 第 22 节。
  34. Reiter, Detlev（2008 年），收录于 Fehske, H.; Schneider, R.; Weiße, A.（主编），“蒙特卡洛方法导论”，《多粒子计算物理学教程》，Lecture Notes in Physics，第 739 卷，柏林、海德堡：Springer Berlin Heidelberg，第 63–78 页，doi:10.1007/978-3-540-74686-7_3，ISBN 978-3-540-74685-0，2023 年 12 月 8 日访问。

11. 参考文献

12. 外部链接

                     

© 保留一切权利