苏州大学 2005 年硕士考试试题

                     

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

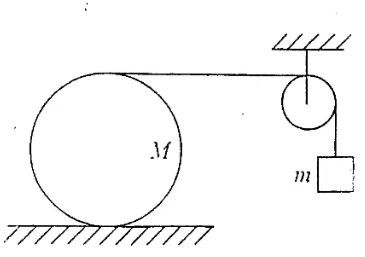
  1. 质量为 $M$，半径为 $r$ 的均匀圆柱体放在粗糙的水平面上，柱的外围绕有轻绳，绳子绕过一个很轻的滑轮，并悬挂一质量为 $m $ 的物体。设圆柱只滚不滑，并且圆柱体与滑轮间的绳子是水平的，求圆柱体质心加速度 $ a_1$、物体的加速度 $ a_2$、及绳中张力 T。
    图
    图 1
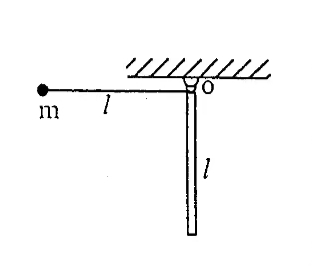
  2. 如图所示，长为 $l$ 的质细杆，一端悬于 O 点,自由下垂。在 O 点同时悬一单摆，摆长也是 $l$，摆的质量为 $m$，单摆从水平位置由静止开始自由下摆，与自由下垂的细杆作完全弹性碰撞,碰撞后单摆恰好静止。求:
    (1)细棒的质量 $M;$
    (2)细棒摆动的最大角度 $\theta$。
    图
    图 2
  3. 一弹簧振子作简偕振动，振幅 $A=0.20m$，如果弹簧的劲度系数 $k=2.0N/m$ 所系物体的质量 $m=0.50kg$，试求:
    (1)当动能和势能相等时，物体的位移是多少?
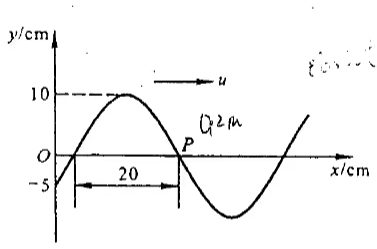
    (2)设 $t=0$ 时，物体在正最大位移处，达到动能和势能相等处所需的时间是多少(在一个周期内)?
  4. 已知一沿 $x$ 轴正方向传播的平面余弦波在 $t=\frac{1}{3}$ 秒时的波形如图所示，且周期 $T=2S$。求
    (1)写出 O 点和 P 点的振动表达式。
    (2)写出该波的波动表达式。
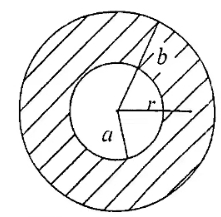
    (3)求 P 点离 Os 点的距离。
    图
    图 3
  5. 图中球形区域 $a< r< b$，设其体密度为 $\rho=A/r$，在封闭空腔的中心($r=0$)有一个电量为 Q 的点电荷。证明:当 A$=Q/2\pi a^2$ 时，球形区域($a< r< b$)中的电场具有恒定值。
    图
    图 4
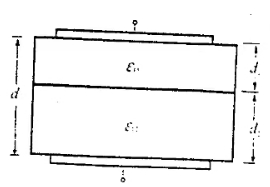
  6. 一平行板电容器有两层介质，$\varepsilon_{r_1}=4,\varepsilon_{r_2}=2$,厚度为 $ d_1=2.0mm$，$d_2=3.0mm$，极板面积 $S=40cm^2$，两极板电压为 $200V$。计算:
    (1)每层介质中的电场能量密度;
    (2)每层介质中的总能量;
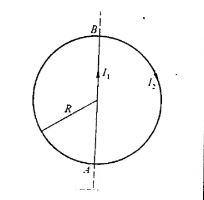
    (3)用公式 $\frac{1}{2}qU$ 计算电容器的总能量。
    图
    图 5
  7. 半径为 $R$ 的平面圆形线圈中载有电流 $I_2$，另一无限长直线 $AB $ 中载有电流 $I_1$，设 $AB$ 通过圆心,并和圆形线圈在同一平面内(如图)，求圆形线圈所受的磁力。
    图
    图 6
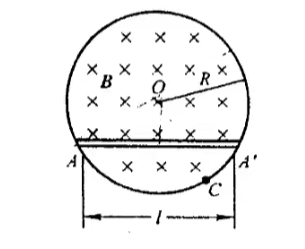
  8. 在半径为 $R$ 的圆柱形体积内充满磁感应强度为 $B$ 的均匀磁场，有一长为 $l$ 的金属棒放在磁场中，如图所示。设 $dB/dt $ 为已知，求棒两端的电势差。
    图
    图 7
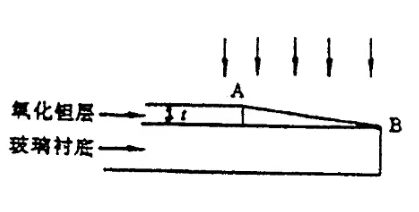
  9. 如图所示，沉积在玻璃衬底上的氧化钽层从 $A$ 到 $B$ 的厚度递减到零，从而形成一尖劈，为测定氧化钽薄层的厚度 $t$，用波长为 $632.8nm$ 的 He-Ne 激光垂直照射到薄层上,观察到楔形部分共出现 11 条暗纹，且 $A$ 处恰好为一暗纹位置，已知氧化胆的折射率 $n_1$=2.21，玻璃折射率 $n_2$=1.5，求氧化胆薄层的厚度 $t$。
    图
    图 8
  10. 含有二种波长 $\lambda_1$、$\lambda_2$ 的光垂直入射在每毫米有 300 条缝的衍射光栅上，已知 $\lambda_1$ 为红光，$\lambda_2$ 为紫光，在 24°角处二种波长光的谱线重合。求:
    (1)紫光的波长 $\lambda_2$。
    (2)屏幕上可能单独呈现紫光的各级谱线的级次(只需写出正级次)
  11. 老鹰眼睛的瞳孔直径不大于 $ 8mm$，可见光波长 $400~700nm$，计算说明飞翔于 1000 米高空的鹰是否能看清地面上身长为 $5cm$ 的小鼠。
  12. 偏振光干涉实验装置中，两偏振片透光轴之间的夹角为 60°，方解石波片的光轴放在两偏振片透光轴夹角的角平分线位置，如果入射单色自然光强为 $I_0$，求:
    (1)从方解石波片出射的 o 光利 e 光的振幅和光强;
    (2)从第二块偏振片出射的。光和 e 光的振幅和光强。

                     

© 小时科技 保留一切权利