四川大学 2013 年硕士物理考试试题(933)
贡献者: 待更新
声明:“该内容来源于网络公开资料,不保证真实性,如有侵权请联系管理员”
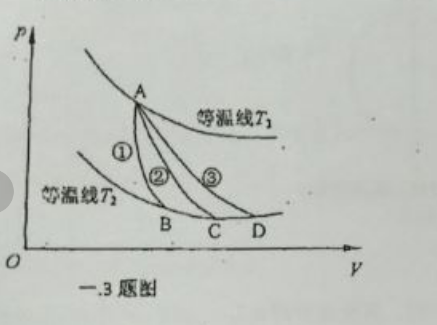
1.(本题 8 分)
如一,3 题图所示,一理想气体分别经①、②、③过程出 $A$ 状态到达 $B,C,D$ 状态,其中②)是绝热过程。试分析这三个过程中哪些是吸热过程,哪些是放热过程。
2.(本题 6 分)
有直径为 $16cm$ 及 $10cm$ 的非常薄的两个铜制球壳,同心放置时,内球的电势为 $2700V$,外球带有电荷量为 $8.0\times10^{-9}C$。现把内球和外球接触,两球的电势各变化多少 $(\varepsilon_0=8.85\times10^{-12} C^2/(N\cdot m^2))$
3.(本题 6 分)
所示的三个闭合回路 1、2、3,分别写出磁感应强度 $B$ 沿它们的环流值。设 $I_1=I_2=I$。并讨论:
- 在每个闭合回路上各点的 $B$ 值是否相等?
- 在回路 3 上各点的 $B$ 是否均等于零?
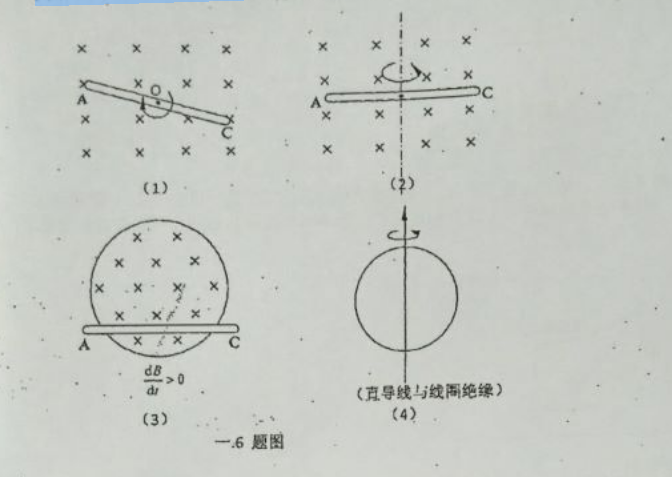
4.(本题 8 分)
判断下列各一.6 题图中的导线段 AC.或者导线框内的感应电动势的方向。
5.(本题 6 分)
钠黄光中包含着两条相近的谱线,其波长分别为 $\lambda_1=589.0nm$ 和 $\lambda_2=589.6nm$。用钠黄光照射迈克耳孙干涉仪,当干涉仪的可动反射镜连续地移动时,视场中的干涉条纹将周期性地由清晰逐渐变模糊,再逐渐变清晰,再变模糊,….求视场中的干涉条纹某一次由最清晰变为最模糊的过程中可动反射镜移动的距离 $d$.
6.(本题 6 分)
一台望远镜物镜的直径为 $3.5m$,对子平均波长入 $\lambda=550nm$ 的可见光,其最小分辨角为多少?其正常放大率为多少?(人眼的分辨极限角 $\theta=1'-2.9\times10^{-4}rad$)
7.(本题 6 分)
对于自然光,圆偏振光,线偏振光,你如何通过实验做出判别?
1. 计算题(共 90 分)。
1、(本题 10 分)
一体积为 $10\times10\times3m^3$ 的密封房间,室温为 27℃,已知空气的密度。$\rho=1.29kg/m$ 摩尔质量 $29x10^{-3}kg/mol$,且空气分子可认为是刚性双原子分子。$(R=8.31J/(mol\cdot K))$。 求
- 室内空气分子热运动的平均平动动能的总和是多少?
- 如果气体的温度升高 $1.0K$,而体积不变,则气体的内能变化多少?
- 气体分子的方均根速率增加多少?
2、(本题 12 分)
$3mol$ 氧气在压强为 2 个标准大气压时的体积为 $40L$,先将它绝热压缩到体积的一半,再令它等温膨胀回原来的体积。求在这一过程中氧气吸收的热量、对外做的功以及内能的变化。
3、(本题 8 分)
一定量的理想气体经历如二 3 题图所示的循环过程,$A\to B$ 和 $C\to D$ 是等压过程,$B\to C$ 和 $D\to A$ 是绝热过程。已知:7=300K,7=400K,试求:此环的效率。
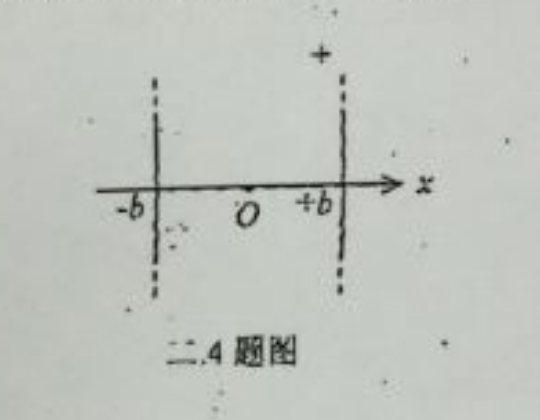
4、(本题 10 分)
电荷面密度分别为 $+\sigma$ 和 $-\sigma$ 的两块无限大均匀带电平行平面,分别与 x 轴垂直相交于 $x_1 = b, x_2 = -b$ 两点,如图 2.4 图所示。设坐标原点 $O$ 处电势为零,试求空间的电势分布表示式并画出其曲线。
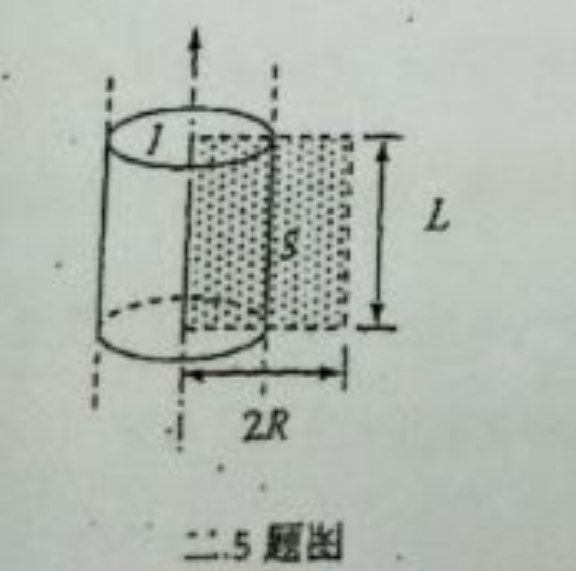
5、(12 分)
一无限长圆柱形铜导体(磁导率 $\mu_0$),半径为 $R$,通有均匀分布的电流 $I$。今取一矩形平面 $S$(长为 $L$,宽为 $2R$),位置如二 5 题图中阴影部分所示,求通过该矩形平面的磁量。
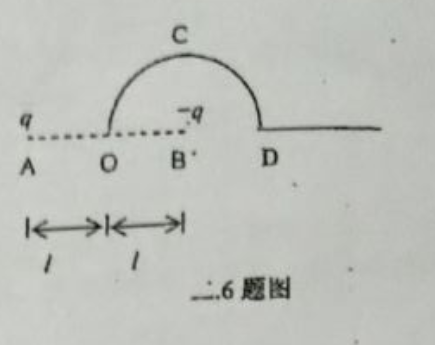
6、(8 分)
如题 6 图所示,$A,O,B,D$ 在一直线上,间距如图所示。$ OCD $ 是半径为 $l$ 的半圆。
$A$ 点和 $B$ 点分别有电荷量为 $+q$ 和 $-q$ 的电荷,试求:
- 把单位正电荷从 $O$ 点沿半圆弧 $ OCD $ 移动到 $D$ 点,电场力做的功。
- 把单位负电荷从 $D$ 点沿 $AD$ 的延长线移动到无穷远处,电场力做的功。
7、(本题 10 分)
在某个单缝衍射实验中,光源发出的光合有两种波长 $\lambda_1$ 和 $\lambda_2$,并垂直入射于单趟上。假如 $\lambda_1$ 的第一级衍射极小与 $\lambda_2$ 的第二银衍射极小相重合,试问家 .6 题图
- 这两种波长之间有何关系?
- 在这两种波长的光所形成的衍射图样中,是否还有其它极小相重合?
8、(本题 12 分)
用一石英薄片来产生一束椭圆骗振光,要使椭圆的长轴或短轴在光轴方向,长短轴之比为 2:1,且是左旋的。问石英片应为多厚?如何放置?$(\lambda=589.3nm,n_0=1.544298,n_e=1.5533)$
9.(本题 8 分)
一东直径为 $2mm$ 的氮氖微光($\lambda=632.8nm$)自地面射向月球。已知月球离地面的距高为 $3.76\times10^5km$,问在月球上得到的光斑有多大(不计大气的影响)?若把这样的激光東经扩東器扩大到直径为 $2m$ 和 $5m$ 后再发射,月球上的光斑各有多大?