球极平面投影

贡献者：待更新

　　（本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

图 1：从圆球面北极点向球面底部平面投影的三维示意图

　　在几何中，球极平面投影是一种将圆球面投影到平面上的特殊映射(函数)。该映射的定义域为除投影点外的整个球面。在定义域内，该映射具有光滑性、双射性和共形性。共形性意味着其为保持曲线相交角度不变的映射。但是，该映射既不保距离也不保面积：也就是说，其既不能维持映射后图形的距离不变，也不能维持映射后图形的面积不变。

　　直观地说，球极平面投影是一种用平面来描绘球面的方法，但该方法在图案品质方面，也包含一些不可避免的妥协。因为球面和平面出现于数学及其应用的诸多领域，所以球极平面投影也同样很常见。在各个领域，例如复分析、制图学、地质学、摄影等，球极平面投影都有广泛的应用。在实践中，球极平面投影通常是通过计算机或手工在一种称为立体球面投影网的特殊的方格纸上绘制完成，该立体球面投影网简称立体网，或乌尔夫网。

1. 历史

图 2：鲁本斯(Rubens)为弗朗索瓦·达吉隆(François d'Aguilon)的著作《光学六册：适用于哲学家和数学家》所作的插图。该图展现了一般透视投影的原理，球极平面投影是其中一种特殊情况。

　　球极平面投影为希帕克斯(Hipparchus)、托勒密(Ptolemy)，甚至可能更早期的古埃及人所知。其最初被称为 “平面天体投影”。[1] 托勒密的著作《平球论》（Planisphaerium）是现存最古老的描述球极平面投影的文献，其最重要的用途之一就是描绘天体图。[1] “平面天体投影” 这个术语仍然用于指代这样的图表。

　　在 16 世纪和 17 世纪，球极平面投影的赤道面通常被用于东半球和西半球地图上。通常认为，1507 年瓜尔特里厄斯·路德(Gualterius Lud)绘制的地图[2] 使用的就是球极平面投影，包括后来的让·罗兹(Jean Roze)(1542 年)、鲁莫尔德·墨卡托(Rumold Mercator)(1595 年)，以及其他许多人绘制的地图。[3] 而在星图上，这个赤道面也已经被像托勒密这样的古代天文学家利用了。[4]

　　弗朗索瓦·德阿吉隆(François d'Aguilon)在他 1613 年的著作《光学六册：适用于哲学家和数学家》（Opticorum libri sex philosophis juxta ac mathematicis utiles）中给球极平面投影取了现在的名字。[5]

　　 1695 年，在兴趣的驱使下，埃德蒙多·哈雷(Edmond Halley)发表了第一篇关于星图共形性的数学证明。[6] 在证明中，他使用了由他的朋友艾萨克·牛顿(Isaac Newton)在当时刚刚建立起来的微积分工具。

2. 定义

2.1 第一类计算公式

图 3：单位球面上从北极点向 z = 0 平面的球极平面投影的截面示意图

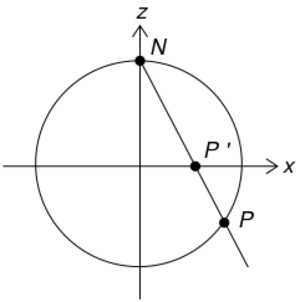
　　三维空间 $\mathbb{R}^3$ 中的单位球面是一组点 $(x, y, z)$ 的集合，且满足 $x^2 + y^2 + z^2 = 1$。如果令点 $N = (0, 0, 1)$ 为该球面上的 “北极点”，令球面的其余部分为 $M$，则 $z = 0$ 平面穿过该球面所包裹的球体的中心，“赤道” 就是球面与 $z = 0$ 平面的交线。

　　对于 $M$ 上的任意一点 $P$，有且仅有一条直线穿过 $N$ 和 $P$ 点，且这条线与 $z = 0$ 平面相交于 $P'$ 点。定义 $P$ 点在 $z = 0$ 平面上的球极平面投影为 $P'$ 点。

　　在笛卡尔坐标系中，球面上的坐标 $(x, y, z)$ 与对应的平面上的坐标 $(X, Y)$ 满足以下投影及其逆投影关系式： $$(X, Y) = \left( \frac{x}{1 - z}, \frac{y}{1 - z} \right),~$$ $$(x, y, z) = \left( \frac{2X}{1 + X^2 + Y^2}, \frac{2Y}{1 + X^2 + Y^2}, \frac{-1 + X^2 + Y^2}{1 + X^2 + Y^2} \right).~$$ 在球面坐标系中，球面上的坐标 $(\varphi, \theta)$（用 $\varphi$ 表示天顶角，$0 \leq \varphi \leq \pi$；用 $\theta$ 表示方位角，$0 \leq \theta \leq 2\pi$）与对应的平面上的极坐标 $(R, \Theta)$ 满足以下投影及其逆投影关系式： $$(R, \Theta) = \left( \frac{\sin \varphi}{1 - \cos \varphi}, \theta \right) = \left( \cot \frac{\varphi}{2}, \theta \right),~$$ $$(\varphi, \theta) = \left( 2 \arctan \frac{1}{R}, \Theta \right).~$$ 这里，定义当 $R = 0$ 时 $\varphi = \pi$。此外，可以用与上述公式等价的方式将这些公式改写为多种不同的形式。在圆柱坐标中，球面上的坐标 $(r, \theta, z)$ 与对应的平面上的极坐标 $(R, \Theta)$ 满足以下投影及其逆投影关系式： $$(R, \Theta) = \left( \frac{r}{1 - z}, \theta \right),~$$ $$(r, \theta, z) = \left( \frac{2R}{1 + R^2}, \Theta, \frac{R^2 - 1}{R^2 + 1} \right).~$$

2.2 其他约定形式

图 4：单位球面上从北极点向 z = −1 平面的球极平面投影的截面示意图

　　一些作者[7] 将球极平面投影定义为从单位球面上的北极点 (0, 0, 1) 向 z = −1 平面的投影，该平面与单位球面的南极点(0, 0, −1) 相切。这种极点切面所得到的 $X$ 和 $Y$ 的坐标值恰好是上一节描述的赤道平面投影坐标值的两倍。例如，该投影将赤道映射为以原点为中心，半径为 2 的圆。可以看出，赤道平面投影在赤道上不会产生无穷小的面积变形，而极点切面投影在南极不会产生无穷小的面积变形。

　　还有其他一些作者[8] 使用半径为 12 的球面和 z = − 12 平面来定义球极平面投影。在这种情况下，计算公式为： $$(x, y, z) \rightarrow (\xi, \eta) = \left( \frac{x}{\frac{1}{2} - z}, \frac{y}{\frac{1}{2} - z} \right),~$$ $$(\xi, \eta) \rightarrow (x, y, z) = \left( \frac{\xi}{1 + \xi^2 + \eta^2}, \frac{\eta}{1 + \xi^2 + \eta^2}, \frac{-1 + \xi^2 + \eta^2}{2 + 2\xi^2 + 2\eta^2} \right).~$$

图 5：从球面上一点 Q 向平面 E 的球极平面投影的截面示意图

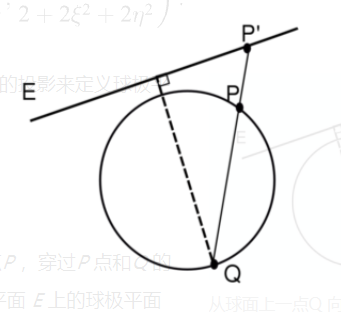
　　一般来说，可以用从球面上的任意一点 $Q$ 向任意平面 $E$ 的投影来定义球极平面投影，只需要满足：

平面 $E$ 垂直于穿过 $Q$ 点的直径；
平面 $E$ 中不包含 $Q$ 点。

　　那么在这种情况下，对于球面上除 $Q$ 点以外的任意一点 $P$，穿过 $P$ 点和 $Q$ 的直线将与平面 $E$ 相交于 P′点，而 P′点就定义为 $P$ 点在平面 $E$ 上的球极平面投影。[9]

2.3 一般化

　　更一般地，球极平面投影可以应用于 $(n + 1)$ 维欧几里得空间 $E^{n+1}$ 中的 $n$ 维球体 $S^n$ 上。假设 $Q$ 是 $n$ 维球体 $S^n$ 上的一点，且 $E$ 为 $E^{n+1}$ 空间中的一个超平面，那么球面上一点 $P \in S^n - \{Q\}$ 的球极平面投影 $P'$ 就是直线 $QP$ 与超平面 $E$ 的交点。如果从点 $Q = (1, 0, 0, \ldots, 0)$ 进行投影，那么在笛卡尔坐标系中，球面上点的坐标 $(x_i; i = 0, 1, 2, \ldots, n)$ 与对应的平面上的点的坐标 $(X_i; i = 1, 2, \ldots, n)$ 之间的投影关系由下式给出： $$X_i = \frac{x_i}{1 - x_0} \quad (i = 1, 2, \ldots, n)~$$ 如果定义： $$S^2 = \sum_{j=1}^n x_j^2~$$ 则逆投影关系可由下式给出： $$x_0 = \frac{S^2 - 1}{S^2 + 1}; \quad x_i = \frac{2X_i}{S^2 + 1} \quad (i = 1, 2, \ldots, n)~$$ 更一般地，假设 $S$ 是射影空间 $P^{n+1}$ 中的一个（非奇异）二次超曲面。换句话说，$S$ 是非奇异二次型 $f(x_0, \ldots, x_{n+1})$ 在齐次坐标 $x_i$ 中的零轨迹。固定 $S$ 上的任何一点 $Q$ 以及 $P^{n+1}$ 中一个不包含 $Q$ 点的超平面 $E$。那么 $S - \{Q\}$ 上任意一点 $P$ 的球极平面投影就是 $QP$ 与 $E$ 的唯一交点。和前面一样，球极平面投影在 “小” 集合之外是共形且可逆的。球极平面投影将二次超曲面表示为有理超曲面。这种结构在代数几何和共形几何中发挥了重要作用。

图 6：立体投影和一些方位投影的比较，以相同比例的 90° N 为中心，按地球半径投影高度排序。(click for detail)

3. 性质

　　前面部分定义的第一个球极平面投影方法是将单位球面的 “南极点”(0, 0, −1)映射到平面上的(0, 0)点，将赤道映射到平面上单位圆，南半球面映射到单位圆内区域，北半球面映射到单位圆外区域。

　　该投影方法在投影点 $N = (0, 0, 1)$ 处无定义。该点的小邻域被映射到远离(0, 0)点的平面子集内。$P$ 点离(0, 0, 1)点越近，其在平面上的投影点就离(0, 0)点越远。由于这个原因，通常会把(0, 0, 1)点映射到平面上的 “无穷远” 处，通过添加无穷远点实现完整的球面到平面的映射。这个概念在射影几何和复分析中很有用。仅在拓扑层面上，它说明了球面如何与平面的单点紧化同胚。

　　笛卡尔坐标中，对于球面上一个点 $P(x, y, z)$ 与对应的平面上的点 P′(X, Y)，要么两者都是有理点，要么都不是:

图 7：平面上的笛卡尔坐标网格在球面上出现了扭曲。虽然各个曲线之间依然保持垂直，但是各个网格方块的面积随着向北极点的靠近而收缩。

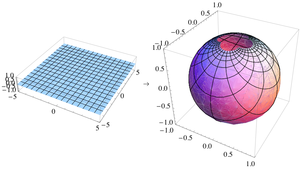
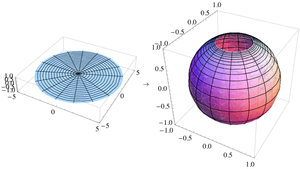
　　 $$P \in \mathbb{Q}^3 \Longleftrightarrow P' \in \mathbb{Q}^2~$$ 球极平面投影是共形的（保角），这意味着其能保持在映射前后曲线的相交角度不变（见图）。另一方面，球极平面投影不维持面积不变；一般来说，球面上的一个区域的面积不等于它投影到平面上之后的面积。坐标 (X, Y) 处的面积微元可以根据下式计算得到： $$\mathrm{d}A = \frac{4}{(1 + X^2 + Y^2)^2} \mathrm{d}X \, \mathrm{d}Y~$$ 沿着单位圆 $X^2 + Y^2 = 1$，在该单位圆上没有区域膨胀，比例因子为 1。接近 (0,0) 点的区域面积膨胀系数为 4，而接近无限远处的面积膨胀系数为无穷小。

图 8：平面上的极坐标网格在球面上出现了扭曲。虽然各个曲线之间依然保持垂直，但是各个网格扇区的面积随着向北极点的靠近而收缩。

　　在坐标 (X, Y) 处给出的度量可以根据下式计算得到： $$\frac{4}{(1 + X^2 + Y^2)^2} (\mathrm{d}X^2 + \mathrm{d}Y^2),~$$ 该公式最早出现于波恩哈德·黎曼(Bernhard Riemann)教授在几何基础的教授资格论文中，于 1854 年在哥廷根提交，标题为《论作为几何基础的假设》（Über die Hypothesen welche der Geometrie zu Grunde liegen）。

　　从球面到平面的映射不能既保角又保面积。如果要实现既保角又保面积，那么它将是一个局部等距图，并将保高斯曲率。而球面和平面有着不同的高斯曲率，所以球面到平面的映射不可能既保角又保面积。

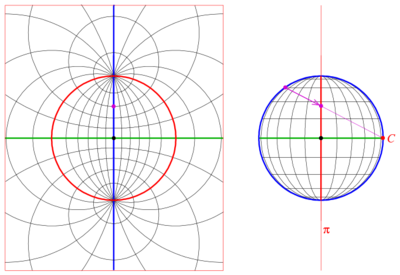
　　球面上不通过投影点的圆被投影为平面上的圆。球面上通过投影点的圆被投影为平面上的直线。这些直线有时被认为是通过无穷远点的圆，或半径为无穷大的圆。

　　平面上的所有直线，通过球极平面投影的逆变换为球面上的圆后，都相交于投影点。平面内不相交的平行线则变换为在投影点处相切的圆。而平面内的相交线变换为球面上相交于两个点的圆，其中一个交点为投影点。(类似的结论也适用于实射影平面，但与那里的相交关系有所不同。)

图 9：用不同的颜色表示球面上不同的恒向线

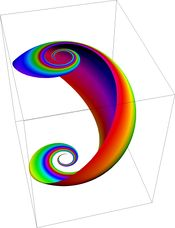
　　球面上的恒向线映射到平面上所得到的曲线具有以下形式： $$R = e^{\frac{\theta}{a}},~$$ 其中参数

　　 a 代表了恒向线的 “紧密度”。因此，球面上恒向线对应于平面上的对数螺线。这些螺旋与平面上的径向线等角相交，就像恒向线与球面上的经线等角相交一样。

　　球极平面投影以一种简单的对应方式与平面反演相关联。令球面上有 $P$ 点和 $Q$ 点，其在平面上的投影分别为 $P'$ 点和 $Q'$ 点。那么当且仅当 $P$ 点和 $Q$ 点关于赤道平面对称时，有 $P'$ 点和 $Q'$ 点互为赤道圆像中的逆像，

图 10

　　换句话说，如果：

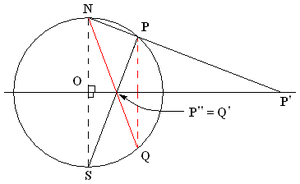
$P$ 是球面上除 “北极点 $N$” 及其对跖点 “南极点 $S$” 外的一个点，
$P'$ 是以 $N$ 为投影点时，$P$ 点球极平面投影，
$P''$ 是以 $S$ 为投影点时，$P$ 点球极平面投影，

　　那么称 $P'$ 点和 $P''$ 点关于单位圆相互逆像。 $$\triangle NOP' \sim \triangle P''OS \Longrightarrow OP' : ON = OS : OP'' \Longrightarrow OP' \cdot OP'' = r^2~$$

4. 乌尔夫网

图 11：乌尔夫网或立体网，用于手工绘制球极平面投影图

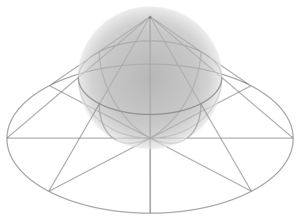
　　球极平面投影图可以由计算机根据上面给出的显式公式进行绘制。然而，当手工绘制时，这些公式是不实用的。作为替代，通常是使用专门为这项任务设计的方格纸。这种特殊的方格纸被称为立体网或乌尔夫网，以俄罗斯矿物学家乔治(尤里·维克托罗维奇)伍尔夫(George (Yuri Viktorovich) Wulff)的名字命名。[11]

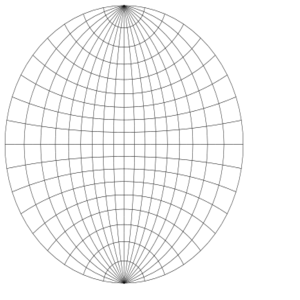
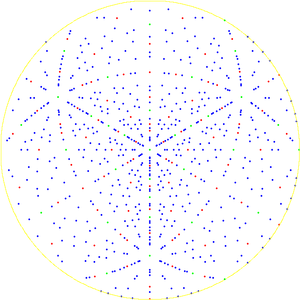
　　这里显示的乌尔夫网是以赤道上的点为中心的半球(如行星的东半球或西半球)纬线和经线网格的球极平面投影。

图 12：通过中心 C 及投影平面的球极平面投影生成一个乌尔夫网红色圆圈内的圆形网)

　　在图中，通过比较网格中心附近的网格扇区和最右边或最左边的网格扇区，可以看出球极平面投影的面积扭曲特性。这两个扇区在球面上有着相同的面积。但在平面上，后者的面积几乎是前者的四倍。如果网格变得更细，这个比例将收敛于 4。

　　在乌尔夫网，纬线和经线的图像以直角相交。这种正交性是立体投影的保角特性的结果。(然而，保角特性比该特性更强。并非所有保持纬线和经线正交性的投影都是保角的。)

图 13：在乌尔夫网上绘制点的步骤说明

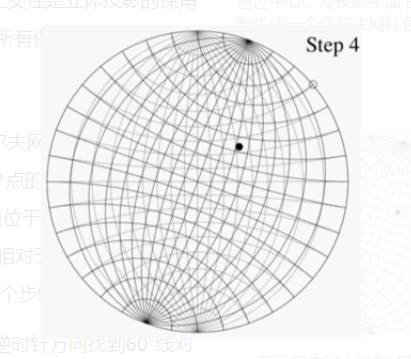
　　举一个使用乌尔夫网的例子，想象两个薄纸上的乌尔夫网副本，一个在另一个上面，对齐并保证它们的共同中心始终重合。令 $P$ 点的球面坐标为(140，60)，笛卡尔坐标为(0.321, 0.557, −0.766)。这一点位于从 $X$-轴正方向逆时针方向旋转 60° (或从 $Y$-轴正方向顺时针旋转 30° )并相对于 $z = 0$ 平面向下旋转 50°所得到的直线上。一旦知道这些角度，就有四个步骤来绘图 P 点:

使用图中所示间隔为 10°的网格线，从点(1, 0)沿逆时针方向找到 60°线对应的网格边缘点(或从点(1, 0)沿顺时针方向找到 30°线对应的网格边缘点)。
旋转上层的乌尔夫网，直到该点与下层乌尔夫网的(1, 0)点重合。
利用下层乌尔夫网的网格线，在上层乌尔夫网上标记出从该点向中心香菊 50°的点。
反向旋转上层乌尔夫网，使其与下层乌尔夫网对齐。那么步骤 3 中标记的点就是我们想要得到的投影。

　　要绘制角度不是类似于 60°和 50°的整数的其他点，必须在最近的网格线之间进行可视化的插值。间距小于 10°的网将有助于这些点的寻找。2°的间距是很常见的。

　　要根据球面上两点的球极平面投影图找到球面上两点之间的中心角，需将该图覆盖在乌尔夫网上，并围绕中心旋转该图，直到这两点位于子午线上或附近。然后通过计算子午线上的网格线来测量它们之间的角度。

$P_1$ 和 $P_2$ 两个点位于一个固定于乌尔夫网格原点的透明薄片上。
透明薄片旋转使得 $P_1$ 和 $P_2$ 和两个点位于同一条经线上，并由此得到两点之间的中心角.

图 14

图 15

5. 数学应用

5.1 复分析

图 16：复杂的平面及其上面的黎曼球

　　虽然任何体球极平面投影都会忽略球面上的一个点(投影点)，但是可以使用来自不同投影点的两个投影来映射整个球面。换句话说，球面可以被平面上的两个球极平面投影参数化(投影的逆)覆盖。可以通过参数化在球面上诱导相同的方向。它们一起将球面描述为一个定向曲面(或二维流形)。这种结构在复分析中具有特殊的意义。实平面上的点 $(X, Y)$ 可以用复数来表示 $\zeta = X + iY$。从北极点到赤道平面的球极平面投影是： $$\zeta = \frac{x + iy}{1 - z},~$$ $$(x, y, z) = \left( \frac{2 \operatorname{Re} \zeta}{1 + \bar{\zeta}\zeta }, \frac{2 \operatorname{Im} \zeta}{1 + \bar{\zeta}\zeta }, \frac{-1 + \bar{\zeta}\zeta }{1 + \bar{\zeta}\zeta } \right).~$$ 同样，令 $\xi = X - iY$ 作为另一个复坐标，那么函数： $$\xi = \frac{x - iy}{1 + z},~$$ $$(x, y, z) = \left( \frac{2 \operatorname{Re} \xi}{1 +\bar{\xi} \xi }, \frac{-2 \operatorname{Im} \xi}{1 + \bar{\xi}\xi }, \frac{1 -\bar{\xi} \xi}{1 + \bar{\xi}\xi } \right).~$$ 定义了从南极点到赤道平面的球极平面投影。$\zeta-$ 和 $\xi-$ 坐标之间的变换关系是 $\zeta = 1\xi$ 和 $\xi = 1\zeta$，当 $\zeta$ 趋向于 0 时，$\xi$ 趋向于无穷大，反之亦然。这有助于为复数提供一个简洁、有用的无穷概念，实际上也就是映射到黎曼球面的整个亚纯函数理论。单位球面上的标准度量与黎曼球面上的富比尼–施图迪度量是一致的。

5.2 线条和平面的可视化

图 17：面心立方晶体的八个<111>区域中的四个的菊池线动画。平面(带状线)以固定的角度相交。

　　三维空间中穿过原点的所有直线的集合形成了一个称为实射影平面的空间。这个空间很难想象，因为它不能嵌入到三维空间中。

　　然而，“几乎” 可以将其想象为一个圆盘。穿过原点的任何直线都与南半球面（$z \leq 0$）相交于一点，该点可以通过球极平面投影映射到圆盘上的一个点。水平线在沿着赤道的两个对跖点与南半球相交，这两个点中的任何一个都可以投影到圆盘上；可以理解，圆盘边界上的对跖点代表一条直线。所以穿过原点的任何一组线几乎可以完美地描绘成圆盘中的一组点。

　　此外，通过原点的每个平面与单位球面相交于一个大圆，称为平面的 “迹”。这个圆在球极平面投影下映射成一个圆。所以投影让我们把平面想象成圆盘中的圆弧。在计算机出现之前，有大圆的球极平面投影通常要画出需要使用横杆圆规的大半径圆弧。而电脑的出现使这项任务变得容易了很多。

　　与每个平面进一步相关联的是一条独特的线，称为平面的极线，它穿过原点并垂直于平面。这条线可以像穿过原点的任何线一样绘制成圆盘上的一个点。所以球极平面投影也让我们把平面想象成圆盘上的点。对于涉及许多平面的图，绘制它们的极线能得到比绘制它们的迹更不混乱的图像。

　　如图所示，这种构造可用于可视化晶体学和地质学中的晶向数据。

5.3 其他可视化

　　球极平面投影也应用于多胞体的可视化。在施莱格尔图中，一个 n-维正多胞体在 $R^{n+1}$ 投影到 n-维球面，然后用球极平面投影映射到 $R^n$。从 $R^{n+1}$ 降维到 $R^n$ 可以更容易地去想象和理解正多胞体。

5.4 算术几何

图 18：圆上的有理点在球极平面投影下与直线上的有理点对应。

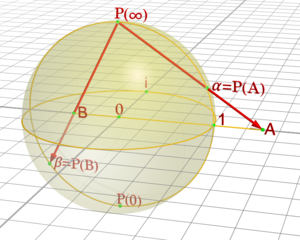
　　在初等算术几何中，单位圆的球极平面投影提供了一种描述所有原始勾股数的方法。具体地说，从北极点 $(0, 1)$ 到 $X$-轴的球极平面投影给出了单位圆上的有理数点 $(x, y)$（其中，$y \neq 1$）和 $x$-轴上有理数点之间一一对应的关系。如果 $(mn, 0)$ 是 $x$-轴上的一个有理数点，那么它的逆球极平面投影就是点： $$\left( \frac{2mn}{n^2 + m^2}, \frac{n^2 - m^2}{n^2 + m^2} \right)~$$ 其给出了勾股数的欧几里得公式。

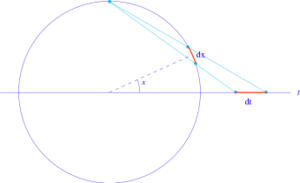
5.5 正切半角代换

图 19

　　三角函数对 $\left(\sin x, \cos x\right)$ 可以看做是单位圆的参数化。球极平面投影给出了一种单位圆的另一种参数化方法： $$\cos x = \frac{t^2 - 1}{t^2 + 1}, \quad \sin x = \frac{2t}{t^2 + 1}.~$$ 在这种新的参数化中，单位圆的长度微元 $dx$ 为： $$dx = \frac{2 \, dt}{t^2 + 1}.~$$ 这种代换有时可以简化涉及三角函数的积分。

6. 其他学科的应用

6.1 制图学

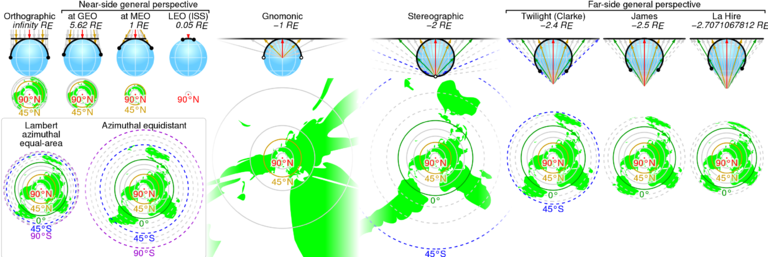
　　制图学的基本问题是从球面到平面的地图不能同时准确地表示角度和面积。一般来说，对于统计应用，优选保面积投影地图，而对于导航，优选保角(共形)投影地图。

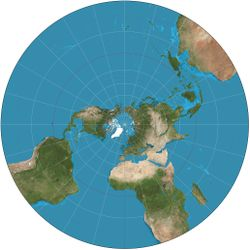
　　球极平面投影属于第二类。当投影以地球的北极点或南极点为中心时，它有额外的理想属性：它将经线映射为从原点呈射线状发出的直线，并将纬线映射为以原点为中心的圆。

南纬 30°以北的球极平面投影。每个网格为 15° 间隔。
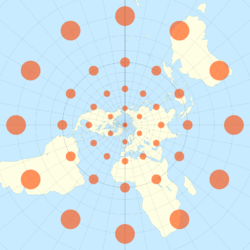
带有天梭变形指标的球极立体投影。

图 20

图 21

6.2 行星科学

　　球极平面投影是唯一能将球面上的所有圆映射为平面上的圆的投影。这一特性在以环形山为典型特征的行星测绘中很有价值。通过投影点的圆的集合具有无穷大的半径，因此退化为直线。

图 22：月球的球极平面投影，显示了北纬 60°以北的极地区域。圆形的陨石坑在这个投影中依然呈现圆形，不管它们是靠近极点还是地图的边缘。

6.3 晶体学

　　在晶体学中，晶体轴和面在三维空间中的取向是一个中心几何问题，例如在解释 $X$ 射线和电子衍射图案时。这些方向可以像上面的线和平面可视化部分一样可视化。也就是说，晶体轴和晶体平面的极点与北半球相交，并使用球极平面投影绘制。一个绘制了这些极点的图被称为极点图。

　　在电子衍射中，菊池线对表现为装饰晶格面迹线和埃瓦尔德球面之间交叉点的带，从而提供实验法获得晶体的球极平面投影的方法。菊池模型映射于互易空间中，[12]用于直接空间弯曲轮廓的条纹可见度图[13]，从而在透射电镜中作为探索晶体取向空间的路线图。

图 23：金刚石晶格在[111]方向上的一种晶体极点图。

6.4 地质学

图 24：在构造地质学中，利用下半球的球极立体投影来绘制平面和线性数据，此处以拥有滑擦面线理的断层平面为例进行展示。

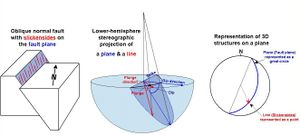
　　出于多种原因，结构地质学的研究人员关注平面和直线的方向。岩石的叶状结构是一种平面特征，通常包含一种称为线理的线性特征。类似地，断层平面是一个平面特征，可能包含线性特征，如滑擦面。

　　可以使用上述线和平面可视化部分的方法绘制这些不同比例的线和平面的方向。如同在晶体学中一样，平面通常由它们的极点绘制。与晶体学不同的，通常用南半球来代替北半球(因为所讨论的地质特征位于地表之下)。在这种情况下，球极平面投影通常被称为等角下半球投影。也会使用由朗伯方位等面积投影定义的等面积下半球投影，特别是当该图要进行后续的统计分析时，如密度等值线。

6.5 摄影

　　一些鱼眼镜头使用球极平面投影来捕捉广角视图。[14]与使用等面积投影的更传统的鱼眼镜头相比，靠近边缘的区域保持它们的形状，直线不太弯曲。然而，使用球极平面投影的鱼眼镜头通常制造成本更高。[15]图像重映射软件，例如 Panotools，允许自动将照片从等面积鱼眼重映射到球极平面投影。

　　球极平面投影已经用于绘制球形全景图。这种效果也被称为 “Little planet” (当投影中心是最低点时)或 “Tube”(当投影中心是最高点时)。[16]

　　相较于其他方位投影方法，使用球极平面投影的全景图映射的流行是由于该投影方法的保形性所导致的。[16]

图 25：2016 年 Wikimania 期间，意大利伦巴第省埃西诺拉里奥的米歇尔·维达尼(Michele Vedani)创作的《最后的晚餐》(the Last Supper)雕塑的球面全景球极立体投影。

7. 参考文献

　　 [1] ^Snyder (1993)..

　　 [2] ^According to (Snyder 1993), although he acknowledges he did not personally see it.

　　 [3] ^Snyder (1989)..

　　 [4] ^Brown, Lloyd Arnold : The story of maps, p.59..

　　 [5] ^According to (Elkins, 1988) who references Eckert, "Die Kartenwissenschaft", Berlin 1921, pp 121–123.

　　 [6] ^Timothy Feeman. 2002. "Portraits of the Earth: A Mathematician Looks at Maps". American Mathematical Society..

　　 [7] ^Cf. Apostol (1974) p. 17..

　　 [8] ^Gelfand，Minlos & Shapiro（1963）.

　　 [9] ^Cf. Pedoe (1988)..

　　 [10] ^Cf. Shafarevich (1995)..

　　 [11] ^Wulff, George, Untersuchungen im Gebiete der optischen Eigenschaften isomorpher Kristalle: Zeits. Krist.,36, 1–28 (1902).

　　 [12] ^M. von Heimendahl, W. Bell and G. Thomas (1964) Applications of Kikuchi line analyses in electron microscopy, J. Appl. Phys. 35:12, 3614–3616..

　　 [13] ^P. Fraundorf, Wentao Qin, P. Moeck and Eric Mandell (2005) Making sense of nanocrystal lattice fringes, J. Appl. Phys. 98:114308..

　　 [14] ^Samyang 8 mm f/3.5 Fisheye CS Archived 2011-06-29 at the Wayback Machine.

　　 [15] ^"Samyang 8 mm f/3.5 Aspherical IF MC Fish-eye". lenstip.com. Retrieved 2011-07-07..

　　 [16] ^German et al. (2007)..