普莱费尔公理（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　 在几何学中，普莱费尔公理是一个可以替代欧几里得第五公设（平行公设）的公理：

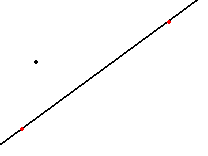
　　 在一个平面内，给定一条直线和一个不在该直线上的点，至多只能作一条经过该点且与已知直线平行的直线。\(^\text{[1]}\)

　　 它在欧几里得几何的语境下与欧几里得平行公设等价 \(^\text{[2]}\)，并以苏格兰数学家约翰·普莱费尔的名字命名。这里的 “至多一条” 这一限定就足够了，因为可以从前四条公理推导出：给定一条直线 $L$ 和一个不在 $L$ 上的点 $P$，至少存在一条平行线。推导过程如下：

1. 作垂线：利用公理和已建立的定理，可以作出一条通过点 $P$ 的直线，并且垂直于直线 $L$。
2. 作另一条垂线：再作一条通过点 $P$ 的直线，使其垂直于第一条垂线。
3. 得到平行线：由于平行线的定义（即根据第四条公理，内错角相等），这条第二条垂线与 $L$ 平行。

　　 该命题通常写作 “存在唯一一条平行线”。在欧几里得的《几何原本》中，两条直线被称为平行，当且仅当它们永不相交；而其他对平行线的刻画并未被使用。\(^\text{[3][4]}\)

　　 这一公理不仅用于欧几里得几何，也用于更广义的仿射几何研究中，在那里 “平行性” 的概念居于核心地位。在仿射几何的背景下，需要使用普莱费尔公理的更强形式（即将 “至多一条” 替换为 “唯一一条”），因为中性几何的公理体系缺乏提供存在性的证明。普莱费尔版的公理已如此广泛流行，以至于它常被称为欧几里得的平行公理 \(^\text{[5]}\)，尽管这并不是欧几里得本人提出的版本。

1. 历史

　　 普罗克洛斯（Proclus，公元 410–485 年）在其对欧几里得《几何原本》第一卷命题 31（I.31）的注释中，清楚地陈述了这一观点。\(^\text{[6]}\)

　　 1785 年，威廉·卢德拉姆将平行公理表述为：\(^\text{[7]}\)

　　 两条直线若在一点相交，则它们不能同时与第三条直线平行。

　　 这种简短的欧几里得平行性表述被普莱费尔采纳到其教材《几何学原本》（Elements of Geometry，1795）中，该书后来多次再版。他写道：\(^\text{[8]}\)

　　 两条相交的直线不能同时与同一条直线平行。

　　 普莱费尔承认卢德拉姆及其他人简化了欧几里得的表述。在后来的发展中，首先强调了两条直线的交点，随后将 “不能有两条平行线” 的说法，转化为 “通过给定点仅能作一条平行线”。\(^\text{[9]}\)

　　 1883 年，亚瑟·凯莱担任英国科学促进会会长，在会上发表演说时表达了如下观点：\(^\text{[10]}\)

　　 我个人认为，欧几里得第十二公理在普莱费尔的形式下，并不需要证明，而是我们关于空间这一概念的一部分，即经验中的物理空间，它构成了所有外在经验的底层表征。

　　 1899 年，大卫·希尔伯特撰写了《几何基础》\(^\text{[11]}\)，为欧几里得几何提供了一套新的公理体系。在讨论平行线时，他采用了普莱费尔形式的公理，而不是欧几里得原始的版本。\(^\text{[12]}\)

2. 与欧几里得第五公设的关系

　　 欧几里得的平行公设表述为：

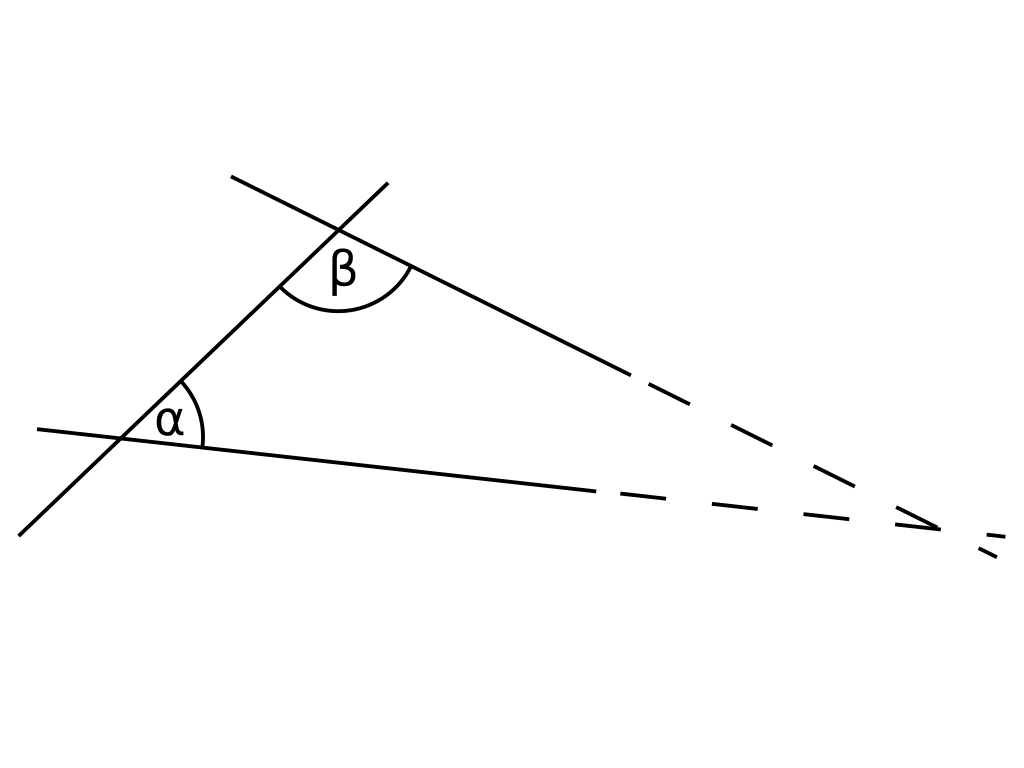
　　 如果一条线段与两条直线相交，并在同一侧形成的两个内角之和小于两个直角，那么这两条直线若无限延长，将在这一侧相交，即在角和小于两个直角的那一侧相交。\(^\text{[13]}\)

　　 与普莱费尔公理的简洁形式相比，这种表述的复杂性显然是导致人们在讨论平行公设时更倾向于引用普莱费尔公理的重要原因。

　　 在绝对几何的语境下，这两种表述是等价的，也就是说，在假设其余几何公理成立的前提下，可以用其中一个来证明另一个。这并不意味着二者在逻辑上严格等价（即仅通过形式逻辑推演就能相互证明），因为例如在椭圆几何的球面模型中，其中一个表述为真，而另一个则不成立。\(^\text{[14]}\) 而逻辑等价的命题必须在所有有解释的模型中具有相同的真值。

　　 以下的证明均假设绝对（中性）几何的所有公理均成立。

欧几里得第五公设蕴含普莱费尔公理

　　 最简单的证明方法是利用欧几里得定理（与第五公设等价），即三角形的内角和等于两个直角。给定一条直线 $\ell$ 和一个不在其上的点 $P$，先作一条经过 $P$ 的直线 $t$，使其垂直于 $\ell$，再在点 $P$ 作一条垂直于 $t$ 的直线。由于这条新直线不可能与 $\ell$ 相交并构成三角形（这一点在欧几里得《几何原本》第一卷命题 27 中有说明 \(^\text{[15]}\)），所以它与 $\ell$ 平行。由此可以看出，不存在其他平行线。若 $n$ 是另一条通过 $P$ 的直线，由于它不是垂线，因此与 $t$ 构成锐角，则满足第五公设的假设条件，因此 $n$ 必与 $\ell$ 相交。\(^\text{[16]}\)

普莱费尔公理蕴含欧几里得第五公设

　　 第五公设可以 “表面上” 通过以下方式证明：若欧几里得构造中的两条直线在内角和大于两个直角的一侧相交，那么将得到一个三角形，其中两个角的和大于两个直角，这与命题 1.17 矛盾。因此，它们必然在内角和小于两个直角的一侧相交。

　　 然而，这里假设了直线一定会相交。实际上我们证明的是：“若直线相交，则它们必定在内角和小于两个直角的一侧相交。” 普莱费尔公理通过事先假设 “给定点只有唯一一条平行线”（即 “垂线的垂线”）来保证直线一定相交。所有其他经过 $P$ 的直线都不是平行线，因此必然与 $\ell$ 相交。

三角形全等的重要性

　　 在缺乏三角形全等的情况下，普莱费尔公理与欧几里得第五公设的经典等价性就会失效。\(^\text{[17]}\) 这是通过构造一种几何体系来展示的：该体系重新定义了角度，使其满足希尔伯特的结合、次序与全等公理，但不满足边-角-边（SAS）全等。该几何模型符合经典的普莱费尔公理，却不符合欧几里得第五公设。

3. 平行性的传递性

　　 欧几里得的命题 30 表述为：“两条直线若各自平行于同一条第三直线，则它们彼此平行。” 奥古斯都·德·摩根指出 \(^\text{[18]}\)，这一命题在逻辑上等价于普莱费尔公理。这一观点后来由 T. L. Heath 于 1908 年转述 \(^\text{[19]}\)。德·摩根的论证如下：设 $X$ 为所有相交的不同直线对的集合，$Y$ 为所有各自平行于同一条直线的不同直线对的集合。若 $z$ 表示一对不同的直线，则以下命题

　　 $\forall z$, 如果 $z \in X$,那么 $z \notin Y$~

　　 就是普莱费尔公理（在德·摩根的术语中，即 “没有 $X$ 是 $Y$”）。其逻辑等价的逆否命题：

　　 $\forall z$ 如果 $z \in Y$,那么 $z \notin X$

　　 则是欧几里得 I.30，即平行性的传递性（“没有 $Y$ 是 $X$”）。

　　 更近代的表述方式则将其放在二元关系的语境下：在仿射几何中，平行关系被视为一种等价关系，这意味着一条直线被认为与自身平行。刘安迪 \(^\text{[20]}\) 写道：“设点 $P$ 不在直线 2 上。假设直线 1 和直线 3 都经过 $P$，并且平行于直线 2。根据传递性，直线 1 与直线 3 互相平行，因此它们不可能仅有 $P$ 这一个公共点。于是可以推出，它们实际上是同一条直线，这正是普莱费尔公理的内容。”

4. 注释

1. Playfair 1846，第 29 页
2. 更准确地说，是在绝对几何的语境中。
3. 《欧几里得原本》，第一卷，定义 23
4. Heath 1956，第 1 卷，第 190 页
5. 例如，Rafael Artzy (1965)《Linear Geometry》，第 202 页，Addison-Wesley 出版
6. Heath 1956，第 1 卷，第 220 页
7. William Ludlam (1785)《The Rudiments of Mathematics》，第 145 页，剑桥
8. Playfair 1846，第 11 页
9. Playfair 1846，第 291 页
10. William Barrett Frankland (1910)《Theories of Parallelism: A Historic Critique》，第 31 页，剑桥大学出版社
11. Hilbert, David (1990) [1971], 《几何基础》(Grundlagen der Geometrie)，Leo Unger 自德文第十版译（英文第二版），La Salle, IL: Open Court Publishing, ISBN 0-87548-164-7
12. Eves 1963，第 385–387 页
13. George Phillips (1826)《几何学原本》（包含欧几里得前六卷），第 3 页，Baldwin, Cradock, and Joy 出版
14. Henderson, David W.; Taimiņa, Daina (2005), 《Experiencing Geometry: Euclidean and Non-Euclidean with History》(第 3 版)，Upper Saddle River, NJ: Pearson Prentice Hall，第 139 页, ISBN 0-13-143748-8
15. 该论证假设的条件超出了证明结果所需。也存在一些关于平行线存在性的证明，不依赖于第五公设的等价形式。
16. Greenberg 1974，第 107 页
17. Brown, Elizabeth T.; Castner, Emily; Davis, Stephen; O’Shea, Edwin; Seryozhenkov, Edouard; Vargas, A. J. (2019-08-01). “On the equivalence of Playfair's axiom to the parallel postulate”. Journal of Geometry. 110 (2): 42. arXiv:1903.05233. doi:10.1007/s00022-019-0496-9. ISSN 1420-8997.
18. 《年鉴伴随文集》中的《欧几里得前六卷补充说明》，1849 年。
19. Heath 1956，第 1 卷，第 314 页
20. The College Mathematics Journal 42(5):372

参考文献

• Playfair, John (1846). Elements of Geometry. W. E. Dean.
• Eves, Howard (1963), A Survey of Geometry (Volume One), Boston: Allyn and Bacon
• Greenberg, Marvin Jay (1974), Euclidean and Non-Euclidean Geometries / Development and History, San Francisco: W\.H. Freeman, ISBN 0-7167-0454-4
• Heath, Thomas L. (1956). The Thirteen Books of Euclid's Elements（[影印版，原始出版：剑桥大学出版社，1908] 第二版）。纽约：Dover Publications.（三卷本）：ISBN 0-486-60088-2（卷一），ISBN 0-486-60089-0（卷二），ISBN 0-486-60090-4（卷三）。