欧拉角(综述)
贡献者: 待更新
本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。
欧拉角是由莱昂哈德·欧拉提出的三个角度,用于描述刚体相对于固定坐标系的方向。[1]
它们也可以表示物理学中运动参考系的方向,或三维线性代数中一般基的方向。
经典欧拉角通常采用倾斜角度的方式,其中零度表示垂直方向。后来,由彼得·古思里·泰特(Peter Guthrie Tait)和乔治·H·布赖恩(George H. Bryan)提出了替代形式,主要用于航空学和工程学中,其中零度表示水平位置。
1. 链式旋转等价性
欧拉角可以通过元素几何或旋转组合(即链式旋转)来定义。几何定义表明,三个元素旋转(绕坐标系的轴旋转)总是足够将物体定向到任何目标参考系。
这三个元素旋转可以是外在旋转(绕原始坐标系 xyz 轴旋转,假设坐标系保持静止),也可以是内在旋转(绕旋转坐标系 XYZ 轴旋转,该坐标系与运动体固连,在每次元素旋转后,物体相对于外部参考系的方向会发生变化)。
在下面的各节中,带有撇号标记的轴(例如,z″)表示元素旋转后的新轴。
欧拉角通常用 α、β、γ 或 ψ、θ、φ 来表示。不同的作者可能会使用不同的旋转轴集来定义欧拉角,或者使用不同的名称来表示相同的角度。因此,任何涉及欧拉角的讨论都应该首先明确它们的定义。
在不考虑使用两种不同约定来定义旋转轴(内在或外在)的情况下,旋转轴有十二种可能的旋转顺序,可以分为两组:
- 正确的欧拉角(\(z-x-z,x-y-x,y-z-y,z-y-z,x-z-x,y-x-y\))
- 泰特-布赖恩角(\(x-y-z,y-z-x,z-x-y,x-z-y,z-y-x,y-x-z\))。
泰特-布赖恩角也被称为卡尔丹角、航海角、航向、仰角和倾斜角,或偏航、俯仰和滚转角。有时,这两类旋转顺序都被称为 “欧拉角”。在这种情况下,第一组旋转顺序被称为正确的或经典的欧拉角。
2. 经典欧拉角
欧拉角是瑞士数学家莱昂哈德·欧拉(1707–1783)引入的三个角度,用于描述刚体相对于固定坐标系统的方向。
几何定义
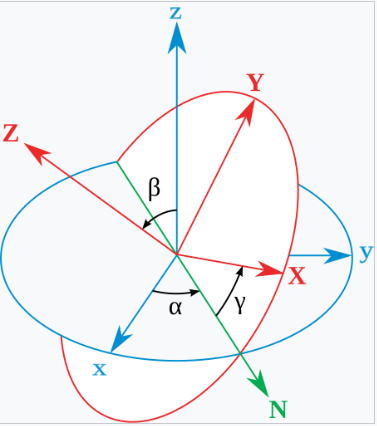
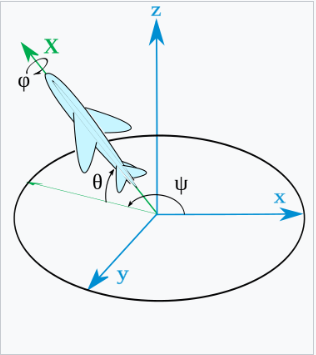
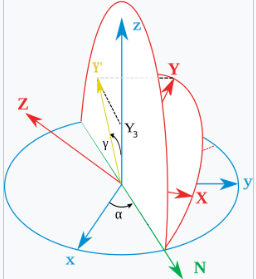
原始坐标系的轴表示为 \(x\)、\(y\)、\(z\),旋转后坐标系的轴表示为 \(X\)、\(Y\)、\(Z\)。几何定义(有时称为静态定义)首先定义节点线(N)为平面 \(xy\) 和 \(XY\) 的交线(也可以定义为轴 \(z\) 和 \(Z\) 的公垂线,然后表示为向量积 \(N = z \times Z\))。基于这个定义,三个欧拉角可以如下定义:
\(\alpha\)(或 \(\varphi\))是 \(x\) 轴与 \(N\) 轴之间的带符号角度(\(x\)-惯例——也可以定义为 \(y\) 轴与 \(N\) 轴之间的角度,称为 \(y\)-惯例)。 \(\beta\)(或 \(\theta\))是 \(z\) 轴与 \(Z\) 轴之间的角度。 \(\gamma\)(或 \(\psi\))是 \(N\) 轴与 \(X\) 轴之间的带符号角度(\(x\)-惯例)。
只有当两个参考系具有相同的手性时,才能定义这两个参考系之间的欧拉角。
内在旋转的约定
内在旋转是发生在附着于运动物体的坐标系统 $XYZ$ 的轴上的元素旋转。因此,它们在每次元素旋转后会改变其方向。$XYZ$ 系统会旋转,而 $xyz$ 系统保持固定。从 $XYZ$ 与 $xyz$ 初始重合开始,三个内在旋转的组合可以用来达到 $XYZ$ 的任何目标方向。
欧拉角可以通过内在旋转来定义。旋转后的坐标系 $XYZ$ 可以想象为最初与 $xyz$ 对齐,然后经历由欧拉角表示的三个元素旋转。其连续的方向可以表示如下:
- $x-y-z$ 或 $x_0-y_0-z_0$(初始)
- $x^\prime-y^\prime-z^\prime$ 或 $x_1-y_1-z_1$(第一次旋转后)
- $x"-y"-z"$ 或 $x_2-y_2-z_2$(第二次旋转后)
- $X-Y-Z$ 或 $x_3-y_3-z_3$(最终)
对于上述列出的旋转序列,节点线 $N$ 可以简单地定义为第一次元素旋转后 $X$ 的方向。因此,$N$ 可以简单地表示为 $x^\prime$。此外,由于第三次元素旋转是围绕 $Z$ 轴进行的,它不会改变 $Z$ 的方向。因此,$Z$ 与 $z"$ 重合。这使得我们可以简化欧拉角的定义如下:
- $\alpha$(或 $\varphi$)表示围绕 $z$ 轴的旋转,
- $\beta$(或 $\theta$)表示围绕 $x^\prime$ 轴的旋转,
- $\gamma$(或 $\psi$)表示围绕 $z"$ 轴的旋转。
外在旋转的约定
外在旋转是关于固定坐标系统 $xyz$ 轴的元素旋转 $XYZ$ 系统旋转,而 $xyz$ 系统保持不变。从 $XYZ$ 与 $xyz$ 重合开始,通过三次外在旋转的组合可以实现任何目标方向。欧拉角或泰特–布莱恩角($\alpha,\beta,\gamma$)表示这些元素旋转的幅度。例如,目标方向可以按以下步骤实现(注意欧拉角应用的顺序是反向的):
- $XYZ$ 系统绕 $z$ 轴旋转角度 $\gamma$。此时 $X$ 轴与 $x$ 轴的夹角为 γ。
- $XYZ$ 系统再次旋转,这次绕 $x$ 轴旋转角度 $\beta$。此时 $Z$ 轴与 $z$ 轴的夹角为 $\beta$。
- $XYZ$ 系统第三次旋转,绕 $z$ 轴再旋转角度 $\alpha$。
总之,三次元素旋转依次发生在 $z,x$ 和 $z$ 轴上。实际上,这个旋转序列通常表示为 $z-x-z$(或 3-1-3)。与欧拉角和泰特–布莱恩角相关的旋转轴集合通常使用这种符号表示(具体细节请参见上文)。
如果每一步旋转都作用于旋转坐标系统 $XYZ$,那么该旋转为内在旋转($Z-X^\prime-Z"$)。内在旋转也可以表示为 3-1-3。
符号、范围和约定
角度通常按照右手法则定义。即,当角度表示的旋转在沿轴正方向观察时呈顺时针方向时,其值为正;当旋转呈逆时针方向时,值为负。相反的约定(左手法则)较少采用。
关于范围(使用区间表示法):
- 对于 $\alpha$ 和 $\gamma$,范围定义为模 $2\pi$ 弧度。例如,一个有效的范围可以是 $[ -\pi,\pi]$。
- 对于 $\beta$,范围覆盖π弧度(但不能称其为模 $\pi$ 的)。例如,它可以是 $[0,\pi]$ 或 $[-\pi/2,\pi/2]$。
角度 $\alpha,\beta$ 和 $\gamma$ 唯一确定,除了一个特殊情况,即当 $xy$ 平面和 $XY$ 平面重合时,即当 $z$ 轴和 $Z$ 轴方向相同或相反时。实际上,如果 $z$ 轴和 $Z$ 轴方向相同,则 $\beta =0$,只有 $(\alpha+\gamma)$ 被唯一确定(而不是各自的值);同样,如果 $z$ 轴和 $Z$ 轴方向相反,则 $\beta=\pi$,只有 $(\alpha-\gamma)$ 被唯一确定(而不是各自的值)。这些模糊性在应用中被称为 “万向节锁”。
有六种选择旋转轴的方式来确定欧拉角。在所有情况下,第一和第三个旋转轴是相同的。这六种可能的顺序是:
- $z_1-x'-z_2"$(内旋转)或 $z_2-x-z_1$(外旋转)
- $x_1-y'-x_2"$(内旋转)或 $x_2-y-x_1$(外旋转)
- $y_1-z'-y_2"$(内旋转)或 $y_2-z-y_1$(外旋转)
- $z_1-y'-z_2"$(内旋转)或 $z_2-y-z_1$(外旋转)
- $x_1-z'-x_2"$(内旋转)或 $x_2-z-x_1$(外旋转)
- $y_1-x'-y_2"$(内旋转)或 $y_2-x-y_1$(外旋转)
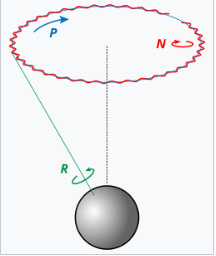
进动、章动和内旋转
进动、章动和内旋转(自旋)被定义为通过改变其中一个欧拉角,同时保持其他两个角度不变所得到的运动。这些运动不是通过外部坐标系来表示,也不是通过与物体共同旋转的坐标系来表示,而是两者的混合。它们构成了一个混合轴旋转系统,其中第一个角度使节点线绕外部轴 $z$ 旋转,第二个角度绕节点线 $N$ 旋转,第三个角度则是绕 $Z$ 轴的内旋转,$Z$ 轴是一个固定在物体上的轴,随着物体的运动而改变。
静态定义意味着:
- $\alpha$(进动)表示绕 $z$ 轴的旋转,
- $\beta$(章动)表示绕 $N$ 或 $x'$ 轴的旋转,
- $\gamma$(内旋转)表示绕 $Z$ 或 $z"$ 轴的旋转。
如果 $\beta$ 为零,则没有绕 $N$ 轴的旋转。因此 $Z$ 与 $z$ 重合,$\alpha$ 和 $\gamma$ 表示绕同一轴($z$)的旋转,最终的方向可以通过绕 $z$ 轴的单一旋转来获得,旋转角度等于 $\alpha+\gamma$。
例如,考虑陀螺仪。陀螺仪绕其自身的对称轴旋转;这对应于它的内旋转。它还绕其支撑轴旋转,质心绕支撑轴做轨道运动;这种旋转是进动。最后,陀螺仪可能会上下摆动;这个倾斜角度就是章动角度。类似的例子也可以用地球的运动来说明。
虽然所有三种运动都可以通过某个坐标系中的旋转算子表示,并且这些算子的系数是常数,但它们不能同时通过这些算子来表示。给定一个参考框架,最多只有一个旋转可以没有系数。一般来说,只有进动可以在空间基底中作为矩阵来表达,而不依赖于其他角度。
这些运动也表现得像一个万向节系统。给定一组框架,每个框架都能根据一个角度相对于前一个框架旋转,就像万向节一样,那么将会存在一个外部固定框架,一个最终框架和两个中间框架,这些中间框架被称为 “中间框架”。这两个中间框架就像两个万向节环,使得最后一个框架能够达到空间中的任何方向。
3. 泰特–布莱恩角
第二种形式主义称为泰特–布莱恩角(Tait–Bryan angles),以苏格兰数学物理学家彼得·古思里·泰特(Peter Guthrie Tait,1831–1901)和英国应用数学家乔治·H·布莱恩(George H. Bryan,1864–1928)的名字命名。它是航空航天应用中通常使用的约定,其中零度仰角表示水平姿态。泰特–布莱恩角表示飞机相对于世界坐标系的方向。当涉及到其他类型的飞行器时,可能采用不同的轴约定。
定义
泰特–布莱恩角的定义和符号与上述的正欧拉角(几何定义、内旋转定义、外旋转定义)类似。唯一的区别是,泰特–布莱恩角表示绕三个不同的轴旋转(例如 $x-y-z$,或 $x-y'-z"$),而正欧拉角在第一和第三个元素旋转时使用相同的轴(例如 $z-x-z$,或 $x-y'-z"$)。
这意味着在几何构造中,节点线的定义不同。在正欧拉角的情况下,节点线被定义为两个同类笛卡尔平面的交线(当欧拉角为零时,平面平行;例如 $xy$ 和 $XY$)。而在泰特–布莱恩角的情况下,节点线被定义为两个非同类平面的交线(当欧拉角为零时,平面垂直;例如 $xy$ 和 $YZ$)。
约定
三种基本旋转可以发生在原始坐标系的轴上,该坐标系保持不动(外旋转),也可以发生在旋转坐标系的轴上,旋转坐标系在每次基本旋转后都会改变其方向(内旋转)。
对于泰特–布莱恩角,选择旋转轴有六种可能。六种可能的顺序如下:
- $x-y'-z"$(内旋转)或 $z-y-x$(外旋转)
- $y-z'-x"$(内旋转)或 $x-z-y$(外旋转)
- $z-x'-y"$(内旋转)或 $y-x-z$(外旋转)
- $x-z'-y"$(内旋转)或 $y-z-x$(外旋转)
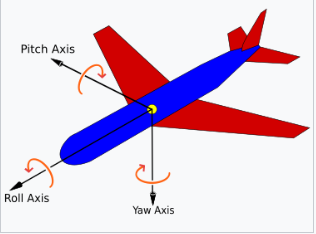
- $z-y'-x"$(内旋转)或 $x-y-z$(外旋转):内旋转通常称为:偏航(yaw)、俯仰(pitch)和滚转(roll)
- $y-x'-z"$(内旋转)或 $z-x-y$(外旋转)
符号和范围
泰特–布莱恩约定在工程中被广泛应用,具有不同的目的。实际中有多种选择移动轴和固定轴的轴约定,这些约定决定了角度的符号。因此,在每种情况下必须仔细研究符号。
角度 $\Psi$ 和 $\varphi$ 的范围覆盖 $2\pi$ 弧度。对于 $\theta$,范围覆盖 $\pi$ 弧度。
替代名称
这些角度通常在外部参考框架中取一个(航向角、方位角),在内旋转的移动框架中取一个(滚转角),并在一个中间框架中取一个,表示相对于水平面的仰角或倾斜角,这对于这个目的来说等同于节点线。
作为链式旋转
对于一架飞机,如果按照正确的顺序并从与参考框架重合的框架开始,可以通过绕其主轴的三次旋转来获得这些角度。
- 进动(yaw)得到方位角,
- 俯仰(pitch)得到仰角,
- 滚转(roll)得到滚转角。
因此,在航空航天领域,它们有时被称为偏航角、俯仰角和滚转角。请注意,如果旋转按照其他顺序应用,或如果飞机的轴线不从与参考框架等效的位置开始,则这种方法将无法奏效。
泰特–布莱恩角,按照 $z-y'-x"$(内旋转)约定,也被称为航海角,因为它们可以用来描述船只或飞机的方向,或者被称为卡尔达诺角,以纪念意大利数学家和物理学家杰罗拉莫·卡尔达诺(Gerolamo Cardano),他首次详细描述了卡尔达诺悬挂系统和卡尔达诺接头。
4. 给定坐标系的角度
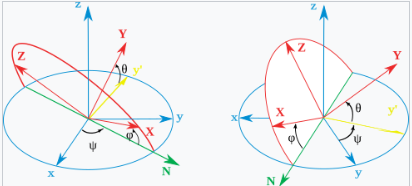
一个常见的问题是求给定坐标系的欧拉角。获得欧拉角的最快方法是将三个给定的向量写成矩阵的列,并将其与理论矩阵的表达式进行比较(见后面的矩阵表格)。因此,可以计算出三个欧拉角。然而,使用基本几何而不依赖矩阵代数也可以得到相同的结果。这里我们展示了两种最常用的约定的结果:$ZXZ$ 用于正欧拉角,$ZYX$ 用于泰特–布莱恩角。请注意,任何其他约定都可以通过更改轴的名称来获得。
正欧拉角
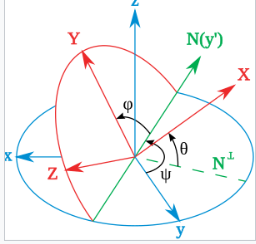
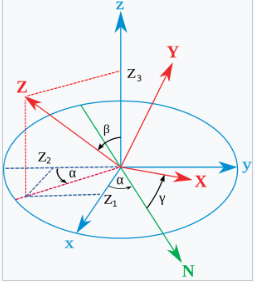
假设一个坐标系,单位向量 (X, Y, Z) 由其坐标给出,如主图所示,可以得出: \[ \cos\left(\beta\right) = Z_3.~ \] 由于 \[ \sin^2 x = 1 - \cos^2 x,~ \] 对于 \( 0 < \beta < \pi \),我们有: \[ \sin\left(\beta\right) = \sqrt{1 - Z_3^2}.~ \] 由于 \( Z_2 \) 是单位向量的双重投影, \[ \cos\left(\alpha\right) \cdot \sin\left(\beta\right) = -Z_2,~ \] 所以 \[ \cos\left(\alpha\right) = -Z_2/\sqrt{1 - Z_3^2}.~ \] 对于 \( Y_3 \),我们有类似的构造,首先将其投影到由轴 z 和节点线定义的平面上。由于两个平面之间的角度是 \( \pi/2 - \beta \),并且 \(\cos\left(\pi/2 - \beta\right) = \sin\left(\beta\right) ,\) 这导致: \[ \sin\left(\beta\right) \cdot \cos\left(\gamma\right) = Y_3,~ \] 所以 \[ \cos\left(\gamma\right) = Y_3/\sqrt{1 - Z_3^2}.~ \] 最后,使用反余弦函数,我们可以得到: \[ \alpha = \arccos\left(-Z_2/\sqrt{1 - Z_3^2}\right),~ \]
\[ \beta = \arccos\left(Z_3\right) ,~ \]
\[ \gamma = \arccos\left(Y_3/\sqrt{1 - Z_3^2}\right).~ \]
泰特–布莱恩角
假设一个坐标系,单位向量 (X, Y, Z) 由其坐标给出,如此新图所示(注意角度 \( \theta \) 是负的),可以得出: \[ \sin\left(\theta\right) = -X_3.~ \] 如同之前的推导, \[ \cos^2 x = 1 - \sin^2 x,~ \] 对于 \( -\pi/2 < \theta < \pi/2 \),我们有: \[ \cos\left(\theta\right) = \sqrt{1 - X_3^2}.~ \] 与前面的推导类似: \[ \sin\left(\psi\right) = X_2/\sqrt{1 - X_3^2},~ \]
\[ \sin\left(\phi\right) = Y_3/\sqrt{1 - X_3^2}.~ \] 寻找与前面类似的表达式: \[ \psi = \arcsin\left(X_2/\sqrt{1 - X_3^2}\right),~ \]
\[ \theta = \arcsin\left(-X_3\right) ,~ \]
\[ \phi = \arcsin\left(Y_3/\sqrt{1 - X_3^2}\right).~ \]
最后的备注
请注意,反正弦和反余弦函数会为其参数提供两个可能的值。在这个几何描述中,只有一个解是有效的。当欧拉角定义为旋转序列时,所有解都可能有效,但只有一个解位于角度范围内。这是因为,如果范围没有事先定义,那么到达目标坐标系的旋转序列不是唯一的。[2]
为了计算的方便,使用 \( \text{atan2}(y, x) \) 来表示角度可能会很有用。例如,在正欧拉角的情况下: \[ \alpha = \operatorname{atan2}(Z_1, -Z_2),~ \]
\[ \gamma = \operatorname{atan2}(X_3, Y_3).~ \]
5. 转换为其他方向表示法
主条目:三维旋转公式 § 旋转公式之间的转换公式
欧拉角是一种表示方向的方法。还有其他方法,可以在不同的约定之间进行转换。描述三维欧几里得空间中的方向总是需要三个参数。它们可以通过多种方式给出,欧拉角是其中之一;有关其他方法,请参见 SO(3)的图表。
最常见的方向表示法有旋转矩阵、轴角表示法和四元数(也称为欧拉–罗德里格斯参数),它们提供了另一种表示三维旋转的机制。这等同于特殊酉群的描述。
将三维旋转表示为单位四元数而不是矩阵有一些优点:
- 连接旋转的计算更快,数值更稳定。
- 提取旋转角度和旋转轴更简单。
- 插值更直观。例如,参考球面线性插值(slerp)。
- 四元数不像欧拉角那样会遇到万向节锁死(gimbal lock)问题。
无论如何,旋转矩阵的计算是获得其他两种表示法的第一步。
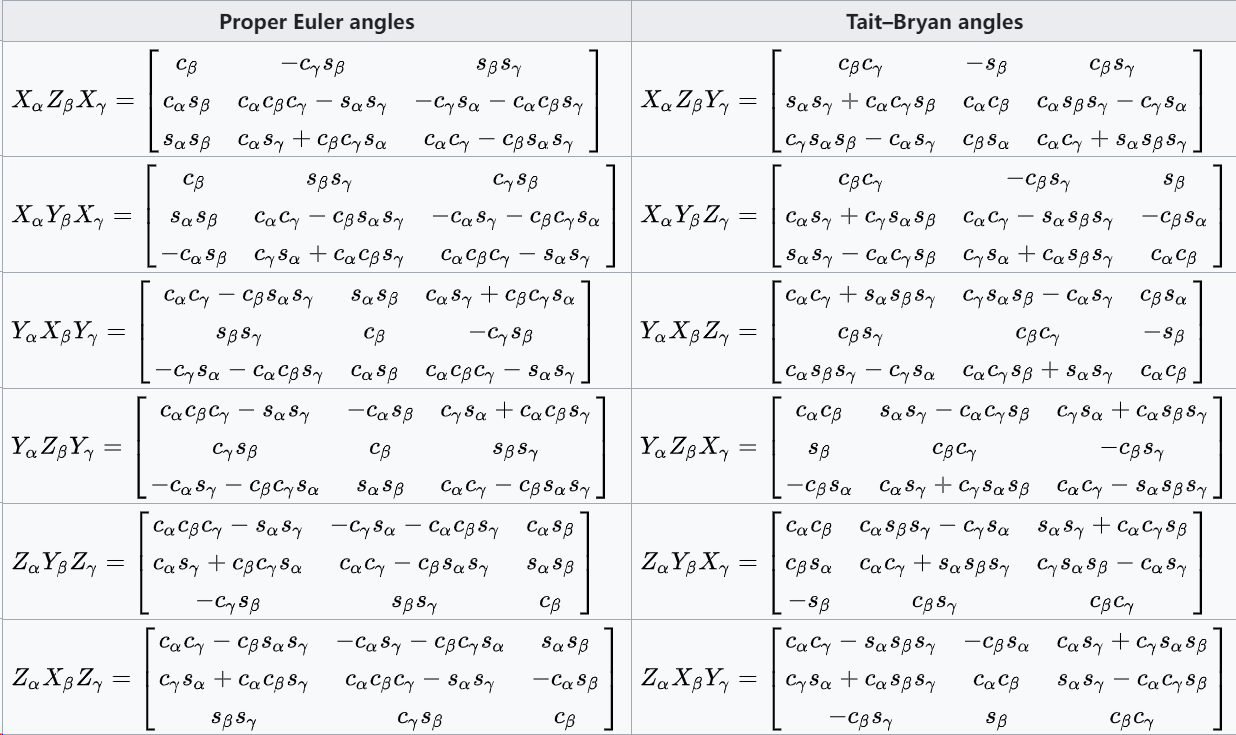
旋转矩阵
任何方向都可以通过从已知标准方向开始,组合三个基本旋转来实现。等效地,任何旋转矩阵 \( R \) 都可以分解为三个基本旋转矩阵的乘积。例如: \[ R = X(\alpha) Y(\beta) Z(\gamma)~ \] 这是一个旋转矩阵,可以用来表示关于 $z,y,x$ 轴的外旋转的组合(按此顺序),或者表示关于 $x-y'-z"$ 轴的内旋转的组合(按此顺序)。然而,基本旋转矩阵 \( X \)、\( Y \)、\( Z \) 的定义以及它们的乘法顺序取决于用户对旋转矩阵和欧拉角定义的选择(例如,参见旋转矩阵定义中的歧义)。不幸的是,不同的约定集在不同的上下文中被用户采用。以下表格是根据这一约定集构建的:
- 每个矩阵都意味着通过左乘列向量 \[ \begin{bmatrix} x \\ y \\ z \end{bmatrix}~ \] (参见旋转矩阵定义中的歧义)
- 每个矩阵都表示一个主动旋转(组成矩阵和被组成矩阵假定作用于在初始固定参考系中定义的向量坐标,并给出旋转后向量在同一参考系中的坐标)。
- 每个矩阵主要表示内旋转的组合(绕旋转参考系的轴旋转),其次表示外旋转的组合(三个外旋转的乘积,表示通过三个真正的基本矩阵的乘法按相反顺序构造得到 \( R \) 矩阵)。 采用右手坐标系,并使用右手定则来确定角度 \( \alpha \)、\( \beta \)、\( \gamma \) 的符号。
为了简化,以下矩阵乘积表使用了以下命名法:
- \( X \)、\( Y \)、\( Z \) 是表示绕固定坐标系的 \( x \)、\( y \)、\( z \) 轴旋转的基本矩阵(例如,\( X_\alpha \) 表示绕 \( x \) 轴旋转角度 \( \alpha \))。
- \( s \) 和 \( c \) 分别表示正弦和余弦(例如,\( s_\alpha \) 表示 \( \alpha \) 的正弦)。
这些表格结果可以在许多教科书中找到。[3] 对于每一列,最后一行表示最常用的约定。
要更改被动旋转的公式(或找到反向主动旋转),只需转置矩阵(此时每个矩阵将初始坐标系中的向量坐标转换为在旋转参考系中测量的相同向量的坐标;相同的旋转轴,相同的角度,但现在是坐标系旋转,而不是向量旋转)。
下表包含了从旋转矩阵元素 \( R \) 中得到的角度 \(\alpha\),\(\beta\) 和 \(\gamma\) 的公式。[4]
6. 性质
欧拉角在 SO(3)上形成一个图表,SO(3)是三维空间中旋转的特殊正交群。该图表在除了β = 0 处沿着极坐标样式的奇点外是光滑的。有关 SO(3)的更完整处理,请参见 SO(3)的图表。
旋转空间通常被称为 “旋转的超球面”,尽管这是一个误称:群 Spin(3)与超球面 S3 等距,但旋转空间 SO(3)实际上与实射影空间 RP3 等距,后者是超球面的一个二重商空间。这种二对一的模糊性是物理中自旋的数学来源。
类似的三角分解也适用于 SU(2),这是复二维空间中旋转的特殊酉群,区别在于β的范围从 0 到 2π。这些角度也被称为欧拉角。
SO(3)在欧拉角下的 Haar 测度由 SO(3)的 Hopf 角参数化给出:\(dV \propto \sin \beta \cdot d\alpha \cdot d\beta \cdot d\gamma,\) 其中(\(\beta, \alpha\))参数化 \(S^2\),即旋转轴的空间。
例如,要生成均匀随机的方向,可以让 \(\alpha\) 和 \(\gamma\) 在 0 到 2π之间均匀分布,\(z\) 在-1 到 1 之间均匀分布,然后让 \(\beta = \arccos\left(z\right) \)。
几何代数
欧拉角和旋转的其他性质通常可以通过几何代数来找到,这是一种更高层次的抽象,其中四元数是一个偶代数。几何代数中的主要工具是旋转算子(rotor),表示为:\(\mathbf{R} = [ \cos\left(\theta / 2\right) - I\mathbf{u} \sin\left(\theta / 2\right) ],\) 其中,\(\theta\) 是旋转角度,\(\mathbf{u}\) 是旋转轴(单位向量),\(\mathbf{I}\) 是伪标量(\(\mathbb{R}^3\) 中的三向量)。
更高维度
在高于三维的空间中,可以定义类似于欧拉角的参数。[6] [7][来源不可靠?] 在四维及以上的空间中,“绕轴旋转” 的概念失去意义,取而代之的是 “平面内旋转”。表示 SO(n)群所需的欧拉角数量是 \( \frac{n(n - 1)}{2} \),等于在 n 维欧几里得空间中包含两个不同坐标轴的平面数量。
在 SO(4)中,旋转矩阵由两个单位四元数定义,因此具有六个自由度,每个四元数提供三个自由度。
7. 应用
车辆和运动框架
欧拉角相较于其他姿态描述方法的主要优势在于它们可以直接通过安装在车辆中的万向节进行测量。由于陀螺仪保持其旋转轴不变,因此在陀螺框架中测量的角度与在实验室框架中测量的角度是等效的。因此,陀螺仪被用来确定运动航天器的实际姿态,欧拉角是可以直接测量的。单一万向节无法读取固有旋转角度,因此航天器中必须有多个万向节。通常至少有三个万向节以确保冗余。此外,这也与机械工程中著名的万向节锁问题有关。[8]
在研究刚体时,通常称 xyz 系统为空间坐标系,XYZ 系统为身体坐标系。空间坐标被视为静止的,而身体坐标则被视为嵌入在运动的刚体中的。涉及加速度、角加速度、角速度、角动量和动能的计算通常在身体坐标系中最为简便,因为此时转动惯量张量不会随时间变化。如果还对刚体的转动惯量张量进行对角化(该张量有九个分量,其中六个是独立的),则可以得到一组坐标(称为主轴),在这些坐标系中转动惯量张量只有三个分量。
刚体的角速度在运动框架下使用欧拉角时具有简洁的形式。同时,欧拉刚体方程也变得更为简化,因为在该框架下,转动惯量张量是恒定的。
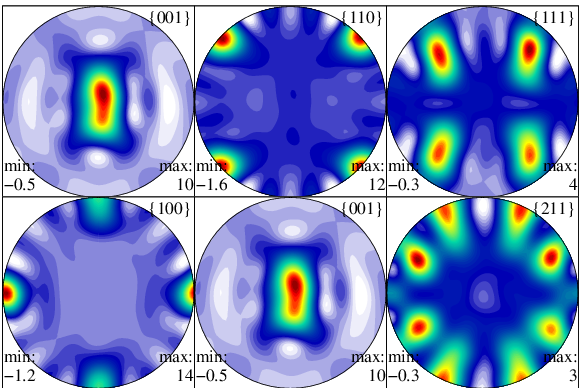
晶体学取向
在材料科学中,晶体学取向(或优选取向)可以使用欧拉角进行描述。在取向分析中,欧拉角提供了单个晶粒在多晶材料中取向的数学表示,从而实现了对宏观材料的定量描述。[10]
欧拉角的最常见定义来自于 Bunge,并且对应于 ZXZ 约定。然而,需要注意的是,这一应用通常涉及张量量的轴变换,即被动旋转。因此,Bunge 欧拉角所对应的矩阵是上述表格中矩阵的转置。[11]
其他
欧拉角,通常采用泰特–布赖恩约定,也在机器人学中用于描述腕部的自由度。在电子稳定控制中也以类似的方式应用。
炮火控制系统需要对炮口角度(方位角和仰角)进行修正,以补偿甲板倾斜(俯仰和滚转)。在传统系统中,具有垂直旋转轴的稳定陀螺仪用于修正甲板倾斜,并稳定光学瞄准镜和雷达天线。然而,炮管的指向与视线方向不同,以预测目标的运动以及由于重力导致的弹道下落等因素。炮架随着甲板平面滚转和俯仰,但也需要稳定。炮火指令包括根据垂直陀螺仪数据计算的角度,这些计算涉及欧拉角。
欧拉角还广泛应用于角动量的量子力学。在量子力学中,SO(3)表示的显式描述对计算至关重要,几乎所有的相关工作都是通过欧拉角来完成的。在量子力学的早期历史中,当物理学家和化学家对抽象的群论方法(称为 “群论疫病”)产生强烈反感时,依赖于欧拉角也是基础理论工作中不可或缺的部分。
许多移动计算设备包含加速度计,可以确定这些设备相对于地球重力吸引的欧拉角。这些设备用于诸如游戏、气泡水平仪仿真和万花筒等应用。[citation needed]
8. 另见
- 3D 投影
- 轴-角表示法
- 四元数与欧拉角的转换
- 达文波链式旋转
- 欧拉旋转定理
- 万向节锁
- 四元数
- 四元数与空间旋转
- 三维中的旋转形式
- 球坐标系
9. 参考文献
- Novi Commentarii academiae scientiarum Petropolitanae 20, 1776, 第 189–207 页 (E478) PDF
- Gregory G. Slabaugh, 《从旋转矩阵计算欧拉角》
- 例如:Roithmayr, Carlos M.; Hodges, Dewey H. (2016)。Dynamics: Theory and Application of Kane's Method(第 1 版)。剑桥大学出版社。ISBN 978-1107005693。
- Henderson, D. M. (1977 年 6 月 9 日)。“空间航天飞机分析的欧拉角、四元数和变换矩阵”(技术报告)。NASA,第 12–24 页。
- Yershova, A.; Jain, S.; Lavalle, S. M.; Mitchell, J. C. (2010)。“使用 Hopf 纤维化生成 SO(3)上的均匀增量网格”。《国际机器人研究杂志》,29(7)。第 8 节 – Hopf 参数化的推导。doi:10.1177/0278364909352700。PMC 2896220。PMID 20607113。
- Hoffman, D. K. (1972),*“欧拉角向 N 维正交矩阵的推广”*,[J. Math. Phys. 13, 528–533],doi:10.1063/1.1666011
- 意大利语)“欧拉角向 n 维实空间的推广”
- 欧拉角与卡尔丹悬挂之间的关系在以下教材的第 11.7 章中有所解释:U. Krey, A. Owen,《基础理论物理学 – 简明概述》,纽约、伦敦、柏林、海德堡,Springer(2007)。
- Liss KD, Bartels A, Schreyer A, Clemens H (2003)。“高能 X 射线:材料科学和物理学中先进大宗研究的工具”。《纹理与微观结构》,35 (3/4): 219–252。doi:10.1080/07303300310001634952。
- Kocks, U.F.; Tomé, C.N.; Wenk, H.-R. (2000),“纹理与各向异性:多晶体中的优选取向及其对材料性质的影响”,剑桥,ISBN 978-0-521-79420-6。
- Bunge, H. (1993),“材料科学中的纹理分析:数学方法”,Cuvillier Verlag,ASIN B0014XV9HU。
10. 参考书目
- Biedenharn, L. C.; Louck, J. D. (1981),Angular Momentum in Quantum Physics,雷丁,马萨诸塞州:Addison–Wesley,ISBN 978-0-201-13507-7
- Goldstein, Herbert (1980),Classical Mechanics(第 2 版),雷丁,马萨诸塞州:Addison–Wesley,ISBN 978-0-201-02918-5
- Gray, Andrew (1918),A Treatise on Gyrostatics and Rotational Motion,伦敦:Macmillan(2007 年出版),ISBN 978-1-4212-5592-7
- Rose, M. E. (1957),Elementary Theory of Angular Momentum,纽约,纽约州:John Wiley & Sons(1995 年出版),ISBN 978-0-486-68480-2
- Symon, Keith (1971),Mechanics,雷丁,马萨诸塞州:Addison-Wesley,ISBN 978-0-201-07392-8
- Landau, L.D.; Lifshitz, E. M. (1996),Mechanics(第 3 版),牛津:Butterworth-Heinemann,ISBN 978-0-7506-2896-9
11. 参考资料
- "Euler angles", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Euler Angles". MathWorld.
- David Eberly. Euler Angle Formulas, Geometric Tools
- 一份关于欧拉角的互动教程,网址:[https://www.mecademic.com/en/how-is-orientation-in-space-represented-with-euler-angles](https://www.mecademic.com/en/how-is-orientation-in-space-represented-with-euler-angles)
- EulerAngles – 一款 iOS 应用程序,用于以 3D 方式可视化与欧拉角相关的三种旋转
- Orientation Library – "orilib",一个用于旋转/取向操作的程序库,包含晶体取向的特殊工具
- 在线工具用于转换旋转矩阵,网址:[rotation converter](https://www.rotationconverter.com)(数值转换)
- 在线工具用于转换符号旋转矩阵(已不再更新,但仍可通过 Wayback Machine 访问):[symbolic rotation converter](https://web.archive.org/web/...)
- Rotation, Reflection, and Frame Change: Orthogonal tensors in computational engineering mechanics, IOP Publishing
- Euler Angles, Quaternions, and Transformation Matrices for Space Shuttle Analysis, NASA