贡献者: _Eden_
让我们回顾流体力学的动量守恒方程:
\begin{equation}
\rho \frac{\partial \boldsymbol{\mathbf{u}} }{\partial t}+\rho( \boldsymbol{\mathbf{u}} \cdot \nabla) \boldsymbol{\mathbf{u}} =\rho \boldsymbol{\mathbf{g}} +\nabla\cdot \overleftrightarrow { \boldsymbol{\mathbf{T}} }~.
\end{equation}
为了进一步解这个方程,我们需要知道应力张量 $T_{ij}$ 的具体形式。$T_{ij}$ 表示在法线为 $x_i$ 方向的单位面元上,面外对面内的面力的 $x_j$ 分量,而且是二阶对称张量(为了保证角动量守恒),那么它有怎样的性质呢?
在下面的讨论中我们将假设我们讨论的流体是牛顿流体:流体的应力和流体的速度梯度有线性关系,也就是服从广义胡克定律的关系。这当然是不正确的,因为实际问题中,当形变特别大时,有各种各样的非线性效应。但对于大多数问题来说这样的假设是足够的,而且能得到相对简单的方程形式。
1. 应力张量与第一第二粘性系数
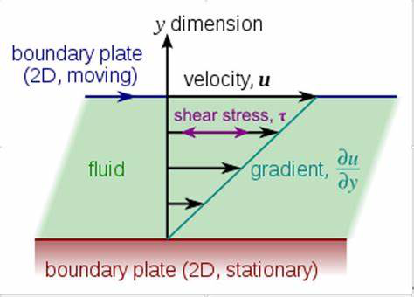
最简单的一种非粘性的各向同性流体,其应力张量的对角元都为 $-p$,这意味着每个面元上受到的力是垂直于面元的,单位面积上受到的力为流体在该处的压强,因此对角元 $-p$ 给出的就是压强 $p$。但实际情况中流体是有粘性的,例如下图
图 1:牛顿粘性实验
当 $y$ 方向相邻两侧流体的水平速度 $u$ 有梯度时,就会产生一个剪应力 $\tau=\mu \,\mathrm{d}{u} / \,\mathrm{d}{y} $,$\mu$ 被称为第一粘性系数。继续假设流体是各向同性的,那么似乎应该有 $T_{ij}=\mu \,\mathrm{d}{u} _j/ \,\mathrm{d}{x} _i$($i\neq j$)。但这样实际上是有问题的,在我们上面的牛顿黏性实验中,应力张量的非对角元实际上不止有 $T_{21}$,否则考察其中的一个微元,上面受到的向右的力比下面受到的向右的力更大,取足够小的微元,它的单位体积角动量将会趋于无穷大。这也意味着应力张量必须是对称张量。在上面的牛顿粘性实验中,事实上每一水平层流体,沿 $x$ 方向相邻两个紧挨着的流体微元,将会有 $y$ 方向的面力。也就是说 $T_{12}=T_{21}$。最终,我们可以把 $T_{ij}$ 改写为 $\mu ( \,\mathrm{d}{u} _j/ \,\mathrm{d}{x} _i+ \,\mathrm{d}{u} _i/ \,\mathrm{d}{x} _j)=2\mu S_{ij}$($i\neq j$)。
上面的讨论仍然存在问题。既然 $T_{ij}$ 对角元全相等(为 $-p$),那么对于各向同性的流体,应力张量矩阵 $T_{ij}$ 应当在正交相似变换下对角元应当仍是 $-p$。但从牛顿粘性实验的 $T_{ij}$ 出发很容易发现这是错误的。为了修正使得 $T_{ij}$ 各向同性,我们需要将第一粘性系数也考虑进 $T_{ij}$ 的对角元中:$T_{ij} = -p\delta_{ij}+2\mu S_{ij}$。
上面的讨论还没结束。对于可压缩流体,流体微元的密度改变,一般而言,静压强 $p$ 应当是密度 $\rho$ 的函数。但是,流体在压缩和膨胀的过程中,当 $S_{mm}=\nabla\cdot u\neq 0$,流体除了静压强 $p$ 以外,还可能会额外多出一个粘性压强。我们设第二粘性系数 $\mu_\nu$,并假设这个过程使得压强在 $p$ 基础上增大了 $\mu_\nu S_{mm}$(最终表现为 $T_{ij}$ 的对角元的平均值),那么可以写出最终的本构方程:
\begin{equation}
T_{ij}=-p\delta_{ij}+2\mu \left(S_{ij}-\frac{2}{3}S_{mm}\delta_{ij} \right) +\mu_\nu S_{mm} \delta_{ij}=-p\delta_{ij}+\tau_{ij}~.
\end{equation}
2. Navier-Stokes 方程(NS 方程)
整理上面的方程:
\begin{equation}
\begin{aligned}
\rho \frac{\mathrm{d}{u_j}}{\mathrm{d}{t}} &=\rho g_j+ \frac{\partial}{\partial{x_i}} T_{ij},\\
T_{ij}&=-p\delta{ij}+\tau_{ij}\\
&=-p\delta_{ij}+2\mu \left(S_{ij}-\frac{2}{3}S_{mm}\delta_{ij} \right) +\mu_\nu S_{mm} \delta_{ij}~.
\end{aligned}
\end{equation}
将应力张量表达式代入流体力学动量方程组,我们就得到了著名的
Navier-Stokes 方程:
\begin{equation}
\rho \frac{\mathrm{d}{u_j}}{\mathrm{d}{t}} =- \frac{\partial p}{\partial x_j} +\rho g_j+ \frac{\partial}{\partial{x_i}} \left[\mu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i} \right) + \left(\mu_\nu-\frac{2}{3}\mu \right) \frac{\partial u_m}{\partial x_m} \delta_{ij} \right] ~.
\end{equation}
当流体内部温度的差距较小时,
第一粘性系数和第二粘性系数可以近似认为是常数。那么上式可以简化表达为
\begin{equation}
\rho \frac{\mathrm{d}{u_j}}{\mathrm{d}{t}} =- \frac{\partial p}{\partial x_j} +\rho g_j+\mu \frac{\partial^{2}{u_j}}{\partial{x_i}^{2}} + \left(\mu_\nu+\frac{1}{3}\mu \right) \frac{\partial}{\partial{x_j}} \frac{\partial u_m}{\partial x_m} ~.
\end{equation}
所以,对于
不可压缩流体,$ \frac{\partial u_m}{\partial x_m} =0$,有方程
\begin{equation}
\rho \frac{\mathrm{d}{ \boldsymbol{\mathbf{u}} }}{\mathrm{d}{t}} =-\nabla p+\rho \boldsymbol{\mathbf{g}} +\mu \nabla^2 \boldsymbol{\mathbf{u}} ~.
\end{equation}
对于远离固体边界的流体,有时可以作近似处理,看成是无粘性的流体。此时的方程简化为
欧拉方程。
\begin{equation}
\rho \frac{\mathrm{d}{ \boldsymbol{\mathbf{u}} }}{\mathrm{d}{t}} =-\nabla p+\rho \boldsymbol{\mathbf{g}} ~.
\end{equation}