数值解线性方程组(高级)
贡献者: addis
1我们在前面两节已经讨论了线性方程组的最基本解法--高斯消元法,以及在实际编写算法时需要考虑到的数值问题--Pivoting。
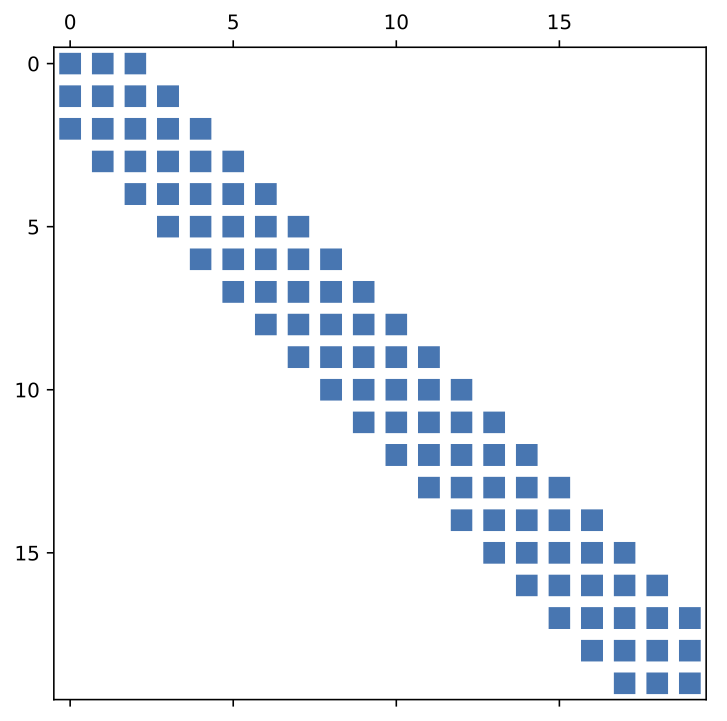
先来看一张图片
这一节我们就来探究一下这张图片的由来,以及它在解线性方程组中的重要意义。
事实上,这张图片是一个 $20\times20$ 的五对角矩阵(pentadiagonal matrix)。而产生这个矩阵的问题,则是求解一个跳板的弹性形变,也就是所谓的欧拉—伯努利梁方程。
1. 跳板模型
事实上,对于理解本节的内容,甚至整个专栏,同学们并不需要懂得任何固体力学的知识。在这里,我们不会讨论这个跳板模型是如何构造的,甚至这一节也不会讨论是如何从模型离散化成为这样一个五对角矩阵的。关于离散化的内容,涉及到了有限微分和有限元分析,我们会在后面详细讨论。这里我只给出生成这个矩阵的完整代码。
import numpy as np
import scipy
import scipy.sparse
import scipy.sparse.linalg
import matplotlib.pyplot as plt
def divingboardmatrix(n, L):
""" Generate matrix to diving board problem.
Parameters
----------
n : int, number of points
L : float, length of the board
Returns
-------
scipy.sparse : matrix for the problem
"""
# The stencil is [1, -4, 6, -4, 1]
A = scipy.sparse.diags([1, -4, 6, -4, 1], [-2, -1, 0, 1, 2], shape=(n, n))
A = A.tocsc()
A[0, 0] = 7
A[n-2, n-2] = 5
A[n-2, n-1] = -2
A[n-1, n-1] = 2
A[n-1, n-2] = -4
A[n-1, n-3] = 2
hinv = 1.0*n/L
A = A*(hinv**4)
return A
def loadvector(n, L, p, v, pos):
""" Generate rhs to diving board problem.
Parameters
----------
n : int, number of points
L : float, length of the board
p : int, number of people
v : float, average weight of one person
pos : float, position to put the load
Returns
-------
numpy.array : rhs for the problem
"""
x = np.linspace(0, L, n)
weight = 20
area = 0.2
material = 2.7e-4
f = -v*p*np.ones(n)
a = -weight*np.ones(n)
var = (x >= (pos-area)) & (x <= pos)
b = (a + var*f)*material
return b
这段代码中 divingboardmatrix(n,L) 会生成一个 $n\times n$ 的 $A$ 矩阵,而 loadvector(n, L, p, v, pos) 则会根据板的长度 $L$ ,上面站的人数 $p$ ,每个人的平均重量 $v$ 和这些人所站的位置 $\rm{pos}$ 来生成对应方程组的向量 $b$ 。通过求解 $Ax=b$ ,得到的 $x$ 向量,就是对应位置跳板的位移。
举个例子
我们假设板长为 4 米,板头的一端固定,另一端站上四个人,平均 75 公斤。
# Setup
nx = 1500
L = 4 # length of the board
p = 5 # number of people
v = 75 # average weight per person
pos = L # position of the load
# Construct matrix
A = divingboardmatrix(nx, L)
# right hand side
b = loadvector(nx, L, p, v, pos)
# solve
y = scipy.sparse.linalg.spsolve(A,b)
fig, ax = plt.subplots(1, figsize=(8, 6))
x = np.linspace(0, L, nx)
ax.plot(x, y, linewidth=8, color='C1')
# create waves
xwaves = np.linspace(0, L, 50)
waves = -1+0.05*np.random.rand(50);
ax.fill_between(xwaves, -2, waves)
# setups
ax.set_xlim([0, L])
ax.set_ylim([-2, 1])
ax.set_title('Diving board deflection')
回到正题
细心的同学可能已经注意到了,在求解线性方程组的时候我都用到了和前面两节不同的函数 scipy.sparse.linalg.spsolve。这也是我们这一节要讨论的重点,稀疏矩阵形式对求解线性方程组的影响。这种矩阵也是对微分方程离散化后最常见的结果之一。
所谓稀疏矩阵(sparse matrix)就是矩阵中大多数的元素都是 0 的矩阵。对于这类矩阵,通常情况下我们只需要存储那些非 0 的元素和他们所在的行和列的序号,而不必存储所有的 0 元素,这样不仅可以大大的节省存储空间,也会提高运算效率。
对比实验
我们来看一下,如果我们使用普通的线性方程求解,也就高斯消元法,和利用对角矩阵结构特性的部分消元法的运算时间对比。
注意:小伙伴们可能需要 ipython 或者 jupyter notebook 才能运行下面的计时程序。
这里我们的矩阵尺寸为 1500。
A_full = scipy.sparse.csc_matrix.todense(A)
%% timeit -r 5 -n 5 -o
y = scipy.linalg.solve(A_full,b)
采用高斯消元,运算时间为
581 ms ± 6.29 ms per loop (mean ± std. dev. of 5 runs, 5 loops each)
对比
%%timeit -r 5 -n 5 -o
y = scipy.sparse.linalg.spsolve(A,b)
针对对角矩阵的算法:
2.56 ms ± 265 µs per loop (mean ± std. dev. of 5 runs, 5 loops each)
可以明显看到两种算法的运算时间有着巨大的区别。有兴趣的小伙伴也可以按照我讲高斯消元那一节的方式,画出运算时间和矩阵尺寸的关系图。
原理解析
上面这个例子所用到的五对角矩阵,实际上也可以被理解为是一个稀疏矩阵。对于这样的五对角矩阵而言,如果进行基本的高斯消元或者 LU 分解,我们并不需要完整遍历每一行和每一列。事实上,每一步消元过程只需要对附近的两行两列进行运算,因此这个消元过程的运算复杂度并不是 $\mathcal{O}(n^3)$ ,而是 $\mathcal{O}(2^2n)$ 的。
同样的,对于三对角矩阵,还存在着一种专门针对它的托马斯算法
更普遍的结论是,对于带宽为 $k$ 的 $n\times n$ 对角矩阵,这里的带宽可以理解为所有非零元素与对角线的最远距离,(上面例子里的五对角矩阵中 $k=2$ ,而三对角矩阵的 $k=1$ )求解这样的线性方程组的运算复杂度为 $\mathcal{O}(k^2n)$ 。当这个 $k$ 不随问题尺寸 $n $ 变化时,这样的算法复杂度实际上是线性的。