南京理工大学 2008 量子真题
贡献者: 待更新
声明:“该内容来源于网络公开资料,不保证真实性,如有侵权请联系管理员”
1. 请考生在下列 12 题中选作 10 题,每题 15 分,满分 150 分。
- 1) 当势能 $V(x)$ 改变一个常量 $C$ 时, 即 $V(x) \rightarrow V(x) + C$, 粒子的波函数数中与时间无关部分变化否?粒子的能量本征值变化否?
2) 量子力学有哪些假定? - 利用测不准关系估计一维线性谐振子的基态能量。已知算符 $\hat{F}$ 的不确定度为 \[ \overline{(\Delta \hat{F})^2} = \overline{\hat{F}^2}- \overline{\hat{F}} ^2.~ \]
- 求下列算符对易关系式:
1) $\hat{L}_x, \hat{P}_x - \hat{P}_x \hat{L}_x=?$
2) $\hat{L}_y, \hat{P}_x - \hat{P}_x \hat{L}_y=?$
3) $\hat{L}_z, \hat{P}_x - \hat{P}_x \hat{L}_x=?$
- 证明:$L = \sqrt{6\hbar}, \, L_z = \pm \hbar$ 的氢原子中的电子,在 $\theta = 45^\circ$ 和 $135^\circ$ 的方向上被发现的概率最大。
- 带有电荷 $e$ 的一维线性谐振子,在 $t = 0$ 时处于基态,$t > 0$ 时处于方向沿 $x$ 轴正方向的弱电场 $\epsilon = \epsilon_0 e^{-t/\tau}$ 之中($\tau$ 为大于零的常数),试求该谐振子在长时间后处于第一激发态的概率。
- 证明:为了保证角动量算符的 $z$ 分量 $L_z = -i\hbar \frac{\partial}{\partial \varphi}$ 是厄密算符,波函数 $\psi(r, \theta, \varphi)$ 必须满足周期性边界条件 $\psi(r, \theta, \varphi) = \psi(r, \theta, \varphi + 2\pi)$。
- 在自旋态下 $\chi_{\frac{1}{2}}(s_z) = \begin{pmatrix} 1 \\ 0 \end{pmatrix}$,求 $\overline{\Delta s_x^2}$ 和 $\overline{\Delta s_y^2}$。
- 设在 $\hat H_0$ 表象中,$\hat{H} = \begin{pmatrix} E_1^{(0)} + a & b \\ b & E_2^{(0)} + a \end{pmatrix}$,$(a, b \text{为小量,实数})$,
1)用微扰论求能量本征值,准确到二级近似;2)严格求解能量本征值并与微扰论的计算结果比较。
- 设复原子处于基态,求电子处于经典力学不允许区 $(E - V = T < 0)$ 的概率。
- 试证明 $\psi(x) = \sqrt{\frac{\alpha}{3\sqrt{\pi}}} e^{-\frac{1}{2}\alpha^2 x^2} (2\alpha^3 x^3 - 3\alpha x)$ 是一维线性谐振子的波函数,并求此波函数对应的能量本征值。
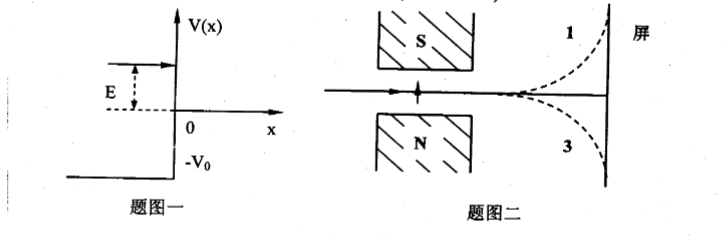
- 试求从左侧入射的粒子 ($E > 0$) 在下列势垒壁 $x = 0$ 处的反射系数。参见题图一。
- 设有一束极化电子(电子极化意指电子自旋有确定的取向),处于 $l = 0$ 的状态。在通过方向确定的不均匀磁场后分裂为强度不同的两束,其中自旋平行于磁场方向的一束与自旋平行于磁场方向的另一束之强度比为 1:3。求该入射的极化电子束自旋方向与外磁场方向的夹角大小(参见题图二)。
附:
氢原子的能量本征值为:
\[E_n = -\frac{\mu e^4}{2\hbar^2 n^2}, \, n=1,2,3,\ldots~\]
氢原子的基态波函数为:\[\psi_1 = \frac{1}{\sqrt{\pi a^3}} e^{-r/a}, \quad \text{玻尔半径: } a = \frac{\hbar^2}{\mu e^2}~\]
几个球谐函数:\[Y_{00} = \frac{1}{\sqrt{4\pi}}, \quad Y_{10} = \sqrt{\frac{3}{4\pi}} \cos \theta, \quad Y_{1\pm1} = \mp \sqrt{\frac{3}{8\pi}} \sin \theta e^{\pm i\varphi}~\]
\[Y_{20} = \sqrt{\frac{5}{16\pi}} (3\cos^2 \theta - 1), \quad Y_{2\pm1} = \mp \sqrt{\frac{15}{8\pi}} \sin \theta \cos \theta e^{\pm i\varphi}, \quad Y_{2\pm2} = \sqrt{\frac{15}{32\pi}} \sin^2 \theta e^{\pm i 2\varphi}~\]
一维线性谐振子的基态波函数:\[\varphi_0 = \sqrt{\frac{\alpha}{\sqrt{\pi}}} e^{-\frac{1}{2} \alpha^2 x^2}~\]
一维线性谐振子的第一激发态波函数:\[\varphi_1 = \sqrt{\frac{2\alpha}{\sqrt{\pi}}} \alpha x e^{-\frac{1}{2} \alpha^2 x^2}, \quad \alpha = \sqrt{\frac{\mu \omega}{\hbar}}~\]
定积分:\[\int_{0}^{\infty} x^{2n} e^{-\alpha x^2} dx = \frac{(2n-1)!!}{2^{n+1}} \sqrt{\frac{\pi}{\alpha^{2n+1}}}, \quad (2n-1)!! = 1 \cdot 3 \cdot 5 \cdot \cdots \cdot (2n-1)~\]