南京理工大学 2010 年研究生入学考试试题普通物理（B）

贡献者：待更新

　　声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 一。填空题(32 分，每空 2 分)

已知一电子的运动方程可表示为 $r = b \cos ω t \vec{i} + b \sin ω t \vec{j} + c t \vec{k}$ ，式中 $a, b$ 为常数， $t$ 以秒计。 $r$ 以来计，随在 $t$ 时刻，电子的速度为__________，加速度为 ___________。
一质量为 $m$ 的小球系在长为 $L$ 的细绳的一端，绳的另一端固定于 $O$ 点。先使小球以 $v_{0}$ 速度做圆周水平匀速运动，然后细绳逐渐缩短，绳始终与运动方向夹角为 $θ$ 的小球的速度表达式为___________，细绳的张力为多大为 ___________。
设一平面简谐波沿 $x$ 轴正方向传播，已知 $x = 0$ 处原点的振动方程为 $y = A \cos (ω t - π / 3)$ ,波速为 $v$ 。波在 $x = L$ 处终止反射，则 $x = x_{0}$ 处 $(x_{0} < L)$ 原点由于反射被引起的振动方程为 ___________， $x_{0}$ 处是波节位置的条件是 $x_{0} =$ ___________。
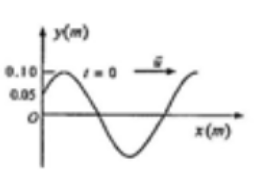
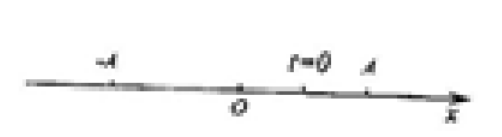
如图所示，一沿正 $x$ 方向传播的平面简谐波，波速为 $v = 200 m / s$ ，波长 $λ = 20 m$ ，则 $x = 0$ 处质点的振动方程为_________，该平面简谐波方程为_________。

图 1
$2 m o l$ 氧气在 27°C 时的内能等于 ___________，其分子的平均动能是 ___________，平均平动动能是 ___________。
设一个气体分子的密度分布函数为 $f (v)$ ，则单位体积中， $v_{1} \to v_{2}$ 区间内的分子数为 ___________。
带电量为 $q$ 半径为 $R_{1}$ 的导体球 $A$ ，与内、外半径分别为 $R_{2}$ 和 $R_{3}$ 接地的同心金属球壳 $B$ 间充满介电常数为 $ε$ 的介质，构成一球形电容器。则该电容器的电容 $C =$ ___________。设导体球 $A$ 带电 $q$ ，则该电容器内任一点 $P$ 处的电场强度 $E =$ ___________，电容器储存的电能___________。若球壳 $B$ 接地，则导体球 $A$ 的电势为 ___________。

2. 二、填空题(32 分。每空 2 分)

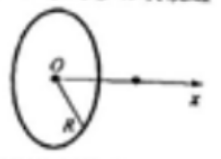
　　 1. 半径为 $R$ 的圆环，均匀带电，单位长度的电量为 $λ$ 。以每秒 $n$ 转绕通过环心并与环面需直的轴作等速转动。则环的等效磁矩大小为___________，轴线上距坏心为 $x$ 处的任一点 $p$ 的磁感应强度大小为___________。

图 2

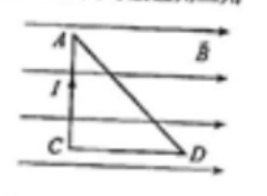
　　 2. 均匀磁场 $B$ 中置一直角边长为 $a$ 通有强度为 $I$ 的稳恒电流的等腰直角三角形线圈 $A C D$ 。使线圈绕 $A C$ 边匀速转动，线圈平面与磁场方向平行。如图所示，现线圈所受的力矩的大小为___________。在磁力矩作用下，线圈平面绕 $A C$ 边转过 $π / 3$ 圈，磁力矩做的功（ $I$ 在旋转过程中不变）为___________。

图 3

　　 3. 在恒真空场的均匀磁场中，长为 $l$ 的导体棒 $a b$ 以 $ω$ 逻时针绕 $a$ 点勾速转动，如图，则切出电动势的大小为___________，且 ___________ 点的电势为。

图 4

　　 4. 在真空中，一平面电磁波的磁场 $B = B_{0} = B_{0} \cos (ω (t + \frac{z}{c})), (T)$ 。则该电磁波的传播方向为___________，电场强度为___________。

　　 5.用氮-氖撒光器发出的波长为 $632.8 n m$ 的单色光徽牛领环实验，已知所用平凸透镜的鱼率半径为 $10.0 m$ ，平面直径为 $3.0 c m$ ，则能观察列___________，条暗坏。若把整个装置放入水中 $(η = 1.33)$ ，总观察到___________，条暗坏:

　　 6、两个偷报化方向相互看宜的偏报片平行放置，组合战正交偏报片。现让光强为 $I_{0}$ 的一東自然光垂直射入谈正交偏探片，则透射光强为___________。若在阿偏振片之间放入第三块偷报片。其偏化方向与第一块偷振片的偏振化方向央角为 30”，则透射光强为___________。

　　 7、动能 $E = 1.53 M V$ 的电子运动的德布罗意波长为___________。

　　 8、处于第一灏发态的氢原子的势能为___________，其核外电子绕核运动的动能为___________。

　　 9. 已知一维无限深势井中粒子的波函数为: $ψ_{n} (x) = \sqrt{\frac{2}{a}} \sin \frac{n π}{a} x$ . 设 $n = 1$ 时, 粒子在 $x = \frac{a}{3}$ 处出现的概率密度为: ___________。

3. 三、(12 分)

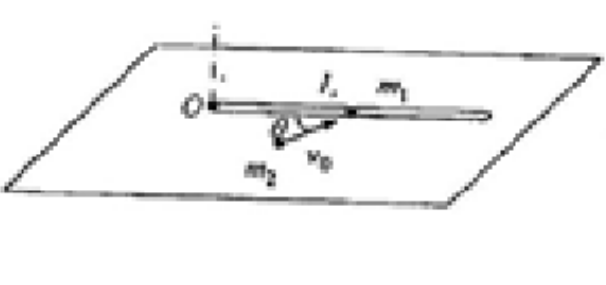
　　如图所示，水平桌面上。一长为 $l = 1.0 m$ :质量为 $m_{1} = 3.0 k g$ 的匀质烟杆，一端围定于 $O$ 点，细杆可经过 $O$ 点竖直轴在水平桌面上标动烟杆与桌面间的摩操系数为 $μ = 0.20$ ，开始时杆静止。现有一质量为 $m_{2} = 20 g$ 速度 $v_{0} = 400 m / s$ ，沿水平方向以与杆成 $θ = 30^{\circ}$ 常射入杆的中点日留在杆内。来: (1)擅击后杆开始神动的角速度大小: (2)子弹射入后,细扦所受摩擦力矩: (3)烟杆的角加速度

图 5

4. 四、(12 分)

　　如图，一质量 $m = 2.0 k g$ 的物体沿 $x$ 轴做简谐振动，振幅为 $0.12 m$ ，周期为 $2 t$ 初始时 $x_{0} = 0.06 m$ 并向 $x$ 独正向运动。求: (1)物体的运动方程: (2)物体从初始时刻运动到平衡位置所需要最短时间; (3)物体在平衡位置时所具有的机械能:

图 6

5. 五. (18 分)

　　一摩尔的双原子理想气体，初始时压强为 $2 a_{0}$ ，体积为 $20 V_{0}$ 。先等压膨胀至体积变为 2 倍，再等容冷却至原来温度，最后等温压缩回到初态。

作出该过程中 $p - V$ 图；
求气体在各过程中的功；
该循环的效率。

6. 六、(12 分)

　　一无限长均匀带电圆柱，体电荷密度为 $ρ$ ，截面半径为 $R$ 。

用高斯定理求出柱体内外电场强度分布；
求出柱体内外的电势分布（以柱面为电势零点）。

7. 七、(10 分)

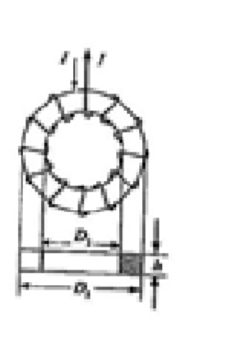
　　如图为矩形，总匝数为 $N$ 的通有电流 $I$ 螺绕环，尺寸如图所示。求：

　　 (1) 环内磁感应强度的分布；

　　 (2) 通过螺绕环截面（图中阴影区）的磁通量。

图 7

8. 八、(10 分)

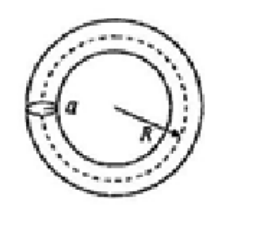
　　一螺绕环，横截面的半径为 $a$ ，中心线的半径为 $R$ ， $R ≫ a$ 。其上由表面绝缘的导线均匀地绕密绕两个线圈，一个 $N_{1}$ 匝，另一个 $N_{2}$ 匝。求：

两线圈的自感 $L_{1}$ 和 $L_{2}$ ；
两线圈的互感 $M$ ；

图 8

9. 九、(10 分)

　　光栅每厘米有 $2500$ 条纹线，且刻痕宽度 $b$ 是缝宽 $a$ 的 3 倍。若以 $λ_{1} = 600 n m$ 的单色光垂直入射到光源上，求：

光栅常数；
在单缝衍射的中央明纹区域内，最多可见到多少条主极大明纹；
若用另一波长为 $λ_{2}$ 的单色光垂直入射，发现其第 3 级与 $λ_{1}$ 的第 2 级主极大明纹重合， $λ_{2}$ 的量值为多少？

10. 十、(10 分)

　　 $π$ 介子，相对静止时测得其平均寿命 $τ_{0} = 1.8 \times 10^{- 8} s$ ，若使其以 $v = 0.6 c$ 的速度离开加速器，求：

　　 (1) 从实验室观测， $π$ 介子的平均寿命；

　　 (2) 若在寿命为 $τ_{0}$ 的介子上测量，能测到的实验室后退的距离。

　　附常用物理常数:

电子静止质量 $m_{0} = 9.1 \times 10^{- 31} (k g)$
普朗克常数 $h = 6.63 \times 10^{- 34} (J \cdot s)$
普适气体常数 $R = 8.31 (J / m o l \cdot K)$
引力常量 $G = 6.67 \times 10^{- 11} N \cdot m^{2} / {kg}^{2}$
电子电量 $e = 1.6 \times 10^{- 19} (C)$
真空中光速 $c = 3 \times 10^{8} (m / s)$
玻尔兹曼常量 $k = 1.38 \times 10^{- 23} (J / K)$
真空电容率 $ε_{0} = 8.85 \times 10^{- 12} C^{- 2} N^{- 1} m^{- 2}$

南京理工大学 2010 年 研究生入学考试试题 普通物理（B）