μ子

贡献者：待更新

　　（本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

1. $\mu$ 子

　　 $\mu$ 子（/ˈmjuːɒn/；来自用于表示它的希腊字母 mu（$\mu$）)是一种类似于电子的基本粒子，电荷量为−1e，自旋为 1/2，但是 $\mu$ 子拥有比电子更大的质量。$\mu$ 子被归类为轻子。与其他轻子一样，子不被认为有任何亚结构——也就是说，它不被认为由任何更简单的粒子组成。

　　 $\mu$ 子是一种不稳定的亚原子粒子，其平均寿命为 2.2 $\mu$s，这比许多其他亚原子粒子都要更长。如同非基本粒子的中子的衰变一样（中子寿命约为 15 分钟），$\mu$ 子的衰变（按亚原子标准）发生得很慢，这是因为 $\mu$ 子的衰变是完全由弱相互作用引起的（而不是更强大的强相互作用者电磁相互作用）；且因为 $\mu$ 子和它的衰变产物间的质量差很小，所以它的衰变只有很少的动力学自由度。$\mu$ 子的衰变几乎总是产生至少三个粒子，其中必须定括一个与 $\mu$ 子拥有相同电荷的电子以及两个不同类型的中微子。

　　像所有基本粒子一样，$\mu$ 子也有相应的反粒子，后者拥有与前者相反的电荷（+1e），但两者的质量和自旋则是相同的，这个反粒子就是反 $\mu$ 子（也称为正 $\mu$ 子）。$\mu$ 子被表示为 $\mu$−，反 $\mu$ 子则是 $\mu$+。$\mu$ 子以前被称为 $\mu$ 介子，但现代粒子物理学家不再将其归类为介子，因此物理界也就不再使用 $\mu$ 介子这个名称了。

　　 $\mu$ 子的质量为 105.66 MeV/c2，这大约是电子的 207 倍。由于 $\mu$ 子的质量更大，当 $\mu$ 子遇到电磁场时，其加速不会那么快，也不会发射那么多轫致辐射（减速辐射）。这使得拥有给定能量的 $\mu$ 子在物质中可以比电子穿透得更深，因为电子和 $\mu$ 子的减速主要是由于轫致辐射机制所导致的能量损失。例如，由宇宙射线撞击大气层所产生的所谓 “次级 $\mu$ 子” 可以穿透到地表，甚至深入矿井。

　　因为 $\mu$ 子的质量和能量比起放射性过程的衰变能量来说非常大，所以 $\mu$ 子从来都不会由放射性衰变产生。然而，它们可以大量地产生于正常物质中的高能相互作用、涉及到强子的某些粒子加速器实验或者宇宙线与物质间自然发生的相互作用中。这些相互作用通常先产生 $\pi$ 介子，$\pi$ 介子通常会衰变成 $\mu$ 子。

　　与其他带电轻子一样，$\mu$ 子有一种相对应的 $\mu$ 子中微子，后者被表示为 $v_\mu$。$\mu$ 子中微子不同于电子中微子，它们不参与相同的核反应介子，$\pi$ 介子通常会衰变成 $\mu$ 子。

　　与其他带电轻子一样，$\mu$ 子有一种相对应的 $\mu$ 子中微子，后者被表示为 $v_\mu$。$\mu$ 子中微子不同于电子中微子，它们不参与相同的核反应

2. 历史

　　 $\mu$ 子是由卡尔·安德森和 Seth Neddermeyer 于 1936 年在加利福尼亚理工学院研究宇宙辐射时发现的。安德森注意到一些粒子穿过磁场时所产生的弯曲路径与电子和其他已知粒子都不相同。它们带负电，在速度相同的情况下，它们在磁场中的路径的弯曲程度不如电子，同时又比质子要更加弯曲。$\mu$ 子所带的负电荷量被默认与电子相同，因次它们路径曲率的差异就意味着 $\mu$ 子的质量大于电子但小于质子。安德森最初称这种新粒子为 mesotron，采用了希腊词前缀 meso-，意思就是 “中间”。$\mu$ 子的存在于 1937 年被 J. C. Street 和 E. C. Stevenson 的威尔逊云雾室实验所证实。[1]

　　理论物理学家汤川秀树在发现介子之前就已经预测了质量在介子范围内的粒子：[2]

　　用以下方式修改海森堡和费米理论似乎很自然。重粒子从中子态状态到质子状态的转变并不总是伴随着轻粒子的发射。这种转变有时会被另一个重粒子占据。

　　由于其质量，$\mu$ 子最初被认为是汤川秀树所预测的粒子，但后来被证明拥有错误的性质。汤川预测的粒子（即 $\pi$ 介子）最终在 1947 年被确定（再次来自宇宙射线相互作用），并被证明不同于早期发现的 $\mu$ 子，$\pi$ 介子具有介导核力的正确性质。

　　已知两种具有中间质量的粒子以后，更一般的术语 “介子” 被用来指代那些质量位于电子和核子之间的粒子。此外，为了在发现第二种介子后区分两种不同类型的介子，先被发现的那种介子被重命名为 $\mu$ 介子（希腊字母 $\mu$（mu），对应于 m），1947 年才被发现的那种介子（汤川粒子）则被命名为 $\pi$ 介子。

　　随着后来更多类型的介子在加速器实验中被发现，物理学家最终发现 $\mu$ 介子不仅与（质量大约相同的）$\pi$ 介子之间存在显著差异，而且与所有其他类型的介子也非常不同。部分区别在于 $\mu$ 介子不像 $\pi$ 介子那样参与核力相互作用（这是汤川理论所要求的）。新发现的介子在核相互作用中表现得像 $\pi$ 介子，但不像 $\mu$ 介子。此外，$\mu$ 介子的衰变产物包括一个中微子和一个反中微子，而不是像在其他带电介子的衰变中观察到的那样只有一个中微子或一个反中微子。

　　在成形于 1970 年代的粒子物理学标准模型中，除了 $\mu$ 介子之外的所有其他介子都被理解为强子。也就是说，这些粒子都是由夸克组成的，因此都受制于核力。在夸克模型中，介子不再由质量来定义（因为已经发现存在质量非常大的介子，这些介子的质量比核子还要大），介子被认为是由正好两个夸克（夸克和反夸克）组成的粒子，这一点与重子不同，后者是由三个夸克组成的（质子和中子是最轻的重子）。然而，$\mu$ 介子已经被证明是像电子一样的基本粒子（轻子），而且没有夸克结构。因此，对于基于粒子结构夸克模型的 “介子” 这个术语的新意义和新用法来说，$\mu$ 介子根本不是介子。

　　随着定义的改变，$\mu$ 介子这个术语已经被抛弃了，现在物理学家都尽可能用现代术语 $\mu$ 子来代替 $\mu$ 介子，$\mu$ 介子这个名称仅剩下了历史意义。在新的夸克模型中，其他类型的介子有时会被继续用较短的术语来表示（例如，$\pi$ 介子简称为 pion），但 $\mu$ 子保留了较短的名称 muon，旧术语 “$\mu$ 介子” 再也没有被提及了。

　　最终承认 “$\mu$ 介子”$\mu$ 子是一个简单的 “重电子” 并且在核相互作用中没有任何作用在当时似乎是如此的不协调和令人惊讶，以至于诺贝尔奖获得者拉比有这么一句名言：“谁点的？”[3]

　　在 1941 年的罗西-霍尔实验中，$\mu$ 子首次被用来观察狭义相对论所预测的时间膨胀（或者长度收缩）。

3. μ子源

　　到达地表的 $\mu$ 子是宇宙射线与地球大气层粒子碰撞的衰变产物。[4]

　　在地球表面每分钟每平方厘米大约有 10,000 个 $\mu$ 子到达。这些带电粒子是宇宙射线撞击大气层上层中的分子的副产物。以相对论性速度运动的 $\mu$ 子在被其他原子吸收或偏移而衰减之前能够穿透几十米厚的岩石和其他物质。[5]

　　当宇宙射线质子撞击高层大气中的原子核时会产生π介子。这些π介子在相对较短的距离（若干米）内便衰变为 $\mu$ 子（它们所偏好的衰变产物）和 $\mu$ 子中微子。来自这些高能宇宙射线的 $\mu$ 子通常以接近光速的速度沿着与初始质子大约相同的方向继续前进。虽然在没有相对论效应的情况下这些 $\mu$ 子的寿命所允许的半存活距离最多只有 456 米（$2.197\mu s * \ln\left(2\right) * 0.9997 * c$），但狭义相对论的时间膨胀效应（从地球参照系的观点）允许宇宙射线次级 $\mu$ 子在飞往地表的飞行中存活，因为在地球参照系中 $\mu$ 子由于其速度而具有更长的半衰期。从 $\mu$ 子的角度来看（惯性坐标系），则是狭义相对论的长度收缩效应使得这种穿透能够实现，因为在 $\mu$ 子的生命周期不受影响，但长度收缩导致通过大气层和地球的距离远短于地球静止参考系中所测量到的距离。这两种效应都是解释快速 $\mu$ 子不寻常的长距离存在的有效方法。

　　由于 $\mu$ 子能够不同寻常地穿透普通物质，像中微子一样，它们也可以在地下深处（地下 700 米处的 Soudan 2 探测器）和水下检测到，它们形成自然背景电离辐射的一个主要部分。如前所述，像宇宙射线一样，这种次级 $\mu$ 子辐射也是定向的。

　　粒子物理学家使用与上述相同的核反应（即强子-强子碰撞产生π介子束，然后π介子束在短距离内快速衰变为 $\mu$ 子束）来产生 $\mu$ 子束，例如用于 $\mu$ 子 g-2 实验的 $\mu$ 子束。[6]

4. μ子衰变

　　 $\mu$ 子是不稳定的基本粒子，比电子和中微子重，但比所有其他物质粒子轻。它们通过弱相互作用发生衰变。因为轻子族数在没有极不可能立即出现的中微子振荡的情况下是守恒的，$\mu$ 子衰变的产物之一必须是 $\mu$ 子型中微子，另一个必须是电子型反中微子（反 $\mu$ 子衰变则产生相应的反粒子，如下所述）。因为电荷必须守恒，$\mu$ 子衰变的产物之一总是与 $\mu$ 子具有相同电荷的电子（如果是正 $\mu$ 子，产物则是正电子）。因此，所有 $\mu$ 子至少衰变为一个电子和两个中微子。有时，除了这些必要的产物之外，还会产生其他没有净电荷和自旋为零的粒子（例如，一对光子或电子-正电子对）。

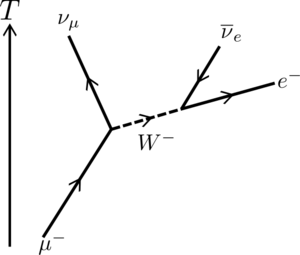
　　主导的 $\mu$ 子衰变模式（有时被以路易斯·米歇尔之名命名为米歇尔衰变）是最简单的可能：$\mu$ 子衰变为电子、电子型反中微子和 $\mu$ 子中微子。反 $\mu$ 子以镜像方式最常衰变成相应的反粒子：正电子、电子中微子和 $\mu$ 子型反中微子。用公式化的术语来说，这两种衰变就是:

\begin{equation} \mu^- \to e^-+v_e+v_\mu~ \end{equation}

\begin{equation} \mu^+ \to e^+ +v_e+v_\mu~ \end{equation}

正负 $\mu$ 子的平均寿命（τ=ħ/Γ）是(2.1969811±0.0000022) $\mu$s。[7]$\mu$ 子和反 $\mu$ 子寿命的相等已经被确定到优于 1/104 的精度。

图 1：$\mu$ 子最常见的衰变

3.1 被禁止的衰变

　　某些无中微子的衰变模式在运动学上是允许的，但出于所有实际目的，在标准模型中是被禁止的，甚至在中微子具有质量和存在振荡的情况下也是如此。轻子味守恒所禁止的例子有:

\begin{equation} \mu^- \to e^- + Y~ \end{equation}

和

\begin{equation} \mu^- \to e^- +e^+ + e^-~ \end{equation}

准确地说，在包含有质量中微子的标准模型中，类似于 $\mu^- \to e^- + Y$ 的衰变在技术上是可能的，例如通过中微子振荡将虚的 $\mu$ 子中微子转化为电子中微子，但是这种衰变在天文学上是不太可能的，因此在实验上是不可观测的：不到 1/1050 的 $\mu$ 子衰变会产生这样的结果。

　　对这些衰变模式的观察将构成超越标准模型理论的明确证据。这些衰变模式的分支分数的上限在许多实验中被测量，这些实验开始于 50 多年前。当前的 $\mu^+ \to e^+ + Y$ 分支分数上限在 2009-2013 年的 MEG 实验中被测量，结果为 4.2 × 1013。[8]

3.2 理论衰变率

　　来自费米黄金定则的 $\mu$ 子衰变宽度拥有能量量纲，而且必定与振幅的平方成正比，从而与费米耦合常数（ $G_F$）的平方成正比（费米耦合常数的平方的量纲为能量的负四次方）。通过量纲分析，这导致了萨金特法则的 $m_\mu$ 五次方依赖性，

\begin{equation} \Gamma=\frac{G^2_F m^5_\mu}{192\pi^3}\text{~}I\left({\frac{m_{\text {e}}^{2}}{m_{\ mu}^{2}}}\right)~ \end{equation}

在其中 $I(x)=1-8x-12x^2\ln x+8x^3-x^4,x=2E_e/ m_\mu c^2$ 则是传递给电子的最大能量的分数。

　　 $\mu$ 子衰变中电子的衰变分布已经用所谓的米歇尔参数参数化了。这四个参数的值在粒子物理学标准模型中被清楚地预测了，所以 $\mu$ 子衰变代表了对弱相互作用的时空结构的一个很好的检验。尚未发现与标准模型预测的偏差。对于 $\mu$ 子的衰变，米歇尔参数的标准模型值的预期衰变分布为

\begin{equation} \frac{d\Gamma}{d \cos \theta}\text{~} x^2[(3-2x)+P_\mu \cos \theta(1-2x)]~ \end{equation}

其中 $\theta$ 是 $\mu$ 子极化矢量 $P_mu$ 和衰变电子动量矢量之间的角度，$P_\mu= \left\lvert P_\mu \right\rvert $ 是向前极化的 $\mu$ 子的比例。将这个表达式对电子能量求积分可以得到子电子的角分布:

\begin{equation} \frac{d\Gamma}{d\cos \theta} \text{~} 1-\frac{1}{3}P_\mu \cos \theta~ \end{equation}

在极角上积分的电子能量分布（对于 $x<1$）是

\begin{equation} \frac{d\Gamma}{dx} \text{~}(3x^2-zx^3)~ \end{equation}

由于 $\mu$ 子在弱相互作用下衰变，因此宇称守恒被违反。将米歇尔参数的预期衰减值中的 $\cos \theta$ 替换为 $\cos \omega t$，其中的 $\omega$ 是 $\mu$ 子在均匀磁场中的拉莫进动的拉莫频率，它由下式给出:

\begin{equation} \omega=\frac{egB}{2m}~ \end{equation}

在其中 m 是 $\mu$ 子的质量，e 是电荷，g 是 $\mu$ 子 g 因子，B 是施加的场。

　　从使用标准的非进动的米歇尔参数计算的电子分布的变化可以看出其显示了弧度为 $\pi$ 的周期性。可以看出，这在物理上对应于大小为 $\pi$ 的相变，当角动量通过荷共轭算子的作用而改变时被引入了电子分布中，它在弱相互作用中是守恒的。

　　对 $\pi$ 子衰变中的宇称破缺的观察可以与弱相互作用中宇称破缺的概念（通常作为吴氏实验的扩展）以及由 $\pi$ 相变引入的角动量的变化相比较，π相变对应于在这种相互作用中具有不变性的荷宇称算子。这一事实适用于标准模型中的所有轻子相互作用。

5. μ子原子

4.1 负μ子原子

　　然而，负 $\mu$ 子可以通过替换普通原子中的电子形成 $\mu$ 子原子（以前称为 $\mu$-mesic 原子）。$\mu$ 子氢原子比典型的氢原子小得多，因为 $\mu$ 子那比电子大得多的质量使得其基态波函数的局域化程度比电子也高得多。在多电子原子中，当只有一个电子被 $\mu$ 子取代时，原子的大小继续由其他电子所决定，因此几乎不变。然而，在这种情况下，$\mu$ 子的轨道仍然比电子的原子轨道轨道更小，离原子核更近。

　　 $\mu$ 子氦是通过用 $\mu$ 子代替氦-4 中的一个电子而产生的。$\mu$ 子轨道离原子核更近，因此 $\mu$ 子氦可以被看作是氦的同位素，其原子核由两个中子、两个质子和一个 $\mu$ 子组成，外面只有一个电子。通俗地说，它可以被称为 “氦 4.1”，因为 $\mu$ 子的质量略大于 0.1amu。化学上，$\mu$ 子氦具有一个不成对的价电子，可以与其他原子成键，其行为更像氢原子，而不是惰性的氦原子。[9][10][11]

　　带有一个负 $\mu$ 子的重氢原子可能在 $\mu$ 子催化聚变的过程中发生核聚变，接着 $\mu$ 子可能离开新原子并诱导另一个氢分子发生聚变。这个过程会一直持续到负 $\mu$ 子被氦核俘获，并且在它发生衰变之前无法逃逸。

　　最后，束缚在常规原子上的负 $\mu$ 子的一种可能命运是被原子核中的质子通过弱相互作用捕获，这种过程类似于电子捕获。当这种情况发生时，质子会变成中子，并发射出 $\mu$ 子中微子。

4.2 正μ子原子

　　当一个 $\mu$ 子停在普通物质中时，它不能被质子俘获，因为它需要的是一个反质子。正 $\mu$ 子也不会被原子核吸引。相反，它与一个随机电子结合，并与这个电子共同形成一个被称为 $\mu$ 子偶素（Mu）的奇特原子。在这个原子中，$\mu$ 子充当了原子核。在这种情况下，正 $\mu$ 子可以被认为是氢的一种伪同位素，质量为质子的九分之一。因为 $\mu$ 子偶素的约化质量以及它的玻尔半径都非常接近于氢，这种短命的 “原子”（或 $\mu$ 子和电子的组合）的化学行为在一阶近似上跟氢的同位素（氕、氘和氚）很像。

　　正 $\mu$ 子和负 $\mu$ 子都可以是短命的π-$\mu$ 原子的一部分，π-$\mu$ 原子由 $\mu$ 子和带相反电荷的π介子组成。这些原子是 20 世纪 70 年代在布鲁克黑文和费米实验室的实验中被观察到的。[12]

6. 用于测量质子电荷半径

　　有望提供最精确的对质子的电荷半径均方根的确定的实验技术是对 $\mu$ 子氢中的原子跃迁所发射或吸收的光子的频率的测量。这种氢原子由质子和束缚于其上的带负电荷的 $\mu$ 子组成。$\mu$ 子特别适合这一目的，因为它的质量比电子大得多，这导致束缚态更紧密，因此与氢原子中的电子相比在 $\mu$ 子氢中的质子内发现它的可能性更大。[13]$\mu$ 子氢中的兰姆位移是通过使用激光将 $\mu$ 子从 2s 态驱动到激发的 p 态来测量的。2014 年对诱导两次这种（略有不同的）跃迁所需的光子的频率的测量结果分别为 50 THz 和 55 THz，根据现有的量子电动力学理论，这个测量结果给了我们质子的电荷半径适当的平均值，这个值为 0.84087±0.00039 fm。[14]

　　质子电荷半径的国际公认值是基于适当的测量结果平均值，这些结果是较旧的测量的结果，测量的是质子的不为零尺寸在原子对电子的散射以及来自激发的原子氢的光谱（光子能量）中所导致的效应。2014 年更新的官方值为 0.8751±0.0061 fm（与其他尺寸的比较可参见数量级）。[15]这一结果的预期精度比来自 $\mu$ 子氢的结果低大约 15 倍，然而它们的不确定度相差大约 5.6 倍（这种差异在科学计数法中被称为 5.6σ）。一次关于这一主题的世界专家会议决定排除 $\mu$ 子结果对 2014 年官方数值的影响，以避免隐藏这种神秘的差异。[16]这个 “质子半径之谜” 截至 2015 年底仍未解决，并引起了许多关注，部分原因是这两个测量结果都可能有效，这暗示着一些 “新物理” 的影响。[17]

7. 反常磁矩

　　反常磁矩是磁偶极矩的实验观测值和狄拉克方程理论预测值之间的差异。该值的测量和预测在量子电动力学的精度测试中非常重要。布鲁克黑文国家实验室（BNL）的 E821 实验[18]研究了 $\mu$ 子和反 $\mu$ 子在恒定外部磁场中的进动，这些粒子在一个封闭的存储环中循环。E821 于 2006 年报告了以下的平均值[19]

\begin{equation} a=\frac{g-2}{2}=0.00116592080(54)(33)~ \end{equation}

其中第一个误差是统计误差，第二个是系统误差。 $\mu$ 子反常磁矩的预测包括三个部分：

\begin{equation} \alpha_\mu^{SM}=\alpha_\mu^{QED}+\alpha^{EW}_\mu+\alpha_\mu^{had}~ \end{equation}

$\mu$ 子和电子的 g-因子之间的区别是由于它们的质量不同。由于 $\mu$ 子质量较大，来自标准模型弱相互作用的对反常磁矩的理论计算的贡献和来自涉及强子的贡献在当前的精度水平上是重要的，而这些效应对电子并不重要。$\mu$ 子的反常磁矩对超越标准模型的新物理学的贡献也很敏感，例如超对称性。因此，$\mu$ 子的反常磁矩通常被用作对标准模型之外的新物理的探针，而不是对量子电动力学的测试。[20] 在费米实验室进行的 $\mu$ 子 g-2 实验使用 E821 磁铁，该实验将提高这一测量的精度。[21]

8. μ子射线照相术和断层摄影术

　　因为 $\mu$ 子比 x 射线或γ射线更具穿透力，所以 $\mu$ 子成像可以被用于更厚的材料，或者更大的物体（如果是来源于宇宙射线的 $\mu$ 子）。一个例子是商业 $\mu$ 子断层摄影，用于对整个货物集装箱成像，以检测被屏蔽的核材料以及爆炸物或其他走私货物。[22]

　　基于宇宙射线源的 $\mu$ 子透射射线照相技术在 20 世纪 50 年代首次被用于测量澳大利亚隧道的覆盖层深度[23]，20 世纪 60 年代被用于寻找吉萨的卡夫拉金字塔中可能隐藏的密室。[24]2017 年，通过观测宇宙射线 $\mu$ 子，科学家发现了胡夫金字塔中的一个大空洞（长度最小为 30 m）。[25]

　　 2003 年，洛斯阿拉莫斯国家实验室的科学家开发了一种新的成像技术：$\mu$ 子散射层析成像。使用 $\mu$ 子散射层析成像，每个粒子的入射和出射轨迹都被重建，例如使用密封的铝漂移管[26]。自从这项技术被开发以来，几家公司已经开始使用它了。

　　 2014 年 8 月，决策科学国际公司宣布，它已获得东芝的合同，使用其 $\mu$ 子跟踪探测器来回收福岛核设施。[27]福岛第一核电站跟踪器（FDT）被提议进行几个月的 $\mu$ 子测量，以显示反应堆堆芯的分布。

　　 2014 年 12 月，东京电力报告称，他们将在福岛使用两种不同的 $\mu$ 子成像技术，一号机组使用 “$\mu$ 子扫描方法”（受损最严重，燃料可能已经离开反应堆容器），二号机组使用 “$\mu$ 子散射方法”。[28]

　　日本的反应堆退役国际研究所 IRID 和高能加速器研究机构将他们为一号机组开发的方法称为$\mu$ 子渗透法；1200 根用于波长转换的光纤在 $\mu$ 子与它们接触时会发光。[29]经过一个月的数据收集，人们希望能揭示出仍在反应堆内的燃料残余的位置和数量。这个测量始于 2015 年 2 月。[30]

　　 参考文献

　　 [1]Street, J.; Stevenson, E. (1937). "New Evidence for the Existence of a Particle of Mass Intermediate Between the Proton and Electron". Physical Review. 52 (9): 1003. Bibcode:1937PhRv...52.1003S. doi:10.1103/PhysRev.52.1003..

　　 [2]Yukawa, Hideki (1935). "On the Interaction of Elementary Particles" (PDF). Proceedings of the Physico-Mathematical Society of Japan. 17 (48): 139–148..

　　 [3]《科学与技术》；技术；谁点了μ子？”，作者:Marcia Bartusiak《纽约时报》；1987 年 9 月 27 日出版；检索于 2016 年 8 月 30 日.

　　 [4]Demtröder, Wolfgang (2006). Experimentalphysik 1 (4 ed.). Springer. p. 101. ISBN 978-3-540-26034-9..

　　 [5]Mark Wolverton (September 2007). "Muons for Peace: New Way to Spot Hidden Nukes Gets Ready to Debut". Scientific American. 297 (3): 26–28. Bibcode:2007SciAm.297c..26W. doi:10.1038/scientificamerican0907-26..

　　 [6]"Physicists Announce Latest Muon g-2 Measurement" (Press release). Brookhaven National Laboratory. 30 July 2002. Retrieved 2009-11-14..

　　 [7]J. Beringer et al. (Particle Data Group) (2012). "PDGLive Particle Summary 'Leptons (e, mu, tau, ... neutrinos ...)'" (PDF). Particle Data Group. Retrieved 2013-01-12..

　　 [8]Baldini, A.M.; et al. (MEG collaboration) (May 2016). "Search for the Lepton Flavour Violating Decay μμ+ → e+γ with the Full Dataset of the MEG Experiment". arXiv:1605.05081 [hep-ex]..

　　 [9]Fleming, D. G.; Arseneau, D. J.; Sukhorukov, O.; Brewer, J. H.; Mielke, S. L.; Schatz, G. C.; Garrett, B. C.; Peterson, K. A.; Truhlar, D. G. (28 Jan 2011). "Kinetic Isotope Effects for the Reactions of Muonic Helium and Muonium with H2". Science. 331 (6016): 448–450. Bibcode:2011Sci...331..448F. doi:10.1126/science.1199421. PMID 21273484..

　　 [10]Moncada, F.; Cruz, D.; Reyes, A (2012). "Muonic alchemy: Transmuting elements with the inclusion of negative muons". Chemical Physics Letters. 539: 209–221. Bibcode:2012CPL...539..209M. doi:10.1016/j.cplett.2012.04.06..

　　 [11]Moncada, F.; Cruz, D.; Reyes, A (10 May 2013). "Electronic properties of atoms and molecules containing one and two negative muons". Chemical Physics Letters. 570: 16–21. Bibcode:2013CPL...570...16M. doi:10.1016/j.cplett.2013.03.004..

　　 [12]“πμ库仑束缚态的检测”。库姆比斯、弗莱克斯、霍尔、肯涅利、Kirkby、皮乔尼、波拉特、施瓦茨、斯皮策、托拉斯卡、维斯纳、布迪克和卡斯特，列特物理学报。37，249 (1976) " Measurement of the Rate of the forming of Pi-Mu Atoms " in K _ L decent，S.H. Aronson，R.H. Bernstein，R.D. Cousins，Jr .，J.F. Greenhalgh，D. Hedin，M. Schwartz，T.K. Shea，G.B. Thomson，B. Winstein，列特物理学报。48，1078 (1982)。.

　　 [13]TRIUMF 子氢合作。“μ子氢研究简述”。检索于 2010-11-7.

　　 [14]Antognini, A.; Nez, F.; Schuhmann, K.; Amaro, F. D.; Biraben, F.; Cardoso, J. M. R.; Covita, D. S.; Dax, A.; Dhawan, S.; Diepold, M.; Fernandes, L. M. P.; Giesen, A.; Gouvea, A. L.; Graf, T.; Hänsch, T. W.; Indelicato, P.; Julien, L.; Kao, C. -Y.; Knowles, P.; Kottmann, F.; Le Bigot, E. -O.; Liu, Y. -W.; Lopes, J. A. M.; Ludhova, L.; Monteiro, C. M. B.; Mulhauser, F.; Nebel, T.; Rabinowitz, P.; Dos Santos, J. M. F.; Schaller, L. A. (2013). "Proton Structure from the Measurement of 2S-2P Transition Frequencies of Muonic Hydrogen". Science. 339 (6118): 417–420. Bibcode:2013Sci...339..417A. doi:10.1126/science.1230016. hdl:10316/79993. PMID 23349284..

　　 [15]Mohr, Peter J.; Newell, David B.; Taylor, Barry N. (2015). "CODATA recommended values of the fundamental physical constants: 2014". Zenodo. arXiv:1507.07956. doi:10.5281/zenodo.22827..

　　 [16]Wood, B. (3–4 November 2014). "Report on the Meeting of the CODATA Task Group on Fundamental Constants" (PDF). BIPM. p. 7..

　　 [17]Carlson, Carl E. (May 2015). "The Proton Radius Puzzle". Progress in Particle and Nuclear Physics. 82: 59–77. arXiv:1502.05314. Bibcode:2015PrPNP..82...59C. doi:10.1016/j.ppnp.2015.01.002..

　　 [18]"The Muon g-2 Experiment Home Page". G-2.bnl.gov. 2004-01-08. Retrieved 2012-01-06..

　　 [19]"(from the July 2007 review by Particle Data Group)" (PDF). Retrieved 2012-01-06..

　　 [20]Hagiwara, K; Martin, A; Nomura, D; Teubner, T (2007). "Improved predictions for g−2g−2 of the muon and αQED(MZ2)". Physics Letters B. 649 (2–3): 173–179. arXiv:hep-ph/0611102. Bibcode:2007PhLB..649..173H. doi:10.1016/j.physletb.2007.04.012..

　　 [21]"Revolutionary muon experiment to begin with 3,200-mile move of 50-foot-wide particle storage ring". May 8, 2013. Retrieved Mar 16, 2015..

　　 [22]"Decision Sciences Corp"..

　　 [23]George, E.P. (July 1, 1955). "Cosmic rays measure overburden of tunnel". Commonwealth Engineer: 455..

　　 [24]Alvarez, L.W. (1970). "Search for hidden chambers in the pyramids using cosmic rays". Science. 167 (3919): 832–9. Bibcode:1970Sci...167..832A. doi:10.1126/science.167.3919.832. PMID 17742609..

　　 [25]Morishima, Kunihiro; Kuno, Mitsuaki; Nishio, Akira; Kitagawa, Nobuko; Manabe, Yuta (2017). "Discovery of a big void in Khufu's Pyramid by observation of cosmic-ray muons". Nature. 422 (6929): 386–390. arXiv:1711.01576. Bibcode:2017Natur.422..277B. doi:10.1038/nature24647. PMID 29160306..

　　 [26]Borozdin, Konstantin N.; Hogan, Gary E.; Morris, Christopher; Priedhorsky, William C.; Saunders, Alexander; Schultz, Larry J.; Teasdale, Margaret E. (2003). "Radiographic imaging with cosmic-ray muons". Nature. 422 (6929): 277. Bibcode:2003Natur.422..277B. doi:10.1038/422277a. PMID 12646911..

　　 [27]决策科学公司授予东芝福岛第一核电站综合项目合同。。决策科学(2014 年 8 月 8 日).

　　 [28]东京电力公司将在 2 月初使用 muon 《福岛日记》(2015 年 1 月)开始 “扫描” 1 号反应堆内部.

　　 [29]"Muon measuring instrument production for "muon permeation method" and its review by international experts". IRID.or.jp..

　　 [30]μ子扫描从福岛第一核电站开始–简单地说.