量子力学

                     

贡献者： 待更新

　　 （本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

　　 量子力学（英语：quantum mechanics；或称量子论）是描述微观物质（原子、亚原子粒子）行为的物理学理论，量子力学是我们理解除万有引力之外的所有基本力（电磁相互作用、强相互作用、弱相互作用）的基础。

　　 量子力学是许多物理学分支的基础，包括电磁学、粒子物理、凝聚态物理以及宇宙学的部分内容。量子力学也是化学键理论、结构生物学以及电子学等学科的基础。

　　 量子力学主要是用来描述微观下的行为，所描述的粒子现象无法精确地以经典力学诠释。例如：根据哥本哈根诠释，一个粒子在被观测之前，不具有任何物理性质，然而被观测之后，依测量仪器而定，可能观测到其粒子性质，也可能观测到其波动性质，或者观测到一部分粒子性质一部分波动性质，此即波粒二象性。

　　 量子力学始于 20 世纪初马克斯·普朗克和尼尔斯·玻尔的开创性工作，马克斯·玻恩于 1924 年创造了 “量子力学” 一词。因其成功的解释了经典力学无法解释的实验现象，并精确地预言了此后的一些发现，物理学界开始广泛接受这个新理论。量子力学早期的一个主要成就是成功地解释了波粒二象性，此术语源于亚原子粒子同时表现出粒子和波的特性。

1. 历史

　　 对光的波动性研究始于 17 世纪和 18 世纪，当时像罗伯特·胡克(Robert Hooke)、克里斯蒂安·惠更斯(Christiaan Huygens)和莱昂哈德·欧拉(Leonhard Euler)这样的科学家根据实验观察提出了光的波动说。[1] 1803 年，英国博学家托马斯·杨( Thomas Young)在一篇题为 光和颜色的本质的论文中描述了他的著名的双缝实验。这个实验在人们普遍接受光的波动说教方面发挥了重要作用。

　　 1838 年，麦可·法拉第(Michael Faraday)发现了阴极射线。在此之后是 1859 年古斯塔夫·基尔霍夫(Gustav Kirchhoff)关于黑体辐射问题的陈述，1877 年路德维希·玻尔兹曼(Ludwig Boltzmann)关于物理系统的能量状态可以是分立的设想，以及 1900 年马克斯·普朗克的量子假说。[2] 普朗克关于能量以分立的 “量子”(或能量包)辐射和吸收的假设与观测到的黑体辐射模式精确匹配。

　　 1896 年，威廉·维恩凭(Wilhelm Wien)经验确定了黑体辐射的分配定律，[3] 以他的名字被称为维恩定律，从麦克斯韦方程组的角度考虑，路德维希·玻尔兹曼(Ludwig Boltzmann)也独立地得出了这个结果。然而，它只在高频部分有效，而低估了低频辐射。后来，普朗克利用玻尔兹曼对热力学的统计解释修正了这个模型，并提出了现在所谓的黑体辐射定律，这进一步推动了量子力学的发展。

　　 继马克斯·普朗克于 1900 年解决了黑体辐射问题(1859 年报道)之后，阿尔伯特·爱因斯坦提出了一个基于量子的理论来解释光电效应(1905 年，1887 年报道)的想法。大约在 1900-1910 年，原子理论和光的微粒理论[4] 第一次被广泛接受为科学事实；后一种理论可以分别视为物质的量子理论和电磁辐射的量子理论。

　　 最先研究自然界量子现象的是阿瑟·康普顿(Arthur Compton)、钱德拉塞卡拉·拉曼( C. V. Raman)和皮特·塞曼(Pieter Zeeman)，他们每个人都有以他们名字命名的量子效应。罗伯特·安德鲁·密立根(Robert Andrews Millikan)通过实验研究了光电效应，阿尔伯特·爱因斯坦为此发展了一套理论。与此同时，欧内斯特·卢瑟福(Ernest Rutherford)通过实验发现了原子的核模型，为此，尼尔斯·玻尔(Niels Bohr)发展了他的原子结构理论，后来得到了亨利·莫塞莱(Henry Moseley)实验的证实。1913 年，彼得·约瑟夫·威廉·德拜(Peter Debye)进一步发展了尼尔斯·玻尔的原子结构理论，引入了椭圆轨道，这一概念也是由阿诺·索末菲(Arnold Sommerfeld)提出的。[5] 这个阶段被称为旧量子论。

　　 根据普朗克的理论，每个能量元($E$)与其频率成比例($\nu$):

　　 $E = h\nu$ ,

　　 其中 h 是普朗克常数。

　　 普朗克谨慎地坚持认为，这只是辐射吸收和发射过程的一个方面，与辐射本身的物理现实无关。[6] 事实上，他认为他的量子假说只是一个获得正确答案的数学把戏，而不是一个相当大的发现。[7] 然而，在 1905 年，阿尔伯特·爱因斯坦现实地解释了普朗克的量子假说，并用它来解释了光电效应，即光照射在某些材料上从材料中射出电子。他因这项工作获得了 1921 年诺贝尔物理学奖。

　　 爱因斯坦进一步发展了这一思想，表明电磁波(如光)也可以被描述为粒子(后来称为光子)，其能量的分立量子数取决于其频率。[8]

　　 量子力学的基础是在 20 世纪上半叶由马克斯·普朗克、尼尔斯·玻尔、维尔纳·海森堡、路易·德布罗意、阿瑟·康普顿、阿尔伯特·爱因斯坦、埃尔温·薛定谔、梅克斯·玻恩、约翰·冯·诺依曼、保罗·狄拉克、恩里科·费米、沃尔夫冈·泡利、马克斯·冯·劳厄、弗里曼·戴森、大卫·希尔伯特、威廉·维恩、萨特延德拉·纳特·玻色、阿诺德·索末菲等人建立。尼尔斯·玻尔的哥本哈根诠释被广泛接受。

　　 20 世纪 20 年代中期，量子力学的发展促使它成为原子物理学的标准表述。1925 年夏天，玻尔和海森堡发表的研究成果终结了旧的量子理论。在某些过程和测量中，光的量子表现出类似粒子的特性，因此光的量子被称为光子(1926)。1926 年，埃尔温·薛定谔提出了电子等粒子波函数的偏微分方程。当被限制在有限区域时，这个方程只能得到特定的解，对应于分立的量子态 -这与矩阵力学所给出的结果相同。[9] 从爱因斯坦的简单假设中，诞生了一系列的辩论、理论和测试。因此，整个量子物理领域呈现在大众面前，并且在 1927 年的第五届索尔维会议会议上被广泛接受。

　　 人们发现，亚原子粒子和电磁波既不是简单的粒子也不是波，而是各有特定的性质。这就产生了波粒二象性的概念。

　　 到了 1930 年，量子力学在戴维·希尔伯特、保罗·狄拉克和约翰·冯·诺依曼的工作下得到进一步的统一和形式化[10] 更加强调测量、我们对现实认识的统计本质以及对 “观察者” 的哲学推测。此后，它渗透到许多学科，包括量子化学、量子电子学、量子光学和量子信息科学。它的现代理论发展包括弦理论和量子引力理论。它还为现代元素周期表的许多特征提供了一个有用的框架，并描述了原子在化学键形成过程中的行为和计算机半导体中的电子流，因此在许多现代技术中起着至关重要的作用。

　　 虽然量子力学被构建来描述非常小的世界，但它也能解释一些宏观现象，如超导体，[11] 和超流体。[12]

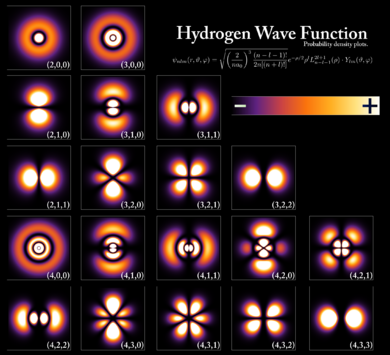
　　 量子 这个词源自拉丁语，意思是 “有多大” 或 “有多少”。[13] 在量子力学中，它指的是分配给特定物理量的分立单位，例如静止原子的能量(见图 1)。粒子是具有波状性质的分立能量包的发现导致了物理学中关于原子和亚原子系统的分支，这一分支今天被称为量子力学。它是许多物理和化学领域的数学框架的基础，包括凝聚态物理、固体物理、原子物理、分子物理学、计算物理、计算化学、量子化学、粒子物理、核化学和核物理。[14] 该理论的一些基本方面仍在积极研究中。[15]

　　 量子力学对于理解原子长度的尺度和更小尺度下的系统行为至关重要。如果一个原子的物理性质只能用经典力学来描述，那么电子就不能围绕原子核做轨道圆周运动，因为轨道上的电子发射辐射(由于圆周运动)，并且会因为能量的损失而快速的与原子核碰撞。这个理论框架无法解释原子的稳定性。相反，电子可以在绕原子核的轨道上保持不确定的、模糊的、几率波的运动，这挑战了经典力学和电磁学的传统假设。[16]

　　 量子力学最初的发展是为了更好地解释和描述原子，特别是同一化学元素的不同同位素以及亚原子粒子发出的光谱差异。简而言之，量子力学原子模型在动摇经典力学和电磁学的领域取得了惊人的成功。

　　 广义而言，量子力学包含经典物理学无法解释的四类现象:

• 某些物理性质的量子化
• 量子纠缠
• 不确定性原理
• 波粒二象性

　　 然而，后来在 2018 年 10 月，有物理学家研究称，对于单粒子，量子行为可以用经典物理学来解释，但对于多个粒子，如量子纠缠和相关的非定域现象则不能。[17][18]

2. 数学公式

　　 在由保罗·狄拉克[19]、戴维·希尔伯特、[20] 约翰·冯·诺依曼、[21] 还有赫尔曼·外尔发展的量子力学的严谨数学表述中，[22] 量子力学系统的可能状态是被符号化的，[23] 作为单位矢量(称为 态矢)中。形式上，它们位于复可分希尔伯特空间中 –该空间被称为系统的态矢空间或关联希尔伯特空间 –可被良好定义复数范数为 1(相位因子)。换句话说，可能的状态是希尔伯特空间投影空间中的点，通常称为复投影空间。希尔伯特空间的确切性质取决于系统 –例如，位置和动量状态的态空间是平方可积函数的空间，而单个质子自旋的状态空间只是两个复平面的乘积。每一个可观测值都由作用在态空间上的最大厄米(精确地说:自伴)线性算符表示。可观测值的每个本征态对应于算符的一个本征向量，相关的本征值对应于该本征态的可观测值。如果算符的谱是分立的，则可观测值只能获得这些分立的特征值。

　　 在量子力学的形式中，系统在给定时间的状态由复波函数描述，也称为复向量空间中的态向量。[24] 这个抽象的数学对象允许计算具体实验结果的概率。例如，它允许计算在特定时间在原子核周围的特定区域找到电子的概率。与经典力学相反，人们永远无法以任意精度同时预测共轭物理量，如位置和动量。例如，电子可以被认为(以一定的概率)位于给定空间区域内的某处，但它们的确切位置未知。恒定概率密度的轮廓，通常被称为 “云”，可以在原子核周围绘制，用以概念化电子最有可能的位置。海森堡的不确定性原理量化了由于粒子的共轭动量而无法精确定位粒子的能力。[25]

　　 还有一种解释，作为测量的结果，包含系统概率信息的波函数从给定的初态坍缩为特定的本征态。测量的可能结果是代表可观测值的算符的本征值 –这解释了为什么选择厄米算符，因为所有特征值都是实数。给定状态下可观测值的概率分布可以通过计算相应算符的谱分析得到。海森堡不确定性原理由对应于某些可观察量的算符的不对易来表示。

　　 因此，量子力学的概率性质源于测量行为。这是量子系统最难理解的方面之一。这是著名的玻尔-爱因斯坦之争的中心话题，两位科学家试图通过思想实验来阐明这些基本原则。在量子力学形成后的几十年里，什么是 “测量” 的问题已经得到了广泛的研究。量子力学的新解释已经被公式化，不再使用 “波函数坍缩” 的概念。其基本思想是，当一个量子系统与一个测量仪器相互作用时，它们各自的波函数会纠缠在一起，从而原始的量子系统不再作为一个独立的实体存在。[26]

　　 一般来说，量子力学不会给出确定的值。相反，它使用概率分布进行预测；也就是说，它描述了测量一个可观测值获得可能结果的概率。通常，这些结果会受到许多因素的影响，比如密集的概率云。概率云是近似的(但比玻尔模型更好)模拟，其中电子位置由概率函数即波函数特征值给出，这样概率就是复振幅模的平方，或量子态核吸引。[27][28] 自然，这些概率将取决于测量 “瞬间” 的量子态。因此，所得到值也有不确定性。然而，某些态与特定可观察值的确定值相关。这些被称为可观测的本征态(“本征” 可以从德语翻译为 “固有” 或 “特征”)。[29]

　　 在日常生活中，将一切(所有可观察到的)都视为本征态是自然和直观的。一切似乎都有明确的位置、明确的动量、明确的能量和明确的发生时间。然而，量子力学并不能同时精确地指出一个粒子的位置和动量(因为它们是共轭对)或者能量和时间(因为它们也是共轭对)的精确值。相反，它只提供了一个概率范围，在这个范围内，粒子可能被赋予动量和动量概率。因此，用不同的词来描述具有不确定值的态和具有确定值的态(本征态)是有用的。

　　 通常，系统不会处于我们感兴趣的可观察(粒子)的本征态。然而，如果测量可观测值，波函数将瞬时成为该可观测值的本征态(或 “广义” 本征态)。这个过程被称为波函数坍缩，这是一个备受争议的过程[30] 这包括所涉及正在研究的系统，也包括测量设备。如果在测量之前知道相应的波函数，就能计算出波函数坍缩成每个可能的本征态的概率。

　　 例如，上例中的自由粒子通常具有一个波函数，它是一个以某个平均位置 x0 (既不是位置的本征态，也不是动量的本征态)为中心的波包。当我们测量粒子的位置时，不可能确定地预测结果。[26] 很可能，但不确定，它会在 x0 附近波函数的振幅很大。测量完成后，获得了结果 x，波函数在 x 处坍缩成一个本征态。[31]

　　 量子态的时间演化由薛定谔方程描述，其中哈密顿量(对应于系统总能量的算符)随时间演化。波函数的时间演化是确定的，在这个意义上，给定一个波函数在初始时刻的样子，就能对以后的任何时刻的波函数做出确定的预测。[32]

　　 另一方面，在测量期间，初始波函数变成另一个，以后的波函数是不确定的，它是不可预测的(即随机的)。[33][34]

　　 波函数随着时间的推移而变化。薛定谔方程描述了波函数是如何随时间变化的，与在经典力学中的牛顿第二定律扮演着相似的角色。将薛定谔方程应用在前面提到的自由粒子例子上进行预测，波包的中心将以恒定的速度在空间中移动(就像一个没有作用力的经典粒子)。然而，波包也会随着时间的推移而向外扩散，这意味着位置会随着时间的推移而变得更加不确定。这还具有将位置本征态(可以被认为是无限尖锐的波包)转变成不再代表(确定的，确定的)位置本征态的加宽波包的效果。[35]

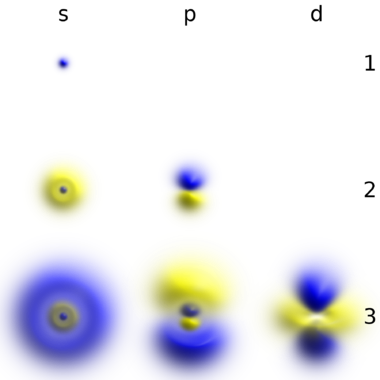
　　 一些波函数产生的概率分布是常数，或者与时间无关 –例如，当处于恒定能量的静止状态时，时间在波函数的绝对值平方中消失。许多在经典力学中被动态处理的系统被这样的 “静态” 波函数所描述。例如，未激发原子中的单个电子在经典力学中被描述为围绕原子核做圆形轨迹运动的粒子，而在量子力学中，它被描述为围绕原子核的静态球对称波函数(图一)(请注意，只有最低角动量状态，标记为 $s$，球对称)。[36]

　　 薛定谔方程作用于整个几率幅，不仅仅是它的绝对值。尽管几率幅的绝对值传递了概率信息，但它的相位传递了量子态之间的干涉信息。这导致了量子态的 “波状” 行为。事实证明，只有极少数相对简单的哈密顿算符可以得到薛定谔方程的解析解，其中最重要的代表是量子谐振子、势箱中粒子、二氢阳离子和氢原子。甚至氦原子都不可以 –它只比氢原子多一个电子 –就破坏了所有试图得到解析解的尝试。

　　 然而，有几种得到近似解的技术。在被称为微扰理论的重要方法中，人们使用简单量子力学模型的解析结果来生成与简单模型相关的更复杂模型的结果，例如通过添加弱势能。另一种方法是 “半经典运动方程” 方法，它适用于量子力学只对经典行为产生微弱(小)偏差的系统。然后可以根据经典运动学计算这些偏差。这种方法在量子混沌领域尤为重要。

3. 量子力学的等价数学表述

　　 量子力学有许多数学上等价的表述。最古老和最常用的表述之一是由保罗·狄拉克提出的 “变换理论”，它统一和推广了量子力学的两个最早的表述 –矩阵力学(由维尔纳·海森堡建立)和波动力学(由埃尔温·薛定谔建立)。[37]

　　 特别是自从 1932 年海森堡因发展量子力学而被授予诺贝尔物理学奖以来，直到 1954 年马克斯·玻恩获得诺贝尔奖，玻恩在量子力学发展中的作用一直被忽视。玻恩在 2005 年出版的一本传记中提到了这个问题，这本传记叙述了他在量子力学的矩阵表述和概率幅的使用方面所扮演的角色。海森堡本人也承认，他从玻恩那里学到了矩阵力学，并在 1940 年马克斯·普朗克(Max Planck)的纪念文集上发表了这篇文章。[38] 在矩阵表述中，量子系统的瞬时状态传递了其可测量属性或 “可观测量” 的概率。可观测的例子包括能量、位置、动量和角动量。可观测量可以是连续的(例如粒子的位置)，也可以是分立的(例如电子与氢原子结合的能量)。[39] 量子力学的另一种表述是费曼路径积分表述，其中量子力学振幅被认为是初态和末态之间所有可能的经典和非经典路径的总和。这是经典力学中作用量原理的量子力学对应。

4. 与其他科学理论的互动

　　 量子力学的规则是基础性的。量子力学要求一个系统的态空间是希尔伯特空间(重要的是，该空间有内积)，并且该系统的可观测量是厄米算符作用于该空间中的向量得到的，尽管它们没有告诉我们哪个希尔伯特空间或哪个算符。为了获得量子系统的定量描述，可以适当地选择这些空间以及算符。作出这些选择的一个重要原则是对应原理，该原理指出，当一个系统移动到更高的能量或等价于更大的量子数时，量子力学的预测逐渐接近经典力学的预测，即当单个粒子表现出一定程度的随机性时，在包含数百万粒子的系统中，展现出统计平均效果，并且在高能量极限时，随机行为的统计概率接近零。换句话说，经典力学只是大系统的量子力学。这种 “高能” 极限被称为 经典的 或者 对应极限。人们甚至可以从建立一个特定系统的经典模型开始，然后尝试猜测在对应极限中产生经典模型的潜在量子模型。

　　 当量子力学最初被公式化时，它被应用于对应极限是非相对论经典力学。例如，众所周知的量子谐振子模型对振子的动能使用了明确的非相对论表达式，因此是经典谐振子的量子版本。

　　 早期将量子力学与狭义相对论结合起来的尝试包括用协变方程(如克莱因-戈尔登方程方程或狄拉克方程)代替薛定谔方程方程。虽然这些理论成功地解释了许多实验结果，但由于忽略了相对论允许粒子的产生和湮灭，因此它们具有某些不令人满意的性质。一个完全相对论性的量子理论需要量子场论的发展，量子场论将量子化应用于一个场(而不是一组固定的粒子)。第一个完整的量子场论，量子电动力学，包含了电磁相互作用的完整量子描述。描述电动力学系统通常不需要量子场论的完整框架。一种更简单的方法是将带电粒子视为受经典电磁场作用的量子力学物体，这种方法自量子力学诞生以来就一直被采用。例如，氢原子的基本量子模型使用经典的 $-{e^2}/(4 \pi \epsilon_{0} r)$ 库仑势。如果电磁场中的量子涨落发挥重要作用，例如带电粒子发射光子，这种 “半经典” 方法就会失败。

　　 应用于强相互作用力和弱相互作用力的量子场论也得到了发展。强力的量子场论被称为量子色动力学，描述了夸克和胶子等亚核粒子的相互作用。物理学家阿卜杜勒·萨拉姆、谢尔登·格拉肖和史蒂芬·温伯格将量子化形式的弱核力和电磁力统一为一个量子场论(称为电弱理论)。这三个人因为这项工作分享了 1979 年的诺贝尔物理学奖。[40]

　　 事实证明，很难建立引力的量子模型，引力是未被量子化的基本力。半经典近似是可行的，可以得到霍金辐射等预测。然而，一个完整的量子引力理论的形成受到广义相对论(目前已知的最精确的引力理论)和量子理论的一些基本假设之间明显不相容的阻碍。解决这些不相容性是一个活跃的研究领域，弦理论等理论是未来量子引力理论的可能理论之一。

　　 经典力学也被扩展到复域，复域的经典力学表现出与量子力学相似的行为。[41]

4.1 量子力学和经典物理学

　　 量子力学的预测已经通过得到了非常高精度的实验验证。[42] 根据经典力学和量子力学的对应原理，所有的物体都遵守量子力学的定律，而经典力学只是大系统物体(或大粒子集合的量子统计力学)的近似。[43] 因此，经典力学的定律是在大系统或大量子数的极限下，以统计平均值的形式从量子力学的定律中推导出来的。[44] 然而，混沌系统没有良好的量子数，量子混沌研究的就是这些系统中经典描述和量子描述之间的关系。

　　 量子相干是经典理论和量子理论之间的本质区别，爱因斯坦-波多尔斯基-罗森(EPR)悖论就是通过对局部实在论对量子力学的某种哲学解释的攻击，说明了这一点。[45] 量子干涉包括几率幅相加，而经典的 “波” 是 强度相加。对于微观物体，系统的尺度远小于相干长度，这就导致了量子系统的长程纠缠等非局域现象。[46] 量子相干在宏观尺度上通常不明显，尽管这一规则可以在极低的温度下(即接近绝对零度)发生例外，在这种温度下量子行为可以在宏观上表现出来。[47] 这符合以下观察结果:

• 经典系统的许多宏观性质是其各部分量子行为的直接结果。例如，大块物质的稳定性(仅由在电磁力作用下会迅速坍塌的原子和分子组成)、固体的刚性以及物质的机械、热、化学、光学和磁性都是电荷在量子力学规则下相互作用的结果。[48]
• 当处理极小尺寸或接近光速的粒子时，量子力学和相对论所假设的物质的看似 “奇异” 的行为变得更加明显，但经典的、通常被认为是 “牛顿” 的物理定律仍然能够准确地预测绝大多数 “大” 物体(在大分子或更大的数量级)在远小于光速的速度下的行为。[49]

4.2 量子运动学和经典运动学的哥本哈根诠释

　　 经典力学和量子力学的一大区别在于，它们使用了非常不同的运动学描述。[50]

　　 在尼尔斯·玻尔成熟的观点中，量子力学现象需要做实验，对系统的所有设备进行完整的描述，包括准备、媒介和最终测量。这些描述是宏观的，用一般语言表达，辅以经典力学的概念。[51][52][53][54] 系统的初始条件和最终条件分别由位形空间中的值来描述，例如位置空间或一些等价空间，例如动量空间。量子力学不允许同时从位置和动量两个方面对初始条件或 “状态”(经典意义上的状态)进行完全精确的描述，以支持对最终条件的精确确定性和因果预测。[55][56] 在这个意义上，玻尔在他成熟的著作中主张，量子现象是一个过程，一个从初态到末态的过程，而不是经典意义上的瞬时 “状态”。[57][58] 因此，在量子力学中有两种过程：平稳过程和过渡过程。对于一个平稳过程来说，初始条件和最终条件是一样的。对于过渡来说，它们是不同的。显然，根据定义，如果只给出初始条件，则过程是不确定的。[55] 给定它的初始条件，预测它的最终条件是可能的，因果的，但只是概率的，因为对于波函数的演化，薛定谔方程是确定的，但波函数只是概率的描述系统。[59][60]

　　 对于许多实验，可以将系统的初始和最终条件视为粒子。在某些情况下，粒子从初态到末态可能有几个空间上不同的路径或轨迹。量子运动学描述的一个重要特征是，它不允许对这些路径中的哪一个被实际遵循做出唯一明确的陈述。只有初始条件和最终条件是确定的，并且如前一段所述，它们仅在位形空间描述或其等同物允许的情况下被精确定义。在每一种需要量子运动学描述的情况下，这种运动精度的限制总是有令人信服的原因。这种原因的一个例子是，要通过实验发现一个粒子在一个确定的位置，它必须保持不动；要通过实验发现它有一个确定的动量，它必须有自由运动；这两者在逻辑上是不相容的。[61][62]

　　 经典运动学并不主要要求对其现象进行实验描述。它允许通过相空间中的值、位形和动量空间的笛卡儿积来完全精确地描述瞬时状态。这种描述只是假设或想象一个状态是一个物理上存在的实体，而不考虑它的实验可测量性。这种对初始条件的描述，连同牛顿运动定律，允许对最终条件进行精确的确定性和因果性预测，并具有明确的通过轨迹。哈密顿动力学可以用于此。经典运动学也允许描述类似于量子力学使用的初始和最终条件描述的过程。拉格朗日力学适用于此。[63] 对于需要考虑少量普朗克常数作用的过程，经典运动学是不够的；量子力学是必需的。

4.3 广义相对论和量子力学

　　 即使爱因斯坦的广义相对论和量子理论的定义性假设无可争议地得到了严格和重复的经验证据的支持，尽管它们在理论上并不直接相互矛盾(至少在它们的主要主张方面)，但它们被证明极难整合到一个一致的、内聚的模型中。[64]

　　 引力在粒子物理学的许多领域可以忽略不计，因此广义相对论和量子力学的统一在这些特定应用中并不是一个紧迫的问题。然而，缺乏正确的量子引力理论是物理宇宙学和物理学家寻找优雅的 “万物理论” 的一个重要问题。因此，解决两种理论之间的不一致一直是 20 世纪和 21 世纪物理学的主要目标。许多杰出的物理学家，包括斯蒂芬·霍金，多年来一直在努力寻找一种潜在的万物理论。这个万物理论不仅将亚原子物理学的不同模型结合起来，还将从一个力或现象中导出自然的四种基本力——强力、电磁力、弱力和引力。斯蒂芬·霍金最初是万物理论的信徒，在考虑哥德尔不完备性定理后，他得出结论，一个完备性定理是不可获得的，并在他 2002 年的演讲《哥德尔与物理学的终结》(Godel and the End of Physics)中如此公开地陈述了这一点。[65]

4.4 统一场论的尝试

　　 通过量子力学统一基本力的探索仍在进行。量子电动力学(或 “量子电磁学”)，它是目前(至少在微扰状态下)可以与广义相对论竞争的最精确测试的物理理论，[66][67] 已经成功地与弱核力合并成电弱力，目前正在做的工作是将电弱力和强力合并成电强力。目前的预测表明，大约在 $10^{14}$ GeV 的能量上述三种力可以融合成一个统一的场。[68] 除了这种 “大统一”，据推测，有可能将引力与其他三种规范对称性合并，预计发生在大约 $10^{19}$ GeV 的水平上。然而 – 虽然狭义相对论被简单地结合到量子电动力学中 – 推广到广义相对论这个目前描述引力的最佳理论，则尚未完全纳入量子理论。理论物理学家爱德华·威滕(Edward Witten)是研究相干的万物理论人之一。他创立了 M-理论，试图描述基于超对称的弦理论。M-理论假设，我们表面上的四维时空实际上是一个包含 10 个空间维度和 1 个时间维度的 11 维时空，尽管有 7 个空间维度——在较低能量下——是完全 “压缩”(或无限弯曲)的，不容易测量或探测。

　　 另一个流行的理论是圈量子引力(LQG)，这是由卡尔罗·罗威利首先提出的描述引力量子性的理论。它也是量子空间和量子时间的理论，因为在广义相对论中时空几何是引力的一种表现。LQG 试图融合和调整标准量子力学和标准广义相对论。该理论主要描述的是空间的物理图像，其中空间是颗粒状的。粒度是量子化的直接结果。它与电磁学量子理论中光子的粒度或原子能量的分立水平具有相同的性质。但这里是空间本身，它是离散的。更准确地说，空间可以被看作是一种非常精细的织物或有限循环 “编织” 结构的网络。这些循环网络被称为自旋结网圈。自旋结网圈随时间的演变被称为自旋泡沫。预测这个结构的大小是普朗克长度，大约是 $1.616\times10^{-35}$ m。根据理论，比这个短的长度没有意义。因此，LQG 预测不仅物质，空间本身也有原子结构。

5. 哲学含义

　　 从一开始，量子力学的许多反直觉方面和结果就引发了强烈的哲学辩论和许多解释。即使是基本问题，如马克斯·玻恩关于几率幅和概率分布的基本规则，也花了几十年时间才被社会和许多科学家所重视。理查德·费曼曾经说过，“我想我可以有把握地说，没有人理解量子力学。”[69] 根据史蒂芬·温伯格的说法，“在我看来，现在对量子力学没有完全令人满意的解释。”[70]

　　 哥本哈根诠释 -主要是由尼尔斯·玻尔和维尔纳·海森堡建立 –在它发表大约 75 年后，仍然是物理学家最广泛接受的。根据这一解释，量子力学的概率本质并不是一个最终会被决定论所取代的暂时特征，而是对经典 “因果关系” 概念的最终放弃。其中还认为，由于在不同实验情况下获得的证据的共轭性质，量子力学任何明确形式的应用必须总是参考实验安排。

　　 阿尔伯特·爱因斯坦是量子理论的创始人之一，他不接受对量子力学的一些更哲学或形而上学的解释，如对决定论和因果关系的拒绝。有句名言引用他的话说，作为对这一方面的回应，“上帝不玩骰子”。[71] 他拒绝了物理系统的状态取决于其测量的实验安排的概念。他认为自然状态本身就存在，不管它是否或如何被观察到。在这种观点下，他与当前公认的量子态定义相一致，该定义在任意选择用于表示量子态的位形空间(即观察方式)下保持不变。他还认为，在量子力学的基础上，应该有一个理论，可以彻底而直接地表达反对超距作用的规则；换句话说，他坚持局部性原理。他考虑过一种特殊的建议，即使用隐变量来消除量子力学测量的不确定性，但在理论基础上遭到了否定。他认为量子力学目前是有效的，但对量子现象不是一个完善理论。他认为，未来的替代方案将需要概念上的深刻进步，而且不会很快或很容易实现。玻尔-爱因斯坦的辩论从认识论的角度对哥本哈根诠释提出了充满活力的批评。在为自己的观点辩护时，他提出了一系列反对意见，其中最著名的被称为爱因斯坦-波多尔斯基-罗森悖论。

　　 约翰·贝尔证明了这个爱因斯坦-波多尔斯基-罗森佯谬(EPR)导致了量子力学和依赖于附加隐变量的理论之间的实验上可测试的差异。已经进行的实验证实了量子力学的准确性，从而证明量子力学不能通过添加隐变量来改进。[72] 1982 年阿兰·阿斯佩的最初实验以及此后的许多后续实验已经明确验证了量子纠缠。到 1980 年代初，实验表明这种不平等在实践中确实遭到了破坏 –所以实际上存在量子力学建议的那种相关性。起初，这些看起来只是孤立的深奥效应，但到了 20 世纪 90 年代中期，它们被引入量子信息论领域，并推动了量子密码学和量子隐形传态这样的结构。[73]

　　 然而，纠缠，如贝尔型实验所证明的，并不违反因果关系，因为没有发生信息传递。量子纠缠是量子密码学的基础，可以用于银行和政府的高安全性商业应用。。

　　 形成于 1956 年的埃弗雷特多世界解释认为量子理论描述的 全部 可能性 同时地 发生在由大部分独立的平行宇宙组成的多元宇宙中。[74] 这不是通过向量子力学引入一些 “新公理” 来实现的，而是通过 消除 波包坍缩的公理来实现的。被测系统和测量仪器(包括观察者)的所有可能的相容状态都存在于真实的物理中的 –不只是形式上的数学，像其他解释一样 –量子叠加。不同系统的相容态组合的这种叠加被称为纠缠态。虽然多元宇宙是确定性的，但我们只能感知到由概率支配的非确定性行为，因为我们只能观察到我们作为观察者居住的宇宙(即，对上述叠加的相容状态贡献)。埃弗雷特的解释与约翰·贝尔的实验完全一致，并使其直观易懂。然而，根据量子退相干理论，这些 “平行宇宙” 对我们来说永远是不可接近的。不可接近性可以理解为：一旦测量完成，被测系统就会与测量它的物理学家 和 大量的其他粒子，其中一些是光子，以光速飞向宇宙的另一端都纠缠在一起。为了证明波函数没有坍缩，我们必须将这些粒子与最初测量的系统 全部 一起返回并再次测量。这不仅完全不切实际，即使 能够 从理论上讲，这样做必须销毁任何原始测量发生的证据(包括物理学家的记忆)。根据这些贝尔测试，克莱姆(1986)阐述了他的交易解释[75] 这在为玻恩定则提供物理解释方面是独一无二的。[76] 20 世纪 90 年代末，关联量子力学作为哥本哈根诠释的现代衍生物出现。

6. 应用

　　 量子力学地在解释了我们宇宙的许多特征有着巨大的成功[77]。量子力学通常是唯一能够揭示组成所有物质形式(电子、质子、中子、光子和其他)的亚原子粒子的个体行为的理论。量子力学强烈影响了弦理论——万物理论的备选理论。

　　 量子力学对于理解单个原子如何通过共价键结合形成分子也至关重要。量子力学应用在化学中被称为量子化学。量子力学还可以通过明确显示哪些分子在能量上对其他分子有利以及所涉及的能量大小，从而定量地洞察离子和共价键的形成过程。[78] 此外，现代计算化学中的大多数计算都依赖于量子力学。

　　 在许多方面，现代技术都是在量子效应尺度下得以开展。

6.1 电子学

　　 许多现代电子设备是用量子力学设计的。例子包括激光、晶体管(以及微芯片)、电子显微镜和磁共振成像。半导体的研究导致了二极管和晶体管的发明，它们是现代电子系统、计算机和电信设备中不可缺少的部分。另一个应用是制造激光二极管和发光二极管，它们是高效光源。

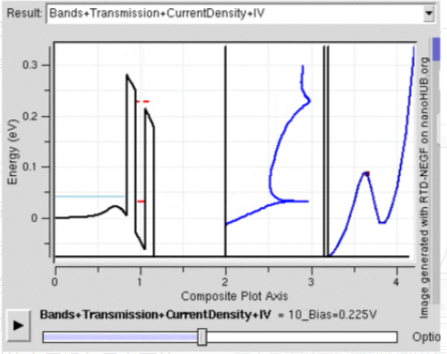
　　 许多电子器件在量子隧穿效应下工作。它甚至存在于简单的灯开关中。如果电子不能量子隧穿金属接触面上的氧化层，开关就不会工作。在 USB 驱动器中的闪存芯片使用量子隧道来擦除它们的存储的内容。一些负微分电阻效应器件也利用量子隧穿效应，例如共振隧穿二极管。与经典二极管不同，它的电流是通过两个或多个势垒的共振隧穿来传输的(见右图)。它的负电阻行为只能用量子力学来理解：当受限状态接近费米能级时，隧道电流增加。随着它的移动，电流减少。量子力学对于理解和设计这样的电子设备是必要的。

6.2 密码系统

　　 研究人员目前正在寻找直接操纵量子态的可靠方法。人们正在努力更全面地发展量子密码，这将在理论上保证信息的安全传输。

　　 与古典密码相比，量子密码术的一个固有优势是可以检测窃听。这是量子比特行为的自然结果；由于观察者的作用，如果观察到一个比特处于叠加态，叠加态就会坍缩为本征态。因为预期接收方期望以叠加状态接收比特，预期接收方就会知道有攻击，因为比特的状态将不再是叠加状态。[79]

6.3 量子计算机

　　 量子力学另一个应用目标是发展量子计算机，期望以比经典计算机快指数级的速度执行某些计算任务。量子计算机使用量子比特，而不是使用经典比特，量子比特可以是状态的叠加。量子程序员能够 为了解决经典计算无法有效解决的问题，例如搜索未排序的数据库或整数分解，量子位的叠加。IBM 声称量子计算的出现可能会推进医学、物流、金融服务、人工智能和云安全领域。[80]

　　 另一个活跃的研究课题是量子隐形传态，它涉及在任意距离传输量子信息的技术。

6.4 宏观量子效应

　　 虽然量子力学主要应用于物质和能量的较小原子体系，但一些系统在大范围内表现出量子力学效应。温度接近绝对零度时液体的无摩擦流动就是一个众所周知的例子。超导现象也是与此密切相关的，即在足够低的温度下，电子气体在导电材料(电流)中的无摩擦流动。分数量子霍尔效应是对应于长程量子纠缠模式的拓扑有序态。[81] 没有相变，具有不同拓扑顺序(或不同长程纠缠模式)的状态就不能相互改变。

6.5 量子论

　　 量子理论也为许多以前无法解释的现象提供了精确的描述，如原子中电子轨道的稳定性和黑体辐射。它还洞察了许多不同生物系统的工作原理，包括嗅觉受体和蛋白质结构。[82] 最近关于光合作用的工作也提供了证据，证明量子相关性在植物和许多其他生物体的这一基本过程中发挥着重要作用。[83] 即使如此，经典物理通常也能提供对量子物理所得结果的良好近似，通常是在有大量粒子或大量量子数的情况下。由于经典公式比量子公式简单得多，计算也容易得多，所以当系统足够大，使量子力学的影响变得微不足道时，使用经典近似是首选。

7. 例子

7.1 自由粒子

　　 例如，考虑一个自由粒子。在量子力学中，自由粒子由波函数描述。当我们测量粒子的位置和速度时，它的粒子性质就变得明显了。当我们测量粒子的波动性质，如干涉时，它的波动性质就变得明显了。波粒二象性特征被纳入量子力学表述中坐标和算符的关系中。由于粒子是自由的(不受任何相互作用的影响)，其量子态可以表示为任意形状的波，并作为波函数在空间上延伸。粒子的位置和动量是可以观察到的。不确定性原理指出，位置和动量不能同时完全精确地测量。然而，我们可以(单独)测量一个移动的自由粒子的位置，波函数在一个特定的位置 x 有一个非常大(狄拉克δ函数)的本征态，其他地方为零。如果对这样一个波函数的位置进行测量，得到 x 的概率为 100%(即完全确定性或完全精度)。这被称为位置的本征态 –或者，用数学术语来说，一个 广义位置本征态(本征分布)。如果粒子处于本征态，那么它的动量是完全未知的。另一方面，如果粒子处于动量的本征态，那么它的位置是完全未知的。[84]在具有平面波形的动量本征态中，可以表明波长等于 $h/p$，其中 $h$ 是普朗克常数和 $p$ 是本征态的动量。[85]

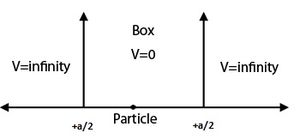
7.2 无限深方势阱

　　 一维势能箱中的粒子是数学上最简单的例子，约束导致能级的量化。势箱被定义为在某个区域内处处势能为零，因此在该区域外处处势能为无穷大。对于中的一维情况在 $X$ 方向，时间无关的薛定谔方程可以写成[86]

　　 微分算符定义为

　　 与类似前面经典动能的方程， $$\frac{1}{2m}\hat{p}_x^2 = E~$$其中态 $\psi$ 在这种情况下具有能量 $E$ 与粒子的动能一致。

　　 势箱里粒子的薛定谔方程一般解是

或者，从欧拉公式， 势箱的无限势壁决定了 $C, D,$ 和 $k$ 在 $x = 0$ 和 $x = L$ 时 $\psi$ 必须为零。因此，在 $x = 0$, 有 $D = 0.$

　　 在 $x = L$ 时，$\psi(L) = 0 = C \sin kL.$

　　 其中 $C$ 不能为零，因为这将与玻恩解释冲突。所以 $ \sin\left(kL\right) = 0,$ $kL$ 必须是 $\pi$ 的整数倍，

　　 能级的量子化也遵循对 $k$ 的约束，因为 $$E = \frac{h^2 \pi^2 n^2}{2mL^2} = \frac{n h^2}{8mL^2}~$$.

　　 粒子的基态 $n=1$，能量是 $E_1$。

　　 第 $n$ 个能级粒子的能量 $E_n = n^2 E_1, n = 2, 3, 4, \ldots$。

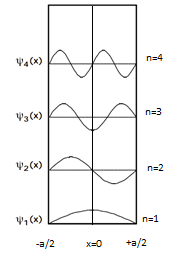
　　 粒子在势箱中的边界条件为 $-a/2 < x < +a/2$ 时 $V(x) = 0$。

　　 在这种情况下，一般的解是一样的，最终的结果会有一点变化，因为边界条件改变了 $$\psi(x) = C \sin kx + D \cos kx~.$$

　　 在 $x = 0$ 时，对于所有的 $n$，波函数都不是零。

　　 很明显，从我们得到的波函数变化图来看，

　　 在 $n = 1, 3, 4, \ldots$ 时波函数遵循以 $x = 0$ 为原点的余弦曲线

　　 在 $n = 2, 4, 6, \ldots$ 时波函数遵循以 $x = 0$ 为原点的正弦曲线

　　 从这个观察，我们可以得出波函数是正弦和余弦交替出现的结论。

　　 在这种情况下，合成的波动方程为

　　 $\psi_n(x) = A \cos\left(k_n x\right) \quad n = 1, 3, 5, \ldots$

　　 $ = B \sin\left(k_n x\right) \quad n = 2, 4, 6, \ldots$

7.3 有限深方形阱

　　 有限势阱是无限势阱问题向有限深度势阱的推广。

　　 有限势阱问题在数学上比无限势箱中粒子问题更复杂，因为波函数在势阱壁上没有固定为零。相反，波函数必须满足更复杂的数学边界条件，因为它在阱外的区域是非零的。

7.4 有限位势垒

　　 这是量子隧穿效应的模型，它在现代技术(如闪存和扫描隧道显微镜)的性能中起着重要作用。量子隧穿是涉及超晶格的物理现象的核心。

7.4 有限位势垒

　　 在经典的情况下，量子谐振子的势由下式给出 $$V(x) = \frac{1}{2}m\omega^2 x^2~$$. 这个问题可以通过直接解决薛定谔方程问题来解决，这不是小事，或者通过使用由保罗·狄拉克首先提出的更优雅的 “阶梯方法”。本征态下式给出 $$\psi_n(x) = \sqrt{\frac{1}{2^n n!}} \cdot \left(\frac{m\omega}{\pi\hbar}\right)^\frac{1}{4} \cdot e^{-\frac{m\omega x^2}{2\hbar}} \cdot H_n \left(\sqrt{\frac{m\omega}{\hbar}} x\right)~$$ 其中 $n = 0, 1, 2, \ldots$，

　　 其中 $H_n$ 是厄米项式吗 $$H_n(x) = (-1)^n e^{x^2} \frac{d^n}{dx^n} \left(e^{-x^2}\right)~,$$ 相应的能级为 $$E_n = \hbar \omega \left(n + \frac{1}{2}\right)~.$$

　　 这是另一个说明束缚态能量量子化的例子。

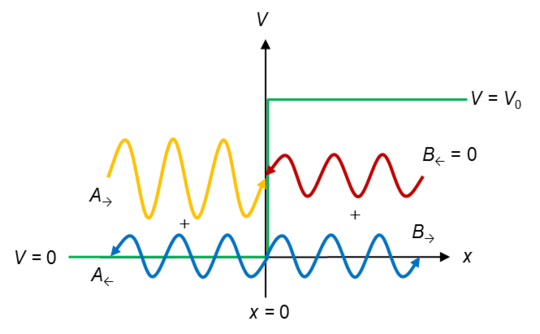
7.6 阶跃电位

　　 这种情况下的势由下式给出: $$V(x) = \begin{cases} 0, & x < 0, \\V_0, & x \geq 0\end{cases}~$$. 解的形式是左右移动波的叠加： $$\psi_1(x) = \frac{1}{\sqrt{k_1}} \left(A_{\rightarrow} e^{ik_1 x} + A_{\leftarrow} e^{-ik_1 x}\right) \quad x < 0~$$ 和 $$\psi_2(x) = \frac{1}{\sqrt{k_2}} \left(B_{\rightarrow} e^{ik_2 x} + B_{\leftarrow} e^{-ik_2 x}\right) \quad x > 0~,$$ 对解连续求导，通过边界条件确定系数 $A$ 和 $B$，其中波矢与能量的关系为 $$k_1 = \sqrt{2mE/\hbar^2} \quad \text{和} \quad k_2 = \sqrt{2m(E - V_0)/\hbar^2}~.$$ 解的每一项都可以解释为波的入射、反射或透射分量，从而可以计算透射系数和反射系数。值得注意的是，与经典力学相反，能量大于势能级的入射粒子被部分反射。

　　 笔记

1. Feynman, Richard; Leighton, Robert; Sands, Matthew (1964). The Feynman Lectures on Physics, Vol. 3. California Institute of Technology. p. 1.1. ISBN 978-0201500646.
2. Jaeger, Gregg (September 2014). "What in the (quantum) world is macroscopic?". American Journal of Physics. 82 (9): 896–905. Bibcode:2014AmJPh..82..896J. doi:10.1119/1.4878358.
3. Matson, John. "What Is Quantum Mechanics Good for?". Scientific American. Retrieved 18 May 2016.
4. The Nobel laureates Watson and Crick cited Pauling, Linus (1939). The Nature of the Chemical Bond and the Structure of Molecules and Crystals. Cornell University Press. for chemical bond lengths, angles, and orientations.
5. Max Born & Emil Wolf, Principles of Optics, 1999, Cambridge University Press
6. Mehra, J.; Rechenberg, H. (1982). The historical development of quantum theory. New York: Springer-Verlag. ISBN 978-0387906423.
7. Kragh, Helge (2002). Quantum Generations: A History of Physics in the Twentieth Century. Princeton University Press. ISBN 978-0-691-09552-3. Extract of p. 58
8. Ben-Menahem, Ari (2009). Historical Encyclopedia of Natural and Mathematical Sciences, Volume 1. Springer. ISBN 978-3540688310. Extract of p, 3678
9. E Arunan (2010). "Peter Debye" (PDF). Resonance. 15 (12): 1056–1059. doi:10.1007/s12045-010-0117-2.
10. Kuhn, T. S. (1978). Black-body theory and the quantum discontinuity 1894–1912. Oxford: Clarendon Press. ISBN 978-0195023831.
11. Kragh, Helge (1 December 2000), Max Planck: the reluctant revolutionary, PhysicsWorld.com
12. Einstein, A. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" [On a heuristic point of view concerning the production and transformation of light]. Annalen der Physik. 17 (6): 132–148. Bibcode:1905AnP...322..132E. doi:10.1002/andp.19053220607. Reprinted in The collected papers of Albert Einstein, John Stachel, editor, Princeton University Press, 1989, Vol. 2, pp. 149–166, in German; see also Einstein's early work on the quantum hypothesis, ibid. pp. 134–148.
13. Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media, Inc. p. 1056. ISBN 978-1-57955-008-0.
14. van Hove, Leon (1958). "Von Neumann's contributions to quantum mechanics" (PDF). Bulletin of the American Mathematical Society. 64 (3): Part 2:95–99. doi:10.1090/s0002-9904-1958-10206-2.
15. Feynman, Richard. "The Feynman Lectures on Physics III 21-4". California Institute of Technology. Retrieved 2015-11-24. "...it was long believed that the wave function of the Schrödinger equation would never have a macroscopic representation analogous to the macroscopic representation of the amplitude for photons. On the other hand, it is now realized that the phenomena of superconductivity presents us with just this situation.
16. Richard Packard (2006) "Berkeley Experiments on Superfluid Macroscopic Quantum Effects" Archived 11 月 25, 2015 at the Wayback Machine accessdate=2015-11-24
17. "Quantum – Definition and More from the Free Merriam-Webster Dictionary". Merriam-webster.com. Retrieved 2012-08-18.
18. Thall, Edwin. "Thall's History of Quantum Mechanics". Florida Community College at Jacksonville. Archived from the original on October 7, 2009. Retrieved May 23, 2009.
19. "ysfine.com". Retrieved 11 September 2015.
20. "Quantum Mechanics". geocities.com. 2009-10-26. Archived from the original on 2009-10-26. Retrieved 2016-06-13.
21. Staff (11 October 2018). "Where is it, the foundation of quantum reality?". EurekAlert!. Retrieved 13 October 2018.
22. Blasiak, Pawel (13 July 2018). "Local model of a qudit: Single particle in optical circuits". Physical Review. 98 (012118) (1): 012118. Bibcode:2018PhRvA..98a2118B. doi:10.1103/PhysRevA.98.012118.
23. P.A.M. Dirac, The Principles of Quantum Mechanics, Clarendon Press, Oxford, 1930.
24. D. Hilbert Lectures on Quantum Theory, 1915–1927
25. J. von Neumann, Mathematische Grundlagen der Quantenmechanik, Springer, Berlin, 1932 (English translation: Mathematical Foundations of Quantum Mechanics, Princeton University Press, 1955).
26. H.Weyl "The Theory of Groups and Quantum Mechanics", 1931 (original title: "Gruppentheorie und Quantenmechanik").
27. Dirac, P.A.M. (1958). The Principles of Quantum Mechanics, 4th edition, Oxford University Press, Oxford, p. ix: "For this reason I have chosen the symbolic method, introducing the representatives later merely as an aid to practical calculation."
28. Greiner, Walter; Müller, Berndt (1994). Quantum Mechanics Symmetries, Second edition. Springer-Verlag. p. 52. ISBN 978-3-540-58080-5., Chapter 1, p. 52
29. "Heisenberg – Quantum Mechanics, 1925–1927: The Uncertainty Relations". Aip.org. Retrieved 2012-08-18.
30. Greenstein, George; Zajonc, Arthur (2006). The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics, Second edition. Jones and Bartlett Publishers, Inc. p. 215. ISBN 978-0-7637-2470-2., Chapter 8, p. 215
31. Lodha, Suresh K.; Faaland, Nikolai M.; et al. (2002). "Visualization of Uncertain Particle Movement (Proceeding Computer Graphics and Imaging)" (PDF). Actapress.com. Archived (PDF) from the original on 2018-08-01. Retrieved 2018-08-01.
32. Hirshleifer, Jack (2001). The Dark Side of the Force: Economic Foundations of Conflict Theory. Cambridge University Press. p. 265. ISBN 978-0-521-80412-7., Chapter, p.
33. "dict.cc dictionary :: eigen :: German-English translation". dict.cc. Retrieved 11 September 2015.
34. "Topics: Wave-Function Collapse". Phy.olemiss.edu. 2012-07-27. Retrieved 2012-08-18.
35. "Collapse of the wave-function". Farside.ph.utexas.edu. Retrieved 2012-08-18.
36. "Determinism and Naive Realism : philosophy". Reddit.com. 2009-06-01. Retrieved 2012-08-18.
37. Michael Trott. "Time-Evolution of a Wavepacket in a Square Well – Wolfram Demonstrations Project". Demonstrations.wolfram.com. Retrieved 2010-10-15.
38. Michael Trott. "Time Evolution of a Wavepacket In a Square Well". Demonstrations.wolfram.com. Retrieved 2010-10-15.
39. Mathews, Piravonu Mathews; Venkatesan, K. (1976). A Textbook of Quantum Mechanics. Tata McGraw-Hill. p. 36. ISBN 978-0-07-096510-2., Chapter 2, p. 36
40. "Wave Functions and the Schrödinger Equation" (PDF). Retrieved 2010-10-15.[失效连结]
41. Rechenberg, Helmut (1987). "Erwin Schrödinger and the creation of wave mechanics" (PDF). Acta Physica Polonica B. 19 (8): 683–695. Retrieved 13 June 2016.
42. Nancy Thorndike Greenspan, "The End of the Certain World: The Life and Science of Max Born" (Basic Books, 2005), pp. 124–128, 285–826.
43. "Archived copy" (PDF). Archived from the original (PDF) on 2011-07-19. Retrieved 2009-06-04.CS1 maint: Archived copy as title (link)
44. "The Nobel Prize in Physics 1979". Nobel Foundation. Retrieved 2010-02-16.
45. Carl M. Bender; Daniel W. Hook; Karta Kooner (2009-12-31). "Complex Elliptic Pendulum". arXiv:1001.0131 [hep-th].
46. See, for example, Precision tests of QED. The relativistic refinement of quantum mechanics known as quantum electrodynamics (QED) has been shown to agree with experiment to within 1 part in 108 for some atomic properties.
47. Tipler, Paul; Llewellyn, Ralph (2008). Modern Physics (5 ed.). W.H. Freeman and Company. pp. 160–161. ISBN 978-0-7167-7550-8.
48. "Quantum mechanics course iwhatisquantummechanics". Scribd.com. 2008-09-14. Retrieved 2012-08-18.
49. Einstein, A.; Podolsky, B.; Rosen, N. (1935). "Can quantum-mechanical description of physical reality be considered complete?". Phys. Rev. 47 (10): 777. Bibcode:1935PhRv...47..777E. doi:10.1103/physrev.47.777.
50. N.P. Landsman (June 13, 2005). "Between classical and quantum" (PDF). Retrieved 2012-08-19. Handbook of the Philosophy of Science Vol. 2: Philosophy of Physics (eds. John Earman & Jeremy Butterfield).
51. (see macroscopic quantum phenomena, Bose–Einstein condensate, and Quantum machine)
52. "Atomic Properties". Academic.brooklyn.cuny.edu. Retrieved 2012-08-18.
53. http://assets.cambridge.org/97805218/29526/excerpt/9780521829526_excerpt.pdf
54. Born, M., Heisenberg, W., Jordan, P. (1926). Z. Phys. 35: 557–615. Translated as 'On quantum mechanics II', pp. 321–385 in Van der Waerden, B.L. (1967), Sources of Quantum Mechanics, North-Holland, Amsterdam, "The basic difference between the theory proposed here and that used hitherto ... lies in the characteristic kinematics ...", p. 385.
55. Dirac, P.A.M. (1930/1958). The Principles of Quantum Mechanics, fourth edition, Oxford University Press, Oxford UK, p. 5: "A question about what will happen to a particular photon under certain conditions is not really very precise. To make it precise one must imagine some experiment performed having a bearing on the question, and enquire what will be the result of the experiment. Only questions about the results of experiments have a real significance and it is only such questions that theoretical physics has to consider."
56. Bohr, N. (1939). The Causality Problem in Atomic Physics, in New Theories in Physics, Conference organized in collaboration with the International Union of Physics and the Polish Intellectual Co-operation Committee, Warsaw, May 30th – June 3rd 1938, International Institute of Intellectual Co-operation, Paris, 1939, pp. 11–30, reprinted in Niels Bohr, Collected Works, volume 7 (1933–1958) edited by J. Kalckar, Elsevier, Amsterdam, ISBN 0-444-89892-1, pp. 303–322. "The essential lesson of the analysis of measurements in quantum theory is thus the emphasis on the necessity, in the account of the phenomena, of taking the whole experimental arrangement into consideration, in complete conformity with the fact that all unambiguous interpretation of the quantum mechanical formalism involves the fixation of the external conditions, defining the initial state of the atomic system and the character of the possible predictions as regards subsequent observable properties of that system. Any measurement in quantum theory can in fact only refer either to a fixation of the initial state or to the test of such predictions, and it is first the combination of both kinds which constitutes a well-defined phenomenon."
57. Bohr, N. (1948). On the notions of complementarity and causality, Dialectica 2: 312–319. "As a more appropriate way of expression, one may advocate limitation of the use of the word phenomenon to refer to observations obtained under specified circumstances, including an account of the whole experiment."
58. Ludwig, G. (1987). An Axiomatic Basis for Quantum Mechanics, volume 2, Quantum Mechanics and Macrosystems, translated by K. Just, Springer, Berlin, ISBN 978-3-642-71899-1, Chapter XIII, Special Structures in Preparation and Registration Devices, §1, Measurement chains, p. 132.
59. Heisenberg, W. (1927). Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik, Z. Phys. 43: 172–198. Translation as 'The actual content of quantum theoretical kinematics and mechanics' here [1], "But in the rigorous formulation of the law of causality, – "If we know the present precisely, we can calculate the future" – it is not the conclusion that is faulty, but the premise."
60. Green, H.S. (1965). Matrix Mechanics, with a foreword by Max Born, P. Noordhoff Ltd, Groningen. "It is not possible, therefore, to provide 'initial conditions' for the prediction of the behaviour of atomic systems, in the way contemplated by classical physics. This is accepted by quantum theory, not merely as an experimental difficulty, but as a fundamental law of nature", p. 32.
61. Rosenfeld, L. (1957). Misunderstandings about the foundations of quantum theory, pp. 41–45 in Observation and Interpretation, edited by S. Körner, Butterworths, London. "A phenomenon is therefore a process (endowed with the characteristic quantal wholeness) involving a definite type of interaction between the system and the apparatus."
62. Dirac, P.A.M. (1973). Development of the physicist's conception of nature, pp. 1–55 in The Physicist's Conception of Nature, edited by J. Mehra, D. Reidel, Dordrecht, ISBN 90-277-0345-0, p. 5: "That led Heisenberg to his really masterful step forward, resulting in the new quantum mechanics. His idea was to build up a theory entirely in terms of quantities referring to two states."
63. Born, M. (1927). Physical aspects of quantum mechanics, Nature 119: 354–357, "These probabilities are thus dynamically determined. But what the system actually does is not determined ..."
64. Messiah, A. (1961). Quantum Mechanics, volume 1, translated by G.M. Temmer from the French Mécanique Quantique, North-Holland, Amsterdam, p. 157.
65. Bohr, N. (1928). "The Quantum postulate and the recent development of atomic theory". Nature. 121 (3050): 580–590. Bibcode:1928Natur.121..580B. doi:10.1038/121580a0.
66. Heisenberg, W. (1930). The Physical Principles of the Quantum Theory, translated by C. Eckart and F.C. Hoyt, University of Chicago Press.
67. Goldstein, H. (1950). Classical Mechanics, Addison-Wesley, ISBN 0-201-02510-8.
68. "There is as yet no logically consistent and complete relativistic quantum field theory.", p. 4. – V.B. Berestetskii, E.M. Lifshitz, L.P. Pitaevskii (1971). J.B. Sykes, J.S. Bell (translators). Relativistic Quantum Theory 4, part I. Course of Theoretical Physics (Landau and Lifshitz) ISBN 0-08-016025-5
69. "Stephen Hawking; Gödel and the end of physics". cam.ac.uk. Retrieved 11 September 2015.
70. Hawking, Stephen; Penrose, Roger (2010). The Nature of Space and Time. ISBN 978-1400834747. Retrieved 11 September 2015.
71. Tatsumi Aoyama; Masashi Hayakawa; Toichiro Kinoshita; Makiko Nio (2012). "Tenth-Order QED Contribution to the Electron g-2 and an Improved Value of the Fine Structure Constant". Physical Review Letters. 109 (11): 111807. arXiv:1205.5368v2. Bibcode:2012PhRvL.109k1807A. doi:10.1103/PhysRevLett.109.111807. PMID 23005618.
72. Parker, B. (1993). Overcoming some of the problems. pp. 259–279.
73. The Character of Physical Law (1965) Ch. 6; also quoted in The New Quantum Universe (2003), by Tony Hey and Patrick Walters
74. Weinberg, S. "Collapse of the State Vector", Phys. Rev. A 85, 062116 (2012).
75. Harrison, Edward (2000). Cosmology: The Science of the Universe. Cambridge University Press. p. 239. ISBN 978-0-521-66148-5.
76. "Action at a Distance in Quantum Mechanics (Stanford Encyclopedia of Philosophy)". Plato.stanford.edu. 2007-01-26. Retrieved 2012-08-18.
77. Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media, Inc. p. 1058. ISBN 978-1-57955-008-0.
78. "Everett's Relative-State Formulation of Quantum Mechanics (Stanford Encyclopedia of Philosophy)". Plato.stanford.edu. Retrieved 2012-08-18.
79. The Transactional Interpretation of Quantum Mechanics by John Cramer Reviews of Modern Physics 58, 647–688, July (1986)
80. The Transactional Interpretation of quantum mechanics. R.E. Kastner. Cambridge University Press. 2013. ISBN 978-0-521-76415-5. p. 35.
81. See, for example, the Feynman Lectures on Physics for some of the technological applications which use quantum mechanics, e.g., transistors (vol III, pp. 14–11 ff), integrated circuits, which are follow-on technology in solid-state physics (vol II, pp. 8–6), and lasers (vol III, pp. 9–13).
82. Pauling, Linus; Wilson, Edgar Bright (1985). Introduction to Quantum Mechanics with Applications to Chemistry. ISBN 9780486648712. Retrieved 2012-08-18.
83. Schneier, Bruce (1993). Applied Cryptography (2nd ed.). Wiley. p. 554. ISBN 978-0471117094.
84. "Applications of Quantum Computing". research.ibm.com. Retrieved 28 June 2017.
85. Chen, Xie; Gu, Zheng-Cheng; Wen, Xiao-Gang (2010). "Local unitary transformation, long-range quantum entanglement, wave function renormalization, and topological order". Phys. Rev. B. 82 (15): 155138. arXiv:1004.3835. Bibcode:2010PhRvB..82o5138C. doi:10.1103/physrevb.82.155138.
86. Anderson, Mark (2009-01-13). "Is Quantum Mechanics Controlling Your Thoughts? | Subatomic Particles". Discover Magazine. Retrieved 2012-08-18.
87. "Quantum mechanics boosts photosynthesis". physicsworld.com. Retrieved 2010-10-23.
88. Davies, P.C.W.; Betts, David S. (1984). Quantum Mechanics, Second edition. Chapman and Hall. ISBN 978-0-7487-4446-6., [https://books.google.com/books?id=XRyHCrGNstoC&pg=PA79 Chapter 6, p. 79
89. Baofu, Peter (2007). The Future of Complexity: Conceiving a Better Way to Understand Order and Chaos. Bibcode:2007fccb.book.....B. ISBN 9789812708991. Retrieved 2012-08-18.
90. Derivation of particle in a box, chemistry.tidalswan.com

8. 参考文献

　　 [1] ^Max Born & Emil Wolf, Principles of Optics, 1999, Cambridge University Press.

　　 [2] ^Mehra, J.; Rechenberg, H. (1982). The historical development of quantum theory. New York: Springer-Verlag. ISBN 978-0387906423..

　　 [3] ^Kragh, Helge (2002). Quantum Generations: A History of Physics in the Twentieth Century. Princeton University Press. ISBN 978-0-691-09552-3. Extract of p. 58.

　　 [4] ^Ben-Menahem, Ari (2009). Historical Encyclopedia of Natural and Mathematical Sciences, Volume 1. Springer. ISBN 978-3540688310. Extract of p, 3678.

　　 [5] ^E Arunan (2010). "Peter Debye" (PDF). Resonance. 15 (12): 1056–1059. doi:10.1007/s12045-010-0117-2..

　　 [6] ^Kuhn, T. S. (1978). Black-body theory and the quantum discontinuity 1894–1912. Oxford: Clarendon Press. ISBN 978-0195023831..

　　 [7] ^Kragh, Helge (1 December 2000), Max Planck: the reluctant revolutionary, PhysicsWorld.com.

　　 [8] ^Einstein, A. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" [On a heuristic point of view concerning the production and transformation of light]. Annalen der Physik. 17 (6): 132–148. Bibcode:1905AnP...322..132E. doi:10.1002/andp.19053220607. Reprinted in The collected papers of Albert Einstein, John Stachel, editor, Princeton University Press, 1989, Vol. 2, pp. 149–166, in German; see also Einstein's early work on the quantum hypothesis, ibid. pp. 134–148..

　　 [9] ^Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media, Inc. p. 1056. ISBN 978-1-57955-008-0..

　　 [10] ^van Hove, Leon (1958). "Von Neumann's contributions to quantum mechanics" (PDF). Bulletin of the American Mathematical Society. 64 (3): Part 2:95–99. doi:10.1090/s0002-9904-1958-10206-2..

　　 [11] ^Feynman, Richard. "The Feynman Lectures on Physics III 21-4". California Institute of Technology. Retrieved 2015-11-24. "...it was long believed that the wave function of the Schrödinger equation would never have a macroscopic representation analogous to the macroscopic representation of the amplitude for photons. On the other hand, it is now realized that the phenomena of superconductivity presents us with just this situation..

　　 [12] ^Richard Packard (2006) "Berkeley Experiments on Superfluid Macroscopic Quantum Effects" Archived 11 月 25, 2015 at the Wayback Machine accessdate=2015-11-24.

　　 [13] ^"Quantum – Definition and More from the Free Merriam-Webster Dictionary". Merriam-webster.com. Retrieved 2012-08-18..

　　 [14] ^Thall, Edwin. "Thall's History of Quantum Mechanics". Florida Community College at Jacksonville. Archived from the original on October 7, 2009. Retrieved May 23, 2009..

　　 [15] ^"ysfine.com". Retrieved 11 September 2015..

　　 [16] ^"Quantum Mechanics". geocities.com. 2009-10-26. Archived from the original on 2009-10-26. Retrieved 2016-06-13..

　　 [17] ^Staff (11 October 2018). "Where is it, the foundation of quantum reality?". EurekAlert!. Retrieved 13 October 2018..

　　 [18] ^Blasiak, Pawel (13 July 2018). "Local model of a qudit: Single particle in optical circuits". Physical Review. 98 (012118) (1): 012118. Bibcode:2018PhRvA..98a2118B. doi:10.1103/PhysRevA.98.012118..

　　 [19] ^P.A.M. Dirac, The Principles of Quantum Mechanics, Clarendon Press, Oxford, 1930..

　　 [20] ^D. Hilbert Lectures on Quantum Theory, 1915–1927.

　　 [21] ^J. von Neumann, Mathematische Grundlagen der Quantenmechanik, Springer, Berlin, 1932 (English translation: Mathematical Foundations of Quantum Mechanics, Princeton University Press, 1955)..

　　 [22] ^H.Weyl "The Theory of Groups and Quantum Mechanics", 1931 (original title: "Gruppentheorie und Quantenmechanik")..

　　 [23] ^Dirac, P.A.M. (1958). The Principles of Quantum Mechanics, 4th edition, Oxford University Press, Oxford, p. ix: "For this reason I have chosen the symbolic method, introducing the representatives later merely as an aid to practical calculation.".

　　 [24] ^Greiner, Walter; Müller, Berndt (1994). Quantum Mechanics Symmetries, Second edition. Springer-Verlag. p. 52. ISBN 978-3-540-58080-5., Chapter 1, p. 52.

　　 [25] ^"Heisenberg – Quantum Mechanics, 1925–1927: The Uncertainty Relations". Aip.org. Retrieved 2012-08-18..

　　 [26] ^Greenstein, George; Zajonc, Arthur (2006). The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics, Second edition. Jones and Bartlett Publishers, Inc. p. 215. ISBN 978-0-7637-2470-2., Chapter 8, p. 215.

　　 [27] ^Lodha, Suresh K.; Faaland, Nikolai M.; et al. (2002). "Visualization of Uncertain Particle Movement (Proceeding Computer Graphics and Imaging)" (PDF). Actapress.com. Archived (PDF) from the original on 2018-08-01. Retrieved 2018-08-01..

　　 [28] ^Hirshleifer, Jack (2001). The Dark Side of the Force: Economic Foundations of Conflict Theory. Cambridge University Press. p. 265. ISBN 978-0-521-80412-7., Chapter, p..

　　 [29] ^"dict.cc dictionary :: eigen :: German-English translation". dict.cc. Retrieved 11 September 2015..

　　 [30] ^"Topics: Wave-Function Collapse". Phy.olemiss.edu. 2012-07-27. Retrieved 2012-08-18..

　　 [31] ^"Collapse of the wave-function". Farside.ph.utexas.edu. Retrieved 2012-08-18..

　　 [32] ^"Determinism and Naive Realism : philosophy". Reddit.com. 2009-06-01. Retrieved 2012-08-18..

　　 [33] ^Michael Trott. "Time-Evolution of a Wavepacket in a Square Well – Wolfram Demonstrations Project". Demonstrations.wolfram.com. Retrieved 2010-10-15..

　　 [34] ^Michael Trott. "Time Evolution of a Wavepacket In a Square Well". Demonstrations.wolfram.com. Retrieved 2010-10-15..

　　 [35] ^Mathews, Piravonu Mathews; Venkatesan, K. (1976). A Textbook of Quantum Mechanics. Tata McGraw-Hill. p. 36. ISBN 978-0-07-096510-2., Chapter 2, p. 36.

　　 [36] ^"Wave Functions and the Schrödinger Equation" (PDF). Retrieved 2010-10-15.[失效连结].

　　 [37] ^Rechenberg, Helmut (1987). "Erwin Schrödinger and the creation of wave mechanics" (PDF). Acta Physica Polonica B. 19 (8): 683–695. Retrieved 13 June 2016..

　　 [38] ^Nancy Thorndike Greenspan, "The End of the Certain World: The Life and Science of Max Born" (Basic Books, 2005), pp. 124–128, 285–826..

　　 [39] ^"Archived copy" (PDF). Archived from the original (PDF) on 2011-07-19. Retrieved 2009-06-04.CS1 maint: Archived copy as title (link).

　　 [40] ^"The Nobel Prize in Physics 1979". Nobel Foundation. Retrieved 2010-02-16..

　　 [41] ^Carl M. Bender; Daniel W. Hook; Karta Kooner (2009-12-31). "Complex Elliptic Pendulum". arXiv:1001.0131 [hep-th]..

　　 [42] ^See, for example, Precision tests of QED. The relativistic refinement of quantum mechanics known as quantum electrodynamics (QED) has been shown to agree with experiment to within 1 part in 108 for some atomic properties..

　　 [43] ^Tipler, Paul; Llewellyn, Ralph (2008). Modern Physics (5 ed.). W.H. Freeman and Company. pp. 160–161. ISBN 978-0-7167-7550-8..

　　 [44] ^"Quantum mechanics course iwhatisquantummechanics". Scribd.com. 2008-09-14. Retrieved 2012-08-18..

　　 [45] ^Einstein, A.; Podolsky, B.; Rosen, N. (1935). "Can quantum-mechanical description of physical reality be considered complete?". Phys. Rev. 47 (10): 777. Bibcode:1935PhRv...47..777E. doi:10.1103/physrev.47.777..

　　 [46] ^N.P. Landsman (June 13, 2005). "Between classical and quantum" (PDF). Retrieved 2012-08-19. Handbook of the Philosophy of Science Vol. 2: Philosophy of Physics (eds. John Earman & Jeremy Butterfield)..

　　 [47] ^(see macroscopic quantum phenomena, Bose–Einstein condensate, and Quantum machine).

　　 [48] ^"Atomic Properties". Academic.brooklyn.cuny.edu. Retrieved 2012-08-18..

　　 [49] ^https://web.archive.org/web/20221109182330/http://assets.cambridge.org/97805218/29526/excerpt/9780521829526_excerpt.pdf.

　　 [50] ^Born, M., Heisenberg, W., Jordan, P. (1926). Z. Phys. 35: 557–615. Translated as 'On quantum mechanics II', pp. 321–385 in Van der Waerden, B.L. (1967), Sources of Quantum Mechanics, North-Holland, Amsterdam, "The basic difference between the theory proposed here and that used hitherto ... lies in the characteristic kinematics ...", p. 385..

　　 [51] ^Dirac, P.A.M. (1930/1958). The Principles of Quantum Mechanics, fourth edition, Oxford University Press, Oxford UK, p. 5: "A question about what will happen to a particular photon under certain conditions is not really very precise. To make it precise one must imagine some experiment performed having a bearing on the question, and enquire what will be the result of the experiment. Only questions about the results of experiments have a real significance and it is only such questions that theoretical physics has to consider.".

　　 [52] ^Bohr, N. (1939). The Causality Problem in Atomic Physics, in New Theories in Physics, Conference organized in collaboration with the International Union of Physics and the Polish Intellectual Co-operation Committee, Warsaw, May 30th – June 3rd 1938, International Institute of Intellectual Co-operation, Paris, 1939, pp. 11–30, reprinted in Niels Bohr, Collected Works, volume 7 (1933–1958) edited by J. Kalckar, Elsevier, Amsterdam, ISBN 0-444-89892-1, pp. 303–322. "The essential lesson of the analysis of measurements in quantum theory is thus the emphasis on the necessity, in the account of the phenomena, of taking the whole experimental arrangement into consideration, in complete conformity with the fact that all unambiguous interpretation of the quantum mechanical formalism involves the fixation of the external conditions, defining the initial state of the atomic system and the character of the possible predictions as regards subsequent observable properties of that system. Any measurement in quantum theory can in fact only refer either to a fixation of the initial state or to the test of such predictions, and it is first the combination of both kinds which constitutes a well-defined phenomenon.".

　　 [53] ^Bohr, N. (1948). On the notions of complementarity and causality, Dialectica 2: 312–319. "As a more appropriate way of expression, one may advocate limitation of the use of the word phenomenon to refer to observations obtained under specified circumstances, including an account of the whole experiment.".

　　 [54] ^Ludwig, G. (1987). An Axiomatic Basis for Quantum Mechanics, volume 2, Quantum Mechanics and Macrosystems, translated by K. Just, Springer, Berlin, ISBN 978-3-642-71899-1, Chapter XIII, Special Structures in Preparation and Registration Devices, §1, Measurement chains, p. 132..

　　 [55] ^Heisenberg, W. (1927). Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik, Z. Phys. 43: 172–198. Translation as 'The actual content of quantum theoretical kinematics and mechanics' here [1], "But in the rigorous formulation of the law of causality, – "If we know the present precisely, we can calculate the future" – it is not the conclusion that is faulty, but the premise.".

　　 [56] ^Green, H.S. (1965). Matrix Mechanics, with a foreword by Max Born, P. Noordhoff Ltd, Groningen. "It is not possible, therefore, to provide 'initial conditions' for the prediction of the behaviour of atomic systems, in the way contemplated by classical physics. This is accepted by quantum theory, not merely as an experimental difficulty, but as a fundamental law of nature", p. 32..

　　 [57] ^Rosenfeld, L. (1957). Misunderstandings about the foundations of quantum theory, pp. 41–45 in Observation and Interpretation, edited by S. Körner, Butterworths, London. "A phenomenon is therefore a process (endowed with the characteristic quantal wholeness) involving a definite type of interaction between the system and the apparatus.".

　　 [58] ^Dirac, P.A.M. (1973). Development of the physicist's conception of nature, pp. 1–55 in The Physicist's Conception of Nature, edited by J. Mehra, D. Reidel, Dordrecht, ISBN 90-277-0345-0, p. 5: "That led Heisenberg to his really masterful step forward, resulting in the new quantum mechanics. His idea was to build up a theory entirely in terms of quantities referring to two states.".

　　 [59] ^Born, M. (1927). Physical aspects of quantum mechanics, Nature 119: 354–357, "These probabilities are thus dynamically determined. But what the system actually does is not determined ...".

　　 [60] ^Messiah, A. (1961). Quantum Mechanics, volume 1, translated by G.M. Temmer from the French Mécanique Quantique, North-Holland, Amsterdam, p. 157..

　　 [61] ^Bohr, N. (1928). "The Quantum postulate and the recent development of atomic theory". Nature. 121 (3050): 580–590. Bibcode:1928Natur.121..580B. doi:10.1038/121580a0..

　　 [62] ^Heisenberg, W. (1930). The Physical Principles of the Quantum Theory, translated by C. Eckart and F.C. Hoyt, University of Chicago Press..

　　 [63] ^Goldstein, H. (1950). Classical Mechanics, Addison-Wesley, ISBN 0-201-02510-8..

　　 [64] ^"There is as yet no logically consistent and complete relativistic quantum field theory.", p. 4. – V.B. Berestetskii, E.M. Lifshitz, L.P. Pitaevskii (1971). J.B. Sykes, J.S. Bell (translators). Relativistic Quantum Theory 4, part I. Course of Theoretical Physics (Landau and Lifshitz) ISBN 0-08-016025-5.

　　 [65] ^"Stephen Hawking; Gödel and the end of physics". cam.ac.uk. Retrieved 11 September 2015..

　　 [66] ^Hawking, Stephen; Penrose, Roger (2010). The Nature of Space and Time. ISBN 978-1400834747. Retrieved 11 September 2015..

　　 [67] ^Tatsumi Aoyama; Masashi Hayakawa; Toichiro Kinoshita; Makiko Nio (2012). "Tenth-Order QED Contribution to the Electron g-2 and an Improved Value of the Fine Structure Constant". Physical Review Letters. 109 (11): 111807. arXiv:1205.5368v2. Bibcode:2012PhRvL.109k1807A. doi:10.1103/PhysRevLett.109.111807. PMID 23005618..

　　 [68] ^Parker, B. (1993). Overcoming some of the problems. pp. 259–279..

　　 [69] ^The Character of Physical Law (1965) Ch. 6; also quoted in The New Quantum Universe (2003), by Tony Hey and Patrick Walters.

　　 [70] ^Weinberg, S. "Collapse of the State Vector", Phys. Rev. A 85, 062116 (2012)..

　　 [71] ^Harrison, Edward (2000). Cosmology: The Science of the Universe. Cambridge University Press. p. 239. ISBN 978-0-521-66148-5..

　　 [72] ^"Action at a Distance in Quantum Mechanics (Stanford Encyclopedia of Philosophy)". Plato.stanford.edu. 2007-01-26. Retrieved 2012-08-18..

　　 [73] ^Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media, Inc. p. 1058. ISBN 978-1-57955-008-0..

　　 [74] ^"Everett's Relative-State Formulation of Quantum Mechanics (Stanford Encyclopedia of Philosophy)". Plato.stanford.edu. Retrieved 2012-08-18..

　　 [75] ^The Transactional Interpretation of Quantum Mechanics by John Cramer Reviews of Modern Physics 58, 647–688, July (1986).

　　 [76] ^The Transactional Interpretation of quantum mechanics. R.E. Kastner. Cambridge University Press. 2013. ISBN 978-0-521-76415-5. p. 35..

　　 [77] ^See, for example, the Feynman Lectures on Physics for some of the technological applications which use quantum mechanics, e.g., transistors (vol III, pp. 14–11 ff), integrated circuits, which are follow-on technology in solid-state physics (vol II, pp. 8–6), and lasers (vol III, pp. 9–13)..

　　 [78] ^Pauling, Linus; Wilson, Edgar Bright (1985). Introduction to Quantum Mechanics with Applications to Chemistry. ISBN 9780486648712. Retrieved 2012-08-18..

　　 [79] ^Schneier, Bruce (1993). Applied Cryptography (2nd ed.). Wiley. p. 554. ISBN 978-0471117094..

　　 [80] ^"Applications of Quantum Computing". research.ibm.com. Retrieved 28 June 2017..

　　 [81] ^Chen, Xie; Gu, Zheng-Cheng; Wen, Xiao-Gang (2010). "Local unitary transformation, long-range quantum entanglement, wave function renormalization, and topological order". Phys. Rev. B. 82 (15): 155138. arXiv:1004.3835. Bibcode:2010PhRvB..82o5138C. doi:10.1103/physrevb.82.155138..

　　 [82] ^Anderson, Mark (2009-01-13). "Is Quantum Mechanics Controlling Your Thoughts? | Subatomic Particles". Discover Magazine. Retrieved 2012-08-18..

　　 [83] ^"Quantum mechanics boosts photosynthesis". physicsworld.com. Retrieved 2010-10-23..

　　 [84] ^Davies, P.C.W.; Betts, David S. (1984). Quantum Mechanics, Second edition. Chapman and Hall. ISBN 978-0-7487-4446-6., [https://books.google.com/books?id=XRyHCrGNstoC&pg=PA79 Chapter 6, p. 79.

　　 [85] ^Baofu, Peter (2007). The Future of Complexity: Conceiving a Better Way to Understand Order and Chaos. Bibcode:2007fccb.book.....B. ISBN 9789812708991. Retrieved 2012-08-18..

　　 [86] ^Derivation of particle in a box, chemistry.tidalswan.com.