量子纠缠
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译)
量子纠缠(quantum entanglement),也译作量子缠结,由爱因斯坦、波多尔斯基、罗森于 1935 年提出,量子纠缠描述了两个或多个互相纠缠的粒子之间的一种 “神秘” 的关联,即使各自相隔距离很遥远,之间也没有任何介质,但是其中一个粒子的行为将会影响到另一个粒子的状态,假设其中的一个粒子被操作而自身的状态发生了变化,其中的另外一个粒子也会发生相应的变化。是经典力学无法解释的。
量子纠缠被认为是量子形式论中最非经典的特征,在量子信息科学中起着至关重要的作用。
1. 历史
1935 年,爱因斯坦、波多尔斯基和罗森三人联名在《物理学评论》杂志上发表了标志着第三次论战 的重要檄文: “能认为量子力学对物理实在的描述是完备的吗?”,并且将这篇论文发表于 5 月份的《物理评论》。[1] 这是最早探讨量子力学理论对于强关联系统所做的反直觉预测的一篇论文。这篇檄文是从经典实在论的立场出发,来论证量子力学对实在的描述是不完备的。论文发表不久,薛定谔就写信给爱因斯坦说,读到 EPR 论文非常高兴,认为这篇文章抓住了教条的量子力学的辫子。爱因斯坦在回信中写道,“你是惟一一个 我愿意与之交换意见的人。其他的同行在看问题时几乎都不是从现象到理论,而是从理论到现象,他们无法从已接受的概念网中跳出来,而只是在里面奇怪地蹦来蹦去。” 薛定谔在 EPR 论文的激发下,不到一个月的时间,就在德国《自然科学》杂志上发表了标题为 “量子力学的现状” 的文章,英译版发表在《美国哲学学会进展》杂志。这篇文章的目标是基于对经典观念 与量子观念的比较,进一步从理论上加深对量子力学深层问题的理解。在德文版的 “量子力学的现状” 一文发表后不久,薛定谔越来越意识到,在量子测量中,“纠缠” 概念 很重要,是量子力学的特征性质。不久之后,薛定谔发表了一篇重要论文,对于 “量子纠缠” 这术语给予定义,并且研究探索相关概念。薛定谔体会到这概念的重要性,他表明,量子纠缠不只是量子力学的某个很有意思的性质,而是量子力学的特征性质;量子纠缠在量子力学与经典思路之间做了一个完全切割。于是,1935 年 10 月,他又在《剑桥哲学学会的数学进展》杂志上发表 了一篇文章。这篇文章是用英文发表的,标题为 “对分离系统之间的概率关系的讨论”。在这篇文章 中,薛定谔继续推广 EPR 论文的讨论,第一次明确地用 “纠缠” 概念来描述 EPR 思想实验中两个曾经耦 合的粒子,分开之后彼此之间仍然维持某种关联的现象,或者说,用 “量子纠缠” 这一概念来描述复合的 微观粒子系统存在的那种难以理解的特殊关联。薛定谔在 “对分离系统之间的概率关系的讨论” 一文中开门见山地指出,当两个系统由于受外力作 用,在经过暂时的物理相互作用之后,再彼此分开时,我们无法再用它们相互作用之前各自具有的表达 式来描述复合系统的态,两个量子态通过相互作用之后,已经纠缠在一起。不管这两个量子系统分离 之后相距多远,都始终会神秘地联系在一起,其中一方发生变化,都会立即引发另一方产生相应的变化。薛定谔对这种特殊情境的另一种表达方式是: 一个整体的最有可能的知识不一定是它的所有部分的最 有可能的知识,即使这些部分可能是完全分离的,有能力拥有各自的 “最有可能的认识”。这种知识的 缺乏决不是由于这种相互作用是不能够被认识的,而是由于这种相互作用本身。可见,薛定谔提出量 子纠缠概念是为了描述量子测量的不确定性,并不是为了突出意识对测量的决定作用。如同爱因斯坦一样,薛定谔对于量子纠缠的概念并不满意,因为量子纠缠似乎违反在相对论中对于信息传递所设定的速度极限。[2] 爱因斯坦后来对量子纠缠给出了著名的嘲笑:“spukhafte Fernwirkung”,[3] 即 “鬼魅般的超距作用”。
EPR 论文很显然地引起了众多物理学者的兴趣,启发他们探讨量子力学的基础理论。但是除了这方面以外,物理学者认为这论题与现代量子力学并没有什么牵扯,在之后很长一段时间,物理学术界并没有特别重视这论题,也没有发现 EPR 论文可能有什么重大瑕疵。EPR 论文试图建立定域性隐变量理论来替代量子力学理论。1964 年,约翰·贝尔提出论文表明,对于 EPR 思想实验,量子力学的预测明显地不同于定域性隐变量理论。概略而言,假若测量两个粒子分别沿着不同轴向的自旋,则量子力学得到的统计关联性结果比定域性隐变量理论要强很多,贝尔不等式定性地给出这差别,做实验应该可以侦测出这差别。因此,物理学者做了很多检试贝尔不等式的实验。
1972 年,约翰·克劳泽与史达特·弗利曼(Stuart Freedman)首先完成这种检试实验。1982 年,阿兰·阿斯佩的博士论文是以这种检试实验为题目。他们得到的实验结果符合量子力学的预测,不符合定域性隐变量理论的预测,因此证实定域性隐变量理论不成立。但是,每一个相关实验都存在有漏洞,这造成了实验的正确性遭到质疑,在作总结之前,还需要完成更多精确的实验。[4]
这些年来,众多研究结果促成了应用这些超强关联来传递信息的可能性,从而导致了量子密码学的成功发展,最著名的有查理斯·贝内特(Charles Bennett)与吉勒·布拉萨(Gilles Brassard)发明的 BB84 协议、阿图尔·艾克特(Artur Eckert)发明的 E91 协议。
2005 年,中国科学技术大学潘建伟、彭承志等研究人员的小组在合肥创造了 13 公里的自由空间双向量子纠缠 “拆分”、发送的世界纪录,同时验证了在外层空间与地球之间分发纠缠光子的可行性。
2007 年开始,中国科大——清华大学联合研究小组在北京架设了长达 16 公里的自由空间量子信道,并取得了一系列关键技术突破,最终在 2009 年成功实现了世界上最远距离的量子态隐形传输,证实了量子态隐形传输穿越大气层的可行性,为未来基于卫星中继的全球化量子通信网奠定了可靠基础。该成果已经发表在 2010 年 6 月 1 日出版的英国《自然》杂志子刊《自然·光子学》上,并引起了广泛关注。
2017 年 6 月 16 日,于 2016 年 8 月 16 日 1 时 40 分在酒泉用长征二号丁运载火箭成功发射升空量子卫星墨子号首先成功实现两个量子纠缠光子被分发到相距超过 1200 公里的距离后,仍可继续保持其量子纠缠的状态。
2018 年 4 月 25 日,芬兰阿尔托大学教授麦卡﹒习岚帕(Mika Sillanpää)领导的实验团队成功地量子纠缠了两个独自震动的鼓膜,这实验演示出宏观的量子纠缠。每个鼓膜的宽度只有 15 微米,约为头发的宽度,是由 10 个金属铝原子制成。通过超导微波电路,在接近绝对温度(-273.15 摄氏度)下,两个鼓膜持续进行了约 30 分钟的互动。
2. 概念
2.1 纠缠的意义
纠缠系统被定义为其量子态不能作为其局部成分的态的乘积来考虑的系统;也就是说,它们不是若干个独立的粒子,而是一个不可分割的整体。在纠缠中,系统的一个组成部分不能在不考虑其他部分的情况下被完全描述。一个复合系统的状态总是可以被表示为局部成分的状态的乘积的和(或者称为叠加);如果这个叠加必有超过一个的项,那么这个状态就是纠缠的。
量子系统可以通过各种类型的相互作用纠缠在一起。对于一些可以达到实验目的的纠缠方式,请参见下面关于方法的章节。当被纠缠的粒子通过与环境的相互作用而退相干时,纠缠便被打破;例如,这可以发生在进行测量的时候。[5]
纠缠的一个例子是:亚原子粒子衰变为其他粒子的纠缠对。衰变事件遵循各种守恒定律,因此,对一个子粒子的测量结果必定与对另一个子粒子的测量结果高度相关(从而使得总动量、总角动量、总能量等在这个过程前后大致保持不变)。例如,一个自旋为零的粒子可以衰变为一对自旋为 1/2 的粒子。由于衰变前后的总自旋必须为零(角动量守恒),所以当第一个粒子在某个轴上被测量为自旋向上时,另一个粒子在同一轴上总会被测量到自旋向下。(这被称为自旋反相关情况;如果测量到每个自旋的先验概率相等,则称这一对粒子出于单重态)。
如果我们把这两个粒子分开,就能更好地观察到纠缠的特殊性质。让我们把其中一个放在华盛顿的白宫,另一个放在白金汉宫(把这当成一个思想实验而不是一个真实的实验)。现在,如果我们测量其中一个粒子的某个特定特征(例如自旋)并得到一个结果,然后使用相同的标准去测量另一个粒子(沿着相同轴的自旋),我们发现第二个粒子的测量结果将与第一个粒子的测量结果(在互补的意义上)相匹配,因为它们的值将是相反的。
上述结果可能让人感到惊讶,也可能不让人感到惊讶。基于经典力学和量子力学中的角动量守恒,经典系统将显示相同的性质,并且肯定需要一个隐变量理论来达到这个结果。区别在于,经典系统对所有可观察量都有明确的值,而量子系统没有。在下面将要讨论的意义上,这里考虑的量子系统似乎获得了在对第一个粒子进行了测量的情况下沿着另一个粒子的任何轴的自旋的测量结果的概率分布。这种概率分布通常不同于不测量第一个粒子的情况。对于空间上相互分离的纠缠粒子,这个结果肯定会被认为是令人惊讶的。
2.2 悖论
关于量子纠缠的悖论是:在任何一个粒子上进行的测量显然会使得整个纠缠系统的状态发生坍缩——并且是在任何关于测量结果的信息可以传递给另一个粒子之前瞬间完成这个坍缩(假设信息不能传播得比光快),因此保证了对纠缠对中的另一部分所进行的测量的 “正确” 结果。在哥本哈根诠释中,对其中一个粒子的自旋测量的结果是纠缠粒子对整体坍缩成这样一种状态,其中每个粒子沿着测量轴都有一个确定的自旋(向上或向下)。结果是随机的,每种可能性的概率为 50%。然而,如果两个粒子的自旋沿着同一轴被测量,那么它们会被发现是反相关的。这意味着对一个粒子进行测量的随机结果似乎已经传递给了另一个粒子,因此当它也被测量时可以做出 “正确的选择”。[6]
我们可以选择测量的距离和时间使得两次测量之间的间隔是类空的,因此,任何联系这两个事件的因果效应都必须传播得比光快。根据狭义相对论的原理,任何信息都不可能在两个这样的测量事件之间传播。我们甚至不可能说哪一项测量是先发生的。对于两个间隔为类空的事件(记为 $x_{1}$ 和 $x_{2}$),存在一些惯性系满足在其中 $x_{1}$ 是先发生的,也存在其他一些惯性系满足在其中先发生的是 $x_{2}$。因此,这两个测量之间的相关性不能被解释为其中一个测量决定了另一个测量:不同的观察者会对因果的角色有不同的看法。
(事实上,甚至在没有纠缠的情况下也可能出现类似的悖论:单个粒子的位置弥散在空间中,两个相距很远的探测器试图在两个不同的地方探测粒子,它们必定立即获得适当的相关性使得它们不会同时探测到粒子。)
2.3 隐变量理论
悖论的一个可能解决方案是假设量子理论是不完整的,并且测量的结果取决于预定的 “隐藏变量”。[7] 被测粒子的状态包含一些隐藏的变量,这些变量的值从分离的那一刻起就有效地决定了自旋测量的结果。这意味着每个粒子都携带着所有需要的信息,在测量时不需要从一个粒子将信息传输给另一个粒子。爱因斯坦和其他人(见前一节)最初认为这是摆脱悖论的唯一途径,并且被接受的量子力学描述(具有随机测量结果)必定是不完整的。
2.4 对贝尔不等式的违背
然而,当我们考虑沿着不同轴(例如沿着三个形成 120 度角的轴中的任何一个)测量纠缠粒子的自旋时,隐变量理论失败了。如果(在大量成对的纠缠粒子上)进行了大量成对的这种测量,那么从统计上来说,如果局域实在论者或隐变量的观点是正确的,那么实验结果将总是满足贝尔不等式。许多实验表明测量结果并不满足贝尔不等式。然而,在 2015 年之前,所有这些实验都有漏洞问题,这些问题被物理学家认为是最重要的。[8][9] 当对纠缠粒子的测量是在移动的相对论性参考系中进行的,其中每个测量(在其自身的相对论性时间框架中)发生在另一个测量之前,测量结果保持相关。[10][11]
关于沿不同轴测量自旋的基本问题是这些测量不能同时具有确定的值――它们是不相容的,因为这些测量的最大同时精度受到不确定性原理的限制。这与经典物理学中发现的结果相反,在经典物理学中,任意数量的性质可以以任意精度同时测量。物理学家已经在数学上证明了相容的测量不能显示违反贝尔不等式的相关性,[12] 因此纠缠本质上是一种非经典的现象。
2.5 时间之谜
有物理学家建议把时间的概念看作是量子纠缠的所导致的一种涌现现象。[13][14] 换句话说,时间是一种纠缠现象,它将所有相同的时钟读数(正确准备的时钟或任何可用作时钟的物体)置于同一历史中。这是 1983 年由 Don Page 和 William Wootters 首先完全理论化的。[15] 将广义相对论和量子力学结合起来的 Wheeler–DeWitt 方程——完全不考虑时间——是在 20 世纪 60 年代提出的,1983 年 Page 和 Wootters 提出了基于量子纠缠的解的时候又被重新捡起。Page 和 Wootters 认为纠缠可以用来测量时间。[16]
2013 年,在意大利都灵的 Istituto Nazionale di Ricerca Metrologica(INRIM),研究人员对 Page 和 Wootters 的想法进行了第一次实验测试。他们的结果被诠释为证实时间对于宇宙的内部观察者来说是一种涌现现象,但是对于外部观察者来说却是不存在的,正如 Wheeler–DeWitt 方程所预测的那样。[16]
2.6 时间箭头的来源
物理学家 Seth Lloyd 说,量子不确定性会导致纠缠,这被认为是时间箭头的来源。根据 Lloyd 的说法:“时间箭头是相关性增加的箭头”,[17] 可以从因果时间箭头的角度来研究纠缠,假设对一个粒子的测量这个原因决定了对另一个粒子的测量结果这个效果。
2.7 涌现重力
基于 AdS/CFT 对偶,Mark Van Raamsdonk 提出时空是一种量子自由度的涌现现象,量子自由度纠缠并存在于时空的边界上。[18] 诱导引力可以从纠缠第一定律中涌现出来。[19][20]
3. 基本概念
实验室中最常见制备量子纠缠的方式就是衰变零自旋中性π介子,原本中性π介子衰变后会变成一个(带负电)电子和一个正电子,电子和正电子互为反物质!它们会朝着相反的方向运动,如果不去测量它们,那么这个电子和正电子的共同会形成零自旋的纠缠状态。如果观测其中一个粒子,比如电子,那么它们之间的纠缠态就会确定,导致电子和正电子都有了相反状态的自旋。如果观测电子的自旋为下,那么与之纠缠的正电子自旋必为上。零自旋的 “纠缠态” $|\psi \rangle$,是两个直积态(product state)的叠加,以狄拉克标记表示为[21] $$|\psi > = {1}/{\sqrt{2}} \left( |\uparrow >\otimes |\downarrow > - |\downarrow > \otimes |\uparrow > \right)~$$
式中 $|\downarrow \rangle \otimes,|\uparrow \rangle$ 分别表示粒子的自旋为上旋或下旋。
在圆括弧内的第一项表明,电子的自旋为上旋当且仅当正电子的自旋为下旋;第二项表明,电子的自旋为下旋当且仅当正电子的自旋为上旋。两种状况叠加在一起,每一种状况都有可能发生,不能确定到底哪种状况会发生,因此,电子与正电子纠缠在一起,形成纠缠态。假若不做测量,则无法知道这两个粒子中任何一个粒子的自旋,根据哥本哈根诠释,这性质并不存在。这单态的两个粒子相互反关联,对于两个粒子的自旋分别做测量,假若电子的自旋为上旋,则正电子的自旋为下旋,反之亦然;假若电子的自旋下旋,则正电子自旋为上旋,反之亦然。
纠缠的两个粒子在分开以前,就是耦合在一起π介子,它不向上也不向下自旋,它的自旋为零。同时π介子即不带正电也不带负电,它是电中性的。而π介子衰变成正电子和电子后,电中性被 “分裂” 成带分别带正负电的两个纠缠粒子,零自旋 “分裂” 成测量后相反方向自旋的两个纠缠粒子。
量子力学不能预测到底是哪一组数值,但是量子力学可以预言,获得任何一组数值的概率为 50
不确定性原理的维持必须倚赖量子纠缠机制。例如,设想先前的一个零自旋中性π介子衰变案例,两个衰变产物各自朝着相反方向移动,分别测量电子的位置与正电子的动量,假若量子纠缠机制不存在,则可借着守恒定律预测两个粒子各自的位置与动量,这违反了不确定性原理。由于量子纠缠机制,粒子的位置与动量遵守不确定性原理。
从以相对论性速度移动的两个参考系分别测量两个纠缠粒子的物理性质,尽管在每一个参考系,测量两个粒子的时间顺序不同,获得的实验数据仍旧违反贝尔不等式,仍旧能够可靠地复制出两个纠缠粒子的量子关联。
4. 数学表述
个单独粒子的所有状态都位于一个希尔伯特空间中,这个空间是由一组 “坐标轴” 撑起来的。就像是前面所说的由上旋和下旋两个状态 “坐标轴” 所张成的空间就囊括了所有的可能自旋态。而两个粒子的自旋态所位于的希尔伯特空间就是两个单独粒子的希尔伯特空间 “混合” 而成的。而这种混合的基本规则就是这样的:两个粒子的所有可能状态的各种组合,就构成了复合空间的 “坐标轴”。也就是说,组合而成的希尔伯特空间变成了一个四维空间,这个四维空间中混合了 A 和 B 各自的可能状态,这种混合就表现为上述的四种状态组合在 AB 复合系统的希尔伯特空间中组成一个四维的笛卡尔坐标系:它们两两垂直,且覆盖了全部的可能状态。这个 “组合” 可以简单表示为: $$H_{AB} = (|\uparrow A \uparrow B >, |\uparrow A \downarrow B >) = H_A (|\uparrow A >,|\uparrow A >) \otimes H_B (|\uparrow B >, |\uparrow B >)~$$, 这种发生在两个抽象空间间的 “乘积” 叫做张量积,设定子系统 A、B 的量子态分别为 $|\alpha > A, |\beta > B$,假若复合系统的量子态 $|\psi > AB$ 不能写为量子态 $|\alpha > A \otimes |\beta >B$, 则称这复合系统为子系统 A、B 的纠缠系统, 两个子系统 A、B 相互纠缠。
5. 非局域性和纠缠
在媒体和科普作品中,量子非局域性通常被描述为等同于纠缠。虽然这对于纯二分量子态是正确的,但一般来说纠缠只对非局域关联是必要的,另外还存在不产生这种关联的混合纠缠态。[22] 一个众所周知的例子是 Werner 态,它对于某些 $p_{\text{sym}}$ 值是纠缠的,但总是可以用局域隐变量来描述。[23] 此外,研究表明,对于整个系统任意数量的划分来说,总存在着真正纠缠但可以用局域模型来描述的态。[24] 上述关于局域模型存在的证明默认了一次只有一个量子态副本可用。如果允许各方对这些状态的许多副本进行局域测量,那么许多显然是局域的状态(例如量子比特 Werner 状态)就不再能够用局域模型描述。这尤其适用于所有可提纯态。然而,在给定足够多的副本的情况下是否所有纠缠态都变成非局域态仍是一个悬而未决的问题。[25]
简而言之,双方共享的一个态的纠缠是必要的但不足以使该态成为非局域态。重要的是要认识到纠缠更普遍地被视为一个代数概念,注意到它是非定域性以及量子隐形传态和超密集编码的先决条件,而非定域性是根据实验统计来定义的,并且与量子力学的基础和诠释有更多的关系。[26]
5.1 作为一种资源的纠缠
在量子信息论中,纠缠态被认为是一种 “资源”,即生产成本高且允许实现有价值的转换的东西。这种观点最明显的背景是 “相聚遥远的实验室”,即标记为 “A” 和 “B” 的两个量子系统,每个量子系统上我们可以执行任意的量子操作,但彼此之间不进行量子力学相互作用。唯一允许的相互作用是经典信息的交换,这种交换与最一般的局域量子操作相结合,产生了称为 LOCC 操作(局域操作和经典通信)的一类操作。这些操作不允许在系统 A 和 B 之间产生纠缠态。但是如果 A 和 B 被提供了纠缠态,那么这些纠缠态和 LOCC 操作结合起来便可以实现更大类的变换。例如,A 的一个量子比特和 B 的一个量子比特之间的相互作用可以通过如下方式来实现:首先将 A 的量子比特传送到 B,然后让它与 B 的量子比特相互作用(这现在是一个 LOCC 操作,因为两个量子比特都在 B 的实验室中)然后将量子比特传送回 A。在此过程中使用了两个量子位的两个最大纠缠态。因此,纠缠态是一种资源,能够在只有 LOCC 可用的环境中实现量子相互作用(或量子信道),但它们在这个过程中会被消耗掉。还存在其它一些在其中纠缠可以被看作是一种资源的应用,例如私人通信或区分量子态。[27]
5.2 纠缠的分类
在作为资源这方面,并不是所有的量子态都有相同的价值。为了量化这个值,我们可以使用不同的纠缠度量(见下文),为每个量子态分配一个数值。然而,用一种更粗糙的方法来比较量子态往往很有趣。这产生了不同的分类方案。大多数纠缠类别是基于使用 LOCC 或这些操作的子类是否可以将状态转换为其他状态来定义的。允许的操作集越小,分类就越精细。重要的例子有:
- 如果两个状态可以通过局域酉运算转换成彼此,那么它们被称为处于相同的 LU 类。这在通常所考虑的分类中是最精细的。同一 LU 类中的两个态对于纠缠度量具有相同的数值,并且在远程实验室设定中作为资源具有相同的价值。存在无限多种不同的 LU 类(即使在最简单的两个量子位处于纯态的情况下)。[28][29]
- 如果两个状态可以通过包括概率大于 0 的测量在内的局域运算相互转换,则它们被称为属于同一个 “SLOCC 类”(即 “随机 LOCC”)中。定性地说,同一个 SLOCC 类中的两种状态 $p_{1}$ 和 $p_{2}$ 是同样强大的(因为我可以把一个转换成另一个,然后做它允许我做的任何事情),但是因为转换过程 $p_{1}\to p_{2}$ 和转换过程 $p_{2}\to p_{1}$ 可能有不同的成功概率,于是它们不再具有同等的价值。例如,对于两个纯量子位,只存在两个 SLOCC 类:纠缠态(包含(最大纠缠的)贝尔态以及 $\left|00\right\rangle + 0.01\left|11\right\rangle $ 之类的弱纠缠态)和可分态(即 $\left|00\right\rangle$ 之类的乘积态)。[30][31]
- 除了考虑态的单个副本的转换(例如 $p_{1}\to p_{2}$),我们还可以基于多拷贝转换的可能性来定义类。例如,存在如下例子,在其中 $p_{1}\to p_{2}$ 对 LOCC 来说是不可能的,但 $p_{1}\otimes p_{1}\to p_{2}$ 却是有可能的。一个非常重要(也非常粗略)的分类是基于是否有可能将任意大数量的态 $p$ 的副本转换成至少一个纯纠缠态。拥有此属性的态被称为可提纯态。这些态是最有用的量子态,因为给定足够多的这种态,我们便可以(通过局域操作)将它们转换成任何纠缠态,从而允许用于所有可能的用途。最初令人惊讶的是,并非所有纠缠态都是可提纯的,那些不可提纯的被称为 “束缚纠缠”。[32][27]
一种不同的纠缠分类是基于态中的量子相关允许 A 和 B 做什么:我们区分纠缠态的三个子集:
- 非局域态,这种态产生了无法用局域隐变量模型来解释的相关性,从而违反了贝尔不等式;
- 可操纵态,它包含足够的相关性,使得 A 可以通过局域测量来修改(“操纵”)B 的条件约化状态,并使得 A 可以向 B 证明它们所拥有的状态确实是纠缠的;最后就是
- 那些既不是非局域的也不是可操纵的纠缠态。所有三个集合都不是空集。[33]
5.3 熵
1、定义
在经典信息论中,香农熵 $H$ 与概率分布 $p_1, \cdots, p_n$ 以下列方式相关联: $$H(p_1, \cdots, p_n) = -\sum_i p_i \log_2 p_i~$$ 由于混合态 $\rho$ 是系综的一个概率分布,这自然地导向了冯·诺伊曼熵的定义:
一般来说,可以使用 Borel 测函数计算来计算非多项式函数,例如 $\log_2(\rho)$。如果非负算子 $\rho$ 作用于有限维希尔伯特空间并具有本征值 $\lambda_1, \cdots, \lambda_n$,$\log_2(\rho)$ 便只是具有相同本征向量的算子,其本征值为 $\log_2(\lambda_1), \cdots, \log_2(\lambda_n)$。于是香农熵便为:
。
因为概率为 0 的事件不应该对熵有贡献,又由于我们有 $$\lim_{p \to 0} p \log p = 0~$$, 在这里我们约定 $0 \log\left(0\right) = 0$。这也延伸到无限维情况:如果 $\rho$ 具有如下的谱分解 $$\rho = \int \lambda dP_{\lambda}~,$$ 我们在进行下面计算时假设相同的约定 $$\rho \log_2 \rho = \int \lambda \log_2 \lambda dP_{\lambda}~.$$ 和统计力学一样,系统应该拥有的不确定性(微观状态的数量)越多,熵就越大。例如,任何纯态的熵都为零,这并不奇怪,因为纯态下的系统没有不确定性。上面讨论的纠缠态的两个子系统中的任何一个的熵是 $log(2)$(我们可以证明这是 $2\times2$ 混合态的最大熵)。
2、作为纠缠的一种度量
熵提供了一种可以用来量化纠缠的工具,尽管还存在其他的纠缠度量。[35] 如果整个系统是纯的,一个子系统的熵可以用来度量它与其他子系统的纠缠度。
对于二分纯态,约化态的冯·诺伊曼熵是纠缠的唯一度量,因为它是状态族的唯一满足纠缠度量所要求的某些公理的函数。
一个经典结果告诉我们:香农熵在且仅在均匀概率分布 $(1/n, ..., 1/n)$ 的情况下达到最大值。因此,如果 $\rho$ 的约化态是如下的对角矩阵,那么二分纯态 $\rho \in H_A \otimes H_B$ 就是一个最大纠缠态 $$\begin{pmatrix}\frac{1}{n} & & \\& \ddots & \\& & \frac{1}{n}\end{pmatrix}~$$
对于混合态,约化熵诺伊曼熵不是唯一合理的纠缠度量。
此外,信息论的定义与统计力学意义上的熵密切相关(在比较这两个定义时,我们习惯上设定玻尔兹曼常数为 $k=1$)。例如,通过 Borel 泛函计算的性质,我们可以知道对于任何酉算子 $U$,我们有 $$S(\rho) = S(U\rho U^*)~$$ 事实上,如果没有这个性质,冯·诺伊曼熵就不是良定义的。
特别地,$U$ 可以是系统的时间演化算子,即 $$\mathbf{U}(t)=\exp\left(-\frac{iHt}{\hbar}\right)~,$$ 在其中 $H$ 是系统的哈密顿量。这里熵保持不变。
过程的可逆性与所导致的熵变化有关,即过程是可逆的当且仅当它保持系统的熵不变。因此,时间箭头向热力学平衡的前进仅仅是量子纠缠的不断扩展。[36]这提供了量子信息论和热力学之间的联系。
Rényi 熵也可以用作纠缠的度量。
5.4 量子纠缠度量
量子纠缠与量子系统失序现象、量子信息丧失程度密切相关。量子纠缠越大,则子系统越失序,量子信息丧失越多;反之,量子纠缠越小,子系统越有序,量子信息丧失越少。因此,冯诺伊曼熵可以用来定量地描述量子纠缠,另外,还有其它种度量也可以定量地描述量子纠缠。对于两体复合系统,这些纠缠度量较常遵守的几个规则为:
- 纠缠度量必须映射从密度算符至正实数。
- 假若整个复合系统不处于纠缠态,则纠缠度量必须为零。
- 对于纯态复合系统,纠缠度量必需约化为冯诺伊曼熵。
- 对于命定性的定域运算与经典通讯(local operation and classical communication)变换,纠缠度量不会增加。
对于两体纯态,只有冯诺伊曼熵能够量度量子纠缠,因为只有它能够满足某些量度量子纠缠必须遵守的判据。对于混合态,使用冯诺伊曼熵并不是能够量度量子纠缠的独有方法。
5.5 与不可分性
假设一个量子系统是由几个处于量子纠缠的子系统组成,而整体系统所具有的某种物理性质,子系统不能私自具有,这时,不能够对子系统给定这种物理性质,只能对整体系统给定这种物理性质,它具有 “不可分性”。不可分性不一定与空间有关,处于同一区域的几个物理系统,只要彼此之间没有任何纠缠,则它们各自可拥有自己的物理性质。物理学者艾雪·佩雷斯(Asher Peres)给出不可分性的数学定义式,可以计算出整体系统到底具有可分性还是不可分性。假设整体系统具有不可分性,并且这不可分性与空间无关,则可将它的几个子系统分离至两个相隔遥远的区域,这动作凸显出不可分性与定域性的不同──虽然几个子系统分别处于两个相隔遥远的区域,仍旧不可将它们个别处理。在 EPR 佯谬里,由于两个粒子分别处于两个相隔遥远的区域,整体系统被认为具有可分性,但因量子纠缠,整体系统实际具有不可分性,整体系统所具有明确的自旋 z 分量,两个粒子各自都不具有。
6. 应用
纠缠在量子信息中有许多应用。借助纠缠,一些原本不可能完成的任务可能会被实现。
纠缠的最著名的应用是超密集编码和量子隐形传态。[37]
大多数研究人员认为纠缠对于实现量子计算是必要的(尽管有些人对此有异议)。[38]
纠缠被用于量子密码的一些协议中。[39][40] 这是因为纠缠的 “共享噪声” 形成了一个极好的一次性密码本。此外,由于对纠缠对中任一成员的测量都会破坏它们之间共享的纠缠,基于纠缠的量子密码允许发送方和接收方更容易地检测到拦截器的存在。[来源请求]
在干涉测量中,纠缠对于超过标准量子极限和达到海森堡极限是必要的。[41]
6.1 纠缠态
有几种典型的纠缠态经常出现在理论和实验中。
对于两个量子位,贝尔态为 $$\left| \Phi^{\pm} \right\rangle = \frac{1}{\sqrt{2}} \left( \left| 0 \right\rangle_A \otimes \left| 0 \right\rangle_B \pm \left| 1 \right\rangle_A \otimes \left| 1 \right\rangle_B \right)~$$ $$\left| \Psi^{\pm} \right\rangle = \frac{1}{\sqrt{2}} \left( \left| 0 \right\rangle_A \otimes \left| 1 \right\rangle_B \pm \left| 1 \right\rangle_A \otimes \left| 0 \right\rangle_B \right)~$$
这四个纯态都是最大纠缠(根据纠缠熵),并形成两个量子位的希尔伯特空间的一个正交归一基(线性代数)。它们在贝尔定理中发挥着重要作用。
对于 $M>2$ 量子位,GHZ 态为
$$\left| GHZ \right\rangle = \frac{\left| 0 \right\rangle^{\otimes M} + \left| 1 \right\rangle^{\otimes M}}{\sqrt{2}}~,$$
当 $M=2$ 时,它退化为贝尔态 $\left| \Phi^{+} \right\rangle$。传统的 GHZ 态被定义为 $M=3$。GHZ 态偶尔会扩展到 qudits,即 $d$ 维而不是 2 维的系统。
此外,对于 $M>2$ 量子位,存在自旋压缩态。[42] 自旋压缩态是一类对自旋测量的不确定性满足一定限制的压缩相干态,并且必然是纠缠态。[43] 自旋压缩态是利用量子纠缠增强精确测量的良好候选者。[44]
对于两种玻色子模式,NOON 态为
最后,玻色子模式也存在双福克态,这可以通过将福克态馈送到通向分束器的两个臂中来得到。它们是 NOON 态的倍数之和,可以用来达到海森堡极限。[45]
对于适当选择的纠缠度量,贝尔态、GHZ 态和 NOON 态是最大纠缠,而自旋压缩态和双福克态只是部分纠缠。部分纠缠态通常更易于在实验中制备。
6.2 产生纠缠的方法
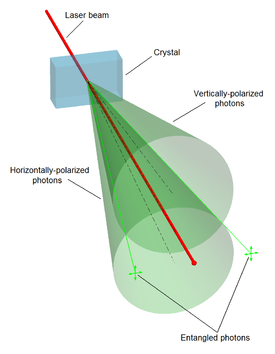
纠缠通常由亚原子粒子之间的直接相互作用产生。这些相互作用可以采取多种形式。最常用的方法之一是自发参量下转换,以产生一对偏振纠缠的光子。[27] 其他方法包括使用光纤耦合器来限制和混合光子、从量子点中双激子的衰变级联发射的光子、[46] 洪-欧-曼德尔效应的使用等等。在对贝尔定理最早的测试中,纠缠粒子是用原子级联产生的。
通过使用纠缠交换,也有可能在从不直接相互作用的量子系统之间产生纠缠。两个独立准备的全同粒子之间也可能存在纠缠,如果它们的波函数仅仅在空间上(至少部分)重叠。[47]
6.3 测试纠缠系统
密度矩阵 $\rho$ 如果可以被写成系综态的凸和,那么我们就说它是可分的,即 $$\rho = \sum_j p_j \rho_j^{(A)} \otimes \rho_j^{(B)}~$$ 其中概率满足 $1 \geq p_{j}\geq 0$。根据定义,如果一个态不是可分的,那么它就是纠缠态。
对于 2-Qubit 和 Qubit-Qutrit 系统(分别是 $2\times2$ 和 $2\times3$),简单的 Peres–Horodecki 判据为可分性提供了必要和充分判据,因此也在无意中提供了探测纠缠的必要和充分判据。
然而,对于一般情况,该判据仅仅是可分性的一个充分条件,因为当问题一般化时变得 NP 困难。[48][49] 其他可分性判据包括(但不仅限于)范围判据、缩减判据以及那些基于不确定性关系的判据。
Jon Magne Leinaas、Jan Myrheim 和 Eirik Ovrum 在他们的论文《纠缠的几何方面》中提出了一个数值方法。[50] Leinaas 等人提供了一种数值方法,迭代地向要测试的目标状态细化估计的可分状态,并检查目标状态是否确实可以达到。该算法的一个实现(包括内置的 Peres–Horodecki 判据测试)是 "StateSeparator" web 应用程序。
2016 年,中国发射了世界上第一颗量子通信卫星。[51] 价值 1 亿美元的量子科学实验卫星任务于 2016 年 8 月 16 日当地时间 01:40 在中国北部的酒泉卫星发射中心启动。
在接下来的两年里,这颗以中国古代哲学家墨子的名字命名的卫星将展示地球和空间之间的量子通信的可行性,并在前所未有的距离上测试量子纠缠。
2017 年 6 月 16 日,在《科学》杂志上,Yin 等人报告了他们创造的 1,203 千米量子纠缠距离新记录,他们的实验在严格的爱因斯坦局域性条件下,从 “墨子号” 卫星到位于云南丽江和青海德令哈的基地,证明了双光子对的存在和贝尔不等式的违反,达到了 2.37±0.09 的 CHSH 估值,其传输效率比先前的光纤实验提高了一个数量级。[52][53]
6.4 量子纠缠在能量回收领域的应用
美国亚利桑那大学的研究人员借助量子力学中的量子干 涉原理研制了一种新型材料,该材料能够有效地将热能转化 为电能。该材料的特点是非常薄,其厚度只有百万分之一英 尺,应用比较方便,所需空间较小。主持该项任务的研究团 队表示,如果用这种极其薄的新型功能材料将汽车的整个排 气系统全部包裹起来,利用排气系统转化得到的电能将足以 点亮 200 支 100W 的灯泡。根据此实验,我们有理由憧憬,未来能够将损失的热能有效利用,从而大幅度减少能量的损 失,提升能量转换利用率。如果将热能转化为其他形式的能 量,能够提升各类用电设备的工作时间和稳定性,大幅降低在电源如何有效储能这一方面的研究投入。同时如若减小能 量损耗,可以有效降低资源的开发使用率,减小对环境的污 染和对地球的过度开发,为可持续发展提供基础条件,为人 类文明在地球上的延续提供环境保证。
6.5 量子纠缠在信息加密领域的应用
信息的加密与解密在军事、商业等各方面自古以来都是 一组相互促进、共同发展的共生技术。该技术的发展离不开 当时科技条件的支持,同时也是当时科技条件的一种反应。但是无论加密方式多复杂,只要知道其中基本的规律,通过 反规律而行之一般仍然能够破解加密信息。然而通过在信息 传播过程中进行 “量子加密”,就能够将信息保护视为 “绝 对安全” 的级别。之所以安全,是因为假如有人闯入信号传 输的网络,光子束会发生严重紊乱,导致信号传输网络中的 每一个信号节点的探测器增加错误等级,相当于发出了受到 袭击的警告信息,这时发送端和接收端双方都会随机选择若 干键值的子集进行匹配,只有全部匹配才认为没有窃听,倘 若有一点不匹配则认为信号被窃听。实际上,只要有闯入者 进行尝试解码,这一举动便会导致量子密码系统改变自身的 状态。因此只要发生窃听行为,都会被检查者发现,从而终 止机密信息的传输或更换新密钥,进而保护各类机密信息。
6.6 量子纠缠在通信领域的应用
当前的各类通信主要是通过电磁波或光纤的方式进行传 输,由于传输距离基本未超出过太阳系,所以通信速度能够 基本实现全球 “同步” 直播。但确切地来讲,任何类型的资 料通过当前的信息传输介质传播,都需要一些时间才能到达 最终的接收方,只是用时较短导致人类的感官难以察觉分辨 而已,距离真正的 “即时通信” 还存在技术手段上的硬伤。然而,量子纠缠现象为即时通信提供了可能性。也保持着特 别的关联性,对一个粒子的操作会影响到另一个粒子。简单 来说就是,处于纠缠态的两个粒子,即使距离再遥远,当其 中一个粒子被测量或者被观测到时它的状态会被确定,而此 时与之纠缠的另一个粒子的状态也会随之发生即时的改变。因此,利用这一现象,我们可以通过操纵其中一个粒子的方 式引起相互存在纠缠关系的其他粒子的状态发生 “即时” 变 化,从而完成在距离任意遥远的两点之间的信息传送。例如,随着未来人类可利用宇宙空间的不断延伸,可能会出现人类 之间或人类与其他物种之间横跨星系的交流,这种交流如果 通过传统的通信方式进行,可能会导致延时数小时甚至数年。但是通过量子纠缠进行量子通信,则能够解决星际或宇宙之 间任意距离的实时通信问题。当然,这一应用也面临着巨大 的技术难题,目前还处于方案设想及初级试验阶段。
6.7 量子纠缠在计算领域的应用
量子计算与传统的计算机相比,其计算速度要快得多,基本上是指数倍的关系。大致原理为,计算机内部采用 $0$ 和 $1$ 二进制,计算采取二进制的加减乘除算法,之所以比人计 算得快,只是因为计算机内部的位数较多,以及机器计算速 度比人要快得多,但是其计算时还是采用特别笨的办法,一 步一步按照先后顺序来算,只是速度快了而已。而量子计算 不同,量子的 $0$ 和 $1$ 是不确定的,可以同时认为是 $0$ 也可以 认为是 $1$,也就是说,量子计算是并行运算,没有按照先后 顺序一步一步算,而是同时计算很多步。以 “走迷宫” 为例,对于复杂的迷宫,当前的计算机需要从一个点出发,遇到十 字路,只能走一个方向,然后发现走不通,再返回到这个十 字路口去走向另一个方向,这样不断 “试错”,最终找到一 条正确的路径,因此需要一定的时间;而量子计算不同,量 子可以同时从一个点出发,遇到一个十字路口,同时向四个 方向前进,再遇到另一个十字路口,还是同时向四个方向前 进,因此其不是逐个试错,而是同时试错,所以速度比传统 计算机呈指数级别增加。“人工智能” 作为当前科技领域的 发展热点,其核心内容在于算法,通过大量的数据进行对比 学习等方式,进行分类和特征提取。但是由于当前的计算资 源和计算速度有限,导致计算速度不够或计算容量不够,使 得 “人工智能” 在某些复杂的场合和某些对瞬时性要求较高 的时候变成了 “人工智障”。如果届时有量子计算机问世,同时开发相配套的量子算法,将会使得机械学习训练的时间 大幅缩短,人工智能的应用场景也将会更加丰富,在智慧城 市、大数据分析和金融模型开发等方面都将大有可为。
6.8 量子纠缠在军事领域的应用
在军事领域,如有效利用量子纠缠原理,或许会制造出 具备颠覆性打击功能的量子武器。根据研究表明,在量子物 理学攻关、试验成功后,至少可生产如下武器:一是重力波 炮。由于在宇宙中缺乏媒介,声波或冲击波等波无法在没有 介质的情况下传播,因此,传统的爆炸性武器(甚至包括核 武器)在缺乏媒介的情况下,毁伤效果将变差。而重力波则 不受这个限制,重力波的传播不受传播介质数量多少的限制,因此在宇宙中仍然有很强的毁伤效果;二是反物质武器。根 据量子力学推论,宇宙中存在由反粒子组成的反物质,当 “正 物质” 与 “反物质” 相遇时,就会发生湮灭效应,释放出巨 大的能量。科学家设想根据此效应制造反物质武器,如成功 问世,毁伤效能将远胜于当前的氢弹和原子弹;三是人造重 力场,其实就是一个人造黑洞,任何物质只要碰上重力场发 生器,其自身就会立即被撕碎,瞬间化为乌有。此外还有能 够抵抗几乎所有物理攻击的防护性武器——量子防护罩[54]。
7. 参考文献
[1] ^Einstein A, Podolsky B, Rosen N; Podolsky; Rosen (1935). "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?" (PDF). Phys. Rev. 47 (10): 777–780. Bibcode:1935PhRv...47..777E. doi:10.1103/PhysRev.47.777.CS1 maint: Multiple names: authors list (link).
[2] ^Alisa Bokulich, Gregg Jaeger, Philosophy of Quantum Information and Entanglement, Cambridge University Press, 2010, xv..
[3] ^Letter from Einstein to Max Born, 3 March 1947; The Born-Einstein Letters; Correspondence between Albert Einstein and Max and Hedwig Born from 1916 to 1955, Walker, New York, 1971. (cited in M. P. Hobson; et al., Quantum Entanglement and Communication Complexity (1998), pp. 1/13, CiteSeerX 10.1.1.20.8324).
[4] ^Freedman, Stuart J.; Clauser, John F. (1972). "Experimental Test of Local Hidden-Variable Theories". Physical Review Letters. 28 (14): 938–941. Bibcode:1972PhRvL..28..938F. doi:10.1103/PhysRevLett.28.938..
[5] ^Asher Peres, Quantum Theory, Concepts and Methods, Kluwer, 1993; ISBN 0-7923-2549-4 p. 115..
[6] ^Rupert W., Anderson (28 March 2015). The Cosmic Compendium: Interstellar Travel (First ed.). The Cosmic Compendium. p. 100. ISBN 9781329022027..
[7] ^magazine, Elizabeth Gibney, Nature. "Cosmic Test Bolsters Einstein's "Spooky Action at a Distance"". Scientific American (in 英语). Retrieved 2017-02-04..
[8] ^I. Gerhardt; Q. Liu; A. Lamas-Linares; J. Skaar; V. Scarani; V. Makarov; C. Kurtsiefer (2011), "Experimentally faking the violation of Bell's inequalities", Phys. Rev. Lett., 107 (17): 170404, arXiv:1106.3224, Bibcode:2011PhRvL.107q0404G, doi:10.1103/PhysRevLett.107.170404, PMID 22107491.
[9] ^Santos, E (2004). "The failure to perform a loophole-free test of Bell's Inequality supports local realism". Foundations of Physics. 34 (11): 1643–1673. Bibcode:2004FoPh...34.1643S. doi:10.1007/s10701-004-1308-z..
[10] ^H. Zbinden; et al. (2001). "Experimental test of nonlocal quantum correlations in relativistic configurations". Phys. Rev. A. 63 (2): 22111. arXiv:quant-ph/0007009. Bibcode:2001PhRvA..63b2111Z. doi:10.1103/PhysRevA.63.022111..
[11] ^Some of the history of both referenced Zbinden, et al. experiments is provided in Gilder, L., The Age of Entanglement, Vintage Books, 2008, pp. 321–324..
[12] ^Cirel'son, B. S. (1980). "Quantum generalizations of Bell's inequality". Letters in Mathematical Physics. 4 (2): 93–100. Bibcode:1980LMaPh...4...93C. doi:10.1007/BF00417500..
[13] ^Moreva, Ekaterina (2014). "Time from quantum entanglement: an experimental illustration". Physical Review A. 89 (5): 052122. arXiv:1310.4691. Bibcode:2014PhRvA..89e2122M. doi:10.1103/PhysRevA.89.052122..
[14] ^"Entangled toy universe shows time may be an illusion". Retrieved 13 October 2014..
[15] ^David Deutsch, The Beginning of infinity. Page 299.
[16] ^"Quantum Experiment Shows How Time 'Emerges' from Entanglement". Medium. 2013-10-23. Retrieved 13 October 2014..
[17] ^"New Quantum Theory Could Explain the Flow of Time". Wired. 2014-04-25. Retrieved 13 October 2014..
[18] ^Van Raamsdonk, Mark (2010-06-19). "Building up spacetime with quantum entanglement". General Relativity and Gravitation (in 英语). 42 (10): 2323–2329. arXiv:1005.3035. doi:10.1007/s10714-010-1034-0. ISSN 0001-7701..
[19] ^Lee, Jae-Weon; Kim, Hyeong-Chan; Lee, Jungjai (2013). "Gravity from quantum information". Journal of the Korean Physical Society (in 英语). 63 (5): 1094–1098. arXiv:1001.5445. doi:10.3938/jkps.63.1094. ISSN 0374-4884..
[20] ^Swingle, Brian; Van Raamsdonk, Mark (2014-05-12). "Universality of Gravity from Entanglement". arXiv:1405.2933 [hep-th]..
[21] ^周正威, 郭光灿. 量子信息讲座续讲 第三讲 量子纠缠态[J]. 物理, 2000, 29(11): 0-0..
[22] ^Nicolas Brunner; Daniel Cavalcanti; Stefano Pironio; Valerio Scarani; Stephanie Wehner (2014). "Bell nonlocality". Rev. Mod. Phys. 86 (2): 419–478. arXiv:1303.2849. doi:10.1103/RevModPhys.86.419..
[23] ^Werner, R.F. (1989). "Quantum States with Einstein-Podolsky-Rosen correlations admitting a hidden-variable model". Physical Review A. 40 (8): 4277–4281. Bibcode:1989PhRvA..40.4277W. doi:10.1103/PhysRevA.40.4277. PMID 9902666..
[24] ^R. Augusiak, M. Demianowicz, J. Tura and A. Acín (2015). "Entanglement and Nonlocality are Inequivalent for Any Number of Parties". Phys. Rev. Lett. 115 (3): 030404. arXiv:1407.3114. doi:10.1103/PhysRevLett.115.030404. hdl:2117/78836. PMID 26230773.CS1 maint: Multiple names: authors list (link).
[25] ^Tamas Vértesi, Nicolas Brunner (2014). "Disproving the Peres conjecture: Bell nonlocality from bipartite bound entanglement". Nature Communications. 5 (5297): 5297. arXiv:1405.4502. doi:10.1038/ncomms6297. PMID 25370352.CS1 maint: Uses authors parameter (link).
[26] ^In the literature "non-locality" is sometimes used to characterize concepts that differ from the non-existence of a local hidden variable model, e.g., whether states can be distinguished by local measurements and which can occur also for non-entangled states (see, e.g., Charles H. Bennett, David P. DiVincenzo, Christopher A. Fuchs, Tal Mor, Eric Rains, Peter W. Shor, John A. Smolin, and William K. Wootters (1999). "Quantum nonlocality without entanglement". Phys. Rev. A. 59 (2): 1070–1091. arXiv:quant-ph/9804053. doi:10.1103/PhysRevA.59.1070.CS1 maint: Uses authors parameter (link)). This non-standard use of the term is not discussed here..
[27] ^Horodecki R, Horodecki P, Horodecki M, Horodecki K; Horodecki; Horodecki; Horodecki (2009). "Quantum entanglement". Rev. Mod. Phys. 81 (2): 865–942. arXiv:quant-ph/0702225. Bibcode:2009RvMP...81..865H. doi:10.1103/RevModPhys.81.865.CS1 maint: Multiple names: authors list (link).
[28] ^>Grassl, M.; Rötteler, M.; Beth, T. (1998). "Computing local invariants of quantum-bit systems". Phys. Rev. A. 58 (3): 1833–1839. arXiv:quant-ph/9712040. doi:10.1103/PhysRevA.58.1833..
[29] ^B. Kraus (2010). "Local unitary equivalence of multipartite pure states". Phys. Rev. Lett. 104 (2): 020504. arXiv:0909.5152. doi:10.1103/PhysRevLett.104.020504. PMID 20366579..
[30] ^M. A. Nielsen (1999). "Conditions for a Class of Entanglement Transformations". Phys. Rev. Lett. 83 (2): 436. arXiv:quant-ph/9811053. doi:10.1103/PhysRevLett.83.436..
[31] ^Gour, G. & Wallach, N. R. (2013). "Classification of Multipartite Entanglement of All Finite Dimensionality". Phys. Rev. Lett. 111 (6): 060502. arXiv:1304.7259. doi:10.1103/PhysRevLett.111.060502. PMID 23971544.CS1 maint: Uses authors parameter (link).
[32] ^Horodecki, M.; Horodecki, P.; Horodecki, R. (1998). "Mixed-state entanglement and distillation: Is there a bound entanglement in nature?". Phys. Rev. Lett. 80 (1998): 5239–5242. arXiv:quant-ph/9801069. doi:10.1103/PhysRevLett.80.5239..
[33] ^H. M. Wiseman, S. J. Jones, and A. C. Doherty (2007). "Steering, Entanglement, Nonlocality, and the Einstein-Podolsky-Rosen Paradox". Phys. Rev. Lett. 98 (14): 140402. arXiv:quant-ph/0612147. doi:10.1103/PhysRevLett.98.140402. PMID 17501251.CS1 maint: Uses authors parameter (link).
[34] ^Cerf, Nicolas J.; Cleve, Richard. "Information-theoretic interpretation of quantum error-correcting codes" (PDF)..
[35] ^Plenio; Virmani (2007). "An introduction to entanglement measures". Quant. Inf. Comp. 1: 1–51. arXiv:quant-ph/0504163. Bibcode:2005quant.ph..4163P..
[36] ^Wolchover, Natalie (25 April 2014). "New Quantum Theory Could Explain the Flow of Time". www.wired.com. Quanta Magazine. Retrieved 27 April 2014..
[37] ^Bouwmeester, Dik; Pan, Jian-Wei; Mattle, Klaus; Eibl, Manfred; Weinfurter, Harald & Zeilinger, Anton (1997). "Experimental Quantum Teleportation" (PDF). Nature. 390 (6660): 575–579. Bibcode:1997Natur.390..575B. doi:10.1038/37539..
[38] ^Richard Jozsa; Noah Linden (2002). "On the role of entanglement in quantum computational speed-up". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 459 (2036): 2011–2032. arXiv:quant-ph/0201143. Bibcode:2003RSPSA.459.2011J. CiteSeerX 10.1.1.251.7637. doi:10.1098/rspa.2002.1097..
[39] ^Ekert, Artur K. (1991). "Quantum cryptography based on Bell's theorem". Physical Review Letters. 67 (6): 661–663. Bibcode:1991PhRvL..67..661E. doi:10.1103/PhysRevLett.67.661. PMID 10044956..
[40] ^Yin, Juan; Cao, Yuan; Yong, Hai-Lin; Ren, Ji-Gang; Liang, Hao; Liao, Sheng-Kai; Zhou, Fei; Liu, Chang; Wu, Yu-Ping; Pan, Ge-Sheng; Zhang, Qiang; Peng, Cheng-Zhi; Pan, Jian-Wei (2010). "Contextuality offers device-independent security". arXiv:1006.0468 [quant-ph]..
[41] ^Pezze, Luca & Smerzi, Augusto (2009). "Entanglement, Nonlinear Dynamics, and the Heisenberg Limit". Phys. Rev. Lett. 102 (10): 100401. arXiv:0711.4840. Bibcode:2009PhRvL.102j0401P. doi:10.1103/PhysRevLett.102.100401. PMID 19392092..
[42] ^Database error – Qwiki Archived 21 8 月 2012 at the Wayback Machine.
[43] ^Kitagawa, Masahiro; Ueda, Masahito (1993). "Squeezed Spin States". Phys. Rev. A. 47 (6): 5138–5143. Bibcode:1993PhRvA..47.5138K. doi:10.1103/physreva.47.5138. PMID 9909547..
[44] ^Wineland, D. J.; Bollinger, J. J.; Itano, W. M.; Moore, F. L.; Heinzen, D. J. (1992). "Spin squeezing and reduced quantum noise in spectroscopy". Phys. Rev. A. 46 (11): R6797–R6800. Bibcode:1992PhRvA..46.6797W. doi:10.1103/PhysRevA.46.R6797. PMID 9908086..
[45] ^Holland, M. J; Burnett, K (1993). "Interferometric detection of optical phase shifts at the Heisenberg limit". Physical Review Letters. 71 (9): 1355–1358. doi:10.1103/PhysRevLett.71.1355. PMID 10055519..
[46] ^Akopian, N. (2006). "Entangled Photon Pairs from Semiconductor Quantum Dots". Phys. Rev. Lett. 96 (2): 130501. arXiv:quant-ph/0509060. Bibcode:2006PhRvL..96b0501D. doi:10.1103/PhysRevLett.96.020501. PMID 16486553..
[47] ^Rosario Lo Franco and Giuseppe Compagno, "Indistinguishability of Elementary Systems as a Resource for Quantum Information Processing", Phys. Rev. Lett. 120, 240403, 14 June 2018..
[48] ^Gurvits, L., Classical deterministic complexity of Edmonds' problem and quantum entanglement, in Proceedings of the 35th ACM Symposium on Theory of Computing, ACM Press, New York, 2003..
[49] ^Sevag Gharibian, Strong NP-Hardness of the Quantum Separability Problem, Quantum Information and what's known as Quantum Computing, Vol. 10, No. 3&4, pp. 343–360, 2010. arXiv:0810.4507..
[50] ^"Geometrical aspects of entanglement", Physical Review A 74, 012313 (2006).
[51] ^https://web.archive.org/web/20221109185623/http://physicsworld.com/cws/article/news/2016/aug/16/china-launches-world-s-first-quantum-science-satellite.
[52] ^Science 16 Jun 2017: Vol. 356, Issue 6343, pp. 1140-1144 DOI: 10.1126/science.aan3211.
[53] ^"China's quantum satellite achieves 'spooky action' at record distance". 2017-06-14..
[54] ^张皓泊 . 量子通信与量子计算 [J]. 中国新技术新产品,2018(20):78-79..