量子不和谐

贡献者：待更新

　　（本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

　　在量子信息论中, 量子不和谐 是对一个量子系统中的两个子系统之间非经典相关性的度量。它包括了由于量子物理学效应而产生的关联性，但不一定涉及量子纠缠。

　　量子不和谐的概念是由 Hardord OLLivier，Wojciech H. Zurek[1][2] 亨德森和 Vlatko Vedral 各自提出的。[3] 奥利维尔（OLLivier）和祖里克（Zurek）也将其作为定量相关性的量化指标。[2] 从这两个研究小组的工作中可以看出，量子关联可以以某种混合可分离状态下存在；[4] 换句话说，单独的可分离性并不意味着没有量子关联。因此，量子不和谐的概念超越了早先在纠缠态和可分离(非纠缠)量子态之间所做的区分。

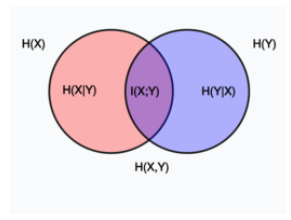
1. 定义和数学关系

图 1：单个 H（X），H（Y），相关的 H（X，Y）及具有互信息 I（X，Y）的一对相关子系统 X，Y 的条件熵

　　在数学术语中，量子不和谐是由量子互信息定义的。更具体地说，量子不和谐是两个表达式之间的差异，在经典极限中，每个表达式都表达交互信息。这两个表达式是：

\begin{equation} \begin{aligned} I(A; B) &= H(A) + H(B) - H(A, B) \\ J(A; B) &= H(A) - H(A \mid B) \\ J(A; B) &= H(A) - H(A \mid B) \end{aligned}~ \end{equation}

在经典案例中，$H(A)$ 是信息熵，$H(A, B)$ 为相关熵和 $H(A|B)$ 为条件熵，这两个表达式产生相同的结果。在非经典情况下，使用量子物理类比的三项 $S(\rho_A)$ the 冯·诺依曼熵，$S(\rho)$ the 组合量子熵和 $S(\rho_A|\rho_B)$ 条件熵的量子概括（不要混淆条件量子熵），各自为概率密度函数 $\rho$： $$I(\rho) = S(\rho_A) + S(\rho_B) - S(\rho)~$$ $$J_A(\rho) = S(\rho_B) - S(\rho_B|\rho_A)~$$ 这两种表达方式的区别 $I(\rho) - J_A(\rho)$ 证实了依赖于基础的量子不和谐，这在某种意义上是不对称的 $D_A(\rho)$ 可以不同于 $D_B(\rho)$。符号 $J$ 代表可归因于经典相关性的部分相对熵，并根据所选特征基的不而不同变化。因此，为了让量子不和谐独立于基本反映纯粹的经典关联，有必要首先在特征基上所有可能映射测量的集合中最大化： $$\mathcal{D}_A(\rho) = I(\rho) - \max_{\{\Pi_j^A\}} J_{\{\Pi_j^A\}} (\rho) = S(\rho_A) - S(\rho) + \min_{\{\Pi_j^A\}} S(\rho_B|\{\Pi_j^A\})~$$ 非零量子不和谐表示由于量子算子的非交换性的非交换性而存在的相关性。[8] 对于纯净状态，量子不和谐成为衡量量子纠缠的度量,[9] 更确切地说，在这种情况下，它等于纠缠熵。[4]

　　消失的量子不和谐是指针状态的一个判断标准，它们构成了一个系统的优选的有效经典状态。[2] 可以证明，量子不和谐必须是非负的，量子不和谐消失的状态实际上可以用指针状态来识别。[10] 其他条件也已确定，可以类似于佩雷斯-霍洛德茨基（Peres—Holodecki）标准[11]，并与冯·诺依曼熵的强次可加性有关。[12]

　　科学家们已经努力将量子不和谐的定义扩展到连续变量系统，[13] 特别是高斯态描述的二分系统。[4][14] 最新的研究[15] 证明了高斯不和谐的上限[4][14] 确实与高斯态的量子不和谐一致，当后者属于一个合适的高斯态大家族时。

　　计算量子不和谐是 NP 完全的，因此在一般情况下很难计算。[16]

2. 性能

　　祖雷克（Zurek）对不和谐提供了一种物理解释，表明它 “决定了量子效率和经麦克斯韦（Maxwell＇s）守护程序之间的差异...在从相关量子系统的集合中提取的工作中”。< ref name="zurek-2003">W. H. Zurek: 量子不和谐和麦克斯韦的恶魔”，物理评论，卷。67，012320 (2003)，abstract</ref >

　　从操作的角度来看，不和谐也可以看着是一种 “扩展量子态合并协议中的纠缠消耗”。[12][17] 为非纠缠量子关联提供证据通常涉及到精细的量子断层摄影方法；然而，在 2011 年，这种相关性可以在室温条件下，通过使用氯仿代表二个量子位的量子系统的氯仿分子，在核磁共振实验中得到证明。[18][19]

　　量子不和谐被认为是以某种性能基础，这种性能归因于某些混合状态量子系统的量子计算，[20] 用一个混合量子态代表一个统计系综纯净状态(见量子统计力学)。量子不和谐可以成为量子处理器的资源的观点在 2012 年得到了进一步巩固，在那里，实验证明，二分系统之间的不和谐可以被用来编码只能通过相干量子交互访问的信息。[21] 量子不和谐是复合量子系统中一个子系统最小相干性指标，因此，它在相位估计的干涉方案中扮演重要的资源作用。[22][23] 最新的研究表明：[24] 将量子不和谐量子密码术的一种资源，能够在完全没有纠缠的情况下保证量子密钥分发的安全性。

　　量子不和谐在某些方面不同于量子纠缠，量子不和谐比量子纠缠更能适应耗散环境。基于对不和谐和并发的不和谐的动态比较，已经证明了这一点，无论在马尔可夫环境和非马尔可夫环境中都是如此，而不和谐被证明更加强烈。[25] 这已经表明，至少对于某些处于热平衡的量子位对模型，以及形成一个与热浴槽有关的开放量子系统，在一定的温度范围内，量子不和谐随着温度的升高而增加，因此显示的行为与纠缠相比有相当的差异。此外，令人惊讶的是，经典相关性实际上随着量子不和谐的增加而降低。[26] 非零量子不和谐甚至会持续到子系统之一承受无限加速的极限，而在这种情况下，由于 Unruh 效应，量子纠缠下降到零。[27]

3. 替代措施

　　就局部纯态的蒸馏而言，一个可操作的度量是 “量子缺陷”。[28] 单向和零向版本被证明等于量子的相对熵。[29]

　　非经典相关的其他度量包括测量诱导扰动（MID）度量、局部无效单一的(LNU)距离[30] 和各种基于熵的度量。[31]

　　基于希尔伯特-施密特（Hilbert-Schmidt）距离，存在一个不和谐的几何指标，[5] 它遵循因式分解定律，[32] 可以和冯·诺依曼的测量结果联系起来，[33] 但总的来说并不是一个可靠的衡量标准。

　　不和谐型关联的可靠的、可计算的和可操作的度量是局部量子不确定性[22] 和干涉能力。[23]

4. 参考文献

　　 [1] ^Wojciech H. Zurek, Einselection and decoherence from an information theory perspective, Annalen der Physik vol. 9, 855–864 (2000) abstract.

　　 [2] ^Harold Ollivier and Wojciech H. Zurek, Quantum Discord: A Measure of the Quantumness of Correlations, Physical Review Letters vol. 88, 017901 (2001) abstract.

　　 [3] ^L. Henderson and V. Vedral: Classical, quantum and total correlations, Journal of Physics A 34, 6899 (2001), doi:10.1088/0305-4470/34/35/315 [1].

　　 [4] ^Paolo Giorda, Matteo G. A. Paris: Gaussian quantum discord, quant-ph arXiv:1003.3207v2 (submitted on 16 Mar 2010, version of 22 March 2010) p. 1.

　　 [5] ^Borivoje Dakić, Vlatko Vedral, Caslav Brukner: Necessary and sufficient condition for nonzero quantum discord, Phys. Rev. Lett., vol. 105, nr. 19, 190502 (2010), arXiv:1004.0190v2 (submitted 1 April 2010, version of 3 November 2010).

　　 [6] ^For a succinct overview see for ex arXiv:0809.1723v2.

　　 [7] ^For a more detailed overview see for ex. Signatures of nonclassicality in mixed-state quantum computation, Physical Review A vol. 79, 042325 (2009), doi:10.1103/PhysRevA.79.042325 arXiv:0811.4003[永久失效连结] and see for ex. Wojciech H. Zurek: Decoherence and the transition from quantum to classical - revisited, p. 11.

　　 [8] ^Shunlong Luo: Quantum discord for two-qubit systems, Physical Review A, vol. 77, 042303 (2008) abstract[永久失效连结].

　　 [9] ^Animesh Datta, Anil Shaji, Carlton M. Caves: Quantum discord and the power of one qubit, arXiv:0709.0548v1 [quant-ph], 4 Sep 2007, p. 4.

　　 [10] ^Animesh Datta: A condition for the nullity of quantum discord, arXiv:1003.5256v2.

　　 [11] ^Bogna Bylicka, Dariusz Chru´sci´nski: Witnessing quantum discord in 2 x N systems, arXiv:1004.0434v1 [quant-ph], 3 April 2010.

　　 [12] ^Vaibhav Madhok, Animesh Datta: Role of quantum discord in quantum communication arXiv:1107.0994v1, (submitted 5 July 2011).

　　 [13] ^C. Weedbrook, S. Pirandola, R. Garcia-Patron, N. J. Cerf, T. C. Ralph, J. H. Shapiro, S. Lloyd: Gaussian Quantum Information, Reviews of Modern Physics 84, 621 (2012), available from arXiv:1110.3234v1 [2].

　　 [14] ^Gerardo Adesso, Animesh Datta: Quantum versus classical correlations in Gaussian states, Phys. Rev. Lett. 105, 030501 (2010), available from arXiv:1003.4979v2 [quant-ph], 15 July 2010.

　　 [15] ^S. Pirandola, G. Spedalieri, S. L. Braunstein, N. J. Cerf, S. Lloyd: Optimality of Gaussian Discord, Phys. Rev. Lett. 113, 140405 (2014), available from arXiv:1309.2215v3 [3], 26 Nov 2014.

　　 [16] ^Huang, Yichen (21 March 2014). "Computing quantum discord is NP-complete". New Journal of Physics. 16 (3): 033027. arXiv:1305.5941. Bibcode:2014NJPh...16c3027H. doi:10.1088/1367-2630/16/3/033027..

　　 [17] ^D. Cavalcanti, L. Aolita, S. Boixo, K. Modi, M. Piani, A. Winter: Operational interpretations of quantum discord, quant-ph, arXiv:1008.3205.

　　 [18] ^R. Auccaise, J. Maziero, L. C. Céleri, D. O. Soares-Pinto, E. R. deAzevedo, T. J. Bonagamba, R. S. Sarthour, I. S. Oliveira, R. M. Serra: Experimentally Witnessing the Quantumness of Correlations, Physical Review Letters, vol. 107, 070501 (2011) abstract (arXiv:1104.1596).

　　 [19] ^Miranda Marquit: Quantum correlations – without entanglement, PhysOrg, August 24, 2011.

　　 [20] ^Animesh Datta, Anil Shaji, Carlton M. Caves: Quantum discord and the power of one qubit, arXiv:0709.0548v1 [quant-ph], 4 Sep 2007, p. 1.

　　 [21] ^M. Gu, H. Chrzanowski, S. Assad, T. Symul, K. Modi, T. C.Ralph, V.Vedral, P.K. Lam. "Observing the operational significance of discord consumption", Nature Physics 8, 671–675, 2012, [4]'.

　　 [22] ^D. Girolami, T. Tufarelli, and G. Adesso, Characterizing Nonclassical Correlations via Local Quantum Uncertainty, Phys. Rev. Lett. 110, 240402 (2013) [5].

　　 [23] ^D. Girolami et al., Quantum Discord Determines the Interferometric Power of Quantum States, Phys. Rev. Lett. 112, 210401 (2014) [6].

　　 [24] ^S. Pirandola: Quantum discord as a resource for quantum cryptography, Sci. Rep. 4, 6956 (2014), available from [7].

　　 [25] ^See [8] as well as [9] and citations therein.

　　 [26] ^T. Werlang, G. Rigolin: Thermal and magnetic discord in Heisenberg models, Physical Review A, vol. 81, no. 4 (044101) (2010), doi:10.1103/PhysRevA.81.044101 abstract, fulltext (arXiv).

　　 [27] ^Animesh Datta: Quantum discord between relatively accelerated observers, arXiv:0905.3301v1 [quant-ph] 20 May 2009, [10].

　　 [28] ^Jonathan Oppenheim, Michał Horodecki, Paweł Horodecki and Ryszard Horodecki:"Thermodynamical Approach to Quantifying Quantum Correlations" Physical Review Letters 89, 180402 (2002) [11].

　　 [29] ^Michał Horodecki, Paweł Horodecki, Ryszard Horodecki, Jonathan Oppenheim, Aditi Sen De, Ujjwal Sen, Barbara Synak-Radtke: "Local versus nonlocal information in quantum-information theory: Formalism and phenomena" Physical Review A 71, 062307 (2005) [12].

　　 [30] ^see for ex.: Animesh Datta, Sevag Gharibian: Signatures of non-classicality in mixed-state quantum computation, Physical Review A vol. 79, 042325 (2009) abstract, arXiv:0811.4003[永久失效连结].

　　 [31] ^Matthias Lang, Anil Shaji, Carlton Caves: Entropic measures of nonclassical correlations, American Physical Society, APS March Meeting 2011, March 21–25, 2011, abstract #X29.007, arXiv:1105.4920.

　　 [32] ^Wei Song, Long-Bao Yu, Ping Dong, Da-Chuang Li, Ming Yang, Zhuo-Liang Cao: Geometric measure of quantum discord and the geometry of a class of two-qubit states, arXiv:1112.4318v2 (submitted on 19 December 2011, version of 21 December 2011).

　　 [33] ^S. Lu, S. Fu: Geometric measure of quantum discord, Phys. Rev. A, vol. 82, no. 3, 034302 (2010).