经典物理学
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译)
经典物理学是指早于近代物理、更完整或被更广泛应用的物理学理论。如果一个目前被接受的理论被认为是近代的,并且它的提出代表了一个主要的范式转变,那么以前的理论,或者基于旧范式的新理论,通常就被称为属于 “经典物理学” 的领域。
因此,经典理论的定义取决于语境。当近代物理理论在特定情况出现不必要的复杂时,通常会用到经典物理的概念。通常经典物理学是指 1900 年前的物理学,而近代物理学是指 1900 年后包含量子力学和相对论的物理学。[1]
1. 概述
经典理论在物理学中至少有两种不同的含义。在量子力学的背景下,经典理论是指不使用量子化规范的物理理论,包括经典力学和相对论。[2]同样,经典场论,如广义相对论和经典电磁学,它们都不使用量子力学的理论。[3]在广义相对论和狭义相对论的背景下,经典理论是那些服从伽利略相对性的理论。[4]
根据不同的观点,经典物理学中包含的理论分支有以下几种:
- 经典力学
- 牛顿运动定律
- 经典拉格朗日和哈密顿公式
- 经典电动力学(麦克斯韦方程)
- 经典热力学
- 狭义相对论和广义相对论
- 经典混沌理论和非线性动力学
2. 与近代物理学的比较
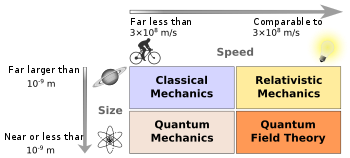
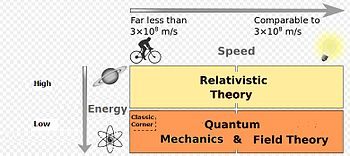
与经典物理学相反,“近代物理学” 是一个稍微宽松的术语,它可能仅指量子物理学或一般的 20 世纪和 21 世纪物理学。当条件适用时,近代物理学包括量子理论和相对论。
当一个物理系统满足经典物理定律近似有效的条件时,它可以用经典物理来描述。实际上,从比原子和分子大的物体到宏观和天文领域的物体,都可以用经典力学很好地描述(理解)。从原子层次和更低层次开始,经典物理定律就被打破,通常不能对自然作出正确描述。在尺寸和场强足够大以至于可忽略量子力学效应的情况下,电磁场和力可以用经典电动力学很好地描述。与量子物理不同,尽管量子力学的确存在确定性的解释,但经典物理的基本特征就是完全确定的理论。
从经典物理学作为非相对论物理学的观点来看,广义相对论和狭义相对论的假设与经典理论有很大不同,特别是在时间流逝、空间几何、自由落体运动和光的传播方面。过去,假设光通过静止的介质(以太)传播,光与经典力学相符合,但后来以太被证明是不存在的。
数学上,经典物理方程是普朗克常数不出现的方程。根据对应原理和埃伦费斯特定理,当一个系统变得更大或更大时,经典动力学更加适用,除了一些例外,如超流体。这就是为什么我们在处理日常物体时通常可以忽略量子力学,经典描述就足够了。然而,物理学中最活跃的研究领域之一是经典量子通信。这一研究领域是关于量子物理定律如何在经典物理的大尺度限制下产生经典物理的发现。
3. 计算机建模和人工计算,近代与经典的比较
今天,一台计算机在几秒钟内完成数百万次算术运算来求解一个经典微分方程,而牛顿(微积分之父之一) 即使是这个特定方程的发现者,也需要几个小时才能通过人工计算来求解同一方程。
计算机建模对量子和相对论物理至关重要,经典物理学被认为是大量粒子的量子力学的极限。另一方面,经典力学源于相对论力学。例如,在狭义相对论的许多公式中,出现了一个修正因子 (v/c)2,其中 v 是物体的速度,c 是光速。对于比光速小得多的速度,我们可以忽略 c2 和更高次项。然后,这些公式简化为牛顿动能和动量的标准定义公式。因为狭义相对论必须与在低速下的牛顿力学相一致,所以这是应该的。计算机建模必须尽可能真实。经典物理学会像超流情况一样引入一个误差。为了产生可靠的世界模型,我们不能使用经典物理学。诚然,量子理论消耗时间和计算机资源,经典物理方程可以用来提供一个快速的解决方案,但这样的解决方案缺乏可靠性。
当试图描述一个物体的行为时,计算机建模将只使用能量标准来决定使用哪个理论:相对论还是量子论。在应用更精确的模型和进行计算之前,物理学家会使用经典模型来提供近似值。
在计算机模型中,如果排除经典物理学,就没有必要使用物体的速度。低能物体将由量子理论处理,高能物体将由相对论处理。[5][6][7]
4. 参考文献
[1] ^Weidner and Sells, Elementary Modern Physics Preface p.iii, 1968.
[2] ^Morin, David (2008). Introduction to Classical Mechanics. New York: Cambridge University Press. ISBN 9780521876223..
[3] ^Barut, Asim O. (1980) [1964]. Introduction to Classical Mechanics. New York: Dover Publications. ISBN 9780486640389..
[4] ^Einstein, Albert (2004) [1920]. Relativity. Robert W. Lawson. New York: Barnes & Noble. ISBN 9780760759219..
[5] ^Wojciech H. Zurek, Decoherence, einselection, and the quantum origins of the classical, Reviews of Modern Physics 2003, 75, 715 or https://arxiv.org/abs/quant-ph/0105127/.
[6] ^Wojciech H. Zurek, Decoherence and the transition from quantum to classical, Physics Today, 44, pp 36–44 (1991).
[7] ^Wojciech H. Zurek: Decoherence and the Transition from Quantum to Classical—Revisited Los Alamos Science Number 27 2002.