贡献者: certain_pineapple; addis
- 本文处于草稿阶段。
- 本文缺少预备知识,初学者可能会遇到困难。
- 注:本文中的自旋 $S$ 实际上为二倍的自旋,所以电子自旋被取值为 $\pm 1$,系数被吸纳入 $J$ 与 $B$ 中。
伊辛模型是用来描述铁磁现象的模型,其哈密顿量的形式为:
\begin{equation}
H=-J\sum\limits_{< i,j>}S_iS_j~.
\end{equation}
上式中的 $J$ 为交换耦合常数 $(J>0)$,$S_i$ 与 $S_j$ 是两原子的自旋,求和中的 $< i,j>$ 代表仅对最近邻的原子进行计算。
伊辛模型在一维和二维的情况下是可以严格求解的。在此介绍一维伊辛模型求解方法。
1. 一维伊辛模型求解
构建一维伊辛模型,并附以周期性边界条件,在外加磁场 $B$ 的情况下,模型的哈密顿量被写成:
\begin{equation}
H=-J\sum\limits_{i=1}^NS_iS_{i+1}-B\sum\limits_{i=1}^NS_i=-\sum\limits_{i=1}^N[JS_iS_{i+1}+B(S_i+S_{i+1})]~.
\end{equation}
上式中的 $BS_i$ 项中应为 $B\mu_i$,在此将玻尔磁子吸纳进 $B$ 的定义中。
写出配分函数:
\begin{align}
Z&=\sum\limits_{S_1,S_2,...S_N}exp\{\sum\limits_{i=1}^N\beta[JS_iS_{i+1}+B(S_i+S_{i+1})]\} \\
&=\sum\limits_{S_1,S_2,...S_N}\prod\limits_{i=1}^N exp\{\beta[JS_iS_{i+1}+B(S_i+S_{i+1})]\}~.
\end{align}
考虑:
\begin{equation}
\left\langle S_i \right\rvert P \left\lvert S_j \right\rangle =exp\{\beta[JS_iS_{j}+B(S_i+S_{j})]\}~,
\end{equation}
则有:
\begin{align}
Z&=\sum\limits_{S_1,S_2,...S_N}\prod\limits_{i=1}^N \left\langle S_i \right\rvert P \left\lvert S_i+1 \right\rangle \\
&=\sum\limits_{S_1,S_2,...S_N} \left\langle S_1 \right\rvert P \left\lvert S_2 \right\rangle \left\langle S_2 \right\rvert P \left\lvert S_3 \right\rangle \cdots \left\langle S_{N-1} \right\rvert P \left\lvert S_N \right\rangle ~.
\end{align}
考虑:
\begin{equation}
\sum_S \left\lvert S \right\rangle \left\langle S \right\rvert =\mathbb{1}~,
\end{equation}
则有:
\begin{equation}
Z=\sum\limits_{S_1} \left\langle S_1 \right\rvert P^N \left\lvert S_1 \right\rangle =tr(P^N)~.
\end{equation}
考虑 P 的矩阵元,由于 $S\in\{-1,1\}$,有:
$$P=\begin{pmatrix}
e^{\beta(J+B)},&e^{-\beta J} \\
~~e^{-\beta J}~~, & e^{\beta(J-B)}
\end{pmatrix}~.$$
计算得 $P$ 的本征值
$$\lambda=e^{\beta J}\cosh{(\beta B)}\pm \sqrt{e^{2\beta J }\sinh^2{(\beta B)}+e^{-2\beta J }}~.$$
则有:
\begin{align}
Z&=tr(P^N)=\lambda_1^N+\lambda_2^N \\~,
\lambda_1&=e^{\beta J}\cosh{(\beta B)}+ \sqrt{e^{2\beta J }\sinh^2{(\beta B)}+e^{-2\beta J }} \\~,
\lambda_2&=e^{\beta J}\cosh{(\beta B)}- \sqrt{e^{2\beta J }\sinh^2{(\beta B)}+e^{-2\beta J }}~.
\end{align}
则体系亥姆霍兹自由能 $F$:
$$F=-\beta^{-1}\ln{Z}=-\beta^{-1}\ln{(\lambda_1^N+\lambda_2^N)}=-N\beta^{-1}\ln{\lambda_1}-\beta^{-1}\ln[1+(\frac{\lambda_2}{\lambda_1})^N]~.$$
在通常情况下 $(B$ 和 $T$ 不全为 $0)$,有 $\lambda_1>\lambda_2$。所以在热力学极限下 $(N\rightarrow\infty)$,有:
$$F=-N\beta^{-1}\ln{\lambda_1}~.$$
可以求出平均自旋(此处 $B$ 包含玻尔磁子):
$$s=-\frac{1}{N}\frac{\partial F}{\partial B}=\frac{ \sinh\left(\beta B\right) }{\sqrt{\sinh^2(\beta B)+e^{-4\beta J}}}~.$$
绘制各种情况的图像。
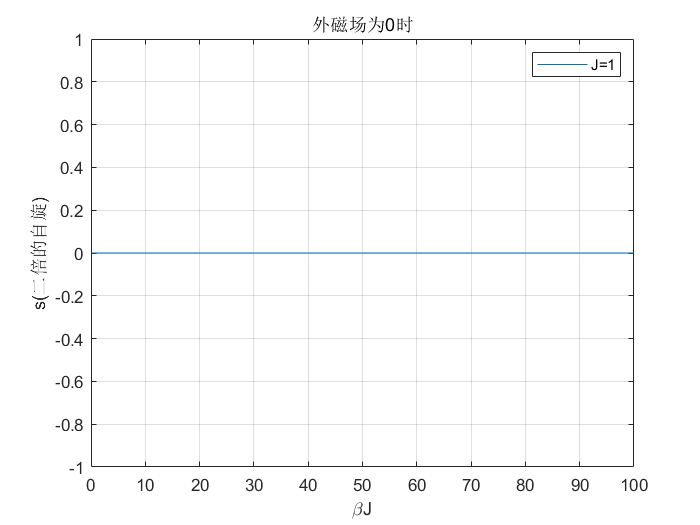
图 1:外磁场为 0 时
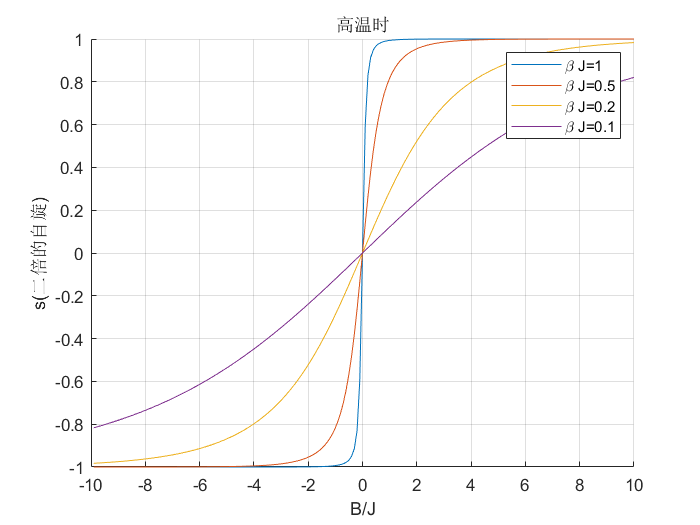
图 2:高温时
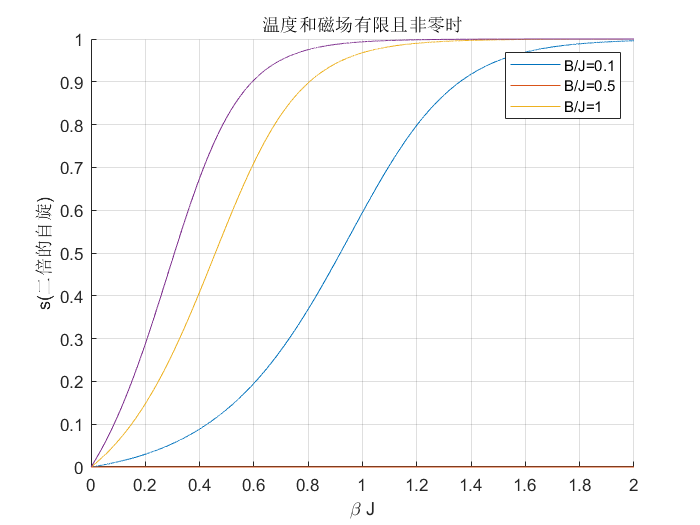
图 3:温度和磁场有限且非零时
横纵坐标的选取追求无量纲。
从图中可以看出,
在 $B\neq 0$ 时,$s$ 随温度连续变化。
在 $B=0$ 时,分两种情况,当 $T=0$ 时,$m$ 根据磁场趋向
于 0 的方向可分别取值 $\pm1$,当 $T\neq0$ 时,$s=0$。