哈希表(综述)
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译)
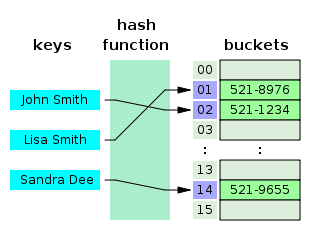
在计算领域中,哈希表(hash map)是一种实现关联数组抽象数据类型的数据结构,这种结构可以将关键码映射到给定值。哈希表使用哈希函数计算桶单元或槽位数组中的索引,从中可以找到所需的给定值。
理想情况下,哈希函数会将每个关键码分配给一个唯一的存储桶单元,但是大多数哈希表设计都使用不完美的哈希函数,这可能会导致哈希冲突,也就是哈希函数会为多个关键码生成相同的索引。这种冲突必须以某种方式解决。
在维度良好的哈希表中,每次查找的平均成本(指令数)与表中存储的记录个数无关。许多哈希表设计还允许任意插入和删除键值对,每次操作的平均成本(摊销[1])为常数。[2][3]
在许多情况下,哈希表比搜索树或任何其他表查找结构平均效率更高。因此,它们被广泛应用于多种计算机软件中,特别是用于关联数组、数据库索引、缓存和集合。
1. 哈希(散列)法
散列的概念是将条目(键/值对) 存储分布在桶单元数组中。设定一个关键码,用哈希算法计算一个索引,该索引建议在哪里可以找到条目:
散列的概念是将条目(键/值对) 存储分布在桶单元数组中。设定一个关键码,用哈希算法计算一个索引,该索引建议在哪里可以找到条目:
index = f(key, array_size)
hash = hashfunc(key)
index = hash % array_size
在数组大小是二的幂($n$ 次方)的情况下,剩余的操作被减少到屏蔽,这提高了速度,但是会增加散列函数性能不佳的问题。[5]
1.1 选择一个哈希(散列)函数
一个好的哈希函数和实现算法对于良好的哈希表性能至关重要,但可能难以实现。[6]
一个基本要求是哈希函数应该让哈希值均匀分布。非均匀分布增加了冲突的次数和解决冲突的成本。均匀性有时很难通过设计来保证,但可以使用统计检验方法进行经验评估,例如离散均匀分布的皮尔逊卡方检验。[7][8]
仅对于应用程序中出现的哈希表大小,才需要均匀分布。特别是,如果使用动态调整大小的操作,来使哈希表大小精确加倍和减半,那么只有当哈希表大小是二的幂(n 次方)时,哈希函数才需要一致。在这里,索引可以被计算为哈希函数的某个数位范围。另一方面,一些哈希算法更愿意哈希表的大小设定为质数,[9] 再由模数运算提供一些额外的混合操作;这对于一个设计不佳的哈希函数尤其有用。
对于开放式定址方案,散列函数还应该避免堆积现象的产生,即两个或多个关键码被映射到连续的槽位。这种堆积现象可能会导致查找成本急剧上升,即使这个哈希表的装填因子很低且冲突很少。流行的乘法哈希法[2] 据称很容易产生这类堆积现象。
通过使用模数约减或数位屏蔽技术,加密哈希函数可以为任何大小尺寸的哈希表提供良好的哈希函数。[9]如果存在恶意用户试图通过向服务器提交旨在哈希表中产生大量冲突的请求来破坏网络服务的风险,加密哈希函数也能进行适当的处理。当然,也可以通过更为简便的方法来避免这种恶意的风险(例如对数据进行秘密盐处理,或者使用通用散列函数)。加密哈希函数的缺点是计算速度通常较慢,这意味着对于任意大小的哈希表,在不强调均匀性是必须的情况下,非加密哈希函数可能是更好的选择。
1.2 完美散列函数
如果能提前知道所有的关键码,那么就可以使用一个完美的散列函数来创建一个没有冲突的完美哈希表。如果使用最小完美哈希,哈希表中的每个存储位置都可以得到使用。
完美的散列允许在所有情况下进行常数时间查找。这与大多数链接和开放式寻址方法形成对比,在这些方法中,平均查找时间很短。但当所有的关键码散列到几个给定值时,查找时间就可能非常长 O(n)。
2. 关键统计
关键码统计哈希表的一个关键统计数据是装填因子,定义为
- 其中 $n$ 是填入哈希表中记录个数(条目数)。
- $k$ 是桶的数量(哈希表的长度)。
随着装填因子的增大,哈希表的查找速度变得更慢,甚至可能无法工作(取决于所使用的方法)。哈希表的预期常数时间属性是假定装填因子保持在某个界限以下。因为桶的数量一般是固定的,查找时间随着条目数量的增加而增加,因此无法得到所需的常数时间。作为一个实际的应用例子,Java 10 程序语言中哈希表的默认装填因子是 0.75,这 “在查找时间和空间成本之间达到了一个很好的平衡”。[10]
其次,可以检查每个桶单元中条目数的差异。例如,两个表都有 1000 个条目和 1000 个桶,一个在每个桶中正好填有一个条目,另一个在同一个桶中填入所有条目。很明显,散列法在第二种情况下不起作用。
并不是装填因子低就特别有益。随着装填因子接近 0,哈希表中未使用区域的比例会增加,但搜索成本不一定会降低。这导致了内存的浪费。
3. 碰撞分辨率
冲突处理方法当散列一大组可能关键码的随机子集时,散列(哈希)冲突实际上是不可避免的。例如,如果将 2,450 个关键码散列到一百万个桶中,即使是完全均匀的随机分布,根据生日问题法则,至少有两个关键码散列到同一个槽位的概率大约为 95%。
因此,几乎所有哈希表实现都有一些冲突解决策略来处理这些事件。下面描述了一些常见的策略。所有这些方法都要求关键码(或指向它们的指针)与相关给定值一起存储在哈希表中。
3.1 独立链接
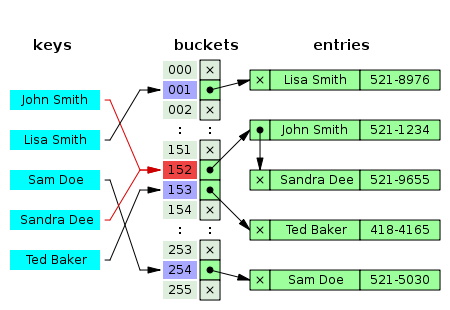
分离链接法在称为分离链接的方法中,每个桶单元都是独立的,并且有某种具有相同索引的条目列表。哈希表操作的时间是查找桶单元的时间(它是常数)加上遍历列表的时间。
在一个好的散列(哈希)表中,每个桶都有零个或一个条目,有时有两个或三个,但很少超过这个数量。因此,对于这些情况,在时间和空间上有效的结构是优先选择的。而对每个桶单元中相当多的条目都有效的结构并不需要或者不要求这样。如果这些情况经常发生,散列函数需要修复。
链接列表的单独链接
带有链表的分离链接法具有链表的链式哈希表很受欢迎,因为它们只需要具有简单算法的基本数据结构,并且可以使用不适合其他方法的简单哈希函数。
哈希表操作的成本是扫描所选存储桶的条目找到所需关键码的成本。如果关键码的分布足够均匀,查找的平均成本仅取决于每个桶所分布的关键码的平均数量,也就是说,它与装填因子大致成正比例关系。
因此,即使哈希表中条目数 $n$ 远远大于槽位数,链式哈希表仍然有效。例如,具有 1000 个插槽和 10,000 个存储关键码的链式哈希表(加载因子 10)比 10,000 个插槽的表(加载因子 1)慢五到十倍;但是仍然比普通的顺序列表快 1000 倍。
对于分离链接法,最坏的情况是所有条目都被插入到同一个桶中,在这种情况下哈希表是无效的,它的查找成本是遍历桶单元中所有数据结构。如果后者是一个线性列表,查找过程可能不得不扫描它的所有条目,因此这种最坏的情况下的查找时间成本也与表中条目的数量 $n$ 成正比例关系。
桶链通常使用条目添加到桶单元的顺序进行连续搜索。如果装填因子很大,并且某些关键码比其他关键码更有可能出现,那么使用向前移动启发式重新排列链可能是有效的。只有当装填因子很大(大约 10 或更多),或者如果散列分布可能非常不均匀,或者即使在最坏的情况下也要必须保证良好的性能时,才值得考虑使用更复杂的数据结构,例如平衡搜索树。然而,在那些情况下,使用更大的哈希表和/或更好的散列函数可能更有效。
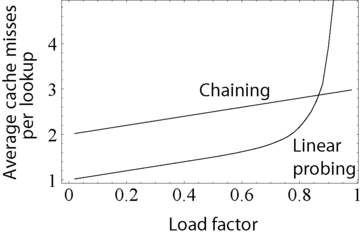
链式哈希表也继承了链表的缺点。当存储小键值对时,每个条目记录中下一个指针的空间开销可能很大。另一个缺点是遍历链表的缓存性能差,使得处理器缓存无效。
带有表头单元分离链接法
一些链接实现将每个链的第一条记录存储在自身的槽位数组中。[3]大多数情况下,指针遍历次数减少一次。目的是提高哈希表访问的缓存效率。
缺点是空桶占用的空间与只填入一个条目的桶相同。为了节省空间,这样的哈希表通常被分割成多个槽位,且槽位数量与存储条目数量一样多,这意味着许多槽位能够插入两个或更多条目。
与其他结构分开链接
带有其他数据结构的分离链接法我们可以使用支持所需操作的任何其他数据结构来代替列表。例如,通过使用自平衡二叉搜索树,理论上来讲,普通哈希表操作(插入、删除、查找)的最坏情况常数时间可以降低到 O(log n)而不是 O($n$)。但是,这给哈希表实现带来了额外的复杂性,并且可能会导致较小哈希表的性能更差,在这些哈希表中插入和平衡搜索树所需的时间大于对列表的所有元素执行线性搜索所需的时间。哈希表使用桶的自平衡二叉搜索树的一个现实例子是 Java 版本 8 中的哈希表类。[11]
称为数组哈希表的变型体使用动态数组来存储所有的条目,这些条目被散列到同一个槽位。[12][13][14] 每个新插入的条目都被附加到分配给插槽的动态数组的末尾。动态数组以精确匹配的方式调整大小,这意味着它只根据需要来增加字节的多少。人们发现,有些替代技术诸如通过块的大小或页面来增加数组可以提高插入性能,但需要更多的空间。这种变化更有效地利用了中央处理器缓存和转换后备缓冲器(TLB),因为插槽条目是按照顺序存储在内存中的。它还省去了链表所需的下一个指针,从而节省了空间。尽管频繁调整数组大小,但发现操作系统由此而产生的空间开销(如内存碎片)很小。
所谓的动态完美哈希对这种方法的使用进行了详细的说明,[15]其中包含 $k$ 个条目的桶被组织成一个具有 $k^2$ 个插槽位的完美哈希表。虽然它使用了更多的内存($n$ 个条目使用 $n^2$ 个插槽位,最坏情况下使用 $n\times k$ 个插槽位,平均情况下使用 $n\times k$ 个插槽),但这种变体保证了最坏情况下常数查找时间和较低的分摊插入时间。我们也可以为每个桶使用一个融合树数据结构,以高概率实现所有操作的常数时间。[16]
3.2 开放定址法主标题: 开放定址法
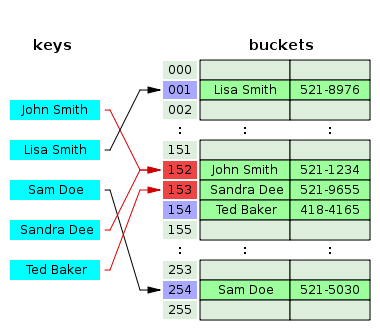
在另一种称为开放寻址的策略中另一个冲突解决策略是开放定址法,该方法将所有条目记录都存储在自身的桶单元数组中。当必须插入新条目时,将检查存储桶,从散列到插槽开始,并按一定的探测顺序进行,直到找到未占用的插槽位。当搜索条目时,以相同的顺序扫描存储桶,直至找到目标记录,或者找到未使用的槽位数组,这表明哈希表中没有这样的关键码。[17] 定名为 “开放寻址法” 是指明了一个事实,项目的位置(“地址”)不是由其哈希值决定的。这种方法也称为封闭散列法;它不应该与通常意味着分离链接法的 “开放散列” 或 “封闭寻址” 混淆。
众所周知的探测法序列包括:
- 线性探测,其中探测位置之间的间隔是固定的(通常为 1)
- 二次探测,通过将二次多项式的连续输出与原始散列计算给出的初始值相加来增加探测之间的位置间隔
- 双重散列法,其中探测之间的位置间隔由第二个散列函数计算
所有这些开放寻址方案的缺点是存储条目的数量不能超过存储桶阵列中的插槽数量。事实上,即使有好的散列(哈希)函数,当装填因子超过 0.7 左右时,它们的性能也会显著下降。对于许多应用程序来说,这些限制要求使用动态调整大小,随之而来的是成本上升。
开放寻址方案也对散列函数提出了更严格的要求:除了要求在桶上更均匀地分配关键码之外,该函数还必须将按照顺序探测连续的散列值的堆积最小化。在使用分离链接法的过程中,唯一要关心的是太多的目标映射到同一个哈希值;而不管它们是相邻的还是邻近的都完全无关紧要。
只有当条目很小(小于指针大小的四倍)并且装填因子不太小时,开放式寻址才能节省内存。如果装填因子接近于零(即桶单元数比存储的条目多得多),开放寻址是浪费的,即使每个条目只有两个字。
开放寻址避免了分配每个新条目记录的时间开销,甚至可以在没有内存分配器的情况下实现。它还避免了访问每个桶的第一个条目(通常是唯一的一个)所需的额外间接操作。它还具有更好的参考局部性,特别是线性探测。对于较小的记录,这些因素可以产生比链接更好的性能,特别是执行查找操作的时候。具有开放寻址的哈希表也更容易序列化,因为它们不使用指针。
另一方面,当需要存储的条目数量很大时,普通的开放寻址是一个糟糕的选择,因为这些条目会填满整个 CPU 高速缓存行(抵消了高速缓存的优势),出现了大量的空槽位,因而浪费了大量的存储空间。如果开放寻址表只存储对元素的引用(外部存储),即使是处理大量的条目记录,它也会使用与链接相当的空间,但会失去速度优势。一般来说,开放寻址更适用于那些具有较少条目记录的哈希表,这些较少的条目记录可以存储在哈希表中(内部存储)并适合缓存行。它们特别适合处理只有一个单词或更少的条目记录。如果希望哈希表具有高装填因子,需要处理的记录也很大,或者数据大小可变,那么使用链式哈希表的性能通常也一样或更好。
合并链接散列法
这是一种将链接和开放寻址混合在一起的方法,合并散列将表本身内的节点链接在一起。[17] 像开放寻址一样,它实现了较好空间使用和只比单纯链接稍微减少一点的缓冲优势。像链接一样,它也不会出现象堆积效应;事实上,哈希表可以被高中密度过地有效填充。与单纯链接不同,它要处理的条目记录数不能多于表中的槽位数。
布谷鸟散列(哈希)法
另一种开放寻址解决方案是布谷鸟散列法,它确保在最坏的情况下查找时间不变,插入和删除的摊销时间不变。它使用两个或多个散列函数,这意味着任何键/值对都可以位于两个或多个位置。执行查找时,使用第一个散列函数,如果找不到键/值,则使用第二个散列函数,依此类推。如果在插入过程中发生冲突,则使用第二个散列函数对关键码进行重新散列,以将其映射到另一个桶。如果所有散列函数都已使用,但仍存在冲突,则它所冲突的关键码将被移出,为新的关键码腾出空间,旧关键码将用其他散列函数之一重新散列,从而将其映射到另一个桶。如果该位置也导致冲突,则重复该过程,直到没有冲突或该过程遍历所有存储桶,在此次过程中哈希表被调整大小。通过将多个散列函数与每个桶中的多个单元相结合,可以实现非常高的空间利用率。
跳房子散列(哈希)法
另一种可供选择优的开放寻址的解决方案是跳房子散列法,[18] 它结合了布谷鸟散列法和线性探测法,但似乎总体上又避免了它们的局限性。特别是,即使装填因子超过 0.9,它也能很好地工作。该算法非常适合实现可调整大小的并发哈希表。
跳房子哈希算法通过在原始哈希桶附近定义一个邻域来工作,在该邻域中总是可以找到给定的条目。因此,搜索限于该邻域中的条目数,在最坏的情况下这个邻域范围内的条目数量成对数关系分布,确保最坏平均查询时间为常数,并且邻域中的条目正确对齐通常需要一次高速缓存缺失。插入条目时,首先尝试将其添加到邻域范围内的桶中。然而,如果该邻域中的所有桶都被占用,则该算法将依次遍历所有桶单元,直到找到一个开放的槽位(未被占满的桶)(与线性探测一样)。此时,由于空桶在邻域区域之外,它们会以一系列跳跃重复移动。(这类似于布谷鸟散列法,但不同之处在于,在这种情况下,空槽被移动到邻近区域,而不是为了最终找到空槽而将项目移出。)每一跳都会使开放槽更靠近原始邻域,而不会使沿途任何桶的邻域属性无效。最后,开放的插槽位已经被移动到邻域范围内,正等着被插入的条目就可以被添加到其中。
3.3 罗宾汉散列(哈希法)
双哈希冲突解决方案的一个有趣变化是罗宾汉哈希。[19][20] 其设计思路是,如果一个新的关键码的探测次数大于当前位置的关键码的探测次数,它可能会替换已经插入的关键码。这样做的最终效果是减少了表格[21] 中最坏情况的搜索时间。这类似于有序散列表,除了碰撞键的标准不依赖于键之间的直接关系。由于出现最坏的情况概率和探针数量的变化都显著减少,一个有趣的变化是哈希表探测可以从预期的成功探测值开始,然后从该位置向两个方向扩展。[22]外部罗宾汉散列法(External Robin Hood hashing)是这种算法的扩展,哈希表存储在一个外部文件中,每个表位置对应于一个固定大小的页面或者记录为 B 的桶单元。[23]
3.4 双选择散列法
2-choice 哈希为哈希表使用两种不同的哈希函数 $h1(x)$ 和 $h2(x)$。两个散列函数都用于计算两个表位置。当一个目标条目插入表中时,它将被放置在包含较少条目的哈希表内(如果桶大小相等,默认为 h1(x)表位置)。双选择散列法利用了两个选择的幂(2 的 n 次方)的原理。
4. 动态调整大小
当插入使得哈希表中的条目数超过装填因子和当前容量的乘积时,则需要重新散列哈希表。[10] 重新散列包括增加底层数据结构的大小,[10] 并将现有条目映射到新的存储桶位置。在一些实现中,如果初始容量大于最大条目数除以装填因子,则不需要进行再散列操作。[10]
为了限制因空置的存储桶而浪费的内存比例,一些实现还会在删除项目时缩小哈希表的大小,而接下来在进行条目删除的时候进行重新哈希。从空间-时间权衡的角度来看,这个操作类似于动态数组中重新分配储存地址。
4.1 通过复制所有条目来调整大小
一种常见的方法是,当装填因子超过某个阈值 rmax 时,自动触发一个完整的调整大小操作。然后分配一个新的更大容量的哈希表,从旧表中移出每个条目,并插入到新表中。当所有条目都从旧表中移出后,旧表将返回到空闲存储池。与此相对应地,当装填因子低于第二阈值 rmin 时,所有条目都被移动到一个新的较小的表中。
对于频繁收缩和增长的哈希表,可以完全跳过向下调整大小。在这种情况下,表的大小与哈希表中一次出现的最大条目数成正比例关系,而不是与当前条目数成比例。缺点是内存使用率会更高,因此缓存行为可能会更差。为了获得最佳控制,可以提供 “收缩到合适” 操作,仅在需要时才这样做。
如果每次扩展时表的大小增加或减少一个固定的百分比,那么这些重新调整的总成本,在所有插入和删除操作中摊销,仍然是一个常数,与条目数量 n 和执行的操作次数 m 无关。
例如,我们假设新创建一个哈希表,这个表的尺寸尽可能小,每当装填因子超过某个阈值时,该表的大小就会加倍。如果 m 个条目被插入到该表中,则在表的所有动态调整大小中发生的额外重新插入的总数最多为 m-1。换句话说,动态调整大小会使每次插入或删除操作的成本增加一倍。
4.2 一步到位重新哈希的替代方案
一些哈希表的实现,尤其是在实时系统中,无法做到一次性扩大哈希表,因为这会中断对时序要求严格的操作。如果无法避免动态调整大小,解决方案是逐步执行调整大小操作。
基于磁盘的哈希表几乎总是使用一些替代方法来替代这种一次性重新散列法,因为在磁盘上重建整个表的成本太高。
增量调整大小
一种方法是逐步执行重新散列:
- 在调整大小期间,分配新哈希表,但保持旧表不变
- 在每次查找或删除操作中,两个表都要检查
- 仅在新表中执行插入操作
- 每次插入时,还要将 r 元素从旧表移动到新表
- 当从旧表中移出所有元素时,应将其释放
为了确保在需要扩大新表之前完全复制旧表,有必要在调整大小的过程中将表的大小至少增加 $(r + 1)/r$。
单调键
单调性关键码如果知道键值总是单调的增加(或减少),那么通过在每个哈希表调整大小操作中保持单个最近键值的列表,可以实现一致性哈希算法的变化。查找时,在这些列表条目定义的范围内的关键码被导引到适当的哈希函数,实际上是哈希表,对于每个范围,这两者都可能不同。由于将条目总数增加一倍是很常见的,所以只需要检查 O(log($N$))范围,重定向的二进制搜索时间为 O(log(log($N$))))。与一致性哈希算法一样,这种方法保证任何关键码的哈希一旦发布,将永远不会改变,即使哈希表后来增长了。
线性散列(哈希)法
线性哈希[24] 是一种允许逐步扩展的哈希表算法。它使用单个哈希表实现,但是有两个可能的查找函数。
分布式哈希表的哈希法
降低哈希表大小调整成本的另一种方法是选择一个散列函数,使大多数给定值的散列在哈希表大小调整时不会改变。这种散列函数在基于磁盘的分布式哈希表中非常普遍,在这些哈希表中,重新散列的成本非常高。设计哈希表以使大多数给定值在调整表大小时不变的问题被称为分布式哈希表问题。四种最常见的方法是集合散列法、一致性散列法、内容可寻址网络算法和卡德米利亚洲 Kademlia 距离算法。
5. 技术性能分析
在最简单的模型中,散列函数是完全未指定的,并且未调整大小。有了一个理想的散列函数,一个大小的表 $k$,开放寻址没有冲突,并且支持 $k$ 元素进行单次成功查找,而表的大小 $k$ 带链接和 $n$ 键是最少 $max(0,n-k)$ 碰撞和 $\Theta(1+\frac{n}{k})$ 查找比较。对于最坏的散列函数,每次插入都会导致冲突,哈希表退化为线性搜索 $\Theta(n)$ 每次插入的碰撞比例,最高可达 $n$ 成功查找的比较。
将重新散列列添加到这个模型中很简单。就像在一个动态数组中,几何尽寸调整因子为 $b$ 意味着 $\frac{n}{b^i}$ 插入键匙 $i$ 或更多次,因此插入的总数以 $$\frac{bn}{b-1}~$$,这是 $\Theta(n)$。这通过使用 rehashing 来维持 $n< k$,同时使用链接和开放寻址的表可以有无限的元素,并在单次比率成功找到散列列函数的最佳选择。
在更现实的模型中,散列函数是散列列函数的概率分布的随机变量,并且在散列列函数的选择上平均计算性能。当这个分布是均匀的时,这个假设被称为 “简单统一散列”,并且可以证明使用链接散列列函数需要 $$\Theta(\frac{1}{1-n/k})~$$ 查找不成功的平均比较,以及使用开放寻址的哈希需要 $\frac{n}{k}< c$ 不变,则这两个边界是常量,其中 $c$ 是小于 1 的固定常数。
$$\Theta(1+\frac{n}{k})~$$
6. 特征
6.1 优势
- 哈希表相对于其他表数据结构的主要优势是速度。当条目数量较大时,这一优势更加明显。当可以预先预测最大条目数时,哈希表特别有效,因此桶数组可以以最合适的规模一次性分配,并且再也不会重新调整。
- 如果键-值对的集合是固定的并且提前知道(因此不允许插入和删除),可以通过仔细选择散列函数、桶表大小和内部数据结构来降低平均查找成本。尤其特别的是,人们可以设计一个无冲突甚至完美的散列函数。在这种情况下,关键码不需要存储在表中。
6.2 缺点
- 虽然哈希表的操作只需要平均常数时间,但是即便一个好的哈希函数的成本也可能远远高于顺序列表或搜索树的查找算法的内部循环。因此,当条目数量非常少时,哈希表是无效的。(然而,在某些情况下,散列函数计算的高成本可以通过将散列值与关键码一起保存来降低。)
- 对于某些特定的字符串处理应用程序,如拼写检查,散列表可能不如尝试单词查找树(Tries)、有限自动机或朱迪数组有效。此外,如果没有太多可能的关键码要存储,也就是说,如果每个关键码可以用足够少的位数来表示,那么可以直接使用关键码作为给定值数组的索引,而不是哈希表。请注意,在这种情况下没有冲突。
- 存储在哈希表中的条目可以被有效地枚举(以每个条目的恒定成本),但是只能以某种伪随机顺序。因此,没有一个有效的方法来定位其关键码最接近给定关键码的条目。以特定顺序列出所有 n 个条目通常需要单独的排序步骤,其成本与每个条目的) log(n)成比例。相比之下,有序搜索树的查找和插入成本同样与 log(n)成比例,但却能够以大约相同的成本找到最近的关键码,并以每个条目的恒定成本对所有条目进行有序枚举。
- 如果关键码没有被存储(因为散列函数是无冲突的),可能没有简单的方法来枚举在任何给定时刻出现在表中的关键码。
- 虽然每次操作的平均成本是恒定的,并且相当小,但是单次操作的成本可能还是相当高。特别是,如果哈希表使用动态调整大小,插入或删除操作有时会占用与条目数量成比例的时间。这在实时或交互式应用中可能是一个严重的缺陷。
- 哈希表通常表现出较差的访问局部性,也就是说,要访问的数据似乎是随机分布在内存中的。因为散列表会导致访问模式出现跳跃性,这可能会触发微处理器缓存缺失,从而导致长时间延迟。如果哈希表相对较小并且关键码排列比较紧凑,这种紧凑的数据结构(例如用线性搜索搜索的数组)可能会更快。最佳性能点因系统而异。
- 当有许多冲突时,哈希表就会表现得非常低效。虽然极不均匀的散列分布状况极不可能偶然出现,但是知道散列函数的恶意对手可能会向哈希表提供错误信息,从而通过引起过度冲突而产生最坏情况的行为,导致哈希表出现非常差的性能,例如拒绝服务攻击。[26][27][28] 在关键应用程序中,可以使用具有更好最坏情况保证的数据结构;然而,采用通用散列法——一种防止攻击者预测哪些输入会导致最坏情况的随机算法——可能更可取。[29]Linux 路由表缓存中哈希表使用的哈希函数在 Linux 版本 2.4.2 中进行了更改,以此作为抵御此类攻击的对策。[30]
7. 使用
7.1 用途关联数组
哈希表通常用于实现许多类型的内存表。它们用于实现关联数组(其索引是任意字符串或其他复杂对象的数组),尤其是在像 Ruby、Python 和 PHP 这样的解释型编程语言中。
当将新项目存储到多重映射器(multimap)中并且发生哈希冲突时,multimap 无条件地存储这两个项目。
当将新条目存储到典型的关联数组中时,也会发生哈希冲突,但是实际的关键码本身是不同的,关联数组同样会存储这两个条目。但是,如果新项目的关键码与旧项目的关键码完全匹配,关联数组通常会擦除旧条目并用新条目覆盖它,因此表中的每个条目都有唯一的关键码。
7.2 数据库索引
哈希表也可以用作基于磁盘的数据结构和数据库索引(例如在 dbm 中),尽管 B 树在这些应用中更受欢迎。在多节点数据库系统中,哈希表通常用于在节点之间进行行数分配,从而减少哈希连接的网络流量。
7.3 缓存主标题缓存(计算)
哈希表可用于实现缓存,即辅助数据表,用于加速对主要存储在较慢介质中的数据的访问。在这个应用程序中,散列冲突可以通过丢弃两个冲突条目中的一个来处理——通常擦除当前存储在表中的旧条目并用新条目覆盖它,因此表中的每个条目都有唯一的散列值。
7.4 设置
集合除了恢复具有给定关键码的条目之外,许多哈希表实现还可以判断这样的条目是否存在。
因此,这些结构可用于实现一组数据结构集合,该数据结构仅记录给定关键码是否属于指定的关键码集合。在这种情况下,可以通过消除与条目值相关的所有部分来简化结构。哈希可以用来实现静态和动态集合。
7.5 对象表示
几种动态语言,如 Perl、Python、JavaScript、Lua 和 Ruby,使用哈希表来实现对象。在这个表示中,键是对象的成员和方法的名称,值是指向相应成员或方法的指针。
7.6 独特的数据表示
一些程序可以使用哈希表来避免创建多个具有相同内容的字符串。为此,程序使用的所有字符串都存储在作为哈希表实现的单个字符串池中,每当需要创建新字符串时都会检查哈希表。这种技术是在 Lisp 解释器中以 hash consing 的名称引入的,并且可以与许多其他类型的数据(符号代数系统中的表达式树、数据库中的记录、文件系统中的文件、二进制决策图等)一起使用。
8. 实现
8.1 实现在编程语言中
许多编程语言提供哈希表功能,或者作为内置关联数组,或者作为标准库模块。例如,在 C++11 中,无序映射类为任意类型的键和值提供哈希表。
Java 编程语言(包括安卓上使用的变体)包括 HashSet、HashMap、LinkedHashSet、LinkedHashMap 通用集合。[31]
在 PHP 5 和 7 中,Zend 2 引擎和 Zend 3 引擎(分别)使用丹尼尔·伯恩斯坦(Daniel J. Bernstein)的散列函数之一来生成散列值用于管理存储在散列表中的数据指针的映射。在 PHP 源代码中,它被标记为 DJBX33A。
Python 以 dict 类型形式的内置哈希表实现以及 Perl 的哈希类型(%)在内部用于实现名称空间,因此需要更加关注安全性,即冲突攻击。Python 集还在内部使用散列,以便快速查找(尽管它们只存储键,而不存储值)。[32]
在.NET 框架中,哈希表的支持是通过存储键值对的非通用哈希表和通用字典类以及仅存储值的通用哈希表类来提供的。
在 Rust 的标准库中,通用哈希映射(HashMap)和哈希集合(HashSet)结构使用罗宾汉存储桶盗窃方式的线性探测法。
ANSI Smalltalk 定义类集/标识符集和字典/标识符字典。所有 Smalltalk 实现都提供了 WeakSet、WeakKeyDictionary 和 WeakValueDictionary 的附加(尚未标准化)版本。
9. 发展历史
哈希的概念在不同的地方独立产生。1953 年 1 月,汉斯·彼得·卢恩写了一份内部的 IBM 备忘录,使用散列和链接。[33] 吉恩·阿姆达尔、伊莱恩·麦格劳、纳撒尼尔·罗彻斯特和亚瑟·塞缪尔几乎同时使用哈希算法实现了一个程序。线性探测的开放式寻址(相对初级的阶段)被认为是阿姆达尔的功劳,但埃尔绍夫(俄国)在当时也有同样的想法。[33]
9.1 相关数据结构
有几种数据结构使用哈希函数,但不能被视为哈希表的特殊情况:
- 布隆过滤器,为恒定时间近似查找而设计的高效存储数据结构;使用哈希函数,可以被视为近似哈希表。
- 分布式哈希表 (分布式哈希表),一种分布在网络几个节点上的弹性动态表。
- 哈希数组映射 trie,a trie 结构,类似于 数组映射 trie,但是每个键首先被散列
10. 参考文献
[1] ^Charles E. Leiserson, Amortized Algorithms, Table Doubling, Potential Method Archived 8 月 7, 2009 at the Wayback Machine Lecture 13, course MIT 6.046J/18.410J Introduction to Algorithms—Fall 2005.
[2] ^Knuth, Donald (1998). 'The Art of Computer Programming'. 3: Sorting and Searching (2nd ed.). Addison-Wesley. pp. 513–558. ISBN 0-201-89685-0..
[3] ^Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2001). "Chapter 11: Hash Tables". Introduction to Algorithms (2nd ed.). MIT Press and McGraw-Hill. pp. 221–252. ISBN 978-0-262-53196-2..
[4] ^Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009). Introduction to Algorithms (3rd ed.). Massachusetts Institute of Technology. pp. 253–280. ISBN 978-0-262-03384-8..
[5] ^"JDK HashMap Hashcode implementation". Archived from the original on May 21, 2017..
[6] ^"python/cpython". GitHub (in 英语). Retrieved 2018-09-19..
[7] ^Pearson, Karl (1900). "On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling". Philosophical Magazine. Series 5. 50 (302). pp. 157–175. doi:10.1080/14786440009463897..
[8] ^Plackett, Robin (1983). "Karl Pearson and the Chi-Squared Test". International Statistical Review (International Statistical Institute (ISI)). 51 (1). pp. 59–72. doi:10.2307/1402731..
[9] ^Wang, Thomas (March 1997). "Prime Double Hash Table". Archived from the original on 1999-09-03. Retrieved 2015-05-10..
[10] ^Javadoc for HashMap in Java 10 https://docs.oracle.com/javase/10/docs/api/java/util/HashMap.html.
[11] ^"How does a HashMap work in JAVA". coding-geek.com. Archived from the original on November 19, 2016..
[12] ^Askitis, Nikolas; Zobel, Justin (October 2005). Cache-conscious Collision Resolution in String Hash Tables. Proceedings of the 12th International Conference, String Processing and Information Retrieval (SPIRE 2005). 3772/2005. pp. 91–102. doi:10.1007/11575832_11. ISBN 978-3-540-29740-6..
[13] ^Askitis, Nikolas; Sinha, Ranjan (2010). "Engineering scalable, cache and space efficient tries for strings". The VLDB Journal. 17 (5): 633–660. doi:10.1007/s00778-010-0183-9. ISSN 1066-8888..
[14] ^Askitis, Nikolas (2009). Fast and Compact Hash Tables for Integer Keys (PDF). Proceedings of the 32nd Australasian Computer Science Conference (ACSC 2009). 91. pp. 113–122. ISBN 978-1-920682-72-9. Archived (PDF) from the original on February 16, 2011..
[15] ^Erik Demaine, Jeff Lind. 6.897: Advanced Data Structures. MIT Computer Science and Artificial Intelligence Laboratory. Spring 2003. "Archived copy" (PDF). Archived (PDF) from the original on June 15, 2010. Retrieved June 30, 2008.CS1 maint: Archived copy as title (link).
[16] ^Willard, Dan E. (2000). "Examining computational geometry, van Emde Boas trees, and hashing from the perspective of the fusion tree". SIAM Journal on Computing. 29 (3): 1030–1049. doi:10.1137/S0097539797322425. MR 1740562...
[17] ^Tenenbaum, Aaron M.; Langsam, Yedidyah; Augenstein, Moshe J. (1990). Data Structures Using C. Prentice Hall. pp. 456–461, p. 472. ISBN 0-13-199746-7..
[18] ^Herlihy, Maurice; Shavit, Nir; Tzafrir, Moran (2008). "Hopscotch Hashing". DISC '08: Proceedings of the 22nd international symposium on Distributed Computing. Berlin, Heidelberg: Springer-Verlag. pp. 350–364. CiteSeerX 10.1.1.296.8742..
[19] ^Celis, Pedro (1986). Robin Hood hashing (PDF) (Technical report). Computer Science Department, University of Waterloo. CS-86-14. Archived (PDF) from the original on July 17, 2014..
[20] ^Goossaert, Emmanuel (2013). "Robin Hood hashing". Archived from the original on March 21, 2014..
[21] ^Amble, Ole; Knuth, Don (1974). "Ordered hash tables". Computer Journal. 17 (2): 135. doi:10.1093/comjnl/17.2.135..
[22] ^Viola, Alfredo (October 2005). "Exact distribution of individual displacements in linear probing hashing". Transactions on Algorithms (TALG). ACM. 1 (2, ): 214–242. doi:10.1145/1103963.1103965..
[23] ^Celis, Pedro (March 1988). External Robin Hood Hashing (Technical report). Computer Science Department, Indiana University. TR246..
[24] ^Litwin, Witold (1980). "Linear hashing: A new tool for file and table addressing". Proc. 6th Conference on Very Large Databases. pp. 212–223..
[25] ^Doug Dunham. CS 4521 Lecture Notes Archived 7 月 22, 2009 at the Wayback Machine. University of Minnesota Duluth. Theorems 11.2, 11.6. Last modified April 21, 2009..
[26] ^Alexander Klink and Julian Wälde's Efficient Denial of Service Attacks on Web Application Platforms Archived 9 月 16, 2016 at the Wayback Machine, December 28, 2011, 28th Chaos Communication Congress. Berlin, Germany..
[27] ^Mike Lennon "Hash Table Vulnerability Enables Wide-Scale DDoS Attacks" Archived 9 月 19, 2016 at the Wayback Machine. 2011..
[28] ^"Hardening Perl's Hash Function". November 6, 2013. Archived from the original on September 16, 2016..
[29] ^Crosby and Wallach. Denial of Service via Algorithmic Complexity Attacks Archived 3 月 4, 2016 at the Wayback Machine. quote: "modern universal hashing techniques can yield performance comparable to commonplace hash functions while being provably secure against these attacks." "Universal hash functions ... are ... a solution suitable for adversarial environments. ... in production systems.".
[30] ^Bar-Yosef, Noa; Wool, Avishai (2007). Remote algorithmic complexity attacks against randomized hash tables Proc. International Conference on Security and Cryptography (SECRYPT) (PDF). p. 124. Archived (PDF) from the original on September 16, 2014..
[31] ^"Lesson: Implementations (The Java™ Tutorials > Collections)". docs.oracle.com. Archived from the original on January 18, 2017. Retrieved April 27, 2018..
[32] ^"Python: List vs Dict for look up table". stackoverflow.com. Archived from the original on December 2, 2017. Retrieved April 27, 2018..
[33] ^Mehta, Dinesh P.; Sahni, Sartaj. Handbook of Datastructures and Applications. p. 9-15. ISBN 1-58488-435-5..