核聚变
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译)
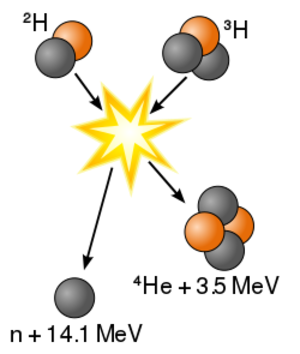
在核化学中,核聚变是两个或两个以上的原子核结合形成一个或多个不同的原子核和亚原子粒子(中子或质子)的反应。反应物和产物之间的质量差异表现为能量的释放或吸收。这种质量差异是由于反应前后原子核之间原子 “结合能” 的差异引起的。聚变是为活跃的或 “主序” 恒星或其他高星等恒星提供能量的过程。
产生比铁-56 或镍-62 更轻的原子核的聚变过程通常会产生净能量释放。这些元素每个核子的质量最小,每个核子的结合能最大。轻元素向这些方向的聚变释放能量(放热过程),而产生比这些元素更重的原子核的聚变将导致产生的核子保留能量,而产生的反应是吸热的。相反的情况适用于相反的过程,核子裂变。这意味着较轻的元素,如氢和氦,通常更易聚变;而较重的元素,例如铀,钍和钚,更容易裂变。极端天体物理学的事件例如超新星能产生足够的能量将原子核融合成比铁还重的元素。
1920 年,亚瑟·爱丁顿提出氢氦聚变可能是恒星能量的主要来源。1929 年弗里德里希·洪德(Friedrich Hund)发现了量子隧穿现象,不久之后,罗伯特·阿特金森(Robert Atkinson)和弗里茨·霍特曼斯(Fritz Houtermans)利用测量到的轻元素质量,证明了融合小原子核可以释放出大量能量。在欧内斯特•卢瑟福(Ernest Rutherford)早期核嬗变实验的基础上,1932 年,马克•奥列芬特(Mark Oliphant)在实验室完成了氢同位素的融合。在那十年剩下的时间里,汉斯·贝特(Hans Bethe)提出了恒星核聚变主要周期的理论。为军事目的而进行的核聚变研究始于 20 世纪 40 年代初,是曼哈顿计划(Manhattan Project)的一部分。核聚变是在 1951 年的温室项目核试验中完成的。1952 年 11 月 1 日,在一次爆炸中进行了大规模的核聚变实验。。
自 20 世纪 40 年代以来,在聚变反应堆内开发受控聚变的研究一直在进行,但该技术仍处于发展阶段。。
1. 过程
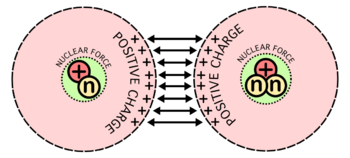
轻元素聚变释放能量是由于两种相反力的相互作用:一种是将质子和中子结合在一起的核力,另一种是导致质子相互排斥的库仑力。质子带正电荷,在库仑力的作用下相互排斥,但它们仍然可以粘在一起,这证明了另一种短程力的存在,这种力被称为原子核引力。[1]轻核(或比铁和镍小的核)足够小,质子较少,允许核力克服库仑力排斥作用。这是因为原子核足够小,所有的核子都感受到短程吸引力,它们所受的核力与受到的无限程库仑排斥力一样强烈。通过核聚变从较轻的原子核构建原子核,会从粒子的净吸引力中释放额外的能量。然而,对于较大的原子核,没有能量释放,因为核力是短程的,并且不能在较长的核长度尺度上继续作用。因此,能量不会随着这种原子核的融合而释放;相反,这些过程需要能量作为输入。
核聚变为恒星提供能量,并在一个叫做核合成的过程中产生几乎所有的元素。太阳是一颗主序星,因此,它的能量来自于氢核与氦的核聚变。在其核心,太阳每秒融合 6.2 亿吨氢,每秒产生 6.06 亿吨氦。恒星中较轻元素的融合释放出能量质量。例如,在两个氢核融合形成氦的过程中,0.7%的质量以 $\alpha$ 粒子动能或其他形式的能量(如电磁辐射)的形式被带走。[2]
迫使原子核融合需要相当大的能量,即使是最轻的元素——氢。当加速到足够高的速度时,原子核可以克服这种静电斥力,并靠得足够近,使得吸引力核力大于排斥库仑力。一旦原子核足够接近,强力会迅速增长,聚变的核子实质上就会 “落入” 彼此之中,其结果就是聚变和产生的净能量。较轻原子核的融合产生了较重的原子核,通常还会产生一个自由的中子或质子,而且释放的能量比迫使原子核聚合所需的能量要多;这是一个可以产生自我维持反应的放热过程。
大多数核反应释放的能量比化学反应大得多,因为把原子核结合在一起的结合能比把电子结合在原子核上的能量大。例如,在氢原子核中加入一个电子所获得的电离能是 13.6 ev,比图中所示的氘-氚(D-T)反应所释放的 17.6 MeV 的百万分之一还少;聚变反应的能量密度比核裂变大很多倍;这些反应每单位质量产生的能量要大得多,尽管个别的裂变反应通常比个别的聚变反应能量大得多,而聚变反应本身的能量是化学反应的几百万倍。只有直接将质量转化为能量,例如由物质和反物质的湮灭碰撞所引起的能量,在单位质量上才比核聚变具有更高的能量。(完全转换一克物质会释放出 9×1013 焦耳的能量。)
利用核聚变发电的研究已经进行了 60 多年。受控聚变的成功实现一直受到科技难题的阻碍;尽管如此,已经取得了重要进展。目前,受控聚变反应还不能产生 “保本的”(自维持)受控聚变。最先进的两种方法是磁约束(环形设计)和惯性约束(激光设计)。
理论上,环形反应堆的聚变能量是将等离子体加热到所需温度所需能量的 10 倍,这种反应堆的可行设计正在开发中。ITER 设施预计将在 2025 年完成建设阶段。它将在同年开始运行该反应堆,并在 2025 年启动等离子体实验,但预计要到 2035 年才能开始完全氘氚融合。[3]
美国国家点火装置使用激光驱动惯性约束核聚变,旨在实现核聚变的收支平衡;第一次大规模的激光目标实验于 2009 年 6 月进行,点火实验于 2011 年初开始。[4][5]
2. 恒星中的核聚变
一个重要的聚变过程是为恒星(如太阳)提供能量的恒星核合成。二十世纪,人们认识到核聚变反应释放的能量造成恒星释放热和光的原因。恒星中的原子核融合从最初的氢和氦丰度开始,提供这种能量,并作为融合过程的副产品合成新的原子核。不同的反应链涉及,取决于恒星的质量(因此也取决于其核心的压力和温度)。
1920 年左右,亚瑟·爱丁顿在他的论文中《恒星的内部结构》预测了恒星的核聚变过程的发现和机制。[6][7]当时,恒星能量的来源完全是个谜;爱丁顿正确地推测了氢融合成氦的来源,根据爱因斯坦方程,释放出巨大的能量 $E = mc^2$。这是一个特别显著的发展,因为当时聚变和热核能,甚至恒星主要由氢组成,还没有被发现。爱丁顿的论文基于当时的知识,推论道:
- 恒星能量的主要理论,即收缩假说,由于角动量守恒,应该会使恒星的自转明显加快。但是对造父变星的观察表明,这并没有发生。
- 唯一已知的其他似乎可信的能源是物质向能量的转化;爱因斯坦几年前就已经证明,少量的物质等于大量的能量。
- 弗朗西斯·阿斯顿(Francis Aston)最近还发现,一个氦原子的质量大约比四个氢原子结合形成一个氦原子的质量低 0.8%,这表明,如果这种结合能够发生,它将作为一种副产品释放出相当大的能量。
- 如果一颗恒星只含有 5%的可熔氢,这就足以解释恒星是如何获得能量的。(我们现在知道,大多数‘普通’恒星的氢含量远远超过 5%)
- 其他的元素也可能被融合,其他科学家推测,恒星是轻元素结合产生重元素的 “坩埚”,但如果没有对它们的原子质量进行更精确的测量,当时就什么也说不出来了。
在接下来的几十年里,所有这些推测都被证明是正确的。
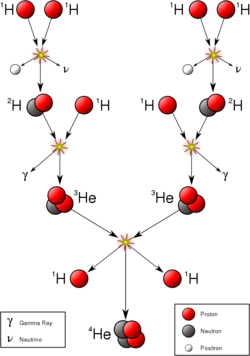
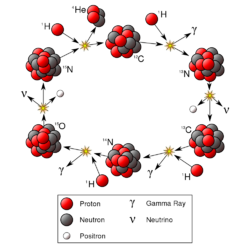
太阳能量和类似大小的恒星的主要来源是氢聚变形成氦(质子-质子链反应),它发生在 1400 万 K 的太阳核心温度下。最终的结果是四个质子融合成一个粒子,释放出两个正电子和两个中微子(其中两个质子变成中子)和能量。在较重的恒星中,碳氮氧循环和其他过程更重要。当恒星耗尽大部分氢时,它开始合成更重的元素。这种聚变发生在质量更大的恒星在生命结束时经历一颗猛烈的超新星,这个过程被称为超新星核合成。
3. 聚变发生的条件
在发生聚变之前,必须克服静电力的巨大能量障碍。在很远的距离,两个裸露的原子核互相排斥,因为它们带正电荷的质子之间有排斥力。然而,如果两个原子核能靠得足够近,静电斥力就能被量子效应克服,在量子效应中,原子核可以通过库仑力穿隧。
当一个核子(如质子或中子)被加到原子核上时,核力会把它吸引到原子核的所有其他核子上(如果原子足够小的话),但主要是吸引到它的近邻上,因为核力的作用范围很短。原子核内部的核子比表面的核子有更多的相邻核子。由于较小的原子核具有较大的表面积体积比,因此核力作用下的每核子结合能一般随原子核的大小而增大,但趋近于与直径约为 4 个核子的原子核的结合能的极限值。重要的是要记住核子是量子物体。例如,由于原子核中的两个中子彼此相同,区分两个中子的目标,例如哪个在内部,哪个在表面,实际上是没有意义的,因此包含量子力学对于正确的计算是必要的。
另一方面,静电力是一个平方反比力,所以加入原子核的质子会感受到原子核中所有其他质子的静电斥力。由于静电力,每个核子的静电能随原子核原子数的增加而无限制地增加。
作用效果相反的静电力和强核力最终效果是使每个核子的结合能通常随着尺寸的增加而增加,直到元素铁和镍,然后随原子核的数量增加而减少。最终,结合能变成负的,非常重的原子核(都有超过 208 个核子,相当于直径约为 6 个核子)是不稳定的。四个结合最紧密的原子核,按每个核子的结合能递减顺序是 $^{62}Ni,^{58}Fe,^{56}Fe,$ 和 $^{60}Ni$。[8]镍同位素,$^{62}Ni$ 较稳定,铁同位素 $^{56}Fe$ 更常见。这是因为恒星没有简单的方法来产生 $^{62}Ni$,只有通过通过 $\alpha$ 反应过程。
这一普遍趋势的一个例外是氦-4 原子核,它的结合能高于仅次于它的最重元素锂。这是因为质子和中子是费米子,根据泡利不相容原理,它们不可能以完全相同的状态存在于同一个原子核中。原子核中每个质子或中子的能态都能同时容纳一个自旋向上的粒子和一个自旋向下的粒子。氦-4 具有异常大的结合能,因为它的原子核由两个质子和两个中子组成,所以它的四个核子都处于基态。任何额外的核子都会进入高能态。事实上,氦-4 原子核是如此紧密地结合在一起,以至于在核物理中它通常被视为一个单一的量子力学粒子,即 $\alpha$ 粒子。
如果把两个原子核结合在一起,情况也是类似的。当它们相互靠近时,一个原子核中的所有质子排斥另一个原子核中的所有质子。直到两个原子核足够长时间地靠近,强核力才会(通过隧穿)取代排斥性静电力。因此,即使最后的能量状态较低,也有一个必须首先克服的巨大能量障碍。它叫做库仑势垒。
对于氢的同位素来说,库仑势垒是最小的,因为它们的原子核只含有一个正电荷。双质子是不稳定的,所以中子也必须参与其中,理想情况下,氦原子核与它的结合非常紧密,是产物之一。
使用氘氚燃料,产生的能量势垒约为 0.1 兆电子伏。相比之下,从氢中移除一个电子所需的能量是 13.6 eV,大约是所需能量的 7500 倍。聚变的(中间)结果是一个不稳定的 $^{5}He$ 原子核,它立即射出一个 14.1 MeV 的中子。剩余 $^{4}He$ 核的反冲能为 3.5 MeV,释放的总能量为 17.6 MeV。这比克服能量障碍所需的能量要多很多倍。
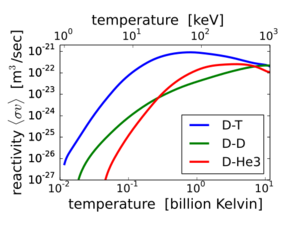
反应截面 $\sigma$是聚变反应概率的一种量度,是两个反应物原子核相对速度的函数。如果反应物具有速度分布,例如热分布,那么对横截面积和速度的分布进行平均是有效的。这个平均值被称为 “反应性”,表示为 $<\sigma v >$。反应速率(每次每体积的聚变)为 $<\sigma v >$ 乘以反应物数量密度的乘积: $$f=n_1n_2<\sigma v>~$$ 如果一种原子核与自身一样的原子核反应,例如 DD 反应,那么产物 $n_1n_2$ 必须替换为 $(1/2)n^2$。
$<\sigma v >$ 从室温下的几乎为零增加到温度为 10 – 100 keV 时的有意义幅度数值。在这些温度下,聚变反应物以等离子态存在,远远高于典型的电离能(氢的电离能为 13.6 eV)。
$<\sigma v >$ 通过考虑劳森准则,可以得到具有特定能量的器件中温度的函数限制时间。这是一个极具挑战性的障碍,需要在地球上克服,这就解释了为什么核聚变研究花了许多年才达到目前的先进技术水平。[9]
4. 实现聚变的方法
4.1 热核聚变
如果物质被充分加热(因此成为等离子体)并受到限制,则由于粒子的极端热动能的碰撞,可能会发生聚变反应。热核武器产生的核聚变能量是无法控制的。受控热核融合的概念是利用磁场来限制等离子体。
4.2 惯性约束核聚变
惯性约束聚变(ICF)是一种旨在通过加热和压缩燃料靶(通常是含有氘和氚的小球)来释放聚变能的方法。
4.3 惯性静电约束
惯性静电约束是一套利用电场将离子加热到熔融状态的设备。最著名的是《fusor 》。从 1999 年开始,许多业余爱好者已经能够使用这些自制的设备进行业余的核聚变。[10][11][12][13]其他 IEC 设备包括:Polywell,MIX POPS[14]和 “大理石” 概念。[15]
4.4 波束-波束或波束-目标融合
如果引发反应的能量来自于加速原子核中的一个,这个过程称为波束-目标融合;如果两个原子核都被加速,那就是波束-波束融合。
基于加速器的光离子融合是一种利用粒子加速器获得足够的粒子动能来引发光离子融合反应的技术。加速光离子是相对容易的,并且可以在一个有效的方式中完成——只需要一个真空管,一对电极,和一个高压变压器;在两个电极之间用 10kv 的电压就可以观察到融合。基于加速器的聚变(通常是冷目标)的关键问题是聚变截面比库仑相互作用截面低许多个数量级。因此,绝大多数离子消耗它们的能量来发射轫致辐射和靶原子的电离。被称为密封管中子发生器的装置与这一讨论特别相关。这些小型设备是填充有氘和氚气体的微型粒子加速器,其排列方式允许这些原子核的离子相对于氢化物靶加速,氢化物靶中也包含氘和氚,在这里发生聚变,释放出中子通量。每年全球生产数百台中子发生器,供石油工业使用,并用于测量设备,以确定和绘制石油储量。
为了克服束-靶融合中的轫致辐射问题,$3 \alpha$ 太阳能源公司提出了一种组合方法,该方法基于两个方向相反的等离子体团的相互渗透。[16]理论工作表明,通过创建和加热两个加速的迎面碰撞的等离子体团,使其能达到几千电子伏的热能,这与热核聚变所需的热能相比是低的,即使使用像 P-11B 这样的电子燃料,也可以获得净聚变增益。为了通过这种方法达到盈亏平衡的必要条件,加速等离子体必须有足够的碰撞速度,根据聚变燃料的种类,其速度大约为每秒几千公里(10^6 米/秒)。此外,等离子体密度必须介于惯性和磁融合标准之间。
4.5 介子催化核聚变
介子催化聚变是在常温下发生的聚变过程。史蒂文·琼斯在 20 世纪 80 年代初对此进行了详细研究。由于产生μ子所需的高能量,该反应产生的净能量并不成功,μ子的短值为 2.2 s 半衰期,μ子很有可能结合到新的α粒子,从而停止催化融合。[17]
4.6 其他理论
科学界还研究了一些其他约束原理。
- 反物质初始化聚变使用少量的反物质来触发微小的聚变爆炸。这主要是在使核脉冲推进和纯聚变炸弹可行的背景下进行研究的。由于仅制造反物质的成本就很高昂,它还远未成为一种实用的能源。
- 2005 年 4 月,加州大学洛杉矶分校的一个团队报道了热电聚变。科学家们使用了焦热电的晶体从 34°加热到 7° c(29 至 45 f),与钨针结合产生了约 25GV/m 的电场,使氘原子核电离并加速成为氘化铒靶。在估计的能量水平下,[18]在估计的能量水平下,可能发生 D-D 聚变反应,产生氦-3 和一个 2.45 MeV 的中子。虽然它是一种有效的中子发生器,但由于它所需要的能量远远超过它所产生的能量,所以它并不用于发电。[19][20][21][22]
- 混合核聚变-裂变(混合核电)是一种利用核聚变和裂变过程相结合来发电的方法。这个概念可以追溯到 20 世纪 50 年代,并在 20 世纪 70 年代由汉斯·贝特(Hans Bethe)短暂地提出,但由于在实现纯核聚变方面的延迟,直到 2009 年才重新引起人们的兴趣。[23]
- 20 世纪 70 年代中期在洛斯阿拉莫斯国家实验室(LANL)进行的 PACER 项目探索了核聚变动力系统的可能性,该系统包括在地下空洞中引爆小型氢弹(核聚变炸弹)。作为一种能源,该系统是唯一可以证明使用现有技术工作的聚变电力系统。然而,这也需要大量的、持续的核弹供应,这使得这样一个系统的经济学相当有问题。
- 气泡核聚变 (被揭露出造假)也被称为声融合,是通过声空化实现融合的一种 “机制”,它在 21 世纪初受到了重视。但随后的复制尝试失败,首席研究员 Rusi Taleyarkhan 在 2008 年被判犯有研究不端行为[24]
5. 重要反应
5.1 天体物理反应链
在恒星核心的温度和密度下,聚变反应的速率很慢。例如,在太阳核心温度($T\approx15 MK$)和密度($160 g/cm^3$),能量释放率仅为 $276 \mu W/cm^3$——大约是静止人体产生热量的体积率的四分之一。[25]因此,在实验室里复制用于核聚变发电的恒星核心条件是完全不切实际的。因为核反应速率取决于密度和温度,并且大多数聚变方案在相对较低的密度下运行,所以这些方法强烈依赖于较高的温度。聚变速率作为温度的函数($expE/kT$)),这就要求地面反应堆的温度要比恒星内部的温度高 10-100 倍:$T\approx0.1-1.0\times10^9K$.
5.2 地面反应的标准和候选
在人工聚变中,主要燃料不限于质子,可以使用更高的温度,因此选择具有更大横截面的反应。另一个问题是中子的产生,它可以从放射学上激活反应堆结构,但也有优点,可以从体积上提取聚变能并产生氚。不释放中子的反应称为非中子反应。
要使聚变成为有用的能源,必须满足几个标准。它必须:
是放热的 这将反应物限制在最低限度 Z 结合能曲线的(质子数)侧。它也制造氦 4 He 最常见的产品是因为它的粘合力特别强,尽管 3 He 和 3 T 也出现了。 涉及低原子序数( Z)原子核 这是因为在原子核离得足够近从而发生聚变之前,必须克服静电斥力,而这种斥力与原子核所含的质子数(原子序数)直接相关。 有两种反应物 在任何低于恒星密度的情况下,三体碰撞都不可能发生。在惯性约束中,恒星密度和温度都被超过,以补偿劳森准则第三个参数的缺点,即惯性约束聚变的限制时间非常短。 有两种或两种以上的产物 这允许能量和动量同时守恒,而不依赖于电磁力。 保存质子和中子 弱相互作用的横截面太小。 很少有反应符合这些标准。以下是具有最大横截面的那些:[26]
| (1) | $^{2}$ $_{1}D$ | + | $^{3}$ $_{1}T$ | → | $^{4}$ $_{2}He$ | ( | 3.5 MeV | ) | + | $n^0$ | ( | 14.1 MeV | ) | |
| (2i) | $^{2}$ $_{1}D$ | + | $^{2}$ $_{1}D$ | → | $^{3}$ $_{1}T$ | ( | 1.01 MeV | ) | + | $p^+$ | ( | 3.02 MeV | ) | $50\%$ |
| (2ii) | → | $ ^{3}$ $_{2}He $ | ( | 0.82 MeV | ) | + | $n^0$ | ( | 2.45 MeV | ) | $50\%$ | |||
| (3) | $^{2}$ $_{1}D$ | + | $^{3}$ $_{2}He$ | → | $^{4}$ $_{2}He$ | ( | 3.6 MeV | ) | + | $p^+$ | ( | 14.7 MeV | ) | |
| (4) | $^{3}$ $_{1}T$ | + | $^{3}$ $_{1}T$ | → | $^{4}$ $_{2}He$ | + | 2 | $n^0$ | + | 11.3 MeV | ||||
| (5) | $^{3}$ $_{2}He$ | + | $^{3}$ $_{2}He$ | → | $^{4}$ $_{2}He$ | + | $2 p^+$ | + | 12.9 MeV | |||||
| (6i) | $^{3}$ $_{2}He$ | + | $^{3}$ $_{1}T$ | → | $^{4}$ $_{2}He$ | + | $p^+$ | + | $n^0$ | + | 12.1 MeV | $57\%$ | ||
| (6ii) | → | $^{4}$ $_{2}He$ | ( | 4.8 MeV | ) | + | $^{2}$ $_{1}D$ | ( | 9.5 MeV | ) | $43\%$ | |||
| (7i) | $^{2}$ $_{1}D$ | + | $^{6}$ $_{3}Li$ | → | $2^{4}$ $_{2}He$ | + | 22.4 MeV | |||||||
| (7ii) | → | $^{3}$ $_{2}He$ | + | $^{4}$ $_{2}He$ | + | $n^0$ | + | 2.56 MeV | ||||||
| (7iii) | → | $^{7}$ $_{3}Li$ | + | $p^+$ | + | 5.0 MeV | ||||||||
| (7iv) | → | $^{7}$ $_{4}Be$ | + | $n^0$ | + | 3.4 MeV | ||||||||
| (8) | $p^+$ | + | $^{6}$ $_{3}Li$ | → | $^{4}$ $_{2}He$ | ( | 1.7 MeV | ) | + | $^{3}$ $_{2}He$ | ( | 2.3 MeV | ) | |
| (9) | $^{3}$ $_{2}He$ | + | $^{6}$ $_{3}Li$ | → | $2^{4}$ $_{2}He$ | + | p+ | + | 16.9 MeV | |||||
| (10) | $p^+$ | + | $^{11}$ $_{5}B$ | → | $3^{4}$ $_{2}He$ | + | 8.7 MeV |
对于两种产物的反应,能量与它们的质量成反比,如图所示。在大多数有三种产物的反应中,能量的分布是不同的。对于能产生一组以上产物的反应,给出了它们的分支比。
有些候选反应可以立即消除。$D^{-6}Li$ 反应相比没有优势 $p^{+}-^{11}$ $_{5}B$ 因为它基本上很难燃烧,但会通过 $^{2}$ $_1D$-$^{2}$ $_1D$ 副反应产生更多的中子。还有一个 $p^{+}-^{7}$ $_{3}Li$ 反应,但是横截面太低,除非可能在 $T_i> 1 MeV$,但在如此高的温度下,吸热的直接产生中子的反应也变得非常重要。最后还有一个 $p^{+}-^{9}$ $_{4}Be$ 反应,这不仅难以燃烧,而且 $^{9}$ $_{4}Be$ 很容易被诱导分裂成两个 $\alpha$ 粒子和一个中子。
除了聚变反应之外,为了在 “干式” 聚变弹和一些提议的聚变反应堆中 “繁殖” 氚,以下与中子的反应也很重要:
1954 年,美国进行 “喝彩城堡” 聚变炸弹试验时,这两个方程中的后一个是未知的。作为迄今为止测试过的第二颗核聚变炸弹(也是第一颗使用锂的核聚变炸弹),“喝彩城堡” 的 “虾” 号的设计者明白 $^6Lii$ 在氚生产中的作用,但未能认识到 $^7Li$ 裂变将大大提高炸弹的产量。$^7Li$ 中子截面小,中子能量低,但在 5Mev 以上的截面较高。[27]1500 万吨的产量比预计的 600 万吨高 150%,并导致了意外的辐射。
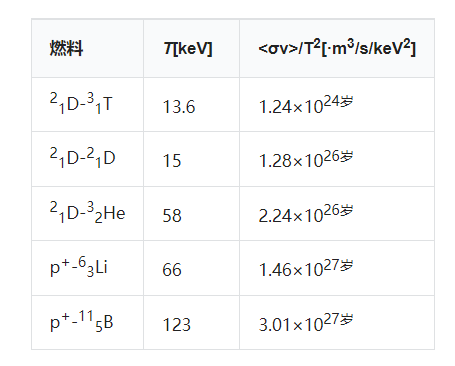
而一个经济的装置总是在这个最大压力附近运行。鉴于这种压力,获得最大的融合输出温度时选择这<σv > / T2 是一个最大值。这也是温度的价值三重积 nTτ点火所需最低,因为这要求值成反比<σv > / T2(见劳森判据)。(如果聚变反应产生的能量足够维持温度而不需要外部加热,等离子体就会被 “点燃”。)该最佳温度和<σv>/T 的值 2 下表给出了其中一些反应的温度。
请注意,许多反应形成链。例如,一个反应堆 $^{3}$ $_{1}T$ 和 $^{3}$ $_{2}He$ 产生一些 $^{2}$ $_{1}D$,这样就可以在 $^{2}$ $_{1}D$-$^{3}$ $_{2}He$ 能量 “正确” 时的反应。一个巧妙的想法是将反应(8)和(9)结合起来。$^{3}$ $_{2}He$ 从反应(8)可以与 $^{6}$ $_{3}Li$ 在完全热化之前在反应(9)中反应。这产生了一个高能质子,它反过来在热化之前经历反应(8)。但是详细分析表明,这种想法不能很好地发挥作用。因此这是一个很好的说明通常假设的麦克斯韦等离子体是不合适的例子。
5.3 中子性、限制要求和功率密度
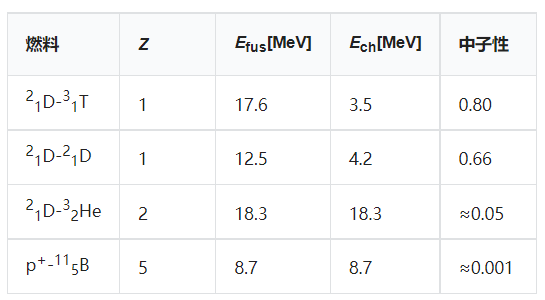
上述任何反应原则上都可以作为聚变发电的基础。除了上面讨论的温度和截面,我们还必须考虑聚变产物的总能量 Efus,带电聚变产物的能量 $E_ch$,和原子序数为 Z 的非氢反应物。
$^{2}$ $_{1}D$-$^{2}$ $_{1}D$ 这种反应会带来一些困难。首先,必须对两个分支(2i)和(2i)进行平均。更困难的是决定如何处理 $^{3}$ $_{1}T$ 和 $^{3}$ $_{2}He$ 产物。$^{3}$ $_{1}T$ 氘等离子体燃烧的非常好,几乎不可能从等离子体中提取。21D-32He 更高的温度下反应进行优化,使燃耗达到最优,$^{2}$ $_{1}D$-$^{2}$ $_{1}D$ 温度可能很低。因此,假设 $^{3}$ $_{1}T$ 但不是 $^{3}$ $_{2}He$ 被烧掉并把它的能量加到净反应中,这意味着总反应是(2i)、(2i)和(1)的和:
$$^{5}_{2}\text{D} \rightarrow ^{4}_{2}\text{He} + 2n^{0} + ^{3}_{2}\text{He} + p^{+}, \quad E_{\text{fus}} = 4.03 + 17.6 + 3.27 = 24.9 \, \text{MeV}, \quad E_{\text{ch}} = 4.03 + 3.5 + 0.82 = 8.35 \, \text{MeV}.~$$
为了计算反应堆的功率(其中反应速率由 D-D 步骤决定),我们计算 $^{2}$ $_{1}D$-$^{2}$ $_{1}D$ 聚变能每个 D-D 反应,如 $\quad E_{\text{fus}}$= (4.03 MeV + 17.6 MeV)×50% + (3.27 MeV)×50% = 12.5 MeV,带电粒子的能量为 $\quad E_{\text{ch}}$= (4.03 MeV + 3.5 MeV)×50% + (0.82 MeV)×50% = 4.2 MeV。(注:如果氚离子与氘核反应时仍有很大的动能,那么产生的氦-4 的动能可能与 3.5Mev 差别很大。[28]所以对带电粒子能量的计算只是近似平均值。)每氘核消耗的能量是这个的 2/5,即 5.0 MeV (每千克氘的比能量约为 2.25 亿 MJ)。
另一个独特的方面是 $^{2}$ $_{1}D$-$^{2}$ $_{1}D$ 反应是只有一种反应物,在计算反应速率时必须考虑。
有了这个选择,我们将四个最重要反应的参数制成表格
最后一列是反应的中子性,即以中子形式释放的聚变能量的比例。这是一个重要的指标,与中子相关的问题,如辐射损伤、生物屏蔽、远程操作和安全的重要性。对于前两个反应,计算如下(Efus-Ech)/Efus。对于最后两个反应,计算结果为零,引用的值是基于热平衡状态下等离子体中产生中子的副反应的粗略估计。
当然,反应物也应该以最佳比例混合。这种情况下,每个反应物离子加上它的电子占了一半的压强,假设总压强是固定的,这意味着非氢离子的粒子密度比氢离子的粒子密度小 2/(Z+1)。因此,除了<σv>/T 值的任何差异之外,这些反应的速率降低了相同的因子。另一方面,因为 $^{2}$ $_{1}D$-$^{2}$ $_{1}D$ 反应只有一种反应物,其反应速率是燃料在两种不同的含氢物质之间分配时的两倍,从而产生了更有效的反应。
因此,由于非氢燃料需要更多的电子,而这些电子在没有参与聚变反应的情况下承担了压力,因此对 $(2/(Z+1))$ 非氢燃料有 $(2/(Z+1))$ 的 “惩罚”。(电子的温度几乎等于离子的温度,这通常是一个很好的假设。然而,一些作者讨论了电子比离子冷得多的可能性。在这种情况下,即所谓的 “热离子模式”,“惩罚” 将不适用。)同时还有一个因子 2 的 “奖励”。$^{2}$ $_{1}D$-$^{2}$ $_{1}D$ 因为每一种离子都可以与其他离子反应,而不仅仅是其中的一部分。
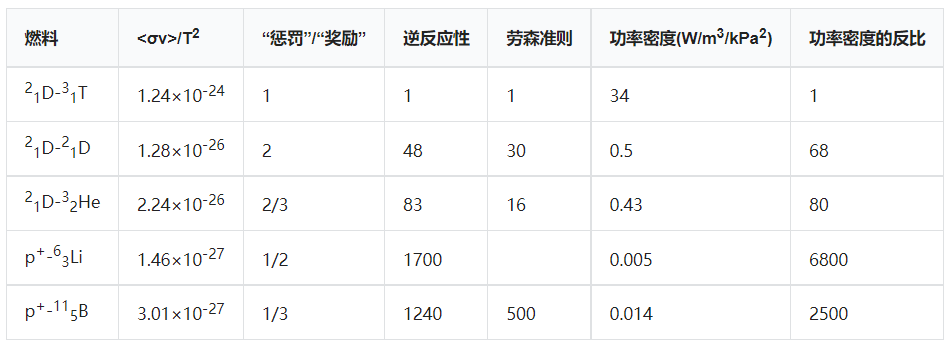
我们现在可以在下表中比较这些反应。
<σv>/T 的最大值取自上一张表。“惩罚”/“奖励” 因素是与非氢反应物或单一物质反应有关。“逆反应性” 一栏的值是用第二栏和第三栏的乘积除以 1.24 得到 $\times10^{-24}$ 得到的。它表明了其他反应比 $^{2}$ $_{1}D$-$^{3}$ $_{1}T$ 反应发生慢的因素。在可比条件下的反应。列 “劳森准则” 用以下公式对这些结果进行加权 $\quad E_{\text{ch}}$,并给出了一个指标,相对于上述两种反应的难度,这些反应的点火难度相对于 $^{2}$ $_{1}D$-$^{3}$ $_{1}T$ 反应要大很多。倒数第二列标有 “功率密度”,并通过 $\quad E_{\text{fus}}$ 对实际反应性进行加权,最后一栏显示了其他反应的聚变功率密度与 $^{2}$ $_{1}D$-$^{3}$ $_{1}T$ 反应相比低多少,这可以被认为是经济潜力的一种衡量。
5.4 准中性、各向同性等离子体中的轫致辐射损失
在许多系统中进行融合的离子基本上不会单独出现,而是会与电子总的来说中和了离子的体积电荷形成一个等离子体。电子的温度通常与离子的温度相当或更高,因此它们会与离子发生碰撞,并释放出 10-30 keV 能量的 x 射线辐射,这一过程被称为轫致辐射(Bremsstrahlung)。
太阳和恒星的巨大体积意味着在这个过程中产生的 x 射线不会逃逸,并将它们的能量储存回等离子体中。据说它们对 x 射线不透明。但是对于这种能量范围的 x 射线来说,任何陆地上的聚变反应堆都是光学厚度的。x 射线很难反射,但它们在不到毫米厚的不锈钢(反应堆防护层的一部分)中被有效吸收(并转化为热量)。这意味着轫致辐射过程将使能量从等离子体中被带走,使其冷却。
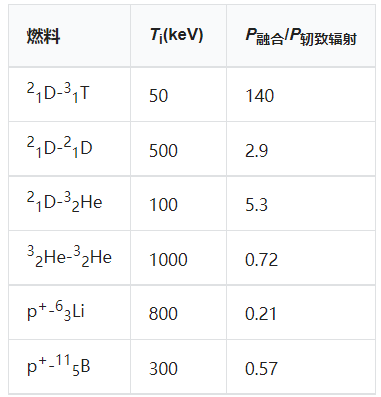
核聚变产生的能量与 x 射线辐射损失的比值是一个重要的品质因数。该比率通常在比最大功率密度高得多的温度下最大化(见前一小节)。下表显示了几种反应的最佳温度和该温度下的功率比的估计值:
聚变与轫致辐射功率的实际比值可能会因为几个原因而显著降低。首先,计算假设聚变产物的能量完全传输到燃料离子,然后燃料离子通过碰撞损失能量给电子,电子又通过轫致辐射损失能量然而,由于聚变产物的移动速度比燃料离子快得多,它们将把相当一部分能量直接提供给电子。其次,等离子体中的离子假设为纯燃料离子。在实际应用中,杂质离子的比例会很大,这就会降低比例。特别是,聚变产物本身必须留在等离子体中,直到它们释放出能量,并且在任何提出的限制方案中,都将在等离子体中保留一段时间。最后,除了轫致辐射外的所有能量损失通道都被忽略了。最后两个因素是相关的。在理论和实验的基础上,粒子和能量约束似乎是密切相关的。在一个能很好地保留能量的约束方案中,核聚变产物会逐渐形成。如果核聚变产物被有效地排出,那么能量约束也会很差。
与轫致辐射相比,使聚变功率最大化的温度在任何情况下都高于使功率密度最大化和使聚变三重积所需值最小化的温度。这不会改变的最佳操作点,$^{2}$ $_{1}D$-$^{3}$ $_{1}T$ 很大程度上是因为轫致辐射的比例很低,但它会将其他燃料推入功率密度相对于 $^{2}$ $_{1}D$-$^{3}$ $_{1}T$ 甚至更低,所需的限制甚至更难实现。$^{2}$ $_{1}D$-$^{2}$ $_{1}D$ 和 $^{3}$ $_{2}He$ 轫致辐射损失将是一个严重的,可能是令人望而却步的问题。$^{3}$ $_{2}He$-$^{3}$ $_{2}He$,$p^{+}-^{6}$ $_{3}Li$ 和 $p^{+}-^{11}$ $_{5}B$ 轫致辐射的损失似乎使使用这些燃料的聚变反应堆不可能产生准中性、各向同性的等离子体。2008 年,走出这一困境的一些方法被考虑——并被拒绝——在等离子体聚变系统的基本限制中没有热力学平衡。。[29][30]这一限制不适用于非中性和各向异性等离子体;然而,这些自身也会产生一些挑战需要应对。
6. 横截面的数学描述
6.1 经典物理下的
在经典的图像中,原子核可以被理解为通过库仑力相互排斥的硬球体,但是一旦两个球体足够接近接触就会融合。将原子核半径估计为 1fm 左右,两个氢原子聚变所需能量为: $$E_{\text{thresh}} = \frac{1}{4\pi \epsilon_0} \frac{Z_1 Z_2}{r} \xrightarrow{2 \, \text{protons}} \frac{1}{4\pi \epsilon_0} \frac{e^2}{1 \, \text{fm}} \approx 1.4 \, \text{MeV}~$$ 这意味着太阳核心的玻尔兹曼分布温度约为 1.4 keV,氢达到阈值的概率为 $10^{-290}$ 也就是说,永远不会发生聚变。然而,由于量子力学,太阳的核聚变确实发生了。
6.2 截面参数化
与经典图像相比,融合发生的概率大大增加,这是由于有效半径得拖尾效应为德布罗意波长也量子隧道穿过潜在的障碍。为了确定聚变反应的速率,最值得重视的值是横截面,它通过给出相互作用的特征区域来描述粒子融合的概率。聚变横截面积的估计通常分为三部分: $$\sigma \approx \sigma_{\text{geometry}} \times T \times R~$$
$\sigma_{\text{geometry}}$ 表示几何横截面, T 表示屏障的透明度, R 表示反应的反应特征。
$\sigma_{\text{geometry}}$ 大约是德布罗意波长的平方, $\sigma_{\text{geometry}} \approx \lambda^2 = \left( \frac{\hbar^2}{m_r v} \right)^2 \propto \frac{1}{\epsilon}, m_r$ 表示系统的约化质量 $\epsilon$ 是系统的质量能量中心。
T 可以用伽莫夫透明度近似, 形式为: $T \approx e^{-\sqrt{\epsilon_G / \epsilon}}$, $\epsilon_G = \left( \pi \alpha Z_1 Z_2 \right)^2 \times 2 m_r c^2$ 表示伽莫夫因子, 来自对穿过井势垒的量子隧穿概率的估计。
R 包含特定反应的所有核物理, 并根据相互作用的特性得出非常不同的值。然而, 对于大多数反应来说 $R(\epsilon)$ 与伽莫夫因子的变化相比很小, 因此可以用一个简单做无维物理因子的函数来近似。$S(\epsilon)$ 能量变化很小。综合这些相关性质, 横截面作为能量函数的一个近似形式为: $$\sigma(\epsilon) \approx \frac{S(\epsilon)}{\epsilon} e^{-\sqrt{\epsilon_G / \epsilon}}~$$ 更详细的横截面形式可以通过基于核物理的模型和 $R$ 矩阵理论得到。
6.3 聚变截面公式
海军研究实验室的等离子体物理公式集[31]给出了粒子入射到目标离子的能量(单位为 keV)的总横截面: $$\sigma_{\text{NRL}}(\epsilon) = \frac{A_5 + \left( \left( A_4 - A_3 \epsilon \right)^2 + 1 \right)^{-1} A_2}{\epsilon \left( e^{A_1 \epsilon^{-1/2}} - 1 \right)}~$$具有以下数值:
| DT(1) | DD(2i) | DD(2i) | DHe^3(3) | TT(4) | 这 $^3$(6) | |
| A1 | 45.95 | 46.097 | 47.88 | 89.27 | 38.39 | 123.1 |
| A2 | 50200 | 372 | 482 | 25900 | 448 | 11250 |
| A3 | 1.368e-2 | 4.36e-4 | 3.08e-4 | 3.98e-3 | 1.02e-3 | 0 |
| A4 | 1.076 | 1.22 | 1.177 | 1.297 | 2.09 | 0 |
| A5 | 409 | 0 | 0 | 647 | 0 | 0 |
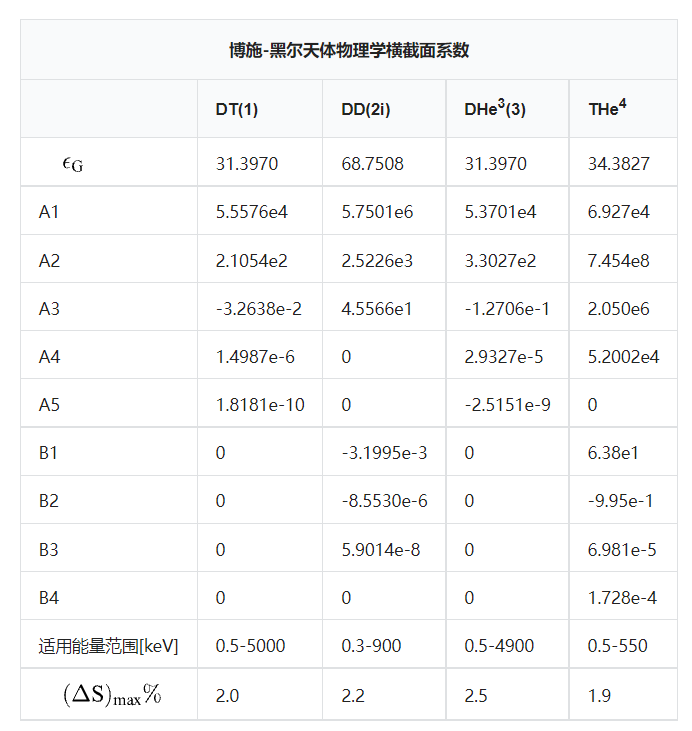
$$S_{\text{Bosch-Hale}}(\epsilon) = \frac{A_1 + \epsilon \left( A_2 + \epsilon \left( A_3 + \epsilon \left( A_4 + \epsilon A_5 \right) \right) \right )}{1 + \epsilon \left( B_1 + \epsilon \left( B_2 + \epsilon \left( B_3 + \epsilon B_4 \right) \right) \right)},\text{具有系数值:}~$$
7. 参考文献
[1] ^物理弹性书 Archived 28 12 月 2011 at the Wayback Machine。Ck12.org。检索于 2012 年 12 月 19 日。.
[2] ^Bethe, Hans A. (April 1950). "The Hydrogen Bomb". Bulletin of the Atomic Scientists. 6 (4): 99–104, 125–..
[3] ^"ITER – the way to new energy". ITER. 2014. Archived from the original on 22 September 2012..
[4] ^Moses, E. I. (2009). "The National Ignition Facility: Ushering in a new age for high energy density science". Physics of Plasmas. 16 (4): 041006. Bibcode:2009PhPl...16d1006M. doi:10.1063/1.3116505..
[5] ^Kramer, David (March 2011). "DOE looks again at inertial fusion as potential clean-energy source". Physics Today. 64 (3): 26–28. Bibcode:2011PhT....64c..26K. doi:10.1063/1.3563814..
[6] ^Eddington, A. S. (October 1920). "The Internal Constitution of the Stars". The Scientific Monthly. 11 (4): 297-303. JSTOR 6491..
[7] ^Eddington, A. S. (1916). "On the radiative equilibrium of the stars". Monthly Notices of the Royal Astronomical Society. 77: 16–35. Bibcode:1916MNRAS..77...16E. doi:10.1093/mnras/77.1.16..
[8] ^最紧密结合的原子核。Hyperphysics.phy-astr.gsu.edu。检索于 2011-08-17。.
[9] ^什么是劳森标准,或者如何使聚变能可行.
[10] ^"Fusor Forums • Index page". Fusor.net. Retrieved 2014-08-24..
[11] ^"Build a Nuclear Fusion Reactor? No Problem". Clhsonline.net. 23 March 2012. Archived from the original on 30 October 2014. Retrieved 24 August 2014..
[12] ^"Extreme DIY: Building a homemade nuclear reactor in NYC". BBC News. Retrieved 30 October 2014..
[13] ^Schechner, Sam (2008-08-18). "Nuclear Ambitions: Amateur Scientists Get a Reaction From Fusion – WSJ". Online.wsj.com. Retrieved 2014-08-24..
[14] ^Park J, Nebel RA, Stange S, Murali SK (2005). "Experimental Observation of a Periodically Oscillating Plasma Sphere in a Gridded Inertial Electrostatic Confinement Device". Phys Rev Lett. 95 (1): 015003. Bibcode:2005PhRvL..95a5003P. doi:10.1103/PhysRevLett.95.015003. PMID 16090625..
[15] ^“多重双极循环光束线实验” 海报演示,2011 年美日 IEC 会议,亚历克斯·克莱因博士.
[16] ^J.Slough,G. Votroubek 和 C. Pihl,“通过合并和压缩超音速场反转构型等离子体团创造高温等离子体” Nucl。Fusion 51,053,008 (2011)。.
[17] ^Jones, S.E. (1986). "Muon-Catalysed Fusion Revisited". Nature. 321 (6066): 127–133. Bibcode:1986Natur.321..127J. doi:10.1038/321127a0..
[18] ^“热释电晶体驱动的核聚变观测” 的补充方法 “”。主要文章 Naranjo, B.; Gimzewski, J.K.; Putterman, S. (2005). "Observation of nuclear fusion driven by a pyroelectric crystal". Nature. 434 (7037): 1115–1117. Bibcode:2005Natur.434.1115N. doi:10.1038/nature03575. PMID 15858570..
[19] ^加州大学洛杉矶分校晶体聚变。Rodan.physics.ucla.edu。检索于 2011-08-17。Archived 8 6 月 2015 at the Wayback Machine.
[20] ^Schewe, Phil & Stein, Ben (2005). "Pyrofusion: A Room-Temperature, Palm-Sized Nuclear Fusion Device". Physics News Update. 729 (1). Archived from the original on 12 November 2013..
[21] ^走出寒冷:核聚变,真的。。Christiansciencemonitor.com(2005-06-06)。检索于 2011-08-17。.
[22] ^桌面上的核聚变...真的吗?。MSNBC (2005-04-27)。检索于 2011-08-17。.
[23] ^Gerstner, E. (2009). "Nuclear energy: The hybrid returns". Nature. 460 (7251): 25–8. doi:10.1038/460025a. PMID 19571861..
[24] ^Maugh II, Thomas. "Physicist is found guilty of misconduct". Los Angeles Times. Retrieved 17 April 2019..
[25] ^融合|融合教育。Fusedweb.pppl.gov(1998-11-09)。检索于 2011-08-17。[失效连结].
[26] ^M. Kikuchi, K. Lackner & M. Q. Tran (2012). Fusion Physics. International Atomic Energy Agency. p. 22. ISBN 9789201304100..
[27] ^第 4.7.4c 小节。Kayelaby.npl.co.uk。检索于 2012 年 12 月 19 日。.
[28] ^动量和能量平衡表明,如果氚的能量为 ET(中子、氚和氦的相对质量分别为 1、3 和 4),那么氦的能量可以是来自[(12ET)1/2(5×17.6MeV+2×ET)1/2]2/25 至[(12ET)1/2+(5×17.6MeV+2×ET)1/2]2/25。对于 ET=1.01 MeV 这给出的范围是 1.44 MeV 至 6.73 MeV。.
[29] ^Rider, Todd Harrison (1995). "Fundamental Limitations on Plasma Fusion Systems not in Thermodynamic Equilibrium". Dissertation Abstracts International. 56-07 (Section B): 3820. Bibcode:1995PhDT........45R..
[30] ^诺曼·罗斯托克;Binderbauer,Michl 和 Qerushi,阿尔坦。对不处于热力学平衡的等离子体聚变系统的基本限制。。fusion.ps.uci.edu.
[31] ^Huba, J. (2003). "NRL PLASMA FORMULARY" (PDF). MIT Catalog. Retrieved 11 November 2018..
[32] ^Bosch, H. S (1993). "Improved formulas for fusion cross-sections and thermal reactivities". IOP Science. Retrieved 22 November 2018..