贡献者: 白玫瑰
几何光学是以实验定律为基础发展出来的理论。历史上,人们通过实验观察光的传播路径,总结形成了多个实验定律,如光的直线传播定律、光的独立传播定律、折射定律和反射定律、费马原理与马吕斯定理。
1. 光的直线传播定律
在各向同性的均匀介质中,光沿直线传播,这就是光的直线传播定律。在日常生活中,各种障碍物大小、各种孔径尺寸远远比光的波长大得多,衍射现象极不明显,可以忽略不计,可以简单应用光的直线传播来分析宏观光现象,如影子的形成等。
2. 光的独立传播定律
从不同光源发出的光线,以不同方向经过介质某点,各光线互不影响,这就是光的独立传播定律。利用这条定律,可以让我们对光线传播规律的研究大大简化,即只需要关心某一研究对象光线的传播,而不考虑其他光线。注意,这条定律依然只用于分析宏观光现象,详见光的干涉相关内容。
3. 光的折射定律和反射定律
内容介绍
光在传播过程中遇到两种不同介质构成的界面时,在界面上会部分反射,部分折射。光的反射定律和折射定律描述了反射与折射前后光传播方向的不同。
历史上,光的反射定律和折射定律首先由实验得到,后来,人们通过电磁学理论进行了严格推导,也得出了它们(详见波动光学部分)。
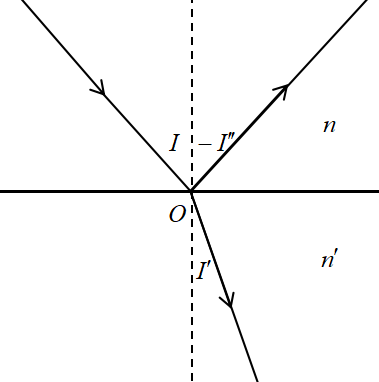
图 1:反射和折射定律
图 1 中,界面两侧介质折射率分别为 $n$ 和 $n'$。入射光线在界面入射点为 $O$,虚线为过 $O$ 点的法线,我们将入射光线和法线所在的平面称为入射面,则反射光线和折射光线均在入射面内(证明见波动光学内容,在此不证)。三条光线的传播方向可以使用它们与法线的夹角来描述。如图,我们将入射光线、折射光线和反射光线与法线夹角规定为 $I$、$I'$、$I''$。进一步地,将光线沿锐角转向法线,如果为顺时针,则夹角为正,反之,夹角为负。
此时,我们可以将折射定律表示为:
\begin{equation}
nsin(I)=n'sin(I') ~.
\end{equation}
将反射定律表示为:
\begin{equation}
I=-I'' ~.
\end{equation}
观察 $(1)$ 式,我们可以看出,令 $n'=-n$,即得 $I=-I''$,即 $(2)$ 式。这表明,反射定律是折射定律的特殊情况,可以使用统一的方法来研究折射光学现象与反射光学现象。
再观察 $(1)$ 式与 $(2)$ 式,我们完全可以将它们写成:
\begin{equation}
n'sin(I')=nsin(I) ~.
\end{equation}
\begin{equation}
-I''=I ~.
\end{equation}
这意味着,光线沿着折射光线出射的反方向入射经过界面折射后,沿原来入射光线的反方向出射,对于反射光线也是如此。这就是所谓的光路可逆。
矢量形式
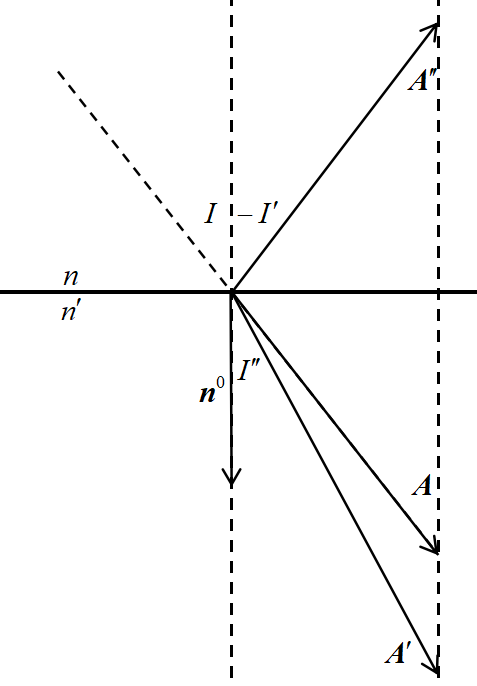
重新考察图 1 的光路传播,定义三个矢量 $ \boldsymbol{\mathbf{A}} $、$ \boldsymbol{\mathbf{A}} '$ 和 $ \boldsymbol{\mathbf{A}} ''$ 与法向单位矢量 $ \boldsymbol{\mathbf{n}} ^0$:
\begin{equation}
\begin{aligned}
& \left| \boldsymbol{\mathbf{A}} \right| = \left| \boldsymbol{\mathbf{A}} '' \right| = n ~, \\
& \left| \boldsymbol{\mathbf{A}} ' \right| = n' ~.
\end{aligned}
\end{equation}
它们的方向分别沿着入射光线、折射光线和反射光线的传播方向。
图 2:反射和折射定律矢量关系
由于三线共面,我们有:
\begin{equation}
\begin{aligned}
& \boldsymbol{\mathbf{A}} ' - \boldsymbol{\mathbf{A}} = \Gamma _ t \boldsymbol{\mathbf{n}} ^0 ~, \\
& \boldsymbol{\mathbf{A}} '' - \boldsymbol{\mathbf{A}} = \Gamma _ r \boldsymbol{\mathbf{n}} ^0 ~.
\end{aligned}
\end{equation}
等式两边同时点乘 $ \boldsymbol{\mathbf{n}} ^0$:
\begin{equation}
\begin{aligned}
& \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} ' - \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} = \Gamma _ t ~, \\
& \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} '' - \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} = \Gamma _ r ~.
\end{aligned}
\end{equation}
而:
\begin{equation}
\begin{aligned}
& \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} = ncos(I) ~, \\
& \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} ' = n'cos(I') ~, \\
& \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} '' = -ncos(I'') ~.
\end{aligned}
\end{equation}
代入得:
\begin{equation}
\begin{aligned}
& \Gamma _ t = \sqrt{n'^2 - n^2 + ( \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} )^2} - \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} ~, \\
& \Gamma _ r = -2 \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} ~.
\end{aligned}
\end{equation}
所以 $ \boldsymbol{\mathbf{A}} '$ 和 $ \boldsymbol{\mathbf{A}} ''$ 用 $ \boldsymbol{\mathbf{A}} $ 表示为:
\begin{equation}
\begin{aligned}
& \boldsymbol{\mathbf{A}} ' = \boldsymbol{\mathbf{A}} + \Gamma _ t \boldsymbol{\mathbf{n}} ^0 = \boldsymbol{\mathbf{A}} + (\sqrt{n'^2 - n^2 + ( \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} )^2} - \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} ) \boldsymbol{\mathbf{n}} ^0 ~, \\
& \boldsymbol{\mathbf{A}} '' = \boldsymbol{\mathbf{A}} + \Gamma _ r \boldsymbol{\mathbf{n}} ^0 = \boldsymbol{\mathbf{A}} - 2( \boldsymbol{\mathbf{n}} ^0 \cdot \boldsymbol{\mathbf{A}} ) \boldsymbol{\mathbf{n}} ^0 ~.
\end{aligned}
\end{equation}
全反射
光从光密介质进入光疏介质时,在两种介质的界面上会出现所谓的全反射现象,即 $I'=0$,没有折射光,光线被界面完全反射的情形。
对于式 $(1)$,将 $I'=0$ 代入,则此时的入射角 $I$ 即为发生全反射的临界角 $\theta_c$:
\begin{equation}
\theta _c=I=arcsin(\frac{n'}{n}) ~.
\end{equation}
当入射角大于临界角时,光线会被界面完全反射。1
4. 费马原理
5. 马吕斯定理
马吕斯定理指出,垂直于入射波面的入射光线束,经过任意次反射和折射,出射光线束仍然垂直于出射波面,并且在入射波面和出射波面间的所有光路光程都相等。
通过电磁学理论分析,马吕斯定理是显而易见的:同一个光源发出的入射波面,经过反射和折射得到的出射波面,两者相位差是恒定的。波的行进带来相位差,于是光程也恒定。
1. ^ 实际上,光并没有被 “完全” 反射,在折射介质中极靠近入射点的地方依然存在着光场,详见波动光学衰逝波相关内容。