G 力

贡献者：待更新

　　（本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译）

图 1：在直线和水平飞行中，升力(L)等于飞机自身的重力(W)。在 60°倾斜转弯中，升力等于重力的两倍(L = 2W)，此时飞行员体验了 2g 和双倍的重力。飞行倾角越大，感受到的 g 力也越大

　　 $g$ 力描述为重力的等效，或者更常见的单位质量力的量度–典型加速度–一种对重量的感知力，1 克物体的 $g$ 力等于地球上重力加速度的常规值， $g$ 大约 $9.8 m / s^{2}$ [1]。由于重力加速度间接产生重力，任何 $g$ 力都可以被描述为 “单位质量的重力”。当一个物体的表面被另一个物体的表面推动而产生 $g$ 力时，这个推动的反作用力对物体质量的每一个单位产生等大反向的 $g$ 力。所涉及的力的类型是通过物体内部的机械应力传递的。重力加速度(除了某些电磁力的影响)是物体自由落体产生加速度的原因。[2][3]

　　物体受到的 $g$ 力是由作用在物体自由运动上的所有非重力和非电磁力的矢量和决定的。实际上，如上所述，这些是物体表面之间的接触力。这种力对物体造成应力和应变，因为它们必须从物体表面传递。由于这些应变，大的 $g$ 力可能对物体产生损坏。

　　即使 $g$ 力是用标准重力自由落体加速度的倍数来描述的，但重力单独作用不会产生 $g$ 力。因此，地球表面的标准重力只是间接产生 $g$ 力，这实际是对重力产生抵抗的一种机械力。正是这些机械力在质量上产生了 $g$ 力。例如，一个 1g 的力作用在位于地球表面的物体上， $g$ 力是由地面向上施加的机械力引起的，它克服重力阻止物体自由下落。来自地面向上的接触力确保静止在地球表面的物体相对于自由落体而进行加速运动。(自由落体是物体向地球中心自由下落时遵循的路径)。物体内部的应力来自于仅从与地面接触点传递而来的接触力。

　　物体在引力场中自由运动时有质量而不表现重力或重力较小的一种状态，此时物体以惯性轨迹进行运动而感觉不到重力，这种情况被称为零重力(意思是零 $g$ 力)。这一点可以通过电梯内自由降落到地球中心(在真空中)的 “零重力” 条件，或者(非常近似地)地球轨道航天器内的 “零重力” 条件来证明。这些都是没有重量感的坐标加速度(速度变化)的例子。没有重力(零重力)的体验，不管它是如何产生的，都等同于失重。

　　在没有引力场的情况下，或者在与引力场成直角的方向上，适当的加速度和坐标加速度是相同的，任何坐标加速度都必须由相应的 $g$ 力加速度产生。这里的一个例子是自由空间中的火箭，发动机产生简单的速度变化，并对火箭和乘客产生 $g$ 力。

1. 单位和测量

　　国际单位制中加速度的计量单位是米/秒 2。然而，为了区分自由落体的加速度和简单加速度(速度变化率)，单位 $g$ (或 $g$ )经常被使用。1g 是地球表面重力产生的每单位质量的力，是标准重力(符号: gn)，定义为 9.80665 米每秒的平方，[4] 或者等同地 9.80665 每千克质量的牛顿力。请注意单位定义不随位置变化—站在月球上的 $g$ 力约为 0.165g，即几乎是在地球上的 1/6。

　　单位 $g$ 不是国际单位制之一，国际单位制单位用 “ $g$ ” 表示克。此外，“ $g$ ” 不应与 “ $G$ ” 混淆，后者是重力常数的标准符号。[5] 这种符号通常用于航空，特别是在特技飞行或军用航空中，用来描述飞行员为了保持清醒而必须克服的增加的力，而不是重力诱发的意识丧失。[6]

　　 $g$ 力的测量通常使用加速度计来实现。在某些情况下， $g$ 力可以使用适当校准的天平进行测量。比力是 $g$ 力的另一个名称。

2. 加速度和力

　　 $g$ 力这个术语在技术上是不正确的，因为它是加速度而不是力的度量。加速度是一个矢量， $g$ 力加速度(简称 “g-forces”)通常表示为标量，正 $g$ 力指向下方(表示向上加速度)，负 $g$ 力指向上方。因此， $g$ 力是加速度的矢量。它是一种加速度，必须由机械力产生，不能由简单的引力产生。仅有重力作用的物体没有 $g$ 力，被称为是失重的。

　　 $g$ 力，当乘以它们作用的质量时，这个术语在某种与机械相关联的力上具有一定的意义，这个力产生压缩应力和拉伸应力。这种力产生了重力的感觉，但是由于向下方向上正重力的定义，等式带有符号变化，因此重力的方向与 $g$ 力加速度的方向相反:

　　重力=质量×（-g 力）（Weight = mass ×（-g-force））负号的原因是 $g$ 力在物体上产生的实际力(即测量的重量)与 $g$ 力的符号方向相反，因为在物理学中，重力不是产生加速度的力，而是与之等大反向的反作用力。如果向上的方向被认为是正的(正常的笛卡尔约定)，那幺正 $g$ 力(指向上方的加速度矢量)在任何质量上产生一个向下的力/重力(一个例子是火箭发射的正加速度，产生向下的重力)。同样，一个负 $g$ 力是指向下方加速度矢量(y 轴上的负方向)，这种向下的加速度在一个方向上产生向上重力 (从而将飞行员向上拉出座椅，并迫使血液流向正常方向的飞行员头部)。

　　如果 $g$ 力(加速度)垂直向上，由地面(通过时空加速)施加，或者由电梯地板施加给站立的人，那么大部分身体会受到压缩应力，在任何高度，如果乘以面积，该压缩应力就是相关的机械力，该机械力是 $g$ 力和支撑质量(支撑水平面以上的质量，包括从该水平面以上垂下的手臂)的乘积。与此同时，臂本身也承受拉伸应力，在任何高度，如果乘以面积，也就是相关的机械力，它是 $g$ 力和悬挂在机械支撑点以下的质量的乘积。机械阻力从与地板或支撑结构的接触点开始扩散，并在未支撑的端部(在从下方支撑的情况下是顶部，例如座位或地板，身体或物体悬挂部分的底部)逐渐减小到零。在压缩力被计算为负张力的情况下，每单位质量(物体各部分之间的变化，使得物体在它们之间的切片具有单位质量)在 $g$ 力方向上的张力变化率等于 $g$ 力加上切片上的非重力外力(如果有的话)(在与 $g$ 力相反的方向上被计为正)。

　　不管这个 $g$ 力是由对重力的机械阻力引起的，还是由机械力产生的坐标加速度(速度变化)引起的，或者是由这两者的组合引起的，但对于给定的 $g$ 力，应力是相同的。因此，对人们来说，无论是否引起坐标加速，所有的机械 $g$ 力都感觉完全一样。同样，对于物体来说，它们能否承受机械 $g$ 力而不损坏的问题对于任何类型的 $g$ 力都是一样的。例如，地球上的向上加速(例如，上升时速度增加，下降时速度降低)感觉就像静止在具有较高表面重力的天体上一样。引力单独作用不会产生任何 $g$ 力； $g$ 力仅由机械推拉产生。对于一个自由的物体(在空间中自由运动的物体)，这种 $g$ 力只有在 “惯性” 路径(重力的自然效应或质量惯性的自然效应)改变时才会出现。这种改变只能由重力以外的影响引起。

　　涉及 $g$ 力的重要案例包括:

作用在地球表面静止物体上的 $g$ 力是 1 $g$ (向上)，是地球表面向上的阻力反应的结果，等于加速度 1 $g$ ，与重力等大反向。数字 1 是近似值，取决于物体所处的位置。
在任何失重环境中作用在物体上的 $g$ 力，如真空中的自由落体，为 0 $g$ .
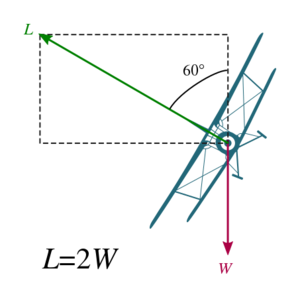
作用在具有加速度的物体上的 $g$ 力可以远大于 1，例如，右上方图片描述的在加速时可以施加 5.3 的水平 $g$ 力。
作用在具有加速度的物体上的 $g$ 力可能是向下的，例如当在过山车到达陡峭的山顶时。
如果除了重力没有其他外力，火箭中的 $g$ 力就是单位质量的推力。它的大小等于推重比乘以 g，以及单位时间消耗的 $δ v$ 。
在冲击的情况下，例如碰撞， $g$ 力在短时间内可能非常大。

　　负 $g$ 力的一个典型例子是一个完全倒置的过山车，它向地面加速(改变速度)。在这种情况下，过山车乘客的加速度比重力加速度要大，因此他们被颠倒地固定在座位上。在这种情况下，座椅施加的机械力通过以不同于重力加速度的方式改变乘客向下的路径来产生 $g$ 力。这种差异是由座位的推动造成的，提供了比重力更大的朝下的 $g$ 力。

　　牛顿运动定律描述了所有 “坐标加速度”(或没有坐标加速度)，如下:

　　第二运动定律加速度定律指出: $F = m a$ .，意味着作用在物体上的力 F 的大小等于质量 $m$ 乘以它的加速度 $a$ 。

　　第三运动定律相互作用定律指出:所有的力都成对出现，这两个力大小相等，方向相反。牛顿第三运动定律意味着，重力不仅表现为向下作用在你手中的岩石上的力，而且表现在岩石对地球施加大小相等方向相反的力。

图 2：这架特技飞机正在以+ g 的方式拉起; 除了重力之外，飞行员还在经历几 g 的惯性加速度。作用在他身上的累积垂直轴力使他暂时“体重”比正常情况多许多倍

　　在飞机上，飞行员的座位可以被认为是握着岩石的手，飞行员是岩石。当直线飞行时，水平方向有 1 $g$ 力作用于飞行员，同时他受到重力的作用。他的重力(向下的力)是 725 牛（163 磅）。根据牛顿第三定律，飞机和飞行员下方的座位提供了一个 725 牛（163 磅）的等大反向的向上推力。即使向上的速度不变，但这个机械力给飞行员提供 1.0 g 向上的加速度，(这类似于站在地面上的人，地面提供这个力和 $g$ 力)。

　　如果飞行员突然向后拉操纵杆，使他的飞机在 9.8m/s2 加速度上升，他身体上的总 $g$ 力是 2 $g$ ，其中一半来自推动飞行员抵抗重力的座位，另一半来自推动飞行员向上加速的座位，因为运动轨迹不同于自由落体轨迹，这个力实际上提供了一个加速度。从飞机的参照系来看，飞行员对座位产生 1450 牛（330 磅）的力，座位同时以相等的力向上推动飞行员。

　　当任何人乘坐车辆时，由于机械力（ $g$ 力）而产生的无阻力的加速度，因为 $g$ 力总是产生适当的加速，并且(在没有重力的情况下)通常是坐标加速度(在速度变化的情况下)。每当车辆改变方向或速度时，乘客都会感觉到座椅机械推动产生的侧向(左右)或纵向(向前和向后)力。

　　表达式 " $1 g = 9.80665 m / s^{2}$ " 意味着每过一秒钟，速度变化 9.80665 米每秒！35.30394 km/h)。速度的变化率也可以表示为 9.80665 (米每秒)每秒，或 $9.80665 m / s^{2}$ . 例如:加速度为 1 $g$ 相当于速度的变化率大约为每秒钟 35 kilometres per hour (22 miles per hour)。因此，如果汽车能够在 1 $g$ 和正在旅行 35 kilometres per hour (22 miles per hour) 它可以在一秒钟内制动到静止状态，驾驶员将经历 1 $g$ 的减速度.汽车以三倍于这个速度行驶，105 km/h (65 mph)，可以在三秒钟内制动到静止。

　　在速度在 $s$ 距离内从 0 连续增加到 $v$ ，这个加速度是 $v^{2} / (2 s)$ 。

　　引入一个变量 $g$ -耐受性，用来描述物体在受到高 $g$ 力时不会损坏，称为 $g$ 硬化。这可以应用于例如发射子弹的枪械。

3. 人体耐受性

图 3：半对数图表显示人类对线性加速度的耐受度[1]

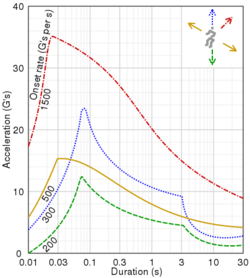
　　人的耐受性取决于 $g$ 力的大小、施加的时间长度、作用的方向、施加的位置和身体的姿势。[8][9]

　　人体是柔性和可变形的，尤其是较软的组织。一记耳光可能会短暂地在局部造成数百 $g$ 的伤害，但不会造成任何真正的伤害；然而持续一分钟 16 $g_{0}$ 有可能是致命的。当经历振动时，如果处于器官或结缔组织的共振频率，相对较低的 g 峰值水平可能会造成严重损害。

　　在某种程度上， $g$ -耐受性是可以训练的，而且个体之间的先天能力也有相当大的差异。此外，一些疾病，特别是心血管疾病会降低 $g$ -耐受性。

3.1 垂直的

　　飞机驾驶员(特别是)沿着与脊柱对齐的轴线承受的 $g$ 力。这导致受试者身体长度上的血压显著变化，从而限制了可耐受的最大 $g$ 力。

　　正的，或 “向上的” $g$ ，驱使血液向下流到坐着或站着的人的脚(更自然地，脚和身体可以被看作是被地板和座位的向上的力驱使，围绕血液向上)。对正 $g$ 的耐受性变化。一个典型的人可以忍受 5 $g_{0} (49 m / s^{2})$ (这意味着有些人在乘坐高 $g$ 过山车时可能会昏倒，在某些情况下会超过这一点),然后失去知觉，但是通过结合特殊的 g 套装和拉紧肌肉的努力——两者的作用都是迫使血液回到大脑——现代飞行员通常可以耐受持续的 9 $g_{0} (88 m / s^{2})$ 的高 $g$ 力。

　　特别是在飞机上，垂直重力通常是正的(迫使血液流向脚和远离头部)；这尤其会引起眼睛和大脑的问题。随着正垂直 $g$ 力逐渐增加(如在离心机中)，可能会出现以下症状:

灰化，视觉失去色彩，在恢复水平时容易产生视觉逆转。
隧道视觉，周边视觉逐渐丧失。
昏厥，在保持意识的同时丧失视力，由头部失血引起。
G-LOC， $g$ 力导致的意识丧失。[10]
死亡，如果 $g$ 力不迅速减少，就会发生死亡。[11]

　　对驱动血液流向头部的 “负” 或 “向下” $g$ 的阻力要低得多。此限制通常在 $- 2 t o - 3 g_{0} (- 20 t o - 29 m / s^{2})$ 范围。这种情况有时被称为红色，视觉象征性地变红[12] 因为充满血液的下眼睑被拉入视野。[13] 负 $g$ 通常是不舒服的，会造成损害。眼睛或大脑中的血管可能在血压升高时膨胀或破裂，导致视力下降甚至失明。

3.2 水平的

　　人体更擅长承受垂直于脊柱的重力。一般来说，当加速度向前时(主体基本上仰卧，通俗地说就是 “眼球向内”[14])由于视网膜中的血管在后向显得更敏感，所以显示出比加速度向后时(位于它们的前面，“眼球突出”)高得多的耐受性。

　　早期实验表明，未受过训练的人能够根据暴露时间忍受一系列加速度。这一范围从多达 20 $g_{0}$ 不到 10 秒，到 10 $g_{0}$ 一分钟，和 6 $g_{0}$ 眼球进出 10 分钟。[15] 这些力在认知设施完好无损的情况下得以忍受，因为受试者能够执行简单的身体和交流任务。尽管耐受性非常主观，但这些测试被确定不会造成长期或短期伤害，只有最有积极性的非飞行员才能完成测试。[16] 加速度先驱约翰·斯塔普在一系列火箭滑车减速实验中保持了试验水平 $g$ 力最大耐受记录，最终在 1954 年底的一次试验中达到顶峰，当时他的着陆速度为 0.9 马赫，只差一秒多一点。他经历了一次峰值为重力加速度的 46.2 倍的 “眼球外出” 加速度，超过 25 $g_{0}$ 并持续 1.1 秒，因此证明人体是有这种能力的。斯塔普又活了 45 年直到 89 岁才去世[17]，其间并没有任何不良影响。[18]

　　幸存下来的人经历的最高记录的 $g$ 力是在 2003 年 10 月 12 日德克萨斯州汽车高速公路 2003 年印地车系列决赛中，当时肯尼·布拉克驾驶的汽车与托马斯·谢克特的汽车发生了轮对轮的接触。这立即导致布拉克的车撞上了拦污栅，创下了最高纪录的 214 $g_{0}$ 。[19][20]

4. 短时间冲击、撞击和急动

　　撞击和机械冲击通常用于描述高动能冲击，即短期冲击。冲击脉冲通常通过其峰值加速度来测量 $g_{0} s$ 和脉冲持续时间。振动是一种周期性振动，也可以用 $g_{0}$ ·s 以及频率来测量。这些现象的动力学使它们区别于由相对较长加速度引起的 $g$ 力。

　　物体在从高度 $h$ 处自由落体后，随后是一段距离 d 的减速撞击，对物体的冲击大小是(h/d)* $g_{0}$ 。例如，一个坚硬紧凑的物体从 1m 处扔下，在触地 1mm 内承受 1000 $g_{0}$ 的减速度。

　　急动是加速度的变化率。以国际单位制为单位，用 m/s3 表示；它也可以用标准重力/秒( $g_{0} / s$ 。1 $g_{0} / s \approx 9.81 m / s^{3}$ )。

5. 其他生物反应

　　日本最近对极端微生物的研究涉及多种细菌(包括非极端控制的大肠杆菌)受到极端重力条件的影响。细菌在超速离心机中以 403627 $g_{0}$ 转动。脱氮副球菌是一种在超加速条件下不仅能存活，而且能促进细胞生长的细菌，这种细菌通常只能在宇宙环境中找到，例如在非常巨大的恒星或超新星的冲击波中。分析表明，小尺寸的原核细胞对于超重力条件下的成功生长至关重要。该研究对 “胚种说” 的可行性有一定的启示。[21][22]

6. 典型例子

表1：辐射的类型

例子	$g$ 力大小*
重力探测器 B 中的陀螺仪转子和导航卫星 TRIAD I 中的自由漂浮的质量证明物[23]	0 $g_{0}$
乘坐呕吐彗星号飞行器进行抛物线飞行)	$\approx 0 g_{0}$
站在月球赤道上	0.1654 $g_{0}$
站在火星赤道上	0.378 $g_{0}$
在飞机上，当飞行员按下起落架时	$\approx 0.75 g_{0}$
站在地球海平面的高度时	1 $g_{0}$
土星五号月球探测器火箭刚刚发射时	1.14 $g_{0}$
在飞机上，当飞行员拉动操纵杆上升时	$\approx 1.25 g_{0}$
布加迪威龙在 2.4s 内将速度从 0 增加到 100km/h	1.55 $g_{0}^{†}$
Gravitron 的游乐设施	2.5–3 $g_{0}$
嗅胡椒粉后不断地打喷嚏[24]	2.9 $g_{0}$
航天飞机，在发射和着陆时	3 $g_{0}$
高 g 过山车[9]	3.5–6.3 $g_{0}$
轻拍上背部的热情问候[24]	4.1 $g_{0}$
在最高燃油赛车的飙车世界纪录 4.4 秒超过 1/4 英里	4.2 $g_{0}$
第一次世界大战飞机（例如：Sopwith Camel，Fokker Dr.1，SPAD S.XIII，Nieuport 17，Albatros D.III）在混战中进行机动时。	4.5–7 $g_{0}$
雪橇的最大值预计在惠斯勒滑动中心	5.2 $g_{0}$
一级方程式赛车，在强力制动时[25]	6.3 $g_{0}$
一级方程式赛车, 侧转峰值[26]	6–6.5 $g_{0}$
全特技认证的标准滑翔机	+7/−5 $g_{0}$
阿波罗 16 号再入轨道时[27]	7.19 $g_{0}$
苏霍伊 Su-27 飞机最大允许 g 力	9 $g_{0}$
米高扬米格-35 飞机最大允许 g 力	10 $g_{0}$
红牛航空比赛飞机转弯的最大允许 g 力	10 $g_{0}$
太阳表面的重力加速度	28 $g_{0}$
Tor 导弹系统的最大 g 力[28]	30 $g_{0}$
适合人类乘坐火箭雪橇的最大 g 力	46.2 $g_{0}$
Sprint 导弹	100 $g_{0}$
在坠机中幸存了下来的人类的接触到的短暂 g 力	> 100 $g_{0}$
枪管长度为 1 公里，初速度为 6 公里/秒的空间炮（假设加速度恒定）	1,800 $g_{0}$
机械腕表的冲击能力[29][30]	> 5,000 $g_{0}$
V8 一级方程式发动机，最大活塞加速度[31]	8,600 $g_{0}$
螳螂虾，捕食时爪子的加速[32]	10,400 $g_{0}$
军用炮弹中电子元件的评级[33]	15,500 $g_{0}$
分析室底部(7.2 cm) 60000 转/分超速分析离心机[34]	300,000 $g_{0}$
大型强子对撞机中质子的平均加速度[35]	190,000,000 $g_{0}$
中子星表面的重力加速度[36]	$2.0 \times 10^{11} g_{0}$
来自威克菲尔德等离子体加速器的加速度[37]	$8.9 \times 10^{20} g_{0}$

　　 * 包括抵抗重力的贡献。

　　与水平面成 40 度角。

7. 使用加速度计进行测量

图 4：超人：六旗魔术山的逃离氪星过山车，提供 6.5 秒的弹道失重

　　加速度计最简单的形式是末端加载阻尼的弹簧，用某种方法测量特定质量的阻尼在弹簧上沿特定方向移动的距离，称为 “轴”。

　　加速度计通常被校准以测量沿一个或多个轴的重力。如果固定的单轴加速度计被定向成其测量轴是水平的，则其输出将为 0 $g$ ，如果安装在水平道路上匀速行驶的汽车上，它将继续为 0 $g$ 。当驾驶员踩下制动器或油门踏板时，加速度计将记录正加速度或负加速度。

　　如果加速度计旋转 90 度，使其垂直，即使静止不动，其读数仍为+1 $g$ 向上。在这种情况下，加速度计受到两种力的作用:重力和它所在表面的地面反作用力。由于加速度计和地面之间的机械相互作用，加速度计只能测量后一种力。如果机械只受到该力的作用，读数就是它具有的加速度。

　　如果三轴加速度计落入或以其他方式进入弹道轨道(也称为惯性轨道)，它将在所有三个轴上输出零重力加速度，因此它会像在轨道上的宇航员一样经历 “自由落体”(宇航员经历称为微重力的小潮汐加速度，为了在此作为讨论案例，大小忽略不计)。一些游乐园的游乐设施可以提供几秒钟的近似零 $g$ 。乘坐美国宇航局的 “呕吐彗星” 一次可以提供大约 25 秒钟的近似零 $g$ 。

8. 参考文献

　　 [1] ^https://web.archive.org/web/20221025123655/https://sciencing.com/convert-newtons-gforce-8720337.html.

　　 [2] ^G Force. Newton.dep.anl.gov. Retrieved on 2011-10-14..

　　 [3] ^Sircar, Sabyasachi (2007-12-12). Principles of Medical Physiology. ISBN 978-1-58890-572-7..

　　 [4] ^BIPM: Declaration on the unit of mass and on the definition of weight; conventional value of gn..

　　 [5] ^Symbol g: ESA: GOCE, Basic Measurement Units, NASA: Multiple G, Astronautix: Stapp Archived 2009-03-21 at the Wayback Machine, Honeywell: Accelerometers Archived 2009-02-17 at the Wayback Machine, Sensr LLC: GP1 Programmable Accelerometer Archived 2009-02-01 at the Wayback Machine, Farnell: accelometers, Delphi: Accident Data Recorder 3 (ADR3) MS0148 Archived 2008-12-02 at the Wayback Machine, NASA: Constants and Equations for Calculations Archived 2009-01-18 at the Wayback Machine, Jet Propulsion Laboratory: A Discussion of Various Measures of Altitude Archived 2009-02-10 at the Wayback Machine, Vehicle Safety Research Centre Loughborough: Use of smart technologies to collect and retain crash information, National Highway Traffic Safety Administration: Recording Automotive Crash Event Data Symbol G: Lyndon B. Johnson Space Center: ENVIRONMENTAL FACTORS: BIOMEDICAL RESULTS OF APOLLO, Section II, Chapter 5 Archived 2008-11-22 at the Wayback Machine, Honywell: Model JTF, General Purpose Accelerometer Archived 3 月 2, 2009 at the Wayback Machine.

　　 [6] ^"Pulling G's". Go Flight Medicine. Retrieved 24 Sep 2014..

　　 [7] ^Robert V. Brulle (2008). Engineering the Space Age: A Rocket Scientist Remembers (PDF). Air University Press. p. 135. ISBN 978-1-58566-184-8..

　　 [8] ^Balldin, Ulf I. (2002). "Chapter 33: Acceleration effects on fighter pilots." (PDF). In Lounsbury, Dave E. Medical conditions of Harsh Environments. 2. Washington, DC: Office of The Surgeon General, Department of the Army, United States of America. ISBN 9780160510717. OCLC 49322507. Retrieved 2013-09-16..

　　 [9] ^George Bibel. Beyond the Black Box: the Forensics of Airplane Crashes. Johns Hopkins University Press, 2008. ISBN 0-8018-8631-7..

　　 [10] ^Burton RR (1988). "G-induced loss of consciousness: definition, history, current status". Aviation, Space, and Environmental Medicine. 59 (1): 2–5. PMID 3281645..

　　 [11] ^The Science of G Force- Joshua Davis.

　　 [12] ^Brown, Robert G (1999). On the edge: Personal flying experiences during the Second World War. ISBN 978-1-896182-87-2..

　　 [13] ^DeHart, Roy L. (2002). Fundamentals of Aerospace Medicine: 3rd Edition. Lippincott Williams & Wilkins..

　　 [14] ^"NASA Physiological Acceleration Systems". Web.archive.org. 2008-05-20. Archived from the original on 2008-05-20. Retrieved 2012-12-25..

　　 [15] ^NASA Technical note D-337, Centrifuge Study of Pilot Tolerance to Acceleration and the Effects of Acceleration on Pilot Performance, by Brent Y. Creer, Captain Harald A. Smedal, USN (MC), and Rodney C. Vtlfngrove, figure 10.

　　 [16] ^NASA Technical note D-337, Centrifuge Study of Pilot Tolerance to Acceleration and the Effects of Acceleration on Pilot Performance, by Brent Y. Creer, Captain Harald A. Smedal, USN (MC), and Rodney C. Vtlfngrove.

　　 [17] ^Fastest Man on Earth- John Paul Stapp. Ejection Site. Retrieved on 2011-10-14..

　　 [18] ^Martin, Douglas (16 November 1999). "John Paul Stapp, 89, Is Dead; 'The Fastest Man on Earth'". The New York Times. Retrieved 29 October 2016..

　　 [19] ^"New details from horror crash". News.com.au. Retrieved 30 December 2017..

　　 [20] ^"Q&A: Kenny Brack". Crash.net. 13 October 2004. Retrieved 30 December 2017..

　　 [21] ^Than, Ker (25 April 2011). "Bacteria Grow Under 400,000 Times Earth's Gravity". National Geographic- Daily News. National Geographic Society. Retrieved 28 April 2011..

　　 [22] ^Deguchi, Shigeru; Hirokazu Shimoshige; Mikiko Tsudome; Sada-atsu Mukai; Robert W. Corkery; Susumu Ito; Koki Horikoshi (2011). "Microbial growth at hyperaccelerations up to 403,627 × g". Proceedings of the National Academy of Sciences. 108 (19): 7997–8002. Bibcode:2011PNAS..108.7997D. doi:10.1073/pnas.1018027108. PMC 3093466. PMID 21518884. Retrieved 28 April 2011..

　　 [23] ^Stanford University: Gravity Probe B, Payload & Spacecraft, and NASA: Investigation of Drag-Free Control Technology for Earth Science Constellation Missions. The TRIAD 1 satellite was a later, more advanced navigation satellite that was part of the U.S. Navy’s Transit, or NAVSAT system..

　　 [24] ^Allen M.E.; Weir-Jones I; et al. (1994). "Acceleration perturbations of daily living. A comparison to 'whiplash'". Spine. 19 (11): 1285–1290. PMID 8073323..

　　 [25] ^FORMULA 1 (31 March 2017). "F1 2017 v 2016: G-Force Comparison". YouTube. Retrieved 30 December 2017..

　　 [26] ^6 g0 has been recorded in the 130R turn at Suzuka circuit, Japan. "Archived copy". Archived from the original on 2010-02-28. Retrieved 2012-10-12.CS1 maint: Archived copy as title (link) Many turns have 5 g0 peak values, like turn 8 at Istanbul or Eau Rouge at Spa.

　　 [27] ^NASA: Table 2: Apollo Manned Space Flight Reentry G Levels Lsda.jsc.nasa.gov. [28] ^"Russia trains Greek Tor-M1 crews". RIA Novosti. 2007-12-27. Retrieved 2008-09-04..

　　 [29] ^"OMEGA Watches: FAQ". Web.archive.org. 10 February 2010. Archived from the original on 10 February 2010. Retrieved 30 December 2017.CS1 maint: BOT: original-url status unknown (link).

　　 [30] ^"Welcome to BALL Watch - Shock Resistance". Ballwatch.com. Retrieved 30 December 2017..

　　 [31] ^"F1: Stunning data about the Cosworth V-8 Formula 1 engine - Auto123.com". Auto123.com. Retrieved 30 December 2017..

　　 [32] ^S. N. Patek, W. L. Korff & R. L. Caldwell (2004). "Deadly strike mechanism of a mantis shrimp" (PDF). Nature. 428 (6985): 819–820. Bibcode:2004Natur.428..819P. doi:10.1038/428819a. PMID 15103366..

　　 [33] ^"L3 IEC". Iechome.com. Archived from the original on 2011-02-21. Retrieved 30 December 2017..

　　 [34] ^(rpm·π/30)2·0.072/g.

　　 [35] ^(7 TeV/(20 minutes·c))/proton mass.

　　 [36] ^Green, Simon F.; Jones, Mark H.; Burnell, S. Jocelyn (2004). An Introduction to the Sun and Stars (illustrated ed.). Cambridge University Press. p. 322. ISBN 978-0-521-54622-5. Extract of page 322 note: 2.00×1012 ms−2 = 2.04×1011 g0.

　　 [37] ^(42 GeV/85 cm)/electron mass.