复旦大学 1999 量子真题
贡献者: 待更新
声明:“该内容来源于网络公开资料,不保证真实性,如有侵权请联系管理员”
(1) 设 $t=0$ 时,粒子处于 $\psi(x) = \sin\left(kx\right) + \frac{1}{3}\cos^2(kx)$,求粒子动能和动能的平均值。(20 分)
(2) 利用测不准关系(或不确定性原理)估算线原子的基态能量。(20 分)
(3) 试在 $\sigma_y$ 表象中,求 $\sigma_z$ 的矩阵元。(20 分)
(4) 设体系哈密顿算符矩阵在能量表象中为矩阵 $\begin{pmatrix}E_1^0 + a & b \\\\b & E_2^0 + a\end{pmatrix}$ 其中 $a, b$ 为实数,试用微扰论公式求能量至二级修正值。(20 分)
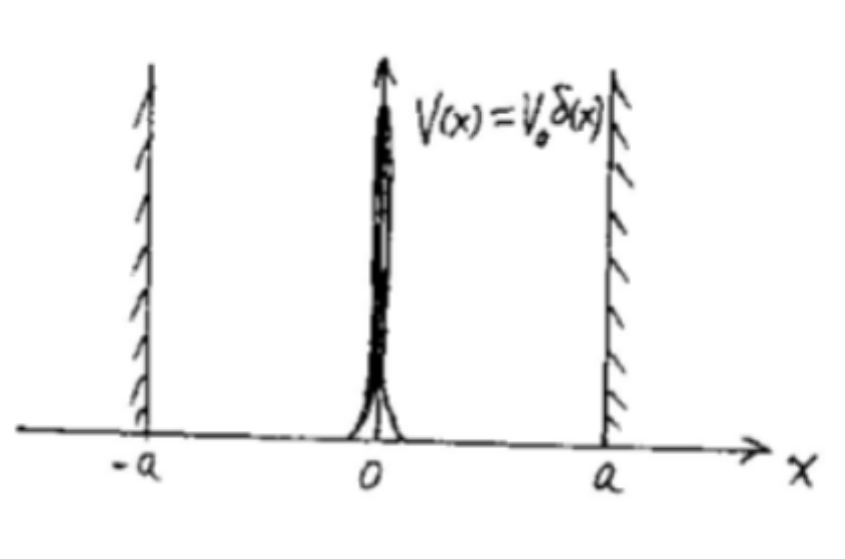
(5) 若在宽度为 $2a$ 的无穷深方势阱的中心位置加入 $V_0 \delta(x)$ 势,同对于无穷深方势阱的原本能级有何影响。(20 分)
图 1:请添加图片标题