狄拉克之海
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译)
狄拉克之海是真空的理论模型,它是一个由负能量粒子组成的无限海洋。它首先是由英国物理学家保罗狄拉克在 1930 年[1] 为了解释狄拉克方程的相对论电子解中出现的反常的负能量态而提出的真空理论假设。[2] 正电子,电子的反物质粒子,在 1932 年实验发现之前,就被认为是狄拉克海中的一个洞。
在求解 3 动量平面波动解的自由狄拉克方程时, $$i \hbar \frac{\partial \Psi}{\partial t} = (c \alpha \cdot \hat{p} + mc^2 \beta) \Psi~,$$ 人们发现 $$\Psi_{p \lambda} = N \left( \begin{array}{c} U \\ \frac{(c \hat{\sigma} \cdot \mathbf{p})}{mc^2 + \lambda E_p} U \end{array} \right)\frac{\exp\left[ i ( \mathbf{p} \cdot \mathbf{x} - \epsilon t ) / \hbar \right]}{\sqrt{2 \pi \hbar}^3}~,$$ 其中 $$\epsilon = \pm E_p, \quad E_p = +c \sqrt{\mathbf{p}^2 + m^2 c^2}, \quad \lambda = \text{sgn} \, \epsilon~$$ 这是相对论能量动量关系的直接结果 $$E^2 = p^2 c^2 + m^2 c^4~$$
狄拉克方程就是建立在这个基础上的。量 U 是常数 $2\times1$ 列向量,N 是归一化常数。量 $\epsilon$ 被称为时间演化因子,它在薛定谔方程的平面波解中的类似作用解释为波(粒子)的能量。这种解释在这里不能立即得到,因为它可能获得负值。克莱因-戈登方程也存在类似的情况。在这种情况下,$\epsilon$ 的绝对值在正则的形式中可以解释为波的能量,负ε的波实际上具有正能量 Ep。[4] 但是狄拉克方程却不是这样。与负ε相关的正则形式中的能量是-Ep。[5]
在空穴理论中,具有负时间演化因子的解被重新解释为正电子的表示,这由卡尔·安德森发现。对这个结果的解释需要狄拉克之海(Dirac sea),表明狄拉克方程不仅仅是狭义相对论和量子力学的结合,还意味着粒子的数量不能守恒。[6]
1. 起源
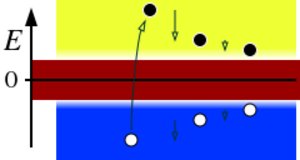
狄拉克之海源于狄拉克方程的能谱,狄拉克方程是薛定谔方程在狭义相对论下的延伸,狄拉克在 1928 年提出了这个方程。虽然这个方程在描述电子动力学方面非常成功,但它有一个相当奇特的特征:对于每个具有正能量 E 的量子态,都有一个对应的能量-E 态。当考虑一个孤立的电子时,这并不是一个很大的困难,因为它的能量是守恒的,负能量电子可能会被遗漏。然而,当考虑电磁场的影响时,困难就出现了,因为正能量电子能够通过连续发射光子来释放能量,随着电子下降到越来越低的能量状态,这一过程可以无限制地继续下去。真正的电子显然不是这样。
狄拉克对此的解决方案是求助于泡利不相容原理。电子是费米子,遵守不相容原理,这意味着在一个原子中没有两个电子可以共享一个能量状态。狄拉克假设我们认为的 “真空” 实际上是所有负能量态都被填满的状态,而没有正能量态。因此,如果我们想引入一个电子,我们必须把它置于正能量状态,因为所有的负能量状态都被占据了。此外,即使电子因发射光子而失去能量,也将被不允许降到零能量以下。
狄拉克还指出,可能存在这样一种情况,即除了一个负能量态之外,所有的负能量态都被占据了。负能量电子海洋中的这个 “空穴” 会对电场做出反应,就好像它是一个带正电荷的粒子。最初,狄拉克认为这个洞是质子。然而,罗伯特·奥本海默(Robert Oppenheimer)指出,一个电子和它的空穴能够互相湮没,在高能光子的形式中以电子的静止能量的顺序释放能量;如果空穴是质子,稳定的原子就不存在。[7] 赫尔曼·韦勒还指出,一个空穴应该像电子一样具有相同的质量,而质子大约比它们重两千倍。终于,卡尔安德森于 1932 年发现了正电子,这个问题得到了解决,同时预测的狄拉克空穴所有物理性质得到了证实。
2. 狄拉克之海的丑陋
尽管取得了成功,迪拉克之海的概念并没有给人以优雅的印象。海洋的存在意味着充满整个空间的无限负电荷。为了搞清楚这一点,我们必须假设 “真空” 必须具有无限的正电荷密度,而这恰好被狄拉克海抵消了。由于绝对能量密度是不可观测的——撇开宇宙常数不谈——真空的无限能量密度并不是一个问题。只要能观察到能量密度的变化。杰弗里·兰蒂斯(一部艰难的科幻短篇小说《狄拉克海的涟漪》的作者)也指出,泡利不相容原理并不一定意味着充满负电子的狄拉克之海不能接受更多的电子,因为正如希尔伯特所阐明的,即使充满了负电子,无限量的海洋也能接受新粒子。当我们有一个手性异常和一个标准瞬子时,就会发生这种情况。
量子场论(QFT)在 20 世纪 30 年代的发展使得重新表述狄拉克方程成为可能,QFT 将正电子视为 “真实的” 粒子而不是虚幻的粒子,并使真空成为没有粒子而不是无限粒子海的状态。这种理论更有说服力,尤其是因为它再现了狄拉克之海的所有合理预测,如电子正电子互相湮没。另一方面,场公式并没有消除狄拉克之海带来的所有困难;特别是具有无限能量的真空问题。
3. 现代诠释
狄拉克海解释和现代 QFT 解释是通过一个非常简单的博戈柳波夫变换联系在一起的,博戈柳波夫变换是两种不同自由场理论的产生和湮没算符之间的一种识别。在现代解释中,狄拉克自旋的场算符是产生算符和湮没算符的总和,用示意图表示: $$\psi(x) = \sum a^\dagger(k)e^{ikx} + a(k)e^{-ikx}~$$ 负频率的算符降低任何状态的能量,且降低量与频率成正比,而正频率的算符提高任何状态的能量。
在现代解释中,正频率算子增加一个正能量粒子,增加能量,而负频率算符湮没一个正能量粒子,降低能量。对于费米场,产生算符 $a\dagger(k)$ 当动量为 k 的状态已经填满时,给出零,而湮没算符 $a(k)$ 当动量 k 为 0 时给出零。
但是这样就有可能把湮没算符重新解释为负能量粒子的产生算符。它仍然会降低真空的能量,但从这个角度来看,它是通过创造一个负能量物体来实现的。这种重新解释只会影响哲学。为了重塑真空中湮没算符给 0 值的规则,负能量态的 “空” 和 “满” 的概念必须颠倒过来。这些不是没有反粒子的状态,而是已经充满了负能量粒子的状态。
代价是在某些表达式中有不均匀性,因为用产生算符代替湮没算符增加了负能量粒子数的常数。费米场的数算符[8] 是: $${N} = {a}^\dagger {a} = 1 - {a} {a}^\dagger~$$ 也就是说,如果对负能量态用 1-N 代替 N,像能量密度和电荷密度这样的量会有一个常数变化,这些量是计算粒子总数的。无限常数赋予狄拉克海无限的能量密度和电荷密度。真空电荷密度应该为零,因为真空是洛伦兹不变量,但这是在狄拉克理论中的人为调整。这样就过渡到了现代理论的解释。
狄拉克的想法更直接地适用于固态物理,在固态物理中,固体中的价带可以被视为电子的 “海洋”。海洋中确实存在空穴,这对理解半导体的作用极其重要,尽管它们从来没有被称为 “正电子”。与粒子物理学不同,有一种潜在的正电荷——离子晶格的电荷——抵消了海洋的电荷。
4. 因果费米子系统理论的复兴
狄拉克最初关于粒子海的概念在因果费米子系统理论中复活了,这是最近提出的统一物理理论。在这种理论中,狄拉克海的无限真空能量和无限电荷密度的问题消失了,因为这些差异从通过因果作用原理制定的物理方程中消失了。[9] 这些方程不需要预先存在的时空,使得人们意识到有可能时空和其中的所有结构是海洋状态相互之间以及与海洋中的额外粒子和 “洞” 共同作用的结果。
5. 评论
- This was not the original intent of Dirac though, as the title of his 1930 paper (A Theory of Electrons and Protons) indicates. But it soon afterwards became clear that the mass of holes must be that of the electron.
6. 参考文献
[1] ^Dirac 1930.
[2] ^Greiner 2000.
[3] ^Greiner 2000,第 107–109 页.
[4] ^Greiner 2000,第 15 页.
[5] ^Greiner 2000,第 117 页.
[6] ^Alvarez-Gaume & Vazquez-Mozo 2005.
[7] ^Dirac 1931.
[8] ^Sattler 2010.
[9] ^Finster 2011.