简单的扩散与混合模拟器(MATLAB)
贡献者: ACertainUser; addis
1. 混合模拟器
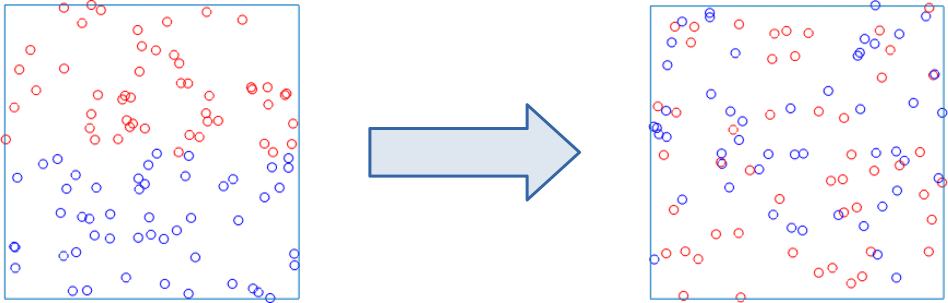
图 1:混合
本 Matlab 程序简易地模拟了容器中粒子的随机运动,直观地反映了统计力学中家喻户晓的基本问题:为什么微观上粒子的运动看似毫无规律,而宏观上物质的变化却体现出方向性?
本程序假设粒子的速度都是相同的,且粒子间没有相互作用。严格地说,这其实并不满足麦克斯韦分布与近独立系统(粒子间有微弱的相互作用力以使系统能够趋近热力学平衡)假设。
clc
clear
global N;
global points;
global h
global dt;
function draw() %绘制粒子图像
global N;
global points;
global h;
hold on
axis equal
axis([-0.1 1.1 -0.1 1.1])
for n = 1:N
h(n)=scatter(points(1,n),points(2,n));
set(h(n),'SizeData',16);
if points(5,n)==1;
set(h(n),'MarkerEdgeColor','r');
else
set(h(n),'MarkerEdgeColor','b');
end
end
line([0 1], [0 0]) %绘制容器边框
line([0 0], [0 1])
line([0 1], [1 1])
line([1 1], [0 1])
end
function update() %更新粒子图像
global N;
global points;
global h;
for n = 1:N
set(h(n),'XData',points(1,n));
set(h(n),'YData',points(2,n));
end
end
function run() %更新粒子的位置与速度
global N;
global points;
global dt
for n = 1:N
points(1,n) +=points(3,n)*dt; %位移=速度*时间
points(2,n) +=points(4,n)*dt;
if points(1,n) < 0 || points(1,n) > 1 %碰撞容器壁使速度反向
points(3,n) = -points(3,n);
end
if points(2,n) < 0 || points(2,n) > 1
points(4,n) = -points(4,n);
end
end
end
N=100;
points=zeros(5,N); %x,y,vx,vy,type
dt = 0.005;
for n = 1:N %随机创建粒子
angle = 2*pi*rand();
points(1,n)=rand();
points(2,n)=rand();
points(3,n)=cos(angle);
points(4,n)=sin(angle);
if points(2,n)>0.5 %将处于容器上方的粒子设为类型1,处于容器下方的粒子设为类型2.
points(5,n)=1;
else
points(5,n)=2;
end
end
draw();
n=1;
while true
run();
update();
drawnow;
pause(0.01);
end
2. 扩散模拟器
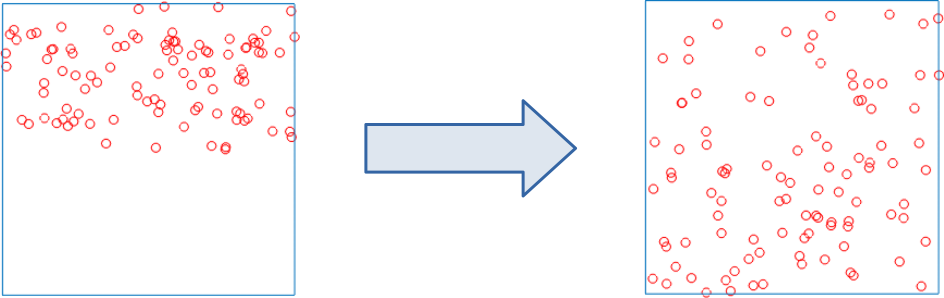
图 2:扩散
将创建粒子的代码稍加修改,就可以模拟扩散现象:
points(2,n)= 0.5*rand() + 0.5; %所有粒子的y坐标都处于 (0.5, 1) 范围,即所有粒子初始时仅分布在上半容器。