电磁感应
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译)
电磁感应是在变化的磁场中跨越电导体产生的电动势(即电压)。
麦可·法拉第通常被认为是 1831 年感应的发现,和詹姆斯·克拉克·麦克斯韦数学上将其描述为法拉第感应定律。楞次定律描述感应场的方向。法拉第定律后来被推广为麦克斯韦-法拉第方程,这四个方程之一麦克斯韦方程在他的理论中电磁。
电磁感应有许多应用,包括电气元件如电感器和变压器,以及设备如电动机和发电机。
1. 基本概念
1831 年,一位叫迈克尔·法拉第的科学家发现了磁与电之间的相互联系和转化关系。只要穿过闭合电路的磁通量发生变化,闭合电路中就会产生感应电流。这种利用磁场产生电流的现象称为电磁感应(Electromagnetic induction),产生的电流叫做感应电流。
电磁感应现象的产生条件有两点(缺一不可)。
- 闭合电路。
- 穿过闭合电路的磁通量发生变化。
让磁通量发生变化的方法有两种。一种方法是让闭合电路中的导体在磁场中做切割磁感线的运动;另一种方法是让磁场在导体内运动。
1.1 磁通量
设在匀强磁场中有一个与磁场方向垂直的平面,磁场的磁感应强度为 $ B $,平面的面积为 $S $。
(1) 定义:在匀强磁场中,磁感应强度 $ B $) 与垂直磁场方向的面积 $ S $ 的乘积,叫做穿过这个面的磁通量,简称磁通。
(2) 定义式: $\varphi = B \cdot S$
当平面与磁场方向不垂直时 $\varphi = B \cdot S = BS \cos \theta$
(( $\theta$) 为平面的垂线与磁场方向的夹角)
(3) 物理意义
垂直穿过某个面的磁感线条数表示穿过这个面的磁通量。
(4) 单位:在国际单位制中,磁通量的单位是韦伯,简称韦,符号是 Wb。
1 Wb = 1 T·m2 = 1 V·s。
(5) 标量性:磁通量是标量,但是有正负之分。
1.2 现象
(1)电磁感应现象:闭合电路中的一部分导体做切割磁感线运动,电路中产生感应电流。
(2)感应电流:在电磁感应现象中产生的电流。
(3)产生电磁感应现象的条件:
①两种不同表述
a.闭合电路中的一部分导体与磁场发生相对运动
b.穿过闭合电路的磁场发生变化
②两种表述的比较和统一
a.两种情况产生感应电流的根本原因不同
闭合电路中的一部分导体与磁场发生相对运动时,是导体中的自由电子随导体一起运动,受到的洛伦兹力的一个分力使自由电子发生定向移动形成电流,这种情况产生的电流有时称为动生电流。
穿过闭合电路的磁场发生变化时,根据电磁场理论,变化的磁场周围产生电场,电场使导体中的自由电子定向移动形成电流,这种情况产生的电流称为感应电流或感生电流。
b.两种表述的统一
两种表述可统一为穿过闭合电路的磁通量发生变化。
③产生电磁感应现象的条件
不论用什么方法,只要穿过闭合电路的磁通量发生变化,闭合电路中就有电流产生。
条件:a.闭合电路;b.一部分导体;c.做切割磁感线运动
1.3 能量的转化
能的转化守恒定律是自然界普遍规律,同样也适用于电磁感应现象。
1.4 感应电动势
(1)定义:在电磁感应现象中产生的电动势,叫做感应电动势。方向是由低电势指向高电势。
(2)产生感应电动势的条件:穿过回路的磁通量发生变化。
(3)物理意义:感应电动势是反映电磁感应现象本质的物理量。
(4)方向规定:内电路中的感应电流方向,为感应电动势方向。
(5)反电动势:在电动机转动时,线圈中也会产生感应电动势,这个感应电动势总要削弱电源电动势的作用,这个电动势称为反电动势。
2. 历史
电磁感应是由麦可·法拉第于 1831 年发现的。[1][2]它是由约瑟夫·亨利于 1832 年独立发现的。[3][4]
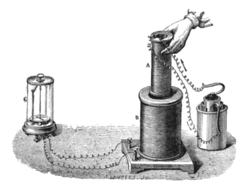
在法拉第的第一次实验演示中(1831 年 8 月 29 日),他将两条电线缠绕在铁环或 “圆环” 的相对两侧(这种布置类似于现代的环形变压器)。[来源请求]基于他对电磁体的理解,他预计当电流开始在一根导线中流动时,一种波将穿过环,并在相对侧产生一些电效应。他将一根电线插入检流计,并在将另一根电线连接到电池时观察它。当他将电线连接到电池上时,他看到了一个瞬时电流,他称之为 “电波”,当他断开电池时,他看到了另一个瞬时电流。[5]这种感应是由于电池连接和断开时发生的磁通量变化。[6]两个月内,法拉第发现了电磁感应的其他几种表现形式。例如,当他快速将条形磁铁推入和拉出线圈时,他看到了瞬态电流,并且他通过用滑动的电导线旋转条形磁铁附近的铜盘(“法拉第盘”)产生了稳定的( DC )电流。[7]
法拉第用一个他称之为磁力线的概念解释了电磁感应。然而,当时的科学家普遍拒绝接受他的理论观点,主要是因为它们不是数学公式。[8]一个例外是詹姆斯·克拉克·麦克斯韦,他使用法拉第的思想作为他定量电磁理论的基础。[8][9][10]在麦克斯韦的模型中,电磁感应的时变方面被表示为微分方程,奥利弗·亥维赛称之为法拉第定律,尽管它与法拉第的原始公式略有不同,并且没有描述。Heaviside 的版本(见下面的)是今天在被称为麦克斯韦方程组的方程组中公认的形式。
1834 年,海因里希·楞次制定了以他的名字命名的定律来描述 “通过电路的通量”。楞次定律给出了由电磁感应产生的感应电动势和电流的方向。
3. 理论
3.1 法拉第感应定律和楞次定律
法拉第感应定律利用了磁通量 $\phi_B$ 穿过由线环包围的空间区域。磁通量由表面积分定义:[11]
在哪里 $dA$ 是由线环包围的表面 $\sigma$ 的元素,$B$ 是磁场。点积 $BdA$ 对应于无穷小量的磁通量。更直观地说,通过线圈的磁通量与通过线圈的磁力线的数量成正比。
当通过表面的磁通量变化时,法拉第感应定律说线环获得了一个电动势。[12]该定律最广泛的版本是,任何闭合电路中的感生电动势等于电路包围的磁通量的变化率:[13][14]
在哪里 是电动势和 $\phi_B$ 是磁通量。电动势的方向由楞次定律给出,它指出感应电流将沿着与产生它的变化相反的方向流动。[15]这是由于前面等式中的负号。为了增加产生的电动势,一种常见的方法是利用磁链,方法是创建一个紧密缠绕的线圈,包括 N 相同的匝数,每一个都有相同的磁通量通过。由此产生的电动势为 N 是单线的数倍。[16][17]
通过线圈表面磁通量的变化产生电动势有几种方法:
- 磁场 $\mathbf B$ 变化(例如交变磁场,或者将线圈向 B 场更强的条形磁铁移动),
- 线环变形并且表面 $\sigma$ 改变,
- 表面的方向 $dA$ 变化(例如将线圈旋转成固定磁场),
- 以上任何组合
3.2 麦克斯韦-法拉第方程
一般来说,电动势 $\mathcal{E}$ 在环绕表面的线环中 $\sigma$,和电场 $E$ 在导线中由下式给出 $$\mathcal{E} = \oint_{\sigma} \mathbf{E} \cdot d\mathbf{l}~$$ 在哪里 $\alpha$ 是表面轮廓的一个元素 $\sigma$ 结合通量的定义
我们可以写出麦克斯韦-法拉第方程的积分形式: $$\oint_{\partial \Sigma} \mathbf{E} \cdot d\mathbf{l} = -\frac{d}{dt} \int_{\Sigma} \mathbf{B} \cdot d\mathbf{A}~$$ 它是四大麦克斯韦方程组之一,因此在经典电磁学理论中起着基础性作用。
3.3 法拉第定律和相对论
法拉第定律描述了两种不同的现象运动电动势由移动电线上的磁力产生(参见洛伦兹力),而变压器电动势这是由于磁场的变化(由于麦克斯韦-法拉第方程的微分形式,)引起的。詹姆斯·克拉克·麦克斯韦在 1861 年引起了人们对不同物理现象的注意。[18][19]这被认为是物理学中引用这样一个基本定律来解释两种不同现象的一个独特例子。[20]
爱因斯坦注意到这两种情况都对应于导体和磁体之间的相对运动,并且结果不受哪个运动的影响。这是导致他发展狭义相对论的主要途径之一。[21]
4. 应用程序
- Current clamp
- Electric generators
- Electromagnetic forming
- Graphics tablet
- Hall effect meters
- Induction cooking
- Induction motors
- Induction sealing
- Induction welding
- Inductive charging
- Inductors
- Magnetic flow meters
- Mechanically powered flashlight
- Pickups
- Rowland ring
- Transcranial magnetic stimulation
- Transformers
- Wireless energy transfer
4.1 发电机
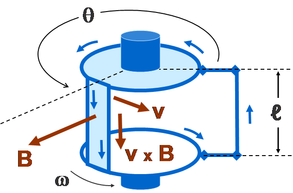
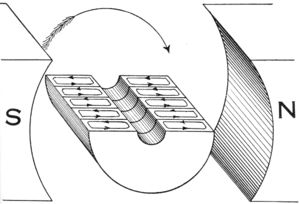
由于电路和磁场的相对运动而由法拉第感应定律产生的电动势是发电机下面的现象。当永磁体相对于导体运动时,或者反之亦然,产生电动势。如果电线通过电负载连接,电流将流动,从而产生电能,将运动的机械能转换成电能。例如鼓式发电机基于右下角的数字。这一思想的另一种实现是右边以简化形式显示的法拉第圆盘。
在法拉第圆盘的例子中,圆盘在垂直于圆盘的均匀磁场中旋转,由于洛伦兹力,导致电流在旋臂中流动。驱动这种电流需要机械功。当产生的电流流过导电边缘时,通过安培定律的电流产生磁场(图中标记为 “感应 B”)。因此,边缘变成了阻止盘旋转的电磁铁(例如楞次定律)。在图的远侧,返回电流从旋转臂通过边缘的远侧流向底部电刷。由该返回电流感应的 B 场与施加的 B 场相反,趋向于减少通过电路一侧通量,与提高由于旋转而流动。在图的近侧,返回电流从旋转臂通过边缘的近侧流向底部电刷。感应 B 场增加电路这一侧的通量,与减少由于 r 的旋转而流动。尽管有这种反作用力,保持光盘移动所需的能量正好等于产生的电能(加上由于摩擦、焦耳加热和其他低效率而浪费的能量)。所有将机械能转化为电能的发电机都有这种现象。
4.2 电力变压器
当线圈中的电流变化时,变化的电流产生变化的磁场。到达该磁场的第二根导线将经历磁场的这种变化,作为其耦合磁通量的变化,dφB/d t。因此,在第二个回路中建立起电动势,称为感应电动势或变压器电动势。如果该回路的两端通过电负载连接,电流将会流动。
电流箝位
电流钳是一种具有分裂铁芯的变压器,可以将分裂铁芯散开并夹在电线或线圈上,以测量其中的电流,或者相反,感应电压。与传统仪器不同,夹具不与导体电接触,也不需要在夹具连接期间将其断开。
4.3 磁流量计
法拉第定律用于测量导电液体和泥浆的流量。这种仪器被称为磁流量计。磁场中产生的感应电压 $\varepsilon B$ 由于导电液体以一定速度移动 v 由下式给出:
$$\varepsilon = B \cdot L \cdot v~$$
其中 $B$ 是磁流量计中电极之间的距离。
5. 涡流
在均匀磁场中移动或在变化磁场中静止的导体(有限尺寸)将在其中感应出电流。这些感应涡流可能是不理想的,因为它们会消耗导体电阻中的能量。有许多方法用来控制这些不期望的感应效应。
- 电动机、发电机和变压器中的电磁体不使用固体金属,而是使用薄金属板,称为层压。如下所述,这些薄板减少了寄生涡流。
- 电子设备中的感应线圈通常使用磁芯来最小化寄生电流。它们是金属粉末和树脂粘合剂的混合物,可以保持任何形状。粘合剂防止寄生电流流过粉末金属。
5.1 电磁叠片
当固体金属块在磁场中旋转时,会产生涡流,因为金属的外部比内部切割更多的磁力线,因此感生电动势不均匀,倾向于在最大和最小电势点之间建立电流。涡流消耗大量能量,通常会导致有害的温度上升。[22]
在这个例子中只显示了五个叠片或板,以便显示涡流的细分。在实际使用中,叠片或冲片的数量从每英寸 40 到 66 个不等,并且使涡流损耗降低到大约 1%。虽然极板可以通过绝缘隔离,但电压太低,极板的自然生锈/氧化层足以防止电流流过叠片。[22]
这是一个转子,直径约为 20 毫米,来自一个用于 CD player.注意电磁极片的叠片,用于限制寄生电感损耗。
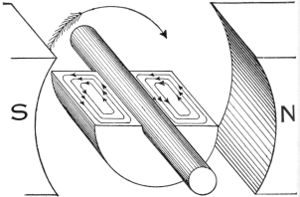
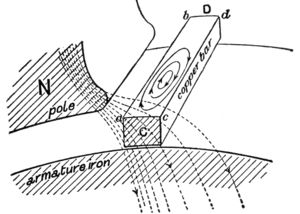
5.2 导体内部的寄生感应
在这个例子中,旋转电枢上的实心铜条导体正好穿过磁场磁体极片 N 的尖端下方。注意铜棒上力线的不均匀分布。磁场在铜棒(a,b)的左边缘更集中,因此更强,而在右边缘(c,d)磁场更弱。由于铜棒的两个边缘以相同的速度移动,铜棒上场强的这种差异在铜棒内产生螺纹或电流涡流。[22]
大电流工频设备,如电动机、发电机和变压器,使用多个并联的小导体来阻断大固体导体中可能形成的涡流。同样的原理也适用于高于电源频率的变压器,例如,无线电接收机的开关电源和中频耦合变压器中使用的变压器。
6. 参考文献
[1] ^Ulaby, Fawwaz (2007). Fundamentals of applied electromagnetics (5th ed.). Pearson:Prentice Hall. p. 255. ISBN 0-13-241326-4..
[2] ^"Joseph Henry". Distinguished Members Gallery, National Academy of Sciences. Archived from the original on 2013-12-13. Retrieved 2006-11-30..
[3] ^"A Brief History of Electromagnetism" (PDF)..
[4] ^"Electromagnetism". Smithsonian Institution Archives..
[5] ^麦可·法拉第,作者:皮尔斯·威廉姆斯,第 182-3 页.
[6] ^Giancoli, Douglas C. (1998). Physics: Principles with Applications (Fifth ed.). pp. 623–624..
[7] ^麦可·法拉第,作者:皮尔斯·威廉姆斯,第 191-5 页.
[8] ^麦可·法拉第,作者:皮尔斯·威廉姆斯,第 510 页.
[9] ^麦克斯韦,詹姆斯·克拉克(1904),《电与磁论》,第二卷,第三版。牛津大学出版社,第 178-9 和 189 页。.
[10] ^《档案传记:麦可·法拉第》,英国工程技术学会。.
[11] ^Good, R. H. (1999). Classical Electromagnetism. Saunders College Publishing. p. 107. ISBN 0-03-022353-9..
[12] ^The EMF is the voltage that would be measured by cutting the wire to create an open circuit, and attaching a voltmeter to the leads. Mathematically, is defined as the energy available from a unit charge that has traveled once around the wire loop.[13][14][15].
[13] ^Jordan, E.; Balmain, K. G. (1968). Electromagnetic Waves and Radiating Systems (2nd ed.). Prentice-Hall. p. 100..
[14] ^Hayt, W. (1989). Engineering Electromagnetics (5th ed.). McGraw-Hill. p. 312. ISBN 0-07-027406-1..
[15] ^Schmitt, R. (2002). Electromagnetics Explained. p. 75..
[16] ^Whelan, P. M.; Hodgeson, M. J. (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 0-7195-3382-1..
[17] ^Nave, C. R. "Faraday's Law". HyperPhysics. Georgia State University. Retrieved 2011-08-29..
[18] ^Maxwell, J. C. (1861). "On physical lines of force". Philosophical Magazine. 90: 11–23. doi:10.1080/1478643100365918..
[19] ^Griffiths, D. J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. pp. 301–303. ISBN 0-13-805326-X.请注意,这篇文章称之为 “法拉第定律” 的有关磁通量的定律被格里菲斯称为 “通用磁通量定律”。他使用术语 “法拉第定律” 来指代本文所称的 “麦克斯韦-法拉第方程”。.
[20] ^“磁通量规则” 是费曼用来指代磁通量与电动势相关联的定律的术语。Feynman, R. P.; Leighton, R. B.; Sands, M. L. (2006). The Feynman Lectures on Physics, Volume II. Pearson/Addison-Wesley. p. 17-2. ISBN 0-8053-9049-9..
[21] ^Einstein, A. (1905). "Zur Elektrodynamik bewegter Körper". Annalen der Physik. 17 (10): 891–921. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004. 翻译成 Einstein, A. (1923). "On the Electrodynamics of Moving Bodies" (PDF). The Principle of Relativity. Jeffery, G.B.; Perret, W. (transl.). London: Methuen and Company..
[22] ^图片和参考文本来自公共领域书籍:霍金斯电气指南,第 1 卷,第 19 章:电枢理论,第 270-273 页,西奥版权所有 1917。美国印刷的奥德尔公司.