竖直面内的圆周运动(高中)
贡献者: Connection
- 本文存在未完成的内容。
1. 引言
本文主要介绍竖直平面内变速圆周运动的临界问题。这类问题常有如下设问:“如图所示........若物块不脱离轨道,求轨道半径 R 的取值范围”。这个问题也是高中物理的一个重要模型,常作为综合性大题的一个组成部分,与动能定理、动量定理、动量守恒定律、带电粒子运动、电磁感应等知识点共同用作命题。
2. 能量观点的引入
常见的竖直面内圆周运动模型有绳模型、杆模型、内轨模型、外轨模型等,无论什么模型,竖直面内受重力作用的物体总是做变速圆周运动,我们无法写出一个一劳永逸的描述物体运动特征的函数解析式。想要解决与之有关的临界问题,至少在高中范围内(截止 2024 年的普通高中物理教科书),不用能量观点,我们无从下手。
3. 绳模型可能运动 1-往复运动
现在考察一个具体物理情境与实例。
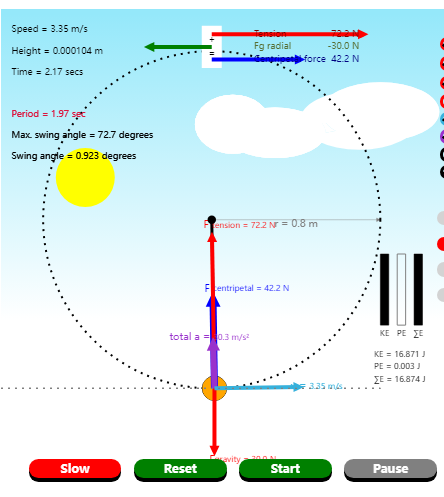
如图 1 所示,一质量为 $m$ 的小球从半径为 $R$ 的固定光滑圆轨道的最低点 $A$ 点,以速度 $ \boldsymbol{\mathbf{v}} _0$ 向右运动,忽略空气阻力,若它运动过程中不脱离圆形轨迹,试分析(大致想象)小球的运动情景。
首先可以设想,当时间开始流动,小球迅速开始向右运动。若无绳子束缚,它将向右水平飞出,也即沿圆形轨迹点 A 处切线飞出。由于绳的拉力,小球会有向心运动趋势,对其进行受力分析,则绳拉力充当向心力。在一个微小的时间微元后,小球正好行走了一小段圆弧。当时间 t 足够大时,小球将会达到圆形轨迹右下方四分之一圆弧的某处。
这时我们立即注意到,在此过程中机械能守恒且重力做功,小球做变速圆周运动,合加速度指向屏幕左侧,速率逐渐减小。
于是我们自然想到,存在一个速度临界值 $ \boldsymbol{\mathbf{v}} _1$,使得小于这个临界值的所有初速度 $v_0$ 都会让小球无法通过与圆心等高处,只能以类似于单摆的方式往复运动。
此时小球无论如何也无法脱离轨道,因为此过程中重力的向心分量使小球有紧压轨道的趋势。
现在我们尝试求出这个临界值 $ \boldsymbol{\mathbf{v}} _1$。尽管我们进行了受力分析,由几何关系可以列出牛顿第二定律的方程(设绳子拉力为 $ \boldsymbol{\mathbf{T}} $,小球与竖直方向偏转角为 $\theta$): $$ \left \{ \begin{aligned} F&=m\frac{v^2}{R}\\ F&=T-mg cos \theta \\ \end{aligned} \right. ~, $$ 但由这个方程我们并不能直接得到什么。
注意到小球速率的减小来源于重力做功,考虑动能定理(机械能守恒定律),选取点 A 所在水平面为势能零点,考虑小球正好抵达与圆心等高处的临界初速度,此时 $\theta=\frac{\pi }{2}~, cos \theta=0~,$
则:
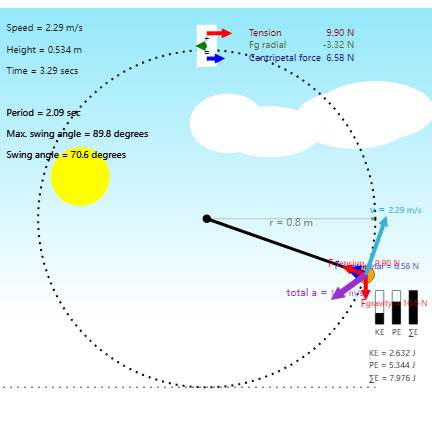
此即临界速度值,注意到初速度 $ \boldsymbol{\mathbf{v}} _0$ 不变时,其仅与轨迹半径 $R$(也即绳子长度)有关。当小球初速度小于该值时,小球在不超过圆心等高处的部分圆弧内做往返运,如图所示:
随着时间流逝,小球在接近与圆心等高处的同时速率逐渐减小至 0,进而反向加速:
4. 绳模型可能运动 2-向心脱轨,斜抛运动
求出 $ \boldsymbol{\mathbf{v}} _1$ 之后,我们自然想到另一个问题:若小球初速度稍大于 $ \boldsymbol{\mathbf{v}} _1$,它的运动状况又当如何呢?
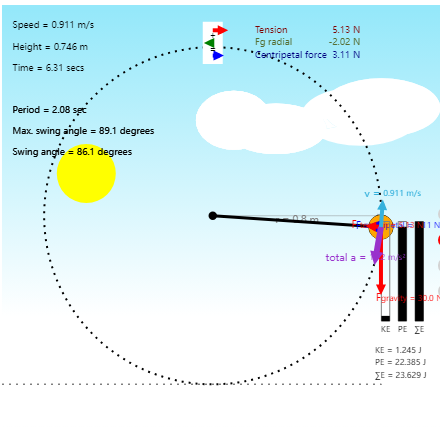
可以想象,存在一个速度临界值 $ \boldsymbol{\mathbf{v}} _3$,使得初速度超出该值的小球可以越过圆形轨迹最高处并做完完整的圆周运动,但对于介于 $ \boldsymbol{\mathbf{v}} _1$ 和 $ \boldsymbol{\mathbf{v}} _3$ 之间的初速度值,情况又当如何呢?小球是否会在上半圆弧中的某处绳拉力归零,且合力为重力,合加速度完全竖直向下呢?此时进行受力分析,小球在某个初始点只受重力且初速度非零,应当做抛体运动,且事实上是斜抛运动。
无疑,对于超出圆心等高处的上半圆弧,小球是可能脱离轨迹的,因为此时重力的向心分力有使小球脱离轨迹的趋势。
接下来,让我们对一个具体的物理情境考虑小球脱离轨迹的具体位置及相应的速率。