超对称性
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译)
在粒子物理学中,超对称性(SUSY)是一个原理,它提出了基本粒子之间两种基本类别的关系:玻色子具有整数值自旋和费米子具有半整数自旋。[1][2] 超对称性是时空对称的一种类型,是未被发现的粒子物理学的一个可能的候选者,如果被证实是正确的,它被认为是当前粒子物理学中许多问题的一个优秀的解决方案,可以解决当前理论被认为是不完整的各个领域。对标准模型的超对称扩展将通过保证扰动理论中所有阶的二次发散被抵消来解决规范理论中的主要层次问题。
在超对称性中,来自一组中的每一个粒子在另一组中都有一个关联的粒子,称为它的超对称伙伴,其自旋相差半个整数。这些超对称伙伴将是新的未被发现的粒子。例如,有一种粒子叫做 “超电子”(超伙伴电子),是电子的玻色子伙伴。在最简单的超对称性理论中,由于完美的 “不间断” 超对称性,每对超对称伙伴有相同的质量和内部量子数。因为我们希望用现在的设备找到这些 “超对称伙伴”,如果超对称性存在,那么它由自发破缺的对称性组成,允许超对称伙伴在质量上有所不同。[3][4][5] 自发破缺超对称性可以解决粒子物理中的许多神秘问题,包括等级问题。
目前没有证据表明超对称性是否正确,或者对当前模型的其他扩展可能更准确。从某种程度上说,这是因为自大约 2010 年,专门为研究标准模型之外的物理而设计的粒子加速器才开始运行,而且还不知道具体在哪里寻找,也不知道成功搜索所需的能量。
物理学家支持超对称性的主要原因是,目前的理论已知是不完整的,而且它们的局限性是公认的,超对称性将是一些主要问题的有吸引力的解决方案。直接确认将需要在对撞机实验中生产超对称伙伴,例如大型强子对撞机(LHC)。大型强子对撞机(LHC)的第一次运行除了希格斯玻色子之外没有发现以前未知的粒子,希格斯玻色子已经被怀疑是标准模型的一部分,因此也没有超对称性的证据。[6][7] 间接方法包括在已知的标准模型粒子中寻找永久电偶极矩(EDM),这可能发生在标准模型粒子与超对称粒子相互作用时。目前对电子电偶极矩的最佳约束是使其小于 10-28 e cm,相当于对 TeV 标度下新物理的灵敏度,与目前最好的粒子对撞机匹配。[8] 任何基本粒子中的永久电偶极矩都指向违反时间反转的物理现象,因此由 CPT 定理指向 CP 不对称性。这种电偶极矩实验也比传统的粒子加速器具有更大的可扩展性,并且随着加速器实验变得越来越昂贵和维护起来越来越复杂,它为检测超出标准模型的物理成分提供了一种实用的替代方法。
这些发现让许多物理学家失望,他们认为超对称性(以及其他依赖它的理论)是迄今为止 “新” 物理学最有希望的理论,并希望这些实验能有意想不到的结果。[9][10] 前热情支持者米哈伊尔·希夫曼(Mikhail Shifman)甚至敦促理论界寻找新的想法,并接受超对称性是一个失败的理论。[11] 然而,也有人认为这种 “自然” 危机还为时过早,因为各种计算对质量极限过于乐观,而质量极限将得到基于超对称性的解决方案。[12][13]
1. 动机
超对称性在电弱尺度附近有许多现象学动机,以及任何尺度的超对称性的技术动机。
1.1 等级问题
接近电弱尺度的超对称性改善了困扰标准模型的等级问题。[14] 在标准模型中,电弱尺度得到巨大的普朗克尺度量子修正。观察到的弱电标度和普朗克标度之间的等级必须通过非常精细的调谐来实现。另一方面,在超对称理论中,在伙伴和超伙伴之间的普朗克尺度的量子校正相互抵消(由于费米子环有负号)。弱电标度和普朗克标度之间的等级是以自然的方式实现的,没有奇迹般的调谐。
1.2 规范耦合统一
规范对称群在高能量时统一的观点被称为大统一理论。然而,在标准模型中,弱耦合、强耦合和电磁耦合在高能量时无法统一。在超对称理论中,对规范耦合的运行进行修改,实现了规范耦合的精确高能量统一。这种改进的运行也为辐射电弱对称性破缺提供了一种自然机制。
1.3 暗物质
TeV 尺度的超对称性(用离散对称性增强)通常以与热遗迹丰度计算一致的质量尺度提供候选暗物质粒子。[15][16]
1.4 其他技术动机
超对称性也是由几个理论问题的解决方案驱动的,这些解决方案通常提供许多理想的数学性质,并确保在高能量下的合理行为。超对称量子场论通常更容易分析,因为更多的问题在数学上变得容易处理。当超对称性被强加为局部对称性时,爱因斯坦的广义相对论被自动包含在内,其结果被称为超重力理论。这也是万物理论、超弦理论和 SUSY 理论中最受欢迎的候选者的一个必要特征,它可以解释宇宙膨胀的问题。
超对称性的另一个在理论上吸引人的特性是,它为科尔曼-满都拉定理(Coleman–Mandula)提供了唯一的 “漏洞”,该定理禁止时空和内部对称性以任何非平凡的方式结合,因为像标准模型这样的量子场理论都具有非常一般假设。哈格-奥普萨斯基-索赫纽斯(Haag–Łopuszański–Sohnius)定理证明了超对称性是时空和内部对称性能够一致结合的唯一方式。[17]
2. 历史
在强子物理学的背景下,宫泽弘毅(Hironari Miyazawa)于 1966 年首次提出了介子和重子之间的超对称性。这种超对称性不涉及时空,也就是说,它与内部对称性有关,并且被严重破坏。宫泽的工作在当时很大程度上被忽视了。[18][19][20][21]
J. L. Gervais 和 B. Sakita(在 1971 年),[22] Yu. A. Golfand 和 E. P. Likhtman(也是在 1971 年)和 D. V. Volkov 和 V. P. Akulov (1972 年),[23] 在量子场论的背景下独立地重新发现了超对称性,这是时空和基本场的一种全新类型的对称性,它建立了不同量子性质的基本粒子、玻色子和费米子之间的关系,并统一了时空和微观现象的内部对称性。1971 年,皮埃尔·雷蒙(Pierre Ramond)、约翰·施瓦兹(John H. Schwarz)和安德烈·奈芙(André Neveu)在弦论早期版本的背景下,首次出现了超对称性,这种超对称性具有一致的李代数分级结构,[24] 而热尔维斯·萨基塔(Gervais−Sakita)再发现正是基于这种结构。
最后,朱利叶斯·韦斯(Julius Wess)和布鲁诺·祖米诺(Bruno Zumino)(1974 年)[25] 确定了四维超对称场论的特征重整化特征,并将其定义为显著的量子场论,并且他们和阿卜杜勒·萨拉姆(Abdus Salam)及其同事介绍了早期粒子物理学的应用。超对称性的数学结构(分级李超代数)随后被成功地应用于其他物理课题,从核物理、[26][27] 临界现象、[28] 量子力学到统计物理。它仍然是许多物理学理论的重要组成部分。
标准模型的第一个现实超对称版本是由皮埃尔·费耶特(Pierre Fayet)在 1977 年提出的,被称为最小超对称标准模型,简称 MSSM。它的目的之一是解决等级问题。
3. 应用
3.1 可能对称群的扩展
物理学家探索超对称性的一个原因是,它为量子场论中更常见的对称性提供了一个延伸。这些对称性分为庞加莱(Poincaré)群和内对称性,并且科尔曼-满都拉(Coleman–Mandula)定理表明,在某些假设下,S 矩阵的对称性必须是具有紧内对称群的庞加莱(Poincaré)群的直接乘积,或者如果没有任何质量间隙,则是具有紧内对称群的共行群的直接乘积。1971 年,高尔夫(Golfand)和利赫曼(Likhtman)首次证明庞加莱(Poincaré)代数可以通过引入四个反交换自旋发生器(四维)来扩展,这后来被称为超电荷。1975 年,哈格-洛佩斯赞斯基-索赫纽斯(Haag–Lopuszanski–Sohnius)定理分析了所有可能的一般形式的超代数,包括那些具有大量超发生器和中心电荷的超代数。这个扩展的超庞加莱(Poincaré)代数为获得一大类非常重要的超对称场论铺平了道路。
超对称性代数
传统的物理学的对称性是由庞加莱(Poincaré)群的张量表示和内部对称性转换的物体产生的。然而,超对称性是由通过自旋表示变换的物体产生的。根据自旋统计定理,玻色子场交换而费米子场反交换。将这两种场组合成一个代数需要引入 $Z_2$ 分级,在 $Z_2$ 分级下玻色子是偶元素,费米子是奇元素。这样的代数叫做李超代数。
庞加莱(Poincaré)代数最简单的超对称扩展是超庞加莱(Poincaré)代数。用两个 Weyl 自旋表示,具有以下反交换关系: $${Q_\alpha, \overline{Q}_{\dot{\beta}}} = 2 (\sigma^\mu)_{\alpha \dot{\beta}} P_\mu~$$ $Qs$ 之间的所有其他反交换关系以及 $Qs$ 和 $Ps$ 之间的交换关系都消失了。在上面的表达式中 $\mathbf{P}_\mu = -i \partial_\mu$ 是变换生成器和 $\sigma^\mu$ 的 Pauli 矩阵。 存在李超代数的表示类似于李代数的表示。每个李代数都有一个相关的李群,李超代数有时可以推广到李超群的表示中。
3.2 超对称标准模型
将超对称性纳入标准模型需要将粒子数量加倍,因为标准模型中的任何粒子都不可能是彼此的超伙伴。随着新粒子的加入,可能会有许多新相互作用。与标准模型一致的最简单的可能超对称模型是最小超对称标准模型(MSSM),它可以包括能够成为标准模型中的超伙伴的必要的附加的新粒子。
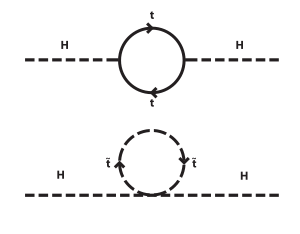
SUSY 的主要动机之一是对希格斯(Higgs)质量平方的二次发散贡献。希格斯玻色子的量子力学相互作用导致希格斯质量的大规模重整化,除非有偶然的抵消,希格斯质量的自然大小是最大可能的尺度。这个问题被称为等级问题。超对称性通过费米子和玻色子希格斯相互作用之间的自动抵消减小了量子修正的大小。如果超对称性在弱尺度下恢复,那么希格斯质量与超对称性破缺有关,超对称性破缺可以由解释弱相互作用和重力相互作用中极不相同尺度的小的非微扰效应引起。
在许多超对称标准模型中,有一个重稳定粒子(如中性子),它可以作为弱相互作用的大质量粒子(WIMP)暗物质候选者。超对称暗物质候选者的存在与 R 宇称密切相关。
将超对称性纳入现实理论的标准范式是使该理论的基本动力学超对称,但该理论的基态不遵守对称性,超对称性自发破裂。超对称性破缺不能像现在这样被 MSSM 粒子永久性地进行。这意味着理论中有一个新的领域负责这一突破。这个新领域的唯一限制是它必须永久打破超对称性,并且必须给出超粒子 TeV 尺度的质量。有许多模型可以做到这一点,它们的大部分细节都无关紧要。为了参数化超对称性破缺的相关特征,任意软 SUSY 破缺项被添加到暂时明确破缺 SUSY 的理论中,但绝不能从超对称性破缺的完整理论中产生。
规范耦合统一
超对称性存在的一个证据是规范耦合的统一。标准模型的三个规范耦合常数的重整化群演化对该理论的当前粒子含量有些敏感。如果我们使用标准模型运行重整化群,这些耦合常数在一个共同的能量尺度上并不完全一致。[29]结合最小 SUSY 后,耦合常数的联合收敛预计约为 $10^{16}$ GeV。[29]
3.3 超对称量子力学
超对称量子力学将 SUSY 超代数添加到量子力学中而不是量子场论。超对称量子力学在研究超对称孤子的动力学时经常变得很重要,并且由于具有仅仅是时间(而不是空间-时间)函数的场的简化性质,在这个主题上已经取得了很大的进展,并且现在正对其进行研究。
SUSY 量子力学涉及共享特定数学关系的哈密顿对,称为伙伴哈密顿量。(哈密顿量中出现的势能项称为伙伴势。)一个引论定理表明,对于一个哈密顿量的每个特征态,它的伙伴哈密顿量都有一个具有相同能量的相应特征态。这个事实可以用来推导特征态谱的许多性质。它类似于 SUSY 的最初描述,即玻色子和费米子。我们可以想象一个 “玻色子哈密顿量”,它的特征态是我们理论中的各种玻色子。这个哈密顿量的 SUSY 伙伴将是 “费米子”,它的特征态将是理论的费米子。每个玻色子都有一个能量相等的费米子伙伴。
3.4 凝聚态物理中的超对称性
SUSY 概念为 WKB 近似提供了有用的扩展。此外,SUSY 已经应用于量子和非量子无序平均系统(通过统计力学),福克-普朗克(Fokker-Planck)方程是非量子理论的一个例子。所有这些系统中的 “超对称性” 源于这样一个事实,即一个人正在模拟一个粒子,因此 “统计” 并不重要。超对称性方法的使用为复制技巧提供了一个数学上严格的替代方法,但仅在非交互系统中,这种方法试图解决无序平均下所谓的 “分母问题”。更多关于超对称性在凝聚态物理学中的应用,请参见伊夫托夫(1997)。[30]
3.5 光学中的超对称性
最近发现集成光学[31]提供了一个肥沃的土壤,可以在容易接近的实验室环境中探索 SUSY 的某些分支。利用量子力学薛定谔方程的类似数学结构和控制一维光演化的波动方程,我们可以将结构的折射率分布解释为光波包在传播的潜在景观。以这种方式,一类新的功能光学结构就有可能在相位匹配、模式转换[32] 和空分复用系统中应用。SUSY 变换也被提出作为解决光学中逆散射问题和一维变换光学的一种方法。[33]
3.6 动力系统中的超对称性
所有随机(偏)微分方程,即所有连续时间动力系统的模型,都具有拓扑超对称性。[34][35] 在随机演化的算子表示中,拓扑超对称性是与随机演化算子交换的外部导数,该算子定义为由 SDE 定义的相空间的微分同胚在微分形式上诱导的随机平均回撤。新兴的超对称随机动力学理论的拓扑扇区可以被认为是威滕(Witten)型拓扑场论。
动态系统中拓扑超对称性的意义是保持相空间连续性——即使在有噪声的情况下,在连续时间演化过程中,无限闭合点仍将保持闭合。当拓扑超对称性自发破裂时,这一性质在无限长时间演化的极限内被违反,可以说该模型表现出蝴蝶效应(的随机推广)。从更一般的角度来看,拓扑超对称性的自发破裂是普遍存在的混沌、湍流、自组织临界性等动力学现象的理论本质。戈德斯通(Goldstone)定理解释了伴随出现的长期动力学行为,表现为 1/f 噪声、蝴蝶效应和突然(瞬时)过程的无标度统计,例如地震、神经雪崩、太阳耀斑等,被称为齐夫定律和里氏震级。
3.7 数学中的超对称性
有时也会从数学上研究 SUSY 的内在特性。这是因为它描述了满足全纯性质的复杂场,这允许精确计算全纯量。这使得超对称模型成为更现实的理论中有用的 “玩具模型”。一个典型的例子是四维规范理论中交换粒子和单极子的 S-对偶性的证明。[36]
利用超对称量子力学极大地简化了阿提亚辛格(Atiyah-Singer)指数定理的证明。
3.8 量子重力中的超对称性
超对称性是超弦理论的一部分,超弦理论是量子引力的弦理论,尽管理论上它也可以是其他量子引力理论的一个组成部分,例如环量子引力。为了使超弦理论保持一致,似乎在某种程度上需要超对称性(尽管它可能是一个强烈的破缺的对称性)。如果实验证据证实超对称性的形式为超对称粒子,比如通常中性伴子被认为是最轻的超伴子,一些人认为这将是对超弦理论的重大推动。由于超对称性是超弦理论的必要组成部分,任何发现的超对称性都将与超弦理论相一致。如果大型强子对撞机和其他主要粒子物理实验未能探测到超对称伙伴,许多版本的已经预测到现有粒子的某些低质量超伙伴的超弦理论可能需要进行重大修正。
4. 一般超对称性
超对称性出现在许多理论物理学的相关领域中。它有可能有多个超对称性,也有超对称性的额外维度。
4.1 扩展超对称性
有可能有多种的超对称性变换。具有一个以上超对称性变换的理论被称为扩展超对称理论。理论的超对称性越强,场的内容和相互作用受到的约束越大。通常,超对称性的拷贝数是 2 的幂,即 1,2,4,8。在四维空间中,自旋器有四个自由度,因此超对称性发生器的最小数量是四维空间中的四个,并且有八个超对称性副本意味着有 32 个超对称性发生器。
超对称发生器的最大可能数量是 32 个。具有 32 个以上超对称发生器的理论自动具有自旋大于 2 的无质量场。还不知道如何使自旋大于两个的无质量场相互作用,所以所考虑的最大超对称发生器数量是 32 个。这归因于温伯格-威滕(Weinberg-Witten)定理。这相当于一个 N = 8 的超对称性理论。有 32 个超对称性的理论自动有引力子。
对于四维空间,有以下理论,以及相应的多重态[37] (只要在这种对称性下它们不是不变的,CPT 就添加一个副本)
- $N = 1$
- 手性多重态:(0,1⁄2)
- 向量多重态: (1⁄2,1)
- 重力多重态:(1,3⁄2)
- 引力子多重态: (3⁄2,2)
- $N = 2$
- 超多重谱线:(-1⁄2,02,1⁄2)
- 向量多重态:(0,1⁄22,1)
- 超重力多重态:(1,3⁄22,2)
- $N = 4$
- 向量多重态:(-1,-1⁄24,06,1⁄24,1)
- 超重力多重态:(0,1⁄24,16,3⁄24,2)
- $N = 8$
- 超重力多重态:(-2,-3⁄28,-128,-1⁄256,070,1⁄256,128,3⁄28,2)
4.2 维数交替的超对称性
除了四维之外,其他维度还可能有超对称性。因为自旋子的性质在不同维度之间变化很大,所以每个维度都有其特征。在 d 维中,自旋的大小约为 2d/2 或 2(d − 1)/2。既然超对称的最大数量是 32,超对称理论可以存在的最大维数是 11。
4.3 分数超对称性
分数超对称性是超对称性概念的推广,其中最小正自旋量不一定是 1⁄2,但对于整数值 N 可以是任意的 1⁄N。这种推广在两个或更少的时空维度中是可能的。
5. 现状
超对称模型受到各种实验的限制,包括低能可观测值的测量——例如费米实验室中μ子的异常磁矩;WMAP 暗物质密度测量和直接探测实验——例如氙-100 和 LUX;并通过粒子对撞机实验,包括 B 衰变,希格斯现象学和在大型正负电子对撞机、万亿电子伏加速器和大型强子对撞机上直接搜索超伙伴(超粒子)。
历史上,最严格的限制来自对撞机的直接生产。在欧洲核子研究中心,通过在超级质子同步加速器进行的 UA1 实验和 UA2 实验,首次确定了超对称夸克和胶子的质量极限。LEP 后来设定了非常严格的限制,[38] 2006 年,Tevatron 的 D0 实验扩展了这一限制。[39][40] 从 2003 年到 2015 年,WMAP 和普朗克的暗物质密度测量很强的约束了超对称性模型,如果它们能解释暗物质,就必须进行调整,以调用特定的机制来充分降低中性子密度。
在 2009 年大型强子对撞机开始之前,CMSSM 和 NUHM1 的可用数据显示,夸克和胶子的质量最有可能在 500 至 800 千兆电子伏范围内,尽管允许高至 2.5 千兆电子伏但概率较低。中性子和超轻子被认为相当轻,最轻的中性子和最轻的 stau 最有可能在 100 到 150 GeV 之间找到。[41]
LHC 的第一次运行没有发现超对称性的证据,因此,超过了大型正负电子对撞机和万亿电子伏加速器现有的实验极限,部分排除了上述预期范围。[42]
2011-2012 年,LHC 发现了质量约为 125 千兆瓦的希格斯玻色子,并与符合标准模型的费米子和玻色子耦合。MSSM 预言最轻希格斯玻色子的质量不应该比 Z 玻色子的质量高得多,并且在没有微调的情况下(超对称性破缺标度在 1 TeV 的数量级),不应该超过 135 GeV。[43]
对于最小超对称模型来说,LHC 结果似乎是有问题的,因为 125 GeV 的值对于该模型来说相对较大,并且只能通过来自顶方夸克的大辐射环校正来实现,许多理论家认为这是 “非自然的”。[44]
6. 参考文献
[1] ^Haber, Howie. "SUPERSYMMETRY, PART I (THEORY)" (PDF). Reviews, Tables and Plots. Particle Data Group (PDG). Retrieved 8 July 2015..
[2] ^"supersymmetry". Merriam-Webster. Retrieved October 2, 2017..
[3] ^Martin, Stephen P. (1997). "A Supersymmetry Primer". Perspectives on Supersymmetry. Advanced Series on Directions in High Energy Physics. 18. pp. 1–98. arXiv:hep-ph/9709356. doi:10.1142/9789812839657_0001. ISBN 978-981-02-3553-6..
[4] ^Baer, Howard; Tata, Xerxes (2006). Weak scale supersymmetry: From superfields to scattering events..
[5] ^Dine, Michael (2007). Supersymmetry and String Theory: Beyond the Standard Model. p. 169..
[6] ^"ATLAS Supersymmetry Public Results". ATLAS, CERN. Retrieved 2017-09-24..
[7] ^"CMS Supersymmetry Public Results". CMS, CERN. Retrieved 2017-09-24..
[8] ^Baron, J.; Campbell, W. C.; Demille, D.; Doyle, J. M.; Gabrielse, G.; Gurevich, Y. V.; Hess, P. W.; Hutzler, N. R.; Kirilov, E.; Kozyryev, I.; O'Leary, B. R.; Panda, C. D.; Parsons, M. F.; Petrik, E. S.; Spaun, B.; Vutha, A. C.; West, A. D.; West, A. D. (2014). "Order of Magnitude Smaller Limit on the Electric Dipole Moment of the Electron". Science. 343 (6168): 269–272. arXiv:1310.7534. doi:10.1126/science.1248213. PMID 24356114..
[9] ^Wolchover, Natalie (November 20, 2012). "Supersymmetry Fails Test, Forcing Physics to Seek New Ideas". Quanta Magazine..
[10] ^Wolchover, Natalie (August 9, 2016). "What No New Particles Means for Physics". Quanta Magazine..
[11] ^M. Shifman: Reflections and Impressionistic Portrait at the Conference Frontiers Beyond the Standard Model, FTPI (pdf), FTPI, 31 October 2012. [12] ^Howard Baer; Vernon Barger; Dan Mickelson (September 2013). "How conventional measures overestimate electroweak fine-tuning in supersymmetric theory". Physical Review D. 88 (9): 095013. arXiv:1309.2984. Bibcode:2013PhRvD..88i5013B. doi:10.1103/PhysRevD.88.095013..
[13] ^Howard Baer; et al. (December 2012). "Radiative natural supersymmetry: Reconciling electroweak fine-tuning and the Higgs boson mass". Physical Review D. 87 (11): 115028. arXiv:1212.2655. Bibcode:2013PhRvD..87k5028B. doi:10.1103/PhysRevD.87.115028..
[14] ^David, Curtin (August 2011). "MODEL BUILDING AND COLLIDER PHYSICS ABOVE THE WEAK SCAE" (PDF) (COLLIDER PHYSICS ABOVE THE WEAK SCALE)..
[15] ^Jonathan Feng: Supersymmetric Dark Matter (pdf), University of California, Irvine, 11 May 2007.
[16] ^Torsten Bringmann: The WIMP "Miracle" (pdf) Archived 2013-03-01 at the Wayback Machine University of Hamburg.
[17] ^R. Haag, J. T. Łopuszański and M. Sohnius, "All Possible Generators Of Supersymmetries Of The S Matrix", Nucl. Phys. B 88 (1975) 257.
[18] ^H. Miyazawa (1966). "Baryon Number Changing Currents". Prog. Theor. Phys. 36 (6): 1266–1276. Bibcode:1966PThPh..36.1266M. doi:10.1143/PTP.36.1266..
[19] ^H. Miyazawa (1968). "Spinor Currents and Symmetries of Baryons and Mesons". Phys. Rev. 170 (5): 1586–1590. Bibcode:1968PhRv..170.1586M. doi:10.1103/PhysRev.170.1586..
[20] ^Michio Kaku, Quantum Field Theory, ISBN 0-19-509158-2, pg 663..
[21] ^Peter Freund, Introduction to Supersymmetry, ISBN 0-521-35675-X, pages 26-27, 138..
[22] ^Gervais, J.-L.; Sakita, B. (1971). "Field theory interpretation of supergauges in dual models". Nuclear Physics B. 34 (2): 632–639. Bibcode:1971NuPhB..34..632G. doi:10.1016/0550-3213(71)90351-8..
[23] ^D. V. Volkov, V. P. Akulov, Pisma Zh.Eksp.Teor.Fiz. 16 (1972) 621; Phys.Lett. B46 (1973) 109; V.P. Akulov, D.V. Volkov, Teor.Mat.Fiz. 18 (1974) 39.
[24] ^Ramond, P. (1971). "Dual Theory for Free Fermions". Physical Review D. 3 (10): 2415–2418. Bibcode:1971PhRvD...3.2415R. doi:10.1103/PhysRevD.3.2415..
[25] ^Wess, J.; Zumino, B. (1974). "Supergauge transformations in four dimensions". Nuclear Physics B (Submitted manuscript). 70 (1): 39–50. Bibcode:1974NuPhB..70...39W. doi:10.1016/0550-3213(74)90355-1..
[26] ^Hagen Kleinert, Discovery of Supersymmetry in Nuclei.
[27] ^Iachello, F. (1980). "Dynamical Supersymmetries in Nuclei". Physical Review Letters. 44 (12): 772–775. Bibcode:1980PhRvL..44..772I. doi:10.1103/PhysRevLett.44.772..
[28] ^Friedan, D.; Qiu, Z.; Shenker, S. (1984). "Conformal Invariance, Unitarity, and Critical Exponents in Two Dimensions". Physical Review Letters. 52 (18): 1575–1578. Bibcode:1984PhRvL..52.1575F. doi:10.1103/PhysRevLett.52.1575..
[29] ^Gordon L. Kane, The Dawn of Physics Beyond the Standard Model, Scientific American, June 2003, page 60 and The frontiers of physics, special edition, Vol 15, #3, page 8.
[30] ^Supersymmetry in Disorder and Chaos, Konstantin Efetov, Cambridge University Press, 1997..
[31] ^Miri, M.-A.; Heinrich, M.; El-Ganainy, R.; Christodoulides, D. N. (2013). "Superymmetric optical structures". Physical Review Letters. 110 (23): 233902. arXiv:1304.6646. Bibcode:2013PhRvL.110w3902M. doi:10.1103/PhysRevLett.110.233902. PMID 25167493..
[32] ^Heinrich, M.; Miri, M.-A.; Stützer, S.; El-Ganainy, R.; Nolte, S.; Szameit, A.; Christodoulides, D. N. (2014). "Superymmetric mode converters". Nature Communications. 5: 3698. arXiv:1401.5734. Bibcode:2014NatCo...5E3698H. doi:10.1038/ncomms4698. PMID 24739256..
[33] ^Miri, M.-A.; Heinrich, Matthias; Christodoulides, D. N. (2014). "SUSY-inspired one-dimensional transformation optics". Optica. 1 (2): 89–95. arXiv:1408.0832. doi:10.1364/OPTICA.1.000089. Retrieved August 6, 2014..
[34] ^Ovchinnikov, Igor (March 2016). "Introduction to Supersymmetric Theory of Stochastics". Entropy. 18 (4): 108. arXiv:1511.03393. Bibcode:2016Entrp..18..108O. doi:10.3390/e18040108..
[35] ^Ovchinnikov, Igor; Ensslin, Torsten (April 2016). "Kinematic dynamo, supersymmetry breaking, and chaos". Physical Review D. 93 (8): 085023. arXiv:1512.01651. Bibcode:2016PhRvD..93h5023O. doi:10.1103/PhysRevD.93.085023..
[36] ^Krasnitz, Michael (2003). Correlation functions in supersymmetric gauge theories from supergravity fluctuations (PDF). Princeton University Department of Physics: Princeton University Department of Physics. p. 91..
[37] ^Polchinski,J. String theory. Vol. 2: Superstring theory and beyond, Appendix B.
[38] ^LEPSUSYWG, ALEPH, DELPHI, L3 and OPAL experiments, charginos, large m0 LEPSUSYWG/01-03.1.
[39] ^The D0-Collaboration (2009). "Search for associated production of charginos and neutralinos in the trilepton final state using 2.3 fb−1 of data". Physics Letters B. 680 (1): 34–43. arXiv:0901.0646. Bibcode:2009PhLB..680...34D. doi:10.1016/j.physletb.2009.08.011. hdl:10211.3/195394..
[40] ^The D0 Collaboration (2008). "Search for squarks and gluinos in events with jets and missing transverse energy using 2.1 fb-1 of pp¯ collision data at s=1.96 TeV". Physics Letters B. 660 (5): 449–457. arXiv:0712.3805. Bibcode:2008PhLB..660..449D. doi:10.1016/j.physletb.2008.01.042..
[41] ^O. Buchmueller; et al. (2009). "Likelihood Functions for Supersymmetric Observables in Frequentist Analyses of the CMSSM and NUHM1". The European Physical Journal C. 64 (3): 391–415. arXiv:0907.5568. Bibcode:2009EPJC...64..391B. doi:10.1140/epjc/s10052-009-1159-z..
[42] ^Roszkowski, Leszek; Sessolo, Enrico Maria; Williams, Andrew J. (11 August 2014). "What next for the CMSSM and the NUHM: improved prospects for superpartner and dark matter detection". Journal of High Energy Physics. 2014 (8): 67. arXiv:1405.4289. Bibcode:2014JHEP...08..067R. doi:10.1007/JHEP08(2014)067..
[43] ^Marcela Carena and Howard E. Haber; Haber (2003). "Higgs Boson Theory and Phenomenology". Progress in Particle and Nuclear Physics. 50 (1): 63–152. arXiv:hep-ph/0208209. Bibcode:2003PrPNP..50...63C. doi:10.1016/S0146-6410(02)00177-1..
[44] ^Draper, Patrick; et al. (December 2011). "Implications of a 125 GeV Higgs for the MSSM and Low-Scale SUSY Breaking". Physical Review D. 85 (9): 095007. arXiv:1112.3068. Bibcode:2012PhRvD..85i5007D. doi:10.1103/PhysRevD.85.095007..