浮力、阿基米德原理（初中）

贡献者： addis

预备知识　液体中的压强、连通器

1. 物体完全浸没的浮力

　　¹我们先用一个简单易懂的方式解释浮力。假设在重力加速度为 $g$ 的环境中，容器中密度为 $\rho_0$ 的液体完全静止。这时令液体内部有一任意形状的闭合曲面，体积为 $V_0$。

图 1：浮力就是液体（或其他流体）对物体表面的压力的合力

　　把曲面内部的液体作为一个整体做受力分析，其质量为 $m = \rho_0 V_0$，所受重力为 $mg = \rho_0 V_0 g$。由于曲面中液体保持静止，说明曲面外的液体对曲面内的液体施加的合力与它的重力等大反向，这个力就是浮力（buoyancy）。现在我们如果把曲面内的液体替换为一个表面光滑的其他物体，由于曲面形状不改变，外界液体对该物体的浮力仍然为

\begin{equation} F = \rho_0 V_0 g~. \end{equation}

这就是所谓的 “物体所受的浮力等于它排开液体的重力”。为什么要说 $V_0$ 是 “排开水的体积” 而不直接说是 “物体的体积” 呢？当物体完全浸没在水中时，二者的确是相等的，但下文我们还会讨论物体只有部分浸没的情况，此时二者就不相等。

　　虽然我们上面习惯性地使用 “水” 或 “液体” 这个词，但任何流体中的物体都可能受到浮力。例如氢气球或热气球上升就是因为在空气中受到了浮力。此时 $\rho_0$ 就是空气的密度。

　　为什么把水替换成物体后表面各点受到的压力不变呢？物体表面任意一点受到的水压仅取决于深度，水是 “看不见” 物体内部有什么的。

　　既然浮力与物体的材料无关，为什么同样形状的物体有的会在水中上浮而有的却下沉呢？这是因为物体的上浮或下沉取决于物体受到的合力，也就是物体受到的所有力的叠加。在这里物体除了受浮力还受重力，而重力是物体的材料和体积共同决定的。当重力大于浮力，合力向下，所以下沉。反之则上浮。所以再次强调浮力不包括重力，与物体的材质无关。

　　若物体的密度恒定，那么它所受的重力大小就是

\begin{equation} G = mg = \rho V g~. \end{equation}

其中 $m, V, \rho$ 分别是物体的质量、体积和密度。物体完全浸没时有 $V = V_0$。对比式 1 我们会发现当物体密度等于水的密度时（$\rho = \rho_0$），$G = F$，也就是合力为零，这代表物体可以静止在水中。当 $\rho < \rho_0$ 时 $G < F$，合力向上，物体会上浮。当 $\rho > \rho_0$ 时 $G > F$，合力向下，物体下沉。

2. 只有重力能产生浮力吗？

　　现在考虑一个问题：只有重力或者说万有引力会导致浮力吗？在浮力公式式 1 中，$g$ 是重力加速度，于是你可能会反问 “没有重力哪来的重力加速度？”。但事实上我们在推导浮力公式的过程中并不要求液体受到的力一定是万有引力，而是只要液体均匀地受到某个方向的合力，就会产生在反方向的浮力。

　　如果我们在电梯中做浮力实验，当电梯加速上升时会有一种叫做 “超重” 的现象。此时如果在容器下方放一个体重秤，那么会发现称的读数增加了。这说明单位体积的液体似乎受到了额外的向下的力²。那么仍然使用上面的等效法计算浮力，此时式 1 就不再有效，而是需要把 $g$ 替换为一个更大的数 $a$。例如如果秤的读数变为两倍，则 $a = 2g$。反之，如果电梯向下加速，那么会出现 “失重”，也就是秤的读数会变小，那么我们将需要令 $a < g$。如果电梯向下加速的速度非常大，以至于完全失重（秤的读数变为零），那么浮力也将随着消失。如果电梯具有更大的向下加速度，那么人将可以站在电梯的天花板上，此时浮力的方向也将指向下。

　　另一种有趣的情况是在一个加速形势的车中，所有的物体都会受到和加速方向相反的惯性力，也包括容器中的液体。所以当车加速时，液体所受的水平惯性力和重力叠加后将不再竖直向下而是斜向下。此时液体表面的倾斜正是说明了这一点。这时等效法的分析仍然有效：水中物体所受的浮力将同样倾斜，也就是垂直于水面指向向斜上方。

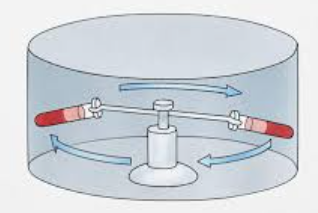
　　离心机正是运用了这个原理，使容器中的液体获得巨大的离心力，从而产生巨大的浮力，使物体中密度较小的固体或其他液体向旋转中心 “上” 浮。

图 2：离心机的原理

3. 物体露出水面的浮力

图 3：物体露出水面时的浮力，左右两个物体浮力相等

　　如果物体只有部分在水中，则情况会更复杂一些。若水的外部为真空，那么物体表面在水面之外的部分不受任何压强。于是我们可以等效认为物体露出水面的部分不存在。这样就可以使用上文的等效方法计算浮力了。所以使用式 1 计算该物体浮力时，$V_0$ 应该仍然是物体排开水的体积而不是物体自身的体积。

未完成：但一般来说，物体表面在水面之外的部分仍然会受到大气压强，为什么不需要考虑？答案：若忽略空气密度，增加一个大气压使得物体表面各点的压强增加相同，互相抵消。若不忽略，可以把物体看成两部分分别计算浮力。

4. 直接计算浮力

　　由于我们还没有学习微积分，只能计算一些非常简单的例子。

例 1　柱体的浮力

　　柱体的浮力容易通过简单的压强计算获得。例如一个边长为 $L$ 的立方体完全浸泡在某种液体中，其四个侧面受到的压强都是沿水平方向的，且互相抵消，对浮力贡献为零。下表面受到向上的压强为 $P_1 = \rho g h_1$ 对浮力的贡献为 $F_1 = L^2 P_1$。同理，上表面受到向下的压强为 $P_2 = \rho g h_2$，对浮力的贡献为 $F_2 = -L^2 P_2$。所以总浮力为

\begin{equation} F = F_1 + F_2 = \rho g L^2 (h_1 - h_2) = \rho g L^3 = \rho g V~, \end{equation}

其中 $\rho$ 是液体的体积。对于其他柱体（如圆柱，三棱柱等），若竖直放置，同样可以通过以上方法得到式 1 。