伯努利方程
贡献者: addis; ACertainUser
- 本文缺少预备知识,初学者可能会遇到困难。
伯努利方程是关于不可压缩的流体的方程。1
假设液体不可被压缩、没有粘滞性、与管壁也没有摩擦阻力,那么处处满足伯努利方程
\begin{equation}
\frac{v^2}{2} + gz + \frac{p}{\rho} = \text{常数}~.
\end{equation}
可以根据伯努利原理设计液体测速计等设备。
推导
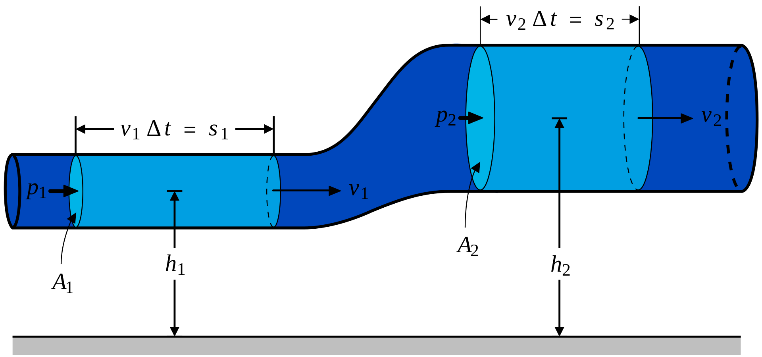
图 1:伯努利方程的推导 (参考相关页面)
2如图,一根管子的粗细不同两部分的横截面面积分别为 $A_1, A_2$,压强分别为 $p_1, p_2$,高度分别为 $h_1, h_2$;其中流过的液体密度为 $\rho$,管内流速分布不随时间变化,在 1,2 两处的速度分别为 $v_1, v_2$。
考虑 $A_1, A_2$ 之间的这段液体,假设一段 $\Delta t$ 时间内,起左端和右端分别移动了 $s_1, s_2$。 根据不可压缩的假设,流入水管的水量等于流出水管的水量,$A_1v_1\Delta t=A_2v_2\Delta t=V$,即 $m1=m2$。这个过程中这段液体的机械能改变了多少呢?机械能包括动能和重力势能。由于中间深蓝色的部分的机械能保持不变,所以可以等效视为 1 处的一小截液体移动到了 2 处。
浅蓝色的两段液体的机械能为
\begin{equation}
E_1=\frac{1}{2}mv_1^2+mgh_1, \qquad
E_2=\frac{1}{2}mv_2^2+mgh_2~,
\end{equation}
再考虑液体压力的做功。$A_1,A_2$ 之间的液体向右移动时,$A_1$ 处的压强对其做正功,$A_2$ 处的压强对其做负功。
\begin{equation}
W_1=p_1v_1A_1\Delta t=p_1V, \qquad
W_2=-p_2v_2A_2 \Delta t=-p_2V ~,
\end{equation}
\begin{equation}
p_1V+\frac{1}{2}mv_1^2+mgh_1=p_2V+\frac{1}{2}mv_2^2+mgh_2~.
\end{equation}
\begin{equation}
pV+\frac{1}{2}mv^2+mgh=\text{常数}~,
\end{equation}
\begin{equation}
\frac{p}{\rho} + \frac{v^2}{2} + gh = \text{常数}~.
\end{equation}
未完成:这样的推导如何拓展到开放空间的情况呢?举例:水龙头下的乒乓球,香蕉球,机翼,两张纸中间吹气