trie 树(字典树)
贡献者: 有机物
$\mathtt{Trie}$ 树(字典树)高效的存储和查找字符串集合的数据结构。
假设要存储这些字符串:
cat、her、him、no、nova。
对应在图上就长这样:
图 1:$\mathtt{trie}$ 树
插入字符串:从根结点开始看,看有没有这个字母,有的话就走,没有的话就创建一个新的字母结点。存储每个单词一般都会在这个单词的结尾字母打一个标记(如图中的蓝色结点),意思是以这个字母为结尾的路径是有一个单词的。插入一个字符串动图
查找字符串:比如要查找 him 这个单词,我们就从根结点开始走,依次走每个字母,如果找到了要查找的字符串的结尾字母并且这个结点上有标记,就表示找到了这个字符串。查找字符串动图
来看一个具体题目:维护一个字符串集合,支持两种操作:
-
I x向集合中插入一个字符串 x; -
Q x询问一个字符串在集合中出现了多少次。
共有 $N$ 个操作,输入的字符串总长度不超过 $10^5$,字符串仅包含小写英文字母。
样例:
输入: 输出:
11
I cat
Q cat 1
Q ca 0
I her
Q her 1
I him
Q him 1
I no
Q no 1
I nova
Q nova 1
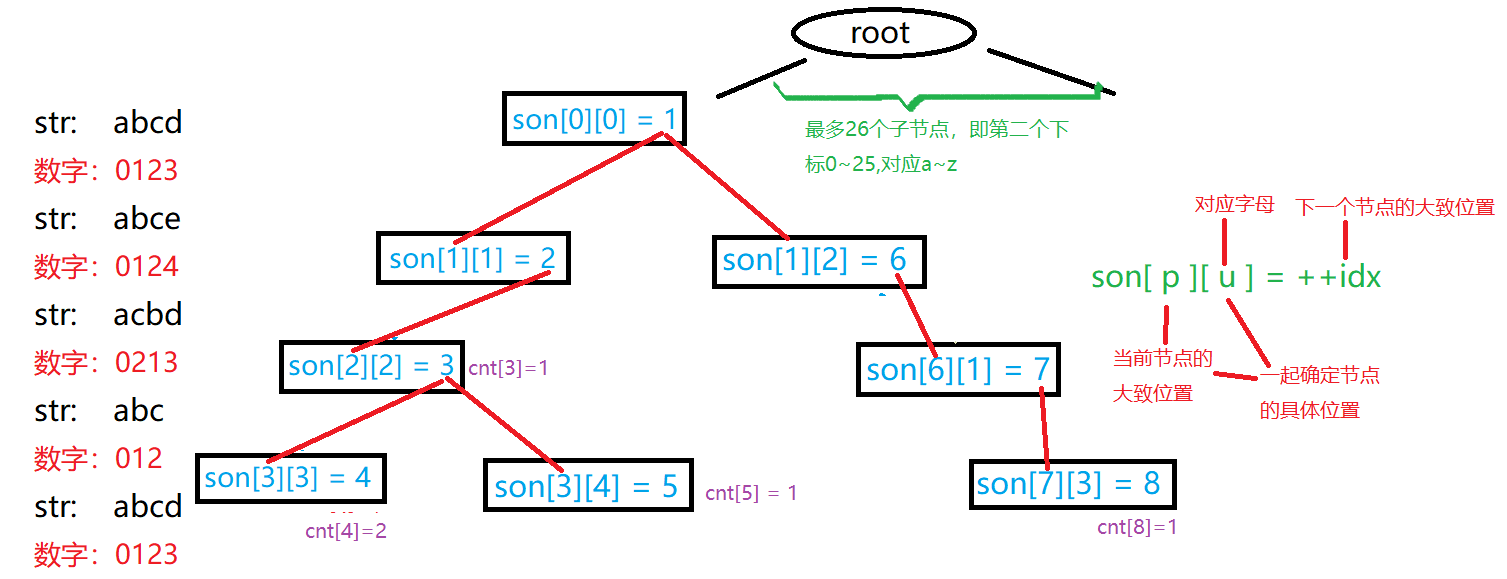
开一个数组 sno[N][26] 来表示每个点的所有儿子,第一维存储结点大小,第二维存储每个字母,因为字符串仅包含小写英文字母,所以第二维只开 $26$ 的大小就可以了。cnt[N] 表示以当前字母为结点的字母有多少个(标记)idx 的含义和链表里的 idx 含义一样。
图 2:数组模拟 $\mathtt{Trie}$ 树
// 插入(存储)字符串
void insert(string str)
{
int p = 0; // 类似指针,从根结点开始
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a'; // 'a' ~ 'z' 映射成 0 ~ 25
if (!son[p][u]) son[p][u] = ++ idx; // 该结点不存在,创建结点
p = son[p][u]; // 使 p 指向(走到)子结点
}
cnt[p] ++ ; // 以 p 结点为结尾的单词数量 ++
}
// 查询字符串出现的次数
int find(string str)
{
int p = 0;
for (int i = 0; str[i]; i ++ )
{
int u = str[i] - 'a';
if (!son[p][u]) return 0; // 没有的话就返回 0,表示这个字符串在集合中没有出现过
p = son[p][u]; // 有的话走向子结点
}
return cnt[p]; // 返回以 p 结点为结尾的单词数量
}