二叉树
贡献者: 有机物
每个节点最多含有两个子树的树被称为二叉树。
二叉树的特点:
- 每个结点只有两棵子树,分别为左子树和右子树;
- 二叉树的左右子树如果位置发生了改变,含义也会发生改变
不包含任意结点的二叉树称为空树或零树,如果左子树非空,则它的根称为整棵树的根的左孩子,右子树也类似。在一棵二叉树中,如果一个结点仅有一个孩子,则它是左孩子还是右孩子是有关系的。而在有序树中,则是一样的。
二叉树的性质:
在第 $i$ 层上最多有 $2 ^ {i - 1}$ 个节点。$(i\geq1)$
二叉树中深度为 $k$,那么最多有 $2 ^ {k - 1}$ 个节点。$(k\geq1)$,(根节点的深度为 $k_0 = 0$)。
满二叉树:
国内定义:满二叉树是指每层上的所有结点都有两个子结点的二叉树,最后一层的结点(叶结点)是满的,因此满二叉树形如一个三角形。一个层数为 $k$ 的满二叉树总结点数为 $2^k - 1$。$(k\geq1)$。
国外定义:如果二叉树的每个节点要么是叶结点,要么正好拥有两个子结点,那么就是一棵满二叉树。
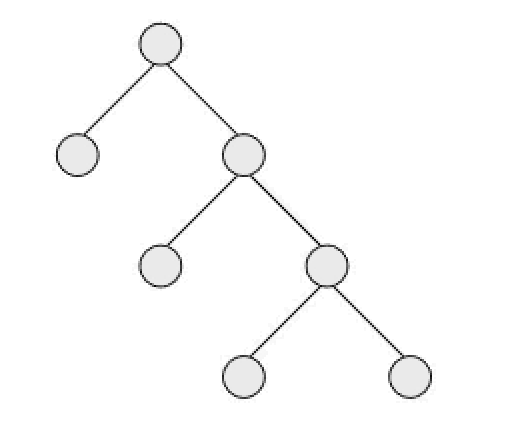
图 1:示例图
如上图在国内就不是一棵满二叉树,而在国外就是一棵满二叉树。
完全二叉树:
在一颗二叉树中,若除最后一层外的其余层都是满的,并且最后一层要么是满的,要么结点从左到右依次排列。