堆

贡献者：有机物

　　堆是一棵完全二叉树，且每个结点上的编号都不小于或不大于其父结点的编号，堆的结点上并没有权值。而二叉堆的结点上具有权值，且满足堆的性质。满足父结点不小于左右两个子结点的二叉堆被称为大根堆，反之为小根堆。大根堆与小根堆都被属于二叉堆。但是一般没有特别指出的堆一般都指二叉堆。

　　以一个例题来讲解堆。

　　维护一个集合，初始时集合为空，支持如下几种操作：

插入一个数 $x$；
输出当前集合中的最小值；
删除当前集合中的最小值；
删除第 $k$ 个插入的数；
修改第 $k$ 个插入的数，将其变为 $x$。

　　本题要我们实现一个小根堆，根结点是整课树中最小的结点，父结点永远小于等于左右两个子结点。 C++ STL 中的堆只能实现前 $3$ 个操作。

priority_queue<int, vector<int>, greater<int>> heap;   // 定义小根堆的方式
int t;
cin >> t;
while (t -- )
{
    int x;            
    cin >> x;
    heap.push(x);   // 向队尾插入一个数 x
    cout << heap.top() << endl;     // 输出最小值，即队头
    heap.pop();     // 删除最小值，即删除队头
}

　　要想实现随机删除和修改，只能用数组来模拟堆，所以我们讲解一下如何使用数组模拟堆。

　　首先需要一个数组 h[N] 用于存储堆中的元素，由于需要在任意位置进行删除和修改，所以需要多开两个数组 ph[N] 和 hp[N]。

　　 ph[i] 的意思是第 $i$ 个插入的数在堆中的下标是什么，而 hp[i] 的意思是在堆中下标是 $i$ 的点是第几个插入的。比如 ph[1] = a，hp[a] = 1。

　　因为是随机插入和删除，所以在堆中删除或者插入某个值的话必定要进行调整。分为 up 操作和 $down$ 操作，up 是如果一个数不符合堆的性质就要往上调整，$down$ 也同理，因为某个数不符合堆的性质，就要往下调整。

　　堆的存储只用开一个一维数组 h[N] 就可以了，父结点是 $i$，左子结点就是 $2 \times i$，右子结点就是 $2 \times i + 1$。 $2 \times i$ 可以写成 u << 1，$2 \times i + 1$ 可以写成 u << 1 | 1。比如父结点的下标是 $1$，左子结点的下标就是 $2$，右子结点的下标就是 $3$。有一点需要注意：下标必须从 $1$ 开始，如果从 $0$ 开始的话左子结点和右子结点的下标均为 $0$，这样显然是不行的。

　　插入一个数，就直接在堆的结尾插入一个数就可以了，然后再 up 一遍。

　　输出最小值直接输出堆顶，一定是最小值。

　　删除最小值直接删除堆顶不太好删，我们可以把堆的结尾的数与堆顶的数交换，再删除堆的结尾的数（交换完之后堆的结尾的数就是堆顶，即最小值）删除，然后再从根节点 down 一遍，这样就实现了删除最小值。

　　删除任意一个数与删除最小值类似，都是把堆的结尾的数与要删除的数交换，然后再删除堆的结尾的数，最后要注意进行 up 或 down 操作，为了不判断，干脆两个操作都写上，虽然两个函数都执行了，但其中只有一个函数对堆有影响。

　　修改任意一个数直接修改就好了，最后也要注意进行 up 或 down 操作。

　　 up 操作与 down 操作的时间复杂度都为 $\mathcal{O}(\log_2 n)$，输出最小值是 $\mathcal{O}(1)$ 的。所以除了输出最小值，其他操作的时间复杂度都为 $\mathcal{O}(\log_2 n)$。

　　因为有任意删除和修改操作，涉及到第 $k$ 个插入的数，所以不能直接知道第 $k$ 个插入的数在堆中的下标是多少，所以需要写一个独特的 $\mathtt{swap}$ 操作，就有了前面所提到的两个数组 ph[N] 和 hp[N]。

　　具体看一下代码：

void heap_swap(int a, int b)
{
    swap(hp[a], hp[b]);
    swap(ph[hp[a]], ph[hp[b]]);
    swap(h[a], h[b]);
}

　　这三行的代码的意思是：先交换一下 hp 数组，再交换一下对应的 ph 数组，最后再交换堆中的元素。

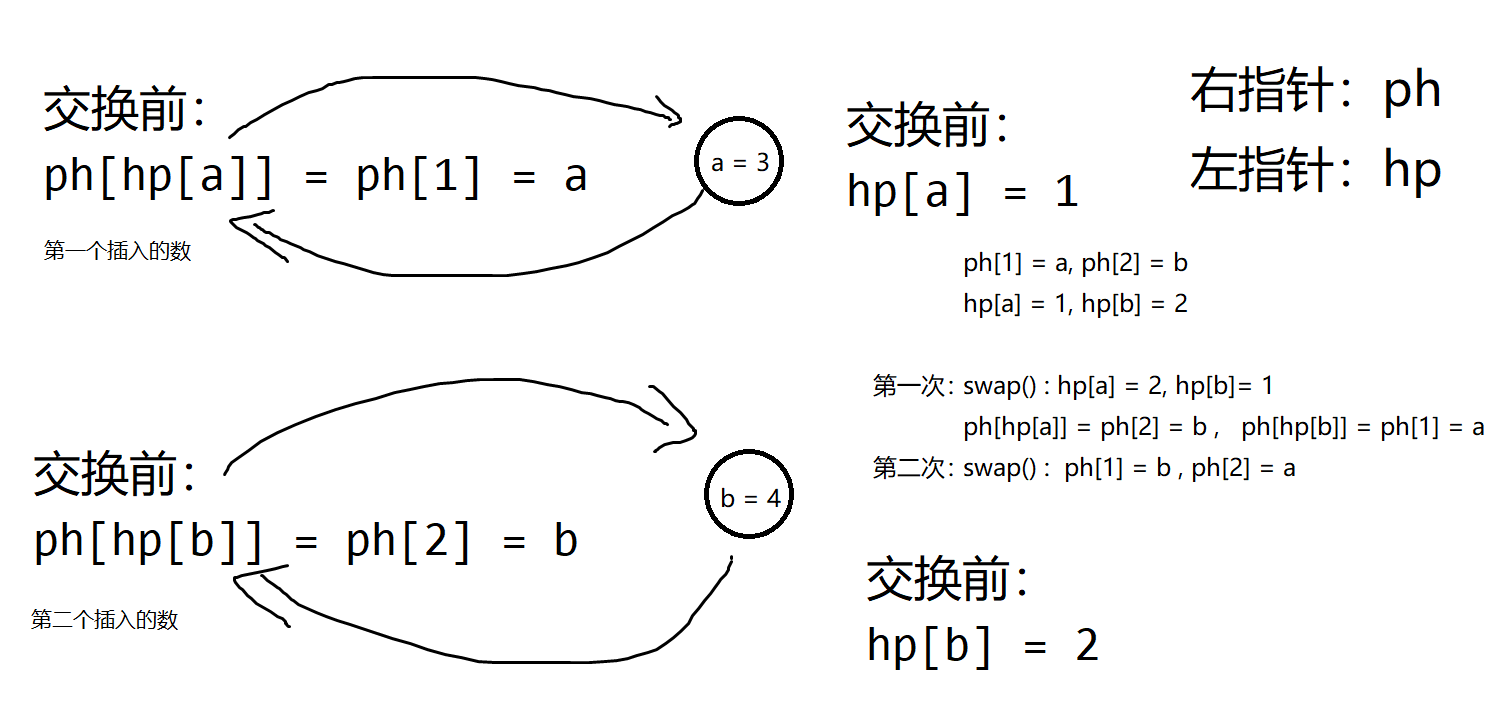
　　举个例子：第一个插入的数是 $a$，第二个插入的数是 $b$，所以：

　　 hp[a] = 1、hp[b] = 2、ph[hp[a]] = ph[1] = a、ph[hp[b]] = ph[2] = b、h[1] = 3、h[2] = 4。

　　先交换一下 hp 数组就有：hp[a] = 2，hp[b] = 1。

　　再交换一下对应的：ph 数组就有：ph[hp[a]] = ph[2] = a，ph[hp[b]] = ph[1] = b。

　　最后再交换一下对应的 h 数组：h[1] = 4，h[2] = 3。

　　具体的可以看一下图片：

图 1：交换前

图 2：交换后

　　看一下 down 操作：

void down(int u)
{
    int t = u;    // t 为：父结点、左子结点、右子结点三者的最小值
    if ((u << 1) <= cnt && h[u << 1] < h[t]) t = u << 1;
    if ((u << 1 | 1) <= cnt && h[u << 1 | 1] < h[t]) t = u << 1 | 1;
    if (u != t)    // 需要交换
    {
        heap_swap(u, t);
        down(t);
    }
}

　　 up 操作：

// up 操作，只和我的父结点进行比较
void up(int u)
{
    int t = u;
    if (u / 2 && h[u / 2] > h[t]) t = u / 2;
    if (u != t)
    {
        heap_swap(u, t);
        up(t);
    }
}

　　以上就是堆的基本操作了。