哈希表

                     

贡献者： 有机物

　　 哈希表又称散列表，哈希通常是把一些值域较大的数映射成值域较小的数。比如把 $10^8$ 映射成 $1$，$10^8 + 100$ 映射成 $2$。来看一道具体问题：

　　 维护一个集合，支持如下几种操作：

1. 插入一个数 $x$；
2. 询问数 $x$ 是否在集合中出现过；

　　 现在要进行 $N$ 次操作，对于每个询问操作输出对应的结果。

　　 数据范围：$ 1 \le N \le 10^5$，$\ -10^9 \le x \le 10^9$

　　 因为 $x$ 的值域非常大，所以我们需要设计一个哈希函数，能把一个值域比较大的数映射到从 $0 \sim 10^5$ 之间的一个数。

　　 一般哈希函数设计为 Hash(x) = (x mod P)。

　　 因为因为值域变小了，很有可能把原始值不同的两个数映射到同一个位置，所以我们需要处理这种冲突情况。处理冲突的两种方式：拉链法，开放寻址法。

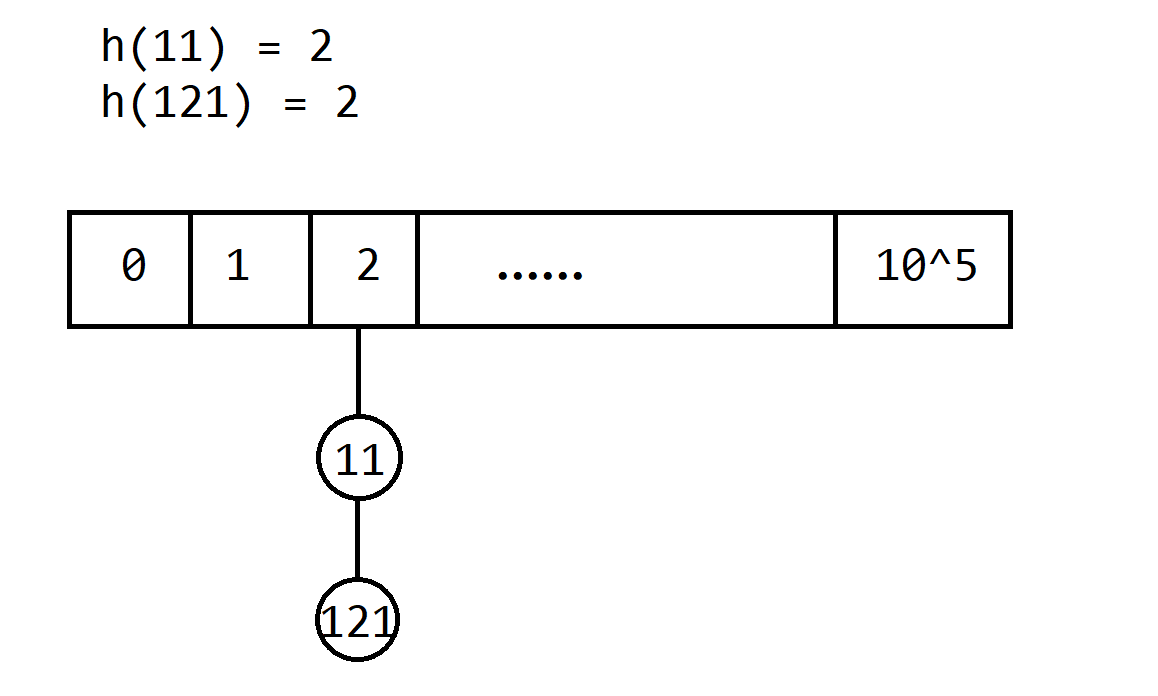
　　 拉链法：

　　 先开一个一维数组来保存每个数的哈希值，如果有数映射到了某个位置，我们就在那个位置开一个链表用于记录每个数。查询每个数是否存在的的时候，就在对应的哈希位置遍历一下整个链表，对其中的每个数比较其值与查询的值是否一致。

　　 拉链法的时间复杂度为 $O(N)$

　　 一般来说，设计哈希算法取模的数要设置为一个质数，数学上可以证明这么取冲突的概率是最小的。

const int N = 1e5 + 3;

int h[N], e[N], ne[N], idx;
int n;

// 头插法
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void insert(int x)
{
    int k = (x % N + N) % N;   // 哈希位置
    add(k, x);
}

bool find(int x)
{
    int k = (x % N + N) % N;
    for (int i = h[k]; ~i; i = ne[i])  // 遍历整个链表
        if (e[i] == x)
            return true;
    return false;
}

　　 开放寻址法：

　　 开放寻址法只需要开一个一维数组，一般数组大小要开到题目要求的 $2 \sim 3$ 倍。开放寻址法的基本思路为：如果一个位置 $k$ 不是 $x$ 的话，那么就去 $k + 1$、$k + 2$ ... 找，添加一个数为：先从第一个位置找，如果为空的话就插入 $x$。查找一个数：从第 $k$ 个位置开始找，如果当前位置为空的话说明 $x$ 不存在。

const int N = 2e5 + 10, INF = 0x3f3f3f3f;

int n, h[N];

int find(int x)
{
    int k = (x % N + N) % N;
    while (h[k] != INF && h[k] != x)    // INF = 0x3f3f3f3f
    {
        k ++ ;  // 看完了 
        if (k == N) k = 0;  // 就循环看第一个位置
    }
    
    return k;  //1、如果在哈希表内就返回 k 就是 x 的下标  2、如果不在哈希表内就返回应该存储的位置
}

memset(h, 0x3f, sizeof h);  // 表示每个数最开始都是空的

　　 以上就是处理 $\mathtt{Hash}$ 冲突的两个方式。