子集（综述）

贡献者：待更新

　　本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

图 1：欧拉图示意：A 是 B 的子集（记作 $A \subseteq B$），反之，B 是 A 的超集（记作 $B \supseteq A$）。

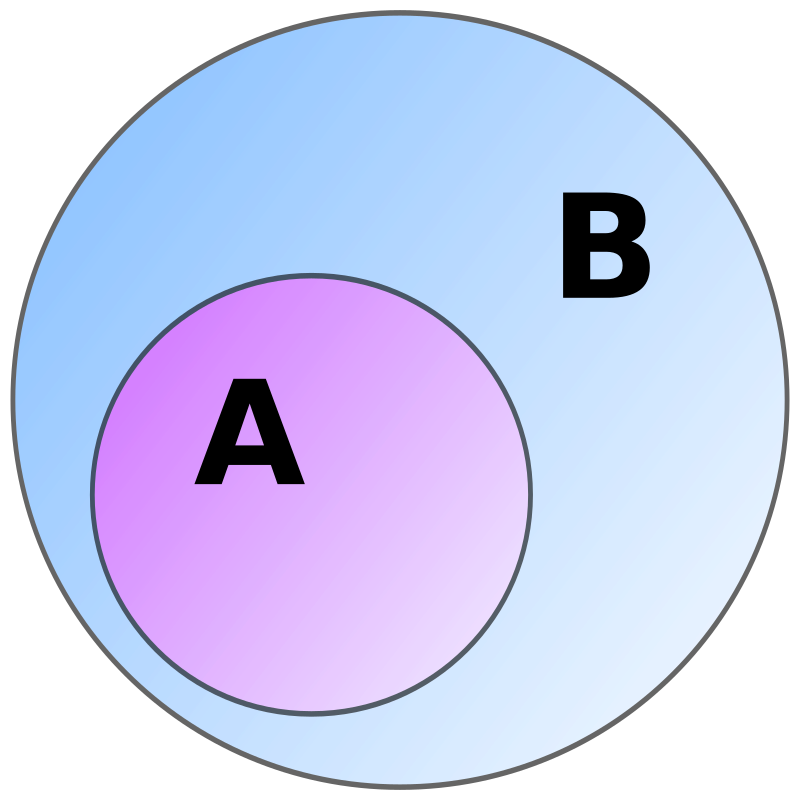
　　在数学中，如果集合 A 的所有元素也是集合 B 的元素，则称 A 是 B 的子集；此时 $B$ 是 $A$ 的超集。集合 $A$ 与 $B$ 有可能相等；如果它们不相等，则 A 是 B 的真子集。一个集合是另一个集合的子集这一关系称为包含关系（有时也称为包涵关系）。$A$ 是 $B$ 的子集也可以表述为 $B$ 包含 $A$ 或 $A$ 被包含于 $B$。一个 k-子集是指具有 k 个元素的子集。

　　在量化表示时，$A \subseteq B$ 可写作 $\forall x \,(x \in A \Rightarrow x \in B)$。

　　可以通过一种称为元素论证法的证明技巧来证明命题 $A \subseteq B$。

设给定集合 $A$ 和 $B$。要证明 $A \subseteq B$。
假设 a 是集合 A 中一个特定但任意选择的元素，并证明 a 也是集合 B 的元素。

　　这种方法的有效性可以看作是全称概化的结果：该方法表明，对于任意选择的元素 c，都有 $(c \in A) \Rightarrow (c \in B)$。由此，全称概化推出 $\forall x \,(x \in A \Rightarrow x \in B)$，这等价于 $A \subseteq B$ 如上所述。

1. 定义

　　如果 $A$ 和 $B$ 是集合，且 $A$ 的每一个元素也是 $B$ 的元素，那么：

$A$ 是 $B$ 的子集，记作 $A \subseteq B$ 或等价地，
$B$ 是 $A$ 的超集，记作 $B \supseteq A$

　　如果 A 是 B 的子集，但 A 不等于 B（即至少存在一个 B 中的元素不在 A 中），那么：

$A$ 是 $B$ 的真（或严格）子集，记作 $A \subsetneq B$ 或等价地，
$B$ 是 $A$ 的真（或严格）超集，记作 $B \supsetneq A$。

　　空集，写作 $\{\}$ 或 $\varnothing$，没有任何元素，因此平凡地是任意集合 $X$ 的子集。

2. 基本性质

图 2：$A \subseteq B \quad \text{且} \quad B \subseteq C \;\;\Rightarrow\;\; A \subseteq C$

自反性：对任意集合 $A$ 都有 $A \subseteq A$
传递性：若 $A \subseteq B$ 且 $B \subseteq C$ 则 $A \subseteq C$
反对称性：若 $A \subseteq B$ 且 $B \subseteq A$ 则 $A = B$

真子集

反自反性：对任意集合 $A$,$A \subsetneq A$ 为假。
传递性：若 $A \subsetneq B$ 且 $B \subsetneq C$,则 $A \subsetneq C$
反对称性：若 $A \subsetneq B$,则 $B \subsetneq A$ 为假。

3. 符号 ⊂ 和 ⊃

　　有些作者使用符号 $\subset$ 和 $\supset$ 分别表示子集与超集；也就是说，它们的含义与符号 $\subseteq $ 和 $\supseteq$ 相同并可以互换。例如，在这些作者看来，对于任意集合 $A$，都有 $A \subset A$，这是一个自反关系。

　　另一些作者则倾向于使用符号 $\subset$ 和 $\quad \supset$ 分别表示真子集（也称严格子集）与真超集；也就是说，它们的含义与符号 $\subsetneq $ 和 $\supsetneq$ 相同并可以互换。这种用法使得 $\subseteq$ 与 $\subset$ 类似于不等号 $\leq $ 与 $ <$ 例如，如果 $x \leq y$，那么 $x$ 可能等于 $y$，也可能不等于；但如果 $x < y$，那么 $x$ 一定不等于 $y$，而且小于 $y$（这是一个反自反关系）。同样地，在采用 “⊂ 表示真子集” 的约定下：如果 $A \subseteq B$，那么 $A$ 可能等于 $B$，也可能不等于；但如果 $A \subset B$，那么 $A$ 一定不等于 $B$。

4. 子集的例子

图 3：正多边形构成多边形的一个子集。

集合 $A = {1, 2}$ 是集合 $B = {1, 2, 3}$ 的真子集，因此表达式 $A \subseteq B(A \subseteq B)$ 和 $A \subsetneq B(A \subsetneq B)$ 都成立。
集合 $D = {1, 2, 3}$ 是集合 $E = {1, 2, 3}$ 的子集（但不是真子集），因此 $D \subseteq E(D \subseteq E)$ 成立，而 $D \subsetneq E(D \subsetneq E)$ 不成立（即为假）。
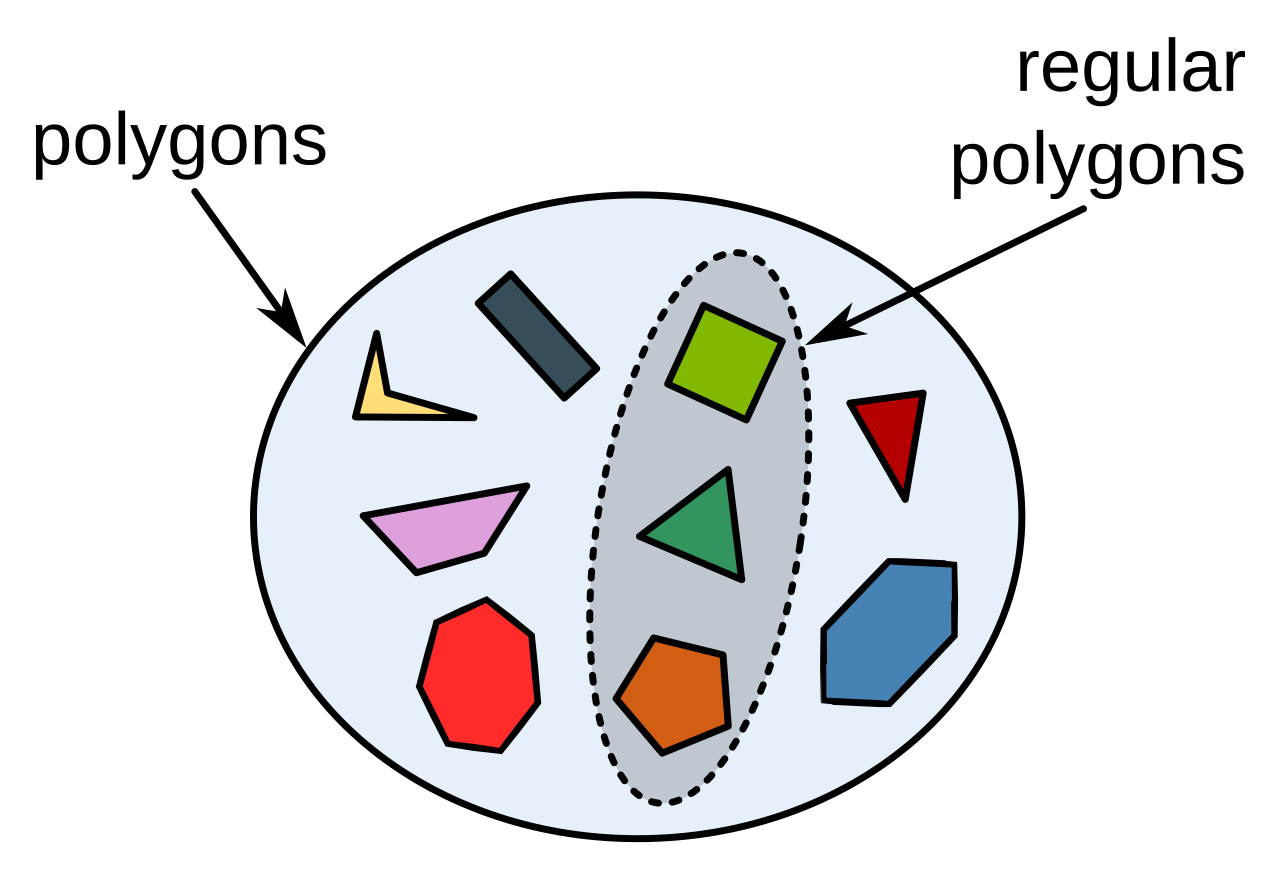
集合{x : x 是大于 10 的素数}是集合{x : x 是大于 10 的奇数}的真子集。
自然数集合是有理数集合的真子集；同样，线段上的点集是直线上点集的真子集。这是两个例子，其中子集与整体集合都是无限的，并且子集与整体集合具有相同的基数（对应于有限集的大小，即元素的数量）；这种情况可能会违背人们最初的直觉。
有理数集合是真实数集合的真子集。在这个例子中，这两个集合都是无限的，但后者集合的基数（或势）大于前者集合。

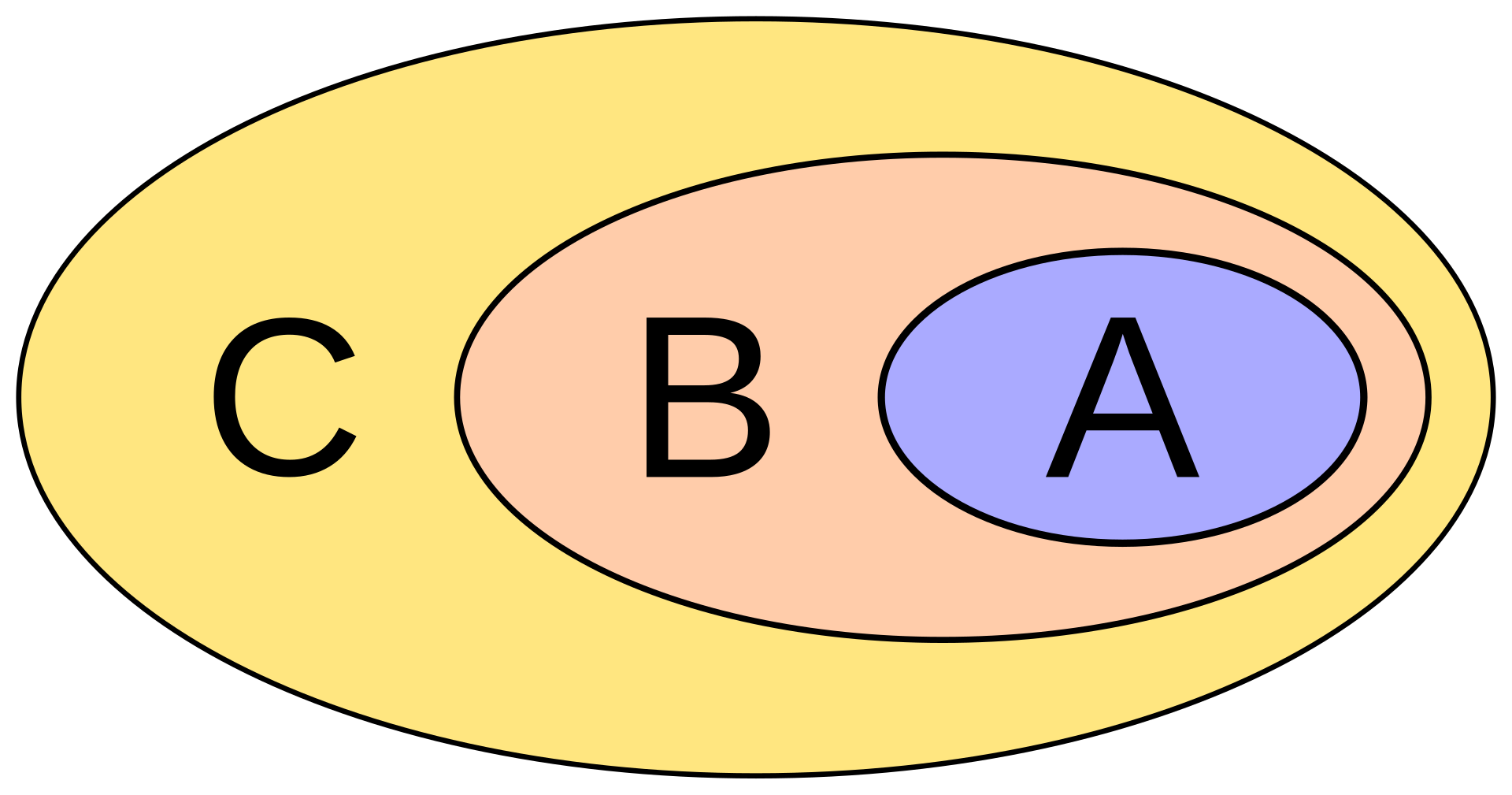
　　另一个在欧拉图中的例子：

图 4：A 是 B 的真子集。

图 5：翻译如下：C 是 B 的子集，但不是 B 的真子集。

5. 幂集

　　集合 $S$ 的所有子集所组成的集合称为它的幂集，记作 $\mathcal{P}(S)$.

　　包含关系 $\subseteq$ 在幂集 $\mathcal{P}(S)$ 上定义了一个偏序：$A \leq B \iff A \subseteq B$.

　　我们也可以用 “反向包含” 来在 $\mathcal{P}(S)$ 上定义偏序：$A \leq B $ 当且仅当 $B \subseteq A$.对于集合 $S$ 的幂集 $\mathcal{P}(S)$，其包含关系的偏序同构于 $|S|=k$ 个 $\{0,1\}$ 上偏序的笛卡尔积，其中 $\{0,1\}$ 的偏序为 $0<1$。这可以通过如下方式说明：将集合 $S = \{s_{1}, s_{2}, \ldots, s_{k}\}$ 枚举，并把每个子集 $T \subseteq S$（即 $T \in 2^{S}$）对应到一个 $\{0,1\}^{k}$ 的 k 元组：其中第 i 个坐标为 1 当且仅当 $s_i \in T$。

　　集合 $A$ 的所有 k 元子集记作 $\binom{A}{k}$,这一记号与二项式系数的记法类似，因为二项式系数表示从一个 n 元集合中选取 k 元子集的个数。在集合论中，记号 $[A]^k$ 也很常见，特别是在 $k$ 是超限基数时。

6. 包含关系的其他性质

交集刻画：集合 $A$ 是集合 $B$ 的子集，当且仅当它们的交集等于 $A$。形式化地： $$ A \subseteq B \iff A \cap B = A.~ $$
并集刻画：集合 $A$ 是集合 $B$ 的子集，当且仅当它们的并集等于 $B$。形式化地： $$ A \subseteq B \iff A \cup B = B.~ $$
有限集的基数刻画：若 $A$ 是有限集，则 $A \subseteq B$ 当且仅当 $$ |A \cap B| = |A|.~ $$
子集关系在集合上定义了一个偏序。事实上，给定集合的所有子集在子集关系下构成一个布尔代数，其中：并(join)运算是交集，交(meet)运算是并集，子集关系本身就是布尔代数中的包含关系。
包含关系是典范的偏序，意思是：任意偏序集 $(X, \preceq)$ 都同构于某个按包含关系排列的集合族。序数是一个简单的例子：如果把每个序数 $n$ 与集合 $[n] = \{ \text{所有小于等于 } n \text{ 的序数} \}$ 对应起来，则有 $a \leq b \iff [a] \subseteq [b]$.

7. 参见

凸子集 —— 在几何学中，与任意一条直线的交集都是一个线段的集合
包含序 —— 作为某类对象上的子集包含关系而产生的偏序
部分论 —— 研究 “部分” 及其所构成的 “整体” 的学科
区域 —— 拓扑空间中的连通开子集
子集和问题 —— 计算机科学中的判定问题
涵摄式包含 —— 元素彼此从属的系统
子空间 —— 具有额外结构的数学集合
全子集 —— 拓扑向量空间 $X$ 的子集 $T$，其线性生成集在 $X$ 中稠密

8. 参考文献

Rosen, Kenneth H. (2012). Discrete Mathematics and Its Applications (第 7 版). 纽约: McGraw-Hill. p.119. ISBN 978-0-07-338309-5.
Epp, Susanna S. (2011). Discrete Mathematics with Applications (第 4 版). Cengage Learning. p.337. ISBN 978-0-495-39132-6.
Stoll, Robert R. (1963). Set Theory and Logic. 旧金山, CA: Dover Publications. ISBN 978-0-486-63829-4.
Rudin, Walter (1987). Real and Complex Analysis (第 3 版). 纽约: McGraw-Hill. p.6. ISBN 978-0-07-054234-1. MR 0924157.
Subsets and Proper Subsets* (PDF), 原始版本存档于 2013-01-23, 检索于 2012-09-07.
Weisstein, Eric W. "Subset". mathworld.wolfram.com. 检索于 2020-08-23.

9. 参考书目

Jech, Thomas (2002). Set Theory. Springer-Verlag. ISBN 3-540-44085-2.

10. 外部链接

维基共享资源中与子集相关的多媒体
Weisstein, Eric W. “Subset”. MathWorld.