浙江理工大学 2011 年数据结构
贡献者: xzllxls
1. 一、单选题
在每小题的四个备选答案中选出一个正确答案,每小题 3 分,共 45 分。
1. 若线性表最常用的操作是存取第 $i$ 个元素及其前趋的值,则采用()存储方式节省时间。
A.单链表 $\qquad$ B.双链表 $\qquad$ C.单循环链表 $\qquad$ D.顺序表
2. 设输入序列为 $1$、$2$、$3$、$4$,则借助栈所得到的输出序例不可能是()
A.1、2、3、4
B.4、1、2、3
C.1、3、4、2
D.4、3、2、1
3. 常对数组进行的两种基本操作是()。
A.建立与删除
B.插入与修改
C.查找与修改
D.查找与插入
4. 数组 $Q[n]$ 用来表示个循环队列,$f$ 为当前队列头元素的前一位置, $r$ 为队尾元素的位置,假定队列中元素的个数小于 $n$ ,计算队列中元素的公式为()
A. r-f
B. (n+f-r)%n
c. n+r-f
D. (n+r-f)%n
5.广义表((a, b, C, d))的表尾是()
A. a
B.( )
C.(a,b,c, d)
D.((a,b,c,d))
6.实现任意二叉树的后序遍历的非递归算法而不使用栈结构,最佳方案是二叉树采用( )存储结构。
A.三叉链表
B.广义表存储结构
C.二叉链表
D.顺序表存储结构
7.在线索化二叉树中, $P$ 所指的结点没有左子树的充要条件是( )。
A. P->left==null
B. P->ltag=1
C. P->ltag==1 且 P->left==null
D. 以上都不对
8.稀疏矩阵一般的压缩存储方法有两种,即( )。
A.二维数组和三维数组
B.三元组和散列
C.三元组和十字链表
D.散列和十字链表
9.有 $n$ 个结点的有向图的边数最多有( )。
A. n
B. n(n-1)
C. n (n-1)/2
D. 2n
10.带权有向图 $G$ 用邻接矩阵 $A$ 存储,则顶点 $i$ 的入度等于 $A$ 中( )
A.第 $i$ 行非无穷元素之和
B.第 $i$ 列非无穷元素之和
C.第 $i$ 行非零且非无穷元素个数
D.第 $i$ 列非零且非无穷元素个数
11.采用邻接表存储的图的深度优先遍历算法类似于二叉树的()。
A.先序遍历
B.中序遍历
C.后序遍历
D.按层遍历
12.链表适用于()查找。
A.顺序
B.二分法
C.顺序,也能二分法
D.随机
13.有一个长度为 12 的有序表,按二分查找法对该表进行查找,在表内各元素等概率情况下查找成功所需的平均比较次数为
A.35/12
B.37/12
C.39/12
D.43/12
14.快速排序在下列()情况 下最易发挥其长处。
A.被排序的数据中含有多个相同排序码
B.被排序的数据已基本有序
C.被排序的数据完全无序
D.被排序的数据中的最大值和最小值相差悬殊
15.若一组记录的排序码为(46, 79, 56, 38, 40, 84),则利用堆排序的方法建立的初始堆为()。
A.79,46,56,38,40,84
B.84,79,56,38,40,46
C.84,79,56,46,40,38
D.84,56,79,40,46,38
2. 二、填空题
(每空 3 分,共 30 分。)
1.设 $n$ 为正整数,求以下程序段中以记号@的语句的频度是
k=0;
for(i=1;<=m;i++){
for(j=1;j<=n;j++)
@k++;
}
2.在一个单链表中的 $P$ 所指结点之前插入一个 $S$ 所指结点时,可执行如下操作:
S->next = P->next;
P->next = S;
T = P->data;
P->data = ( ① );
S->data = ( ② );
3.在单链表中,要删除某一指定的结点(该结点不为首元结点),必须找到该结点的( )结点。
4.在具有 $n$ 个单元的循环队列中,队满时共有( )个元素。
5.三维数组 $a[4][5][6]$(下标从 $0$ 开始计, $a$ 有 $4\times5\times6$ 个元素) ,每个元素的长度是 $2$ ,则 $a[2][3][4]$ 的地址是( )。(设 $a[0][0][0]$ 的地址是 $1000$,数据以行为主序方式存储)。
6.$5$ 层完全二叉树至少有( )个结点。
7.在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的( )倍。
8.在各种查找方法中,平均查找长度与结点个数 $n$ 无关的查找方法是( ).
9.设要将序列(Q,H,C,Y,P,A,M,S,R,D,F,X)中的关键码按字母序的升序重新排列,则冒泡排序一趟扫描的结果是( ).
3. 三、简答题
(3 题,共 45 分。)
1. (6 分)说明线性表、栈与队列的异同点。
2. (19 分)设二叉树 BTree 的存储结构如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| left | 0 | 0 | 2 | 3 | 7 | 5 | 8 | 0 | 10 | 1 |
| data | j | h | f | d | b | a | c | e | g | i |
| right | 0 | 0 | 9 | 4 | 0 | 0 | 0 | 0 | 0 | 0 |
其中,BTree 为树根结点指针, left、right 分别为结点的左、右孩子指针域,在这里使用结点编号作为指针域值, 0 表示指针域值为空; data 为结点的数据域。请完成如下问题:
(1)画出二叉树 BTree 的逻辑结构;
(2)写出按先序、中序和后序遍历二叉树 BTree 所得到的结点序列;
(3)画出二叉树 BTree 的后线索化树。
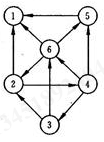
3.(20 分)已知如右图所示的有向图,请给出该图的:
(1)每个顶点的入/出度; (2)邻接矩阵; (3)邻接表; (4)逆邻接表。
4. 四、编程题
(每小题 15 分,共 30 分)
1.如果一个线性表是由循环双链表来实现的,该链表只有表头指针而没有表尾指针。请编写算法实现对该线性表进行如下运算:
(1)删除第一个元素;
(2)删除最后一个元素;
(3)在第一个元素前面插入新元素;
(4)在最后-一个元素的后面插入新元素。
注:链表中的结点定义为如下:
typedef struct node
{
elemType data;
struct node *prior;
struct node *next;
} DNode;
2.有一个不带头结点的有序单链表(从小到大排序),表头指针为 $head$,编写算法:
(1)向该单链表中插入一个元素为 $x$ 的结点,使插入后该链表仍然有序;
(2)依次输出链表中的元素。