折射(综述)
贡献者: 待更新
(本文根据 CC-BY-SA 协议转载自原搜狗科学百科对英文维基百科的翻译)
在物理学中,折射是波从一种介质传播到另一种介质传播方向的变化,或者是在介质中的传播方向逐渐变化。光的折射是最常见的折射现象,但声波和水波等其他波也会经历折射。波被折射的程度取决于波速的变化以及波传播相对于速度变化方向的初始方向。
对于光,折射遵循斯涅尔定律,该定律指出,对于给定的一对介质,入射角 $\theta_1$ 和折射角 $\theta_2$ 的正弦之比等于两种介质中的相速度之比 $(v_1 / v_2)$,或者等同于两种介质的折射率之比 $(n_2 / n_1)$。
$\frac{\sin \theta_1}{\sin \theta_2} = \frac{v_1}{v_2} = \frac{n_2}{n_1}$
光学棱镜和透镜利用折射来改变光线的方向,人眼也是如此。材料的折射率随着光的波长而变化,[3] 因此折射角也相应地变化。这被称为色散,并导致棱镜和彩虹将白光分成其组成光谱颜色。[4]
1. 常规解释
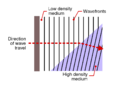
想象一个波从一种材料流向另一种传播速度较慢的材料(如图所示)。如果它以某个角度到达两种材料之间的界面,波的一侧将首先到达第二种材料,因此更早减速。随着波的一边走得越来越慢,整个波将向那一边偏折。这就是为什么当一个波进入一个较慢的物质时,它会远离表面或向法线弯曲。在相反情况(即波从一种材料流向传播速度更快的另一种材料)下,波的一侧将加速,并且波将向那一侧的方向偏折。
理解这件事情的另一种方法是考虑界面处波长的变化。当波从一种材料传播到另一种材料,其中波具有不同的速度 v,而波的频率 f 将保持不变,但是波前之间的距离或波长λ=v/f 将改变。如果速度降低,如上图的右边所示,波长也会减小。波阵面和界面之间的角度以及波阵面之间距离的变化必须在界面上改变,以保持波阵面完好无损。从以上的考虑,可以推导出两种材料中入射角θ1,、透射角θ2 和波速 v1 和 v2 之间的关系。这是折射定律或斯涅耳定律,可以写成[5]
$\frac{\sin \theta_1}{\sin \theta_2} = \frac{v_1}{v_2} $
折射现象可以从二维或三维波动方程中以更基本的方式导出。界面处的边界条件将要求界面两侧波矢的切向分量相同。[6] 由于波矢的大小取决于波速,因此波矢的方向需要改变。
上面讨论的相关波速是波的相速度。这通常接近群速度,群速度可以被视为波的真实速度,但是当它们的值不同时,在所有与折射相关的计算中使用相速度是很重要的。
垂直于界面传播的波(即其波前平行于边界),即使波的速度改变,波的传播方向也不会改变。
2. 光
光的折射在我们日常生活的许多地方都能见到。它使水面下的物体看起来比实际距离更近。它是光学透镜的基础,使得如眼镜、照相机、双筒望远镜、显微镜和人眼等仪器的实现成为可能。折射也是一些自然的光学现象的产生原因,包括彩虹和海市蜃楼。
2.1 折射定律
对于光而言,材料的折射率 $n$ 比材料中的波的相速度 $v$ 更常用。然而,它们与真空中的光速直接相关
$n = \frac{c}{v}$
因此,在光学中,折射定律通常写成
$n_1 \sin \theta_1 = n_2 \sin \theta_2$
2.2 水面折射
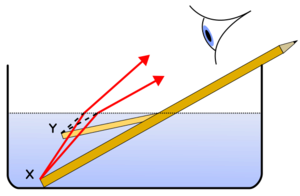
由于水的折射率为 1.33,空气的折射率约为 1,所以光线穿过水面时会发生折射。看一个笔直的物体,比如图中的铅笔,它倾斜放置,部分浸没在水中,物体看起来向水面弯曲。这是由于光从水中传播到空气中时会发生弯曲。光线一旦到达眼睛,眼睛就会以直线(视线)追踪它们。视线(如虚线所示)在比实际光线来源更高的位置相交。这使得铅笔看起来更高,水看起来比实际更浅。
从上面看时,水的深度被称为视深度。这是从水面上用鱼叉捕鱼的一个重要考虑因素,因为这将使目标鱼看起来在不同的地方,而且渔夫必须瞄准更低的地方去捕鱼。相反,当从水下观察时,水面上的物体具有更高的视高度。喷水鱼必须做相反的修正。[7]
对于小入射角(从法线测量,当 sin θ与 tan θ大致相同时),视深度与实际深度之比是空气折射率与水折射率之比。但是,当入射角接近 90°时,表观深度接近零,尽管反射率增加,这限制了大入射角时的观察。相反,视高度随着入射角(从下方)的增加而接近无穷大,但甚至更快,随着全内反射角的接近,尽管图像也随着该极限的接近而从视野中消失。
2.3 色散
折射也是彩虹现象和白光穿过玻璃棱镜时分裂成彩虹光谱的原因。玻璃的折射率比空气高。当一束白光从空气中进入折射率随频率变化的材料时,这种现象被称为光的色散,其中白光的不同颜色组分以不同的角度被折射,即它们在界面处弯曲不同的程度,从而被分离开来。不同的颜色对应着不同的频率。
2.4 大气折射
空气的折射率取决于空气密度,因此随空气温度和气压而变化。由于压力在较高的高度是较低的,空气的折射率也较低,当光线在大气中长距离传播时,会向地球的表面折射。当恒星靠近地平线时,这将稍微改变它们的视位置,并使太阳在日出时上升到地平线之前可被看见。
空气中的温度变化也会导致光线折射。当热空气和冷空气混合时,例如在火上、在发动机排气的过程中或者在寒冷的日子打开窗户时,这可以被视为热霾。这使得通过混合空气观察的物体看起来像是随着冷热空气的移动而闪烁或随机移动。当使用高放大倍数的远摄镜头时,这种效果在晴天气温的正常变化中也是可见的,并且在这些情况下经常影响图像质量。[8] 同样地,大气湍流在天文望远镜的图像中产生快速变化的畸变,使得不使用自适应光学或其他技术无法克服这些大气畸变的地面望远镜的分辨率。
靠近地表的气温变化会引起其他光学现象,如海市蜃楼。最常见的情况是,在阳光明媚的日子里,被炎热的道路加热的空气会使光线以一个较浅的角度转向观察者。这使得道路看起来是反光的,给人一种有水覆盖道路的错觉。
3. 水波
水波在浅水中传播较慢。这可以用来证明水波槽中的折射,也解释了为什么海岸线上的水波倾向于以接近垂直的角度撞击海岸。当水波从深水行进到靠近海岸的浅水中时,它们从最初的行进方向折射到更垂直于海岸线的角度。[9]
4. 临床意义
在医学领域,尤其是在验光、眼科和整形外科中,屈光检查(也称为折射计)是一种临床试验,在这种试验中,合适的眼科专业人员可以使用综合屈光检查仪来确定眼睛的屈光误差和需要配置的最佳矫正镜片。从一系列分级光学倍率或焦距的测试透镜中确定哪一个提供最清晰的视觉。[10]
5. 声学
在水下声学中,折射是指声线从一个声速区域到另一个不同声速区域通过声速梯度时产生的弯曲或弯曲。声线弯曲的程度取决于声速之间的差异,即水温、盐度和水压的变化。[11]在地球大气层中也发现了类似的声学效应。声音在大气中折射的现象在几个世纪前已经被发现了;[12] 然而,从 20 世纪 70 年代初开始,通过设计城市高速公路和隔音屏障来解决低层大气中声波弯曲的气象效应,人们对这种效应的广泛分析开始流行。[13]
6. 隧道效应
7. 参考文献
- The Editors of Encyclopaedia Britannica. "Refraction". Encyclopaedia Britannica. Retrieved 2018-10-16..
- Born and Wolf (1959). Principles of Optics. New York, NY: Pergamon Press INC. p. 37..
- R. Paschotta, article on chromatic dispersion Archived 2015-06-29 at the Wayback Machine in the Encyclopedia of Laser Physics and Technology Archived 2015-08-13 at the Wayback Machine, accessed on 2014-09-08.
- Carl R. Nave, page on Dispersion Archived 2014-09-24 at the Wayback Machine in HyperPhysics Archived 2007-10-28 at the Wayback Machine, Department of Physics and Astronomy, Georgia State University, accessed on 2014-09-08.
- Hecht, Eugene (2002). Optics. Addison-Wesley. p. 101. ISBN 0-321-18878-0..
- "Refraction". RP Photonics Encyclopedia. RP Photonics Consulting GmbH, Dr. Rüdiger Paschotta. Retrieved 2018-10-23. It results from the boundary conditions which the incoming and the transmitted wave need to fulfill at the boundary between the two media. Essentially, the tangential components of the wave vectors need to be identical, as otherwise the phase difference between the waves at the boundary would be position-dependent, and the wavefronts could not be continuous. As the magnitude of the wave vector depends on the refractive index of the medium, the said condition can in general only be fulfilled with different propagation directions..
- Dill, Lawrence M. (1977). "Refraction and the spitting behavior of the archerfish (Toxotes chatareus)". Behavioral Ecology and Sociobiology. 2 (2): 169–184. doi:10.1007/BF00361900. JSTOR 4599128..
- "The effect of heat haze on image quality". Nikon. 2016-07-10. Retrieved 2018-11-04..
- "Shoaling, Refraction, and Diffraction of Waves". University of Delaware Center for Applied Coastal Research. Archived from the original on 2009-04-14. Retrieved 2009-07-23..
- "Refraction". eyeglossary.net. Archived from the original on 2006-05-26. Retrieved 2006-05-23..
- Navy Supplement to the DOD Dictionary of Military and Associated Terms (PDF). Department Of The Navy. August 2006. NTRP 1-02.[永久失效连结].
- Mary Somerville (1840), On the Connexion of the Physical Sciences, J. Murray Publishers, (originally by Harvard University).
- Hogan, C. Michael (1973). "Analysis of highway noise". Water, Air, & Soil Pollution. 2 (3): 387–392. Bibcode:1973WASP....2..387H. doi:10.1007/BF00159677..