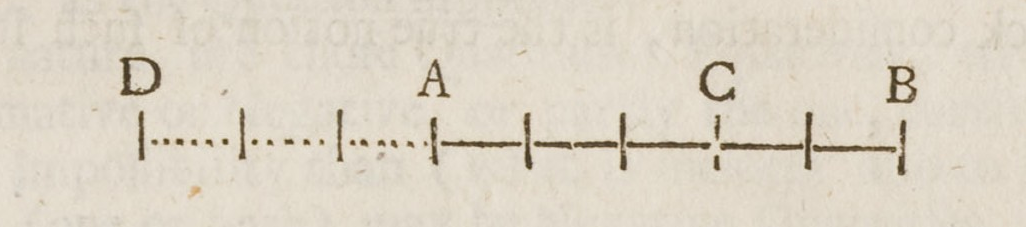约翰·沃利斯（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1：约翰·沃利斯

　　 约翰·沃利斯（/ˈwɒlɪs/；[2]拉丁语：Wallisius；1616 年 12 月 3 日 [旧历 11 月 23 日] – 1703 年 11 月 8 日 [旧历 10 月 28 日]）是英国的一位牧师和数学家，部分功劳归于他对微积分发展的贡献。

　　 1643 年至 1689 年间，沃利斯担任议会及后来王室的首席密码学家。[3] 他被认为引入了符号 ∞ 来表示无穷的概念。[4] 他同样使用 1/∞ 表示无穷小。他是牛顿的同时代人，也是数学早期复兴时期最伟大的知识分子之一。[5]

1. 传记

教育背景

家庭

　　 1645 年 3 月 14 日，他与苏珊娜·格莱德（约 1600 年 – 1687 年 3 月 16 日）结婚。他们有三个孩子：

2. 生活

　　 约翰·沃利斯出生于肯特郡的阿什福德。他是约翰·沃利斯牧师和乔安娜·查普曼的五个孩子中的第三个。起初他在阿什福德的一所学校接受教育，但由于瘟疫爆发，他于 1625 年转入滕特登的詹姆斯·莫瓦特学校。1631 年，沃利斯在费尔斯特学校（当时称为费尔斯特的马丁·霍尔比奇学校）首次接触数学；他对数学很感兴趣，但学习却不太系统，因为 “在当时，数学在我们这儿几乎不被视为学术研究，而是机械学科”（Scriba 1970）。在费尔斯特学校，沃利斯学会了说和写拉丁语。到那时，他还熟练掌握了法语、希腊语和希伯来语。[9] 由于家人希望他成为一名医生，他于 1632 年被送到剑桥大学伊曼纽尔学院。[10] 在那里，他进行了一次关于血液循环理论的辩论，据说这是欧洲首次在辩论中公开维护这一理论。然而，他的兴趣集中在数学上。1637 年，他获得了文学学士学位，1640 年获得硕士学位，随后进入牧师行列。1643 年至 1649 年间，他担任威斯敏斯特大会的无表决权书记。1644 年，他当选为剑桥大学皇后学院的研究员，但在结婚后不得不辞去这一职位。

　　 在此期间，沃利斯一直与议会党关系密切，这可能是由于他在费尔斯特学校受到了霍尔比奇的影响。他在破解保皇党密电方面为他们提供了极大的实际帮助。那时的密码学质量参差不齐；尽管像弗朗索瓦·维埃特这样的数学家取得了个别成功，但加密设计和分析的基本原理仍然很少被理解。大多数密码是基于秘密算法的临时方法，而非基于可变密钥的系统。沃利斯意识到后者要安全得多，甚至将其描述为 “不可破解”，尽管他对这一论断的信心不足，以至于不敢鼓励公开密码算法。此外，他还担心外国势力使用密码，例如，1697 年，他拒绝了戈特弗里德·莱布尼茨关于教授汉诺威学生密码学的请求。[11]

　　 回到伦敦后——1643 年他成为了圣加布里埃尔芬丘奇的牧师——沃利斯加入了一个科学家小组，这个小组后来演变为皇家学会。他终于能够满足自己对数学的兴趣，1647 年在几周内掌握了威廉·奥特雷德的《数学钥匙》。他很快开始撰写自己的论文，涉及广泛的主题，并持续了他的一生。沃利斯撰写了关于英国数学概念的第一份综述，其中讨论了印地-阿拉伯数字系统。[12]

　　 沃利斯加入了温和派的长老会，签署了反对处决查理一世的抗议书，因此遭到了独立派的长期敌视。尽管他们反对，1649 年他仍被任命为牛津大学萨维尔几何学教授，并一直居住在牛津，直至 1703 年 11 月 8 日（旧历 10 月 28 日）去世。1650 年，沃利斯被授予牧师身份。之后，他作为私人牧师与理查德·达利爵士和维尔夫人共度了两年。1661 年，他作为十二位长老会代表之一参加了萨沃伊会议。[citation needed]

　　 除了他的数学著作外，他还撰写了神学、逻辑、英语语法和哲学方面的作品，并参与设计了一种在利特尔科特庄园教授聋哑男孩说话的方法。[13] 威廉·霍尔德早些时候曾教授一名聋人亚历山大·波普汉姆说话，使其 “发音清晰、优雅且语调得当”。[14] 后来，沃利斯声称对此功劳归于自己，导致霍尔德指责他 “掠夺邻人，以他人之成果装饰自己”。[15]

沃利斯被任命为牛津大学萨维尔几何学教授

　　 议会对牛津的访问始于 1647 年，这次访问免去了许多高级学者的职务，包括 1648 年 11 月被免职的萨维尔几何学和天文学教授。1649 年，沃利斯被任命为萨维尔几何学教授。沃利斯的选择似乎主要基于政治原因（他的保皇派前任彼得·特纳也可能是如此，尽管他被任命为两个教授职位，却从未发表任何数学作品）；虽然沃利斯或许是当时全国领先的密码学家，且是后来成为皇家学会的非正式科学家小组的成员，但他并没有作为数学家的特别名声。尽管如此，沃利斯的任命在他随后担任萨维尔教授的 54 年里，通过他的工作得到了充分的证明。[16]

3. 对数学的贡献

图
图 2：《数学作品集》，1699

　　 沃利斯在三角学、微积分、几何学和无穷级数分析方面作出了重要贡献。在他的《数学作品集 I》（1695 年）中，他引入了 “连分数” 一词。

解析几何

　　 1655 年，沃利斯发表了一篇关于圆锥曲线的论文，在其中对这些曲线进行了解析定义。这是第一本将这些曲线视为并定义为二次曲线的书籍，有助于消除人们对笛卡尔解析几何工作中某些难以理解的内容的困惑。

　　 在《圆锥曲线论》中，沃利斯普及了用于表示无穷的符号 \(\infty\)。他写道：“我假设任何平面（遵循卡瓦列里的不可分量几何学）是由无数条平行线组成的，或者更确切地说，是由无数个相同高度的平行四边形组成的；（令这些平行四边形的每一个高度为整个高度的一个无穷小部分 \(1/\infty\)，并让符号 \(\infty\) 表示无穷），而所有这些高度的和构成图形的总高度。”[17]

积分学

　　 《无穷算术》是沃利斯最重要的著作之一，出版于 1656 年。在这篇论文中，笛卡尔和卡瓦列里的分析方法得到了系统化和扩展，但其中的一些观点仍有争议。他在简短地论述了圆锥曲线后，开始发展幂的标准表示法，并将其从正整数扩展到有理数： \[ x^0 = 1~ \] \[ x^{-1} = \frac{1}{x}~ \] \[ x^{-n} = \frac{1}{x^n} \text{ 等等}~ \] \[ x^{1/2} = \sqrt{x}~ \] \[ x^{2/3} = \sqrt[3]{x^2} \text{ 等等}~ \] \[ x^{1/n} = \sqrt[n]{x}~ \] \[ x^{p/q} = \sqrt[q]{x^p}~ \] 这些扩展统一了指数表示法，为数学分析提供了基础。

　　 略去这一发现的众多代数应用，沃利斯接着通过积分求得了曲线 \(y = x^m\)、x 轴和任意纵坐标 \(x = h\) 所围成的面积，并证明了该面积与在相同基底和相同高度上的平行四边形的面积之比为 \(1 / (m + 1)\)，从而扩展了卡瓦列里的求积公式。他显然假定对于曲线 \(y = ax^m\) 也同样成立，其中 \(a\) 是任意常数，\(m\) 是任何正或负的数，但他仅讨论了抛物线（\(m = 2\)）和双曲线（\(m = -1\)）的情况。在后者的情况下，他对结果的解释是错误的。

　　 他接着展示了对于任意形式为 \[ y = \sum a x^m~ \] 的曲线，可以写出类似的结果，因此，如果曲线的纵坐标 \(y\) 可以展开为 \(x\) 的幂次，其面积就可以确定：因此他指出，如果曲线的方程是 \(y = x^0 + x^1 + x^2 + \dots\)，则其面积将为 \(x + x^2/2 + x^3/3 + \dots\)。他随后将此应用于曲线 \(y = (x - x^2)^0\)、\(y = (x - x^2)^1\)、\(y = (x - x^2)^2\) 等，在区间 \(x = 0\) 到 \(x = 1\) 之间的求积。他展示了这些面积分别为 1, \(1/6\), \(1/30\), \(1/140\) 等。

　　 接着，他考虑了形式为 \(y = x^{1/m}\) 的曲线，并建立了一个定理：由该曲线与直线 \(x = 0\) 和 \(x = 1\) 所围成的面积等于在相同基底和高度上的矩形的面积之比，即 \(m : (m + 1)\)。这相当于计算 \[ \int_{0}^{1} x^{1/m} \, dx~ \] 他以抛物线 \(m = 2\) 为例进行了说明。他指出了形式为 \(y = x^{p/q}\) 的曲线的相应结果，但未加以证明。

　　 沃利斯在将曲线方程简化为上述形式时展现了相当的巧思，但由于他不熟悉二项式定理，无法对圆进行求积。圆的方程为 \(y = \sqrt{1 - x^2}\) 因为他无法将其展开成 \(x\) 的幂次形式。不过，他提出了插值的原理。因此，由于圆的纵坐标 \(y = \sqrt{1 - x^2}\) 是曲线 \(y = (1 - x^2)^0v\) 和 \(y = (1 - x^2)^1\) 的纵坐标的几何平均数，可以假设，作为一种近似，半圆的面积 \(\int_{0}^{1} \sqrt{1 - x^2} \, dx\) 即 \(\frac{1}{4} \pi\) 可以被视为以下两个值的几何平均： \[ \int_{0}^{1} (1 - x^2)^0 \, dx \quad \text{和} \quad \int_{0}^{1} (1 - x^2)^1 \, dx~\]

　　 即 1 和 \(\frac{2}{3}\)；这相当于将 \(\pi\) 的值取为 \(4 \sqrt{\frac{2}{3}} \approx 3.26...\)。但是，沃利斯提出，实际上我们有一个序列 \(1, \frac{1}{6}, \frac{1}{30}, \frac{1}{140}, \dots\) 因此，插入在 1 和 \(\frac{1}{6}\) 之间的项应符合该序列的规律。[需要进一步说明] 通过一种复杂的方法（此处未详细描述），得到了插值项的值，相当于取 \[ \frac{\pi}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdots~ \] （这现在被称为 “沃利斯积”）。

　　 在这项工作中，他还讨论了连分数的形成和性质，这一主题因布朗克使用连分数而受到关注。

　　 几年后，即 1659 年，沃利斯发表了一篇小论文，包含了解决布莱兹·帕斯卡提出的摆线问题的方案。在其中，他附带解释了如何利用他在《无穷算术》中提出的原理来求解代数曲线的长度问题，并给出了对半三次抛物线 \(x^3 = ay^2\) 的求解（即确定其长度），这条曲线于 1657 年由他的学生威廉·尼尔发现。由于所有试图确定椭圆和双曲线长度的尝试都（必然地）无效，因此一直认为没有曲线的长度可以被求出，笛卡尔甚至明确地断言了这一点。对数螺线的长度已被埃万杰利斯塔·托里切利确定，是第一个（除圆之外）长度已知的曲线，但尼尔和沃利斯将这一结果扩展到代数曲线，这是一个新颖的进展。接下来被确定长度的曲线是摆线，这项工作由克里斯托弗·雷恩于 1658 年完成。[citation needed]

　　 1658 年初，赫拉特也独立于尼尔发现了类似的结果，并由范·斯库滕在 1659 年笛卡尔《几何学》的版本中出版。赫拉特的方法如下：他假设曲线参照矩形坐标轴；如果是这样，且 \((x, y)\) 是曲线上任意一点的坐标，\(n\) 是法线的长度，[需要进一步说明] 如果另一点的坐标为 \((x, \eta)\)，并且满足 \(\eta : h = n : y\)，其中 \(h\) 是一个常数，那么，如果 \(ds\) 是所求曲线的长度元素，根据相似三角形有 \(ds : dx = n : y\)。因此，\(h \, ds = \eta \, dx\)。因此，如果可以找到点 \((x, \eta)\) 所在轨迹的面积，则可以求出第一条曲线的长度。通过这种方式，赫拉特成功地求出了曲线 \(y^3 = ax^2\) 的长度，但他补充说，抛物线 \(y^2 = ax\) 的长度无法求出，因为它需要双曲线的求积。尼尔和沃利斯给出的解法与赫拉特的方法有些相似，尽管他们没有提出通用规则，且分析较为笨拙。第三种方法由费马于 1660 年提出，但其方法不优雅且繁琐。

物体碰撞

　　 1668 年，皇家学会提出了物体碰撞理论，供数学家们研究。沃利斯、克里斯托弗·雷恩和克里斯蒂安·惠更斯提供了正确且相似的解答，所有解答都依赖于现在称为动量守恒的概念。然而，雷恩和惠更斯将他们的理论仅限于完全弹性物体（弹性碰撞），而沃利斯则考虑了不完全弹性物体（非弹性碰撞）。随后在 1669 年，他撰写了一部关于静力学（重心）的著作，并在 1670 年撰写了一部关于动力学的著作，这些著作为当时该领域的知识提供了便捷的概述。

代数学

　　 1685 年，沃利斯出版了《代数学》，其中包含了代数学发展历程的历史概述，提供了大量有价值的信息。1693 年出版的第二版，作为他《作品集》的第二卷，进行了相当大的扩充。这本代数学著作的显著特点是包含了公式的首次系统性使用。在这里，一个给定的量被表示为它与同类单位之间的数值比率：例如，当沃利斯想要比较两个长度时，他将每个长度视为包含若干个单位长度。通过观察沃利斯如何表示一个粒子在任意时间内以恒定速度运动时所描述的空间关系，或许可以更清楚地理解这一点，他用公式表示为 \[ s = vt,~ \] 其中 \(s\) 表示所描述的空间与长度单位的比率；而以前的作者会通过陈述等同于以下命题的内容来表示相同的关系： \[ s_1 : s_2 = v_1 t_1 : v_2 t_2~ \]

数轴

图
图 3：在《代数学论》中，沃利斯提到从点 \(A\) 前进和后退时写道：“…\(-3\) 确实表示点 \(D\)；就如同 \(+3\) 表示点 \(C\)…并且每个（至少在同一条无限直线上）都表示一个唯一的点：而且只有一个。”

　　 沃利斯被认为是 “为负量” 和 “为操作目的” 引入数轴的发起人[18][19]。这一观点基于他 1685 年《代数学论》中的一段话，他在其中引入了数轴以说明负量的合理性：[20]

　　 “这种（负量的）假设在正确理解的情况下既不无用也不荒谬。尽管就纯粹的代数符号来说，它表示小于零的量；但在物理应用中，它表示的量与符号为 \(+\) 时一样真实，只是要以相反的意义来解释……\(+3\) 表示向前 3 码，而 \(-3\) 表示向后 3 码。”

　　 有人指出，在更早的著作中，沃利斯得出结论，正数与负数之比大于无穷大。这个论证涉及到商 \(\frac{1}{x}\) 并考虑当 \(x\) 接近并越过点 \(x = 0\)（从正数侧接近）时会发生什么情况。[21] 沃利斯并不是唯一持有这一观点的人：莱昂哈德·欧拉也通过考虑几何级数 \(\frac{1}{1 - x} = 1 + x + x^2 + \cdots\) 在 \(x = 2\) 的情况，并结合类似于沃利斯的推理得出相同结论（他通过区分不同类型的负数来解决这个悖论）。[18]

几何学

　　 他通常被认为是使用相似三角形证明勾股定理的人。然而，阿拉伯数学家萨比特·伊本·库拉（公元 901 年）早在六个世纪前就已经提出了适用于所有三角形的勾股定理的推广版本。据推测，沃利斯可能知晓萨比特的工作。[22]

　　 沃利斯还受到伊斯兰数学家萨德尔·图西（纳西尔·丁·图西之子）作品的启发，特别是图西 1298 年关于平行公设的书。该书基于他父亲的思想，并提出了最早的一个等价于平行公设的非欧几里得假设。阅读该书后，沃利斯开始撰写自己的想法，试图通过相似三角形来证明该公设。[23]

　　 他发现欧几里得第五公设等价于现在以他命名的 “沃利斯公设”。该公设指出：“在给定的一条有限直线上，总是可以构造一个与给定三角形相似的三角形”。这一结果属于从其他四个公设中推导出欧几里得第五公设的尝试，今天已知这是不可能的。与其他作者不同的是，他认识到前三个公设并不能保证三角形的无限扩展。[24]

计算能力

　　 沃利斯数学才能的另一个方面是他进行心算的能力。他睡眠不好，常常在躺在床上清醒时做心算。某晚，他在脑海中计算了一个 53 位数的平方根。第二天早晨，他完全凭记忆口述出该数的 27 位平方根。这一成就被认为非常惊人，皇家学会秘书亨利·奥尔登堡特地派同事调查沃利斯是如何做到的。这一成就被认为十分重要，以至于在 1685 年的《皇家学会哲学会刊》中进行了讨论。[25][26]

4. 音乐理论

　　 沃利斯将托勒密和布莱尼乌斯的作品以及波菲利对托勒密的评论翻译成拉丁文。他还发表了三封给亨利·奥尔登堡的信，讨论了音律。他赞同当时在英国管风琴中使用的平均律。[27]

5. 其他作品

图
图 4：《数学作品集》，1657 年

　　 他于 1687 年出版的《逻辑学教程》非常受欢迎。[4]《英语语法》是一部关于英语语法的著作，一直在 18 世纪广泛印行。他还发表了有关神学的著作。[4]

6. 沃利斯作为密码学家

　　 1642 年，沃利斯在担任维尔夫人的牧师时，收到了一封关于奇切斯特陷落的加密信件，他在两小时内成功解密了这封信，从此开启了他的密码学家生涯。在第一次英国内战中，他适度支持议会党，因此为议会领袖们解读截获的信件。作为报酬，他获得了伦敦圣加布里埃尔教堂和圣马丁教堂的教职。[28]

　　 由于他支持议会党，在斯图亚特王朝复辟后，沃利斯没有被聘为密码学家。[29] 但在光荣革命后，诺丁汉勋爵找到他，频繁地雇佣他解读截获的加密信件，尽管沃利斯认为自己并不总是获得了应得的报酬。[a] 从 1689 年起，威廉三世国王也聘请沃利斯担任密码学家，有时几乎是每日一聘。信使们会把需要解密的信件带到他家，并在他书房外等待解密结果。1689 年，威廉三世曾写信给荷兰大议长安东尼·海因休斯，表现出对沃利斯工作及其健康的关切。[29]

　　 在威廉三世统治初期，直接获得外国截获的信件对英国来说是一个难题，因为当时他们还没有外国 “黑室” 的资源。不过，像勃兰登堡选帝侯这样没有自己的 “黑室” 的盟友，偶尔会赠送此类截获的信件，例如 1689 年，威廉三世利用法国国王路易十四致波兰国王约翰三世·索别斯基的信件，引发了法波外交危机。他对此相当坦诚，沃利斯因此得到了嘉奖。[31] 然而，沃利斯开始担心法国可能会对他采取行动。[32]

　　 沃利斯与德国数学家戈特弗里德·威廉·莱布尼茨的关系融洽。但莱布尼茨对密码学也感兴趣，并试图让沃利斯透露一些他的行业机密，然而沃利斯出于爱国原则，拒绝了他的请求。[33]

　　 史密斯给出了沃利斯工作的一个例子，这是沃利斯在 1689 年 8 月 3 日写给理查德·汉普顿的一封信中描述的。在信中，他详细描述了自己对某封信件的工作以及遇到的部分困难。[34]

　　 沃利斯的通信还显示了他如何为自己辩护的细节，尤其是在他觉得自己在财务或其他方面未被充分重视时。他积极游说，既为自己，也为他的亲属谋取利益，这在他写给诺丁汉勋爵、理查德·汉普顿和议员哈博德·哈博德的信件中有所体现，正如史密斯引用的那样。[35] 在给英国驻普鲁士特使詹姆斯·约翰斯顿的信中，沃利斯愤愤不平地抱怨普鲁士选帝侯的一位名叫斯梅特奥的侍臣在支付公正报酬方面亏待了他。信中，他详细描述了自己所做的工作，并向约翰斯顿提出了一种简单的替换密码供其使用。[36]

　　 沃利斯对密码学的贡献不仅具有 “技术性” 特征。德·李乌指出，沃利斯在语言学领域的 “理性” 自然语言发展方面的 “纯科学” 贡献，也对密码学作为一门科学的发展起到了作用。沃利斯提出的独立于早期拉丁语语法模型的英语语法模型，正是他认为其他科学帮助发展密码学的一个典型案例。[37]

　　 沃利斯试图将密码学的技巧传授给自己的儿子约翰，以及女儿安妮的孙子威廉·布伦克夫。对于威廉，他取得了很大的成功，以至于他说服政府允许孙子继承他因密码学工作而获得的每年 100 英镑的养老金。[38]

　　 在沃利斯 1703 年去世后，威廉·布伦克夫最终接替他成为安妮女王的官方密码学家。[39]

7. 另见

8. 注释

　　 a.史密斯引用了他有时带有尖刻语气的给诺丁汉等人的信件。[30]

9. 参考文献

  1. Joseph Frederick Scott, 《约翰·沃利斯的数学工作 (1616-1703)》，泰勒与弗朗西斯，1938 年，第 109 页。
  2. 《兰登豪斯词典》。
  3. David Eugene Smith (1917). “约翰·沃利斯作为密码学家”。《美国数学学会公报》. 24 (2): 82–96. doi:10.1090/s0002-9904-1917-03015-7. MR 1560009.
  4. Hugh Chisholm, 编. (1911). “沃利斯, 约翰”。《大英百科全书》。第 28 卷（第 11 版）。剑桥大学出版社，第 284–285 页。
  5. D. A. Kearns (1958). “约翰·沃利斯与复数”。《数学教师》. 51 (5): 373–374. JSTOR 27955680.
  6. Joan Thirsk (2005). “布伦科夫夫人安妮 (1656–1718)”。《牛津国家人物传记词典》。牛津国家人物传记词典（在线版）。牛津大学出版社。doi:10.1093/ref:odnb/41326. 取自 2023 年 8 月 21 日。（需订阅或英国公共图书馆会员）。
  7. “沃利斯, 约翰 (1650-1717), Soundness, Nettlebed, Oxon。”《英国议会历史在线》。取自 2023 年 8 月 21 日。
  8. “伊丽莎白·沃利斯”。《早期现代书信在线：人物》。取自 2023 年 8 月 21 日。
  9. Yule, G. Udny (1939)。“约翰·沃利斯，神学博士，皇家学会会员”。《伦敦皇家学会的记录与注释》。2 (1): 74–82. doi:10.1098/rsnr.1939.0012. JSTOR 3087253。
  10. “Wallys, John (WLS632J)”。《剑桥校友数据库》。剑桥大学。
  11. Kahn, David (1967)，《破译者：秘密书写的故事》，纽约：麦克米伦出版社，第 169 页，LCCN 63016109。
  12. 4
  13. “发现可能结束 350 年的科学争议”。BBC。2008 年 7 月 26 日。取自 2018 年 5 月 5 日。
  14. Holder, W. (1668)。“关于一项关于失聪的实验”。《皇家学会哲学会刊》3，第 665-668 页。
  15. Holder，《皇家学会哲学会刊》，增刊，第 10 期。
  16. “约翰·沃利斯：时间线”，maths.ox.ac.uk。访问日期：2024 年 4 月 19 日。
  17. Scott, J.F. (1981)。《约翰·沃利斯的数学工作，神学博士，皇家学会会员（1616–1703）》。切尔西出版公司，纽约，第 18 页。
  18. Heeffer, Albrecht (2011 年 3 月 10 日)。“对数轴的历史性反对意见”。《科学与教育》。20 (9): 863–880 [872–876]。Bibcode:2011Sc&Ed..20..863H. doi:10.1007/s11191-011-9349-0. hdl:1854/LU-1891046. S2CID 120058064。
  19. Núñez, Rafael (2017)。“有多少数学是‘硬连线’的，如果有的话：生物进化、发展和文化的基本作用” (PDF)。收录于 Sera, Maria D.; Carlson, Stephanie M.; Maratsos, Michael (编辑)，《明尼苏达儿童心理学研讨会：文化与发展系统》第 38 卷。约翰·威立公司，第 83–124 页 [96]。doi:10.1002/9781119301981.ch3。
  20. Wallis, John (1685)。《代数学论，历史与实践》。伦敦：理查德·戴维斯出版社，第 265 页。MPIWG:GK8U243K。
  21. Martínez, Alberto A. (2006)。《负数学：如何正向扭转数学规则》。普林斯顿大学出版社，第 22 页。ISBN 978-0-691-12309-7。取自 2013 年 6 月 9 日。
  22. Joseph, G.G. (2000)。《孔雀的冠冕：数学的非欧洲根源》（第二版）。企鹅出版社，第 337 页。ISBN 978-0-14-027778-4。
  23. Katz, Victor J.，《埃及、两河流域、中国、印度和伊斯兰的数学：资料集》，普林斯顿大学出版社，存档于 2016 年 10 月 1 日于 Wayback Machine。
  24. Burton, David M. (2011)，《数学史/导论》（第 7 版），麦格劳-希尔公司，第 566 页，ISBN 978-0-07-338315-6。
  25. Dr. Wallis (1685) “《牛津哲学学会期刊的两段摘录；其中一篇包含了该学会主席沃利斯博士在 1685 年 3 月 31 日发表的关于在适当注意力应用下记忆力的强度的论文……》”，《伦敦皇家学会哲学会刊》，15：1269-1271。在线版本：伦敦皇家学会 [永久失效链接]。
  26. Hoppen, K. Theodore (2013)，《17 世纪的普通科学家：都柏林哲学学会研究，1683–1708》，Routledge 图书馆版：科学史与哲学，第 15 卷，Routledge，第 157 页，ISBN 9781135028541。
  27. David Damschoder 和 David Russell Williams，《从扎尔利诺到申克的音乐理论：书目与指南》（纽约斯蒂文桑特：潘德拉贡出版社，1990），第 374 页。
  28. Smith，第 83 页
  29. De Leeuw (1999)，第 138 页
  30. Smith，第 83-86 页
  31. Smith，第 87 页
  32. De Leeuw (1999)，第 139 页
  33. Smith，第 83-84 页
  34. Smith，第 85-87 页
  35. Smith，第 89-93 页
  36. Smith，第 94-96 页
  37. De Leeuw (2000)，第 9 页
  38. Cave, E.，编. (1788)。“沃利斯博士的原始信件及其养老金的一些细节”，《绅士杂志》，63 (1788 年 6 月): 479–480。取自 2023 年 8 月 20 日。
  39. De Leeuw (1999)，第 143 页

10. 资料来源

　　 本文的初始文本来自公共领域资源：

11. 外部链接

                     

© 小时科技 保留一切权利