薛定谔方程（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 薛定谔方程是一个偏微分方程，用于描述非相对论量子力学体系的波函数的演化过程。\(^\text{[1]: 1–2 }\) 它的发现是量子力学发展史上的一个重要里程碑。该方程以奥地利物理学家埃尔温·薛定谔的名字命名。他于 1925 年提出该方程，并于 1926 年发表，从而奠定了其后获得 1933 年诺贝尔物理学奖的工作基础。\(^\text{[2][3]}\)

　　 在概念上，薛定谔方程是量子力学中对应于经典力学中牛顿第二定律的表达。给定一组已知的初始条件，牛顿第二定律可以用数学方式预测一个物理系统随时间演化的轨迹。薛定谔方程则给出了波函数随时间的演化规律，而波函数是对一个孤立物理系统的量子力学描述。该方程是薛定谔在路易·德布罗意提出 “所有物质都具有伴随的物质波” 这一假设的基础上提出的。薛定谔方程成功预测了与实验观测一致的原子束缚态。\(^\text{[4]: II:268 }\)

　　 薛定谔方程并不是研究量子力学系统和进行预测的唯一方法。量子力学的其他表述方式还包括维尔纳·海森堡提出的矩阵力学，以及主要由理查德·费曼发展的路径积分表述。在比较这些方法时，使用薛定谔方程的方式有时被称为 “波动力学”。

　　 薛定谔提出的方程是非相对论性的，因为它在时间上是一阶导数，而在空间上是二阶导数，因此空间与时间在方程中并不对等。保罗·狄拉克将狭义相对论与量子力学结合成一个统一的表述形式，在非相对论极限下会简化为薛定谔方程。这就是狄拉克方程，它在空间和时间上都只包含一阶导数。

　　 另一个偏微分方程，即克莱因–戈尔登方程，虽然是一个相对论性的波动方程，但在描述概率密度时出现了问题：概率密度可能为负值，这在物理上是不可接受的。狄拉克通过对克莱因–戈尔登算符进行所谓的 “开平方” 处理，引入了狄拉克矩阵，从而解决了这一问题。

　　 在现代物理的语境中，克莱因–戈尔登方程用于描述无自旋粒子，而狄拉克方程则用于描述自旋为 1/2 的粒子。

1. 定义

预备知识

　　 在物理或化学的入门课程中，通常会以一种仅需掌握基础微积分（特别是关于空间与时间的导数）的概念和符号就能理解的方式来介绍薛定谔方程。薛定谔方程的一个特例，是针对一维空间中单个非相对论粒子的位置空间形式，其表达如下： $$ i\hbar \frac{\partial}{\partial t}\Psi(x,t) = \left[ -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial x^2} + V(x,t) \right] \Psi(x,t)~ $$ 在这个方程中，$\Psi(x, t)$ 是波函数，即为每个时刻 $t$ 下的每个位置 $x$ 分配一个复数值的函数；$m$ 是粒子的质量；$V(x, t)$ 是势能函数，用来表示粒子所处环境中的势场 \(^\text{[5]: 74 }\)；$i$ 是虚数单位；$\hbar$ 是约化普朗克常数，其单位为作用量（能量乘以时间）\(^\text{[5]: 10 }\)。

　　 在超越上述简单情形的更广义框架中，保罗·狄拉克 \(^\text{[6]}\)、大卫·希尔伯特 \(^\text{[7]}\)、约翰·冯·诺依曼 \(^\text{[8]}\) 和赫尔曼·外尔 \(^\text{[9]}\) 等人所发展出的量子力学数学表述，规定一个量子力学系统的状态是一个向量 $|\psi\rangle$，它属于一个可分的复希尔伯特空间 $\mathcal{H}$。该向量被假定在希尔伯特空间的内积下是归一化的，即用狄拉克记号表示，它满足 $\langle \psi | \psi \rangle = 1$ 这个希尔伯特空间的具体形式取决于所研究的系统。例如：用于描述位置和动量的希尔伯特空间是平方可积函数空间 $L^2$；用于描述单个质子的自旋的希尔伯特空间则是二维复向量空间 $\mathbb{C}^2$，配有通常的内积形式 \(^\text{[5]: 322 }\)。

　　 感兴趣的物理量 —— 例如位置、动量、能量、自旋 —— 由可观测量来表示，而可观测量是作用于希尔伯特空间上的自伴算符。一个波函数可以是某个可观测量的本征矢，这种情况下称其为该可观测量的本征态，与之对应的本征值表示该本征态下该物理量所取的值。更一般地，一个量子态通常是多个本征态的线性叠加，这被称为量子叠加态。当对某个可观测量进行测量时，结果将是该算符的某个本征值，其出现的概率由玻恩规则给出：在最简单的情形中，如果本征值 $\lambda$ 是非简并的（即仅对应一个本征态），那么概率由 $|\langle \lambda | \psi \rangle |^2$ 给出，其中 $|\lambda\rangle$ 是与本征值 $\lambda$ 对应的本征矢。更一般的情形中，如果本征值是简并的（即对应多个本征态），那么概率由 $\langle \psi | P_{\lambda} | \psi \rangle$ 给出，其中 $P_{\lambda}$ 是投影到对应本征子空间（本征空间）上的投影算符。\(^\text{[note 1]}\)

　　 例如，一个动量本征态将是一个无限延伸的完全单色波，它不是平方可积函数；同样，一个位置本征态将是一个狄拉克δ分布，它也不是平方可积函数，甚至严格来说并不属于函数范畴。因此，它们都不属于粒子的希尔伯特空间。物理学家有时将这些超出希尔伯特空间的本征态视为 “广义本征矢”。这类状态用于计算上的便利，但不表示实际的物理态 \(^\text{[10][11]: 100–105}\) 。因此，如上文中所使用的位置空间波函数 $\Psi(x, t)$ 可以写成时间相关态矢 $|\Psi(t)\rangle$ 与非物理但便于计算的 “位置本征态” $|x\rangle$ 的内积形式： $$ \Psi(x, t) = \langle x | \Psi(t) \rangle~ $$

含时薛定谔方程

　　 薛定谔方程的形式取决于具体的物理情境。其中最一般的形式是含时薛定谔方程，它描述了一个随时间演化的系统 \(^\text{[12]: 143}\) ：

　　 含时薛定谔方程（一般形式） $$ i\hbar \frac{d}{dt}|\Psi(t)\rangle = \hat{H}|\Psi(t)\rangle~ $$ 其中，$t$ 是时间，$|\Psi(t)\rangle$ 是量子系统的态矢（$\Psi$ 为希腊字母 psi），$\hat{H}$ 是一个可观测量，称为哈密顿算符。

　　 “薛定谔方程” 一词既可以指这一一般形式，也可以特指其非相对论版本。这个一般形式的方程非常通用，广泛应用于整个量子力学领域，包括狄拉克方程和量子场论等情形，通过代入不同形式的哈密顿量来适配不同系统。而特定的非相对论版本是一种近似形式，在许多实际情况下能给出精确的结果，但其适用范围有限（参见相对论量子力学和相对论量子场论）。

　　 在应用薛定谔方程时，首先需写出系统的哈密顿量，即考虑构成该系统的粒子的动能与势能，然后将其代入薛定谔方程中。由此得到的偏微分方程通过求解波函数来获得，而波函数包含了关于该系统的全部信息。在实际操作中，通常取波函数的绝对值的平方作为概率密度函数来使用 \(^\text{[5]: 78 }\)。例如，对于一个在位置空间中的波函数 $\Psi(x, t)$，我们有： $$ \Pr(x, t) = |\Psi(x, t)|^2~ $$

定态薛定谔方程

　　 前述的含时薛定谔方程预测波函数可以形成驻波，称为定态。这些态具有特别重要的意义，因为研究它们可以简化对任意初始态的含时薛定谔方程的求解过程。定态还可以通过一个更简洁的形式来描述，即定态薛定谔方程（含时项被省略的版本）。

　　 定态薛定谔方程（一般形式） $$ \hat{H}|\Psi\rangle = E|\Psi\rangle~ $$ 其中，$E$ 是系统的能量 \(^\text{[5]: 134  }\)。该形式仅在哈密顿量本身不显含时间的情况下使用。然而，即使在这种情况下，整个波函数仍然依赖于时间，这一点将在后文关于线性叠加的部分中进一步解释。从线性代数的角度来看，这就是一个本征值方程，因此波函数是哈密顿算符的本征函数，其对应的本征值为 $E$。

2. 性质

线性性

　　 薛定谔方程是一个线性微分方程，这意味着如果两个态矢量 $|\psi_1\rangle$ 和 $|\psi_2\rangle$ 是薛定谔方程的解，那么任意线性组合 $$ |\psi\rangle = a|\psi_1\rangle + b|\psi_2\rangle~ $$ 也是它的解，其中 $a$ 和 $b$ 是任意复数 \(^\text{[13]: 25   }\)。此外，这种求和还可以扩展为任意多个态矢量的线性组合。

　　 这一性质允许量子态的叠加态仍然是薛定谔方程的解。更一般地说，一个薛定谔方程的通解可以通过对一组基态进行加权求和得到。常见的一种选择是使用能量本征态作为基底，这些本征态是定态薛定谔方程的解。在这种基底下，一个含时的态矢量 $|\Psi(t)\rangle$ 可以表示为以下线性组合： $$ |\Psi(t)\rangle = \sum_n A_n e^{-iE_n t/\hbar} |\psi_{E_n}\rangle~ $$ 其中，$A_n$ 是复数系数，$|\psi_{E_n}\rangle$ 是定态薛定谔方程的解，满足： $$ \hat{H}|\psi_{E_n}\rangle = E_n |\psi_{E_n}\rangle~ $$

幺正性

　　 在哈密顿算符 $\hat{H}$ 为常量的情况下，薛定谔方程的解为 \(^\text{[12]}\)： $$ |\Psi(t)\rangle = e^{-i\hat{H}t/\hbar} |\Psi(0)\rangle~ $$ 其中， $$ \hat{U}(t) = e^{-i\hat{H}t/\hbar}~ $$ 被称为时间演化算符，它是一个幺正算符，即它保持希尔伯特空间中任意两个向量之间的内积不变【13】。幺正性是薛定谔方程所描述的时间演化的一个基本特性。

　　 如果初始态为 $|\Psi(0)\rangle$，那么任意时刻 $t$ 的态将由幺正算符 $\hat{U}(t)$ 给出： $$ |\Psi(t)\rangle = \hat{U}(t) |\Psi(0)\rangle~ $$ 反过来，假设 $\hat{U}(t)$ 是一族由参数 $t$ 标定的连续幺正算符，我们可以在不失一般性的前提下选取参数化方式，使得：$\hat{U}(0)$ 是单位算符；对任意 $N > 0$，都有 $\hat{U}(t/N)^N = \hat{U}(t)$。

　　 那么，$\hat{U}(t)$ 必然满足如下形式： $$ \hat{U}(t) = e^{-i\hat{G}t}~ $$ 其中 $\hat{G}$ 是某个自伴算符，称为这族幺正算符的生成元。哈密顿量正是这种生成元之一（在自然单位制中，$\hbar$ 被设为 1，因此该因子可忽略）。

　　 为了验证生成元是厄米的，可以考虑： $$ \hat{U}(\delta t) \approx \hat{U}(0) - i\hat{G} \delta t~ $$ 那么有： $$ \hat{U}(\delta t)^\dagger \hat{U}(\delta t) \approx (\hat{U}(0)^\dagger + i\hat{G}^\dagger \delta t)(\hat{U}(0) - i\hat{G} \delta t) = I + i\delta t(\hat{G}^\dagger - \hat{G}) + O(\delta t^2)~ $$ 因此，只有当 $\hat{G}^\dagger = \hat{G}$ 时，即 $\hat{G}$ 是厄米算符，$\hat{U}(t)$ 才能保持幺正性（至少在一阶近似下）\(^\text{[15]}\)。

基变换

　　 薛定谔方程通常是以位置的函数形式来呈现的，但从矢量-算符的角度看，它在希尔伯特空间中任何一个完备的 ket 基底下都可以有有效的表述。如前所述，为了计算的方便，也可以使用超出物理希尔伯特空间之外的 “基底”。这一点可以通过对非相对论、无自旋粒子的位置空间与动量空间薛定谔方程的比较来说明 \(^\text{[11]: 182}\) 。对于这类粒子，其希尔伯特空间是三维欧几里得空间上的复数平方可积函数空间，其哈密顿算符由一个关于动量算符的二次动能项和一个势能项组成： $$ i\hbar \frac{d}{dt}|\Psi(t)\rangle = \left( \frac{1}{2m} \hat{p}^2 + \hat{V} \right) |\Psi(t)\rangle~ $$ 记 $\mathbf{r}$ 为三维位置矢量，$\mathbf{p}$ 为三维动量矢量，则位置空间中的薛定谔方程为： $$ i\hbar \frac{\partial}{\partial t} \Psi(\mathbf{r}, t) = -\frac{\hbar^2}{2m} \nabla^2 \Psi(\mathbf{r}, t) + V(\mathbf{r}) \Psi(\mathbf{r}, t)~ $$ 而其动量空间对应形式涉及波函数和势能的傅里叶变换： $$ i\hbar \frac{\partial}{\partial t} \tilde{\Psi}(\mathbf{p}, t) = \frac{\mathbf{p}^2}{2m} \tilde{\Psi}(\mathbf{p}, t) + (2\pi\hbar)^{-3/2} \int d^3\mathbf{p}' \, \tilde{V}(\mathbf{p} - \mathbf{p}') \tilde{\Psi}(\mathbf{p}', t)~ $$ 其中， $\Psi(\mathbf{r}, t)$ 和 $\tilde{\Psi}(\mathbf{p}, t)$ 是由态矢量 $|\Psi(t)\rangle$ 派生出来的： $$ \Psi(\mathbf{r}, t) = \langle \mathbf{r} | \Psi(t) \rangle~ $$ $$ \tilde{\Psi}(\mathbf{p}, t) = \langle \mathbf{p} | \Psi(t) \rangle~ $$ 注意，这里的 $|\mathbf{r}\rangle$ 和 $|\mathbf{p}\rangle$ 并不属于希尔伯特空间本身，但它们与希尔伯特空间中所有元素之间的内积都是良定义的。

　　 当将三维空间限制为一维时，位置空间中的薛定谔方程就简化为前文所给出的薛定谔方程的第一种形式。量子力学中位置与动量之间的关系在一维情况下尤为直观。在规范量子化中，经典变量 $x$ 和 $p$ 被提升为自伴算符 $\hat{x}$ 和 $\hat{p}$，它们满足如下的基本对易关系： $$ [\hat{x}, \hat{p}] = i\hbar~ $$ 这意味着 \(^\text{[11]: 190 }\)： $$ \langle x | \hat{p} | \Psi \rangle = -i\hbar \frac{d}{dx} \Psi(x)~ $$ 也就是说，在位置表象中，动量算符 $\hat{p}$ 的作用是：$\hat{p} = -i\hbar \frac{d}{dx}$ 从而，$\hat{p}^2$ 对应的是二阶导数；而在三维中，这个二阶导数就变成了拉普拉斯算符 $\nabla^2$。

　　 基本对易关系还意味着：位置算符与动量算符是傅里叶共轭的。因此，原本在位置变量下定义的函数可以通过傅里叶变换转换为动量变量下的函数 \(^\text{[5]: 103–104 }\)。在固体物理中，薛定谔方程常用动量表述形式写出，因为布洛赫定理保证了周期性晶格势能只会将 $\tilde{\Psi}(p)$ 与 $\tilde{\Psi}(p + \hbar K)$ 耦合在一起，这里 $K$ 是离散的倒格矢。这使得在布里渊区中的每个点上，可以相互独立地求解动量空间中的薛定谔方程 \(^\text{[16]: 138}\) 。

概率流密度

　　 薛定谔方程与局域概率守恒是一致的 \(^\text{[11]: 238 }\)。它还确保一个归一化的波函数在时间演化后仍然保持归一化。在矩阵力学中，这意味着时间演化算符是一个幺正算符 \(^\text{[17]}\) 。相比之下，例如克莱因–戈尔登方程，尽管可以通过重新定义波函数的内积使其对时间不变，但波函数模平方的总体体积积分却不一定是时间不变的 \(^\text{[18]}\) 。

　　 在非相对论量子力学中，概率的连续性方程表示为： $$ \frac{\partial}{\partial t} \rho(\mathbf{r}, t) + \nabla \cdot \mathbf{j} = 0~ $$ 其中： $$ \mathbf{j} = \frac{1}{2m} \left( \Psi^* \hat{\mathbf{p}} \Psi - \Psi \hat{\mathbf{p}} \Psi^* \right) = -\frac{i\hbar}{2m} \left( \psi^* \nabla \psi - \psi \nabla \psi^* \right) = \frac{\hbar}{m} \operatorname{Im}(\psi^* \nabla \psi)~ $$ 这里的 $\mathbf{j}$ 被称为概率流密度或概率通量（即单位面积上的概率流量）。

　　 如果将波函数表示为： $$ \psi(\mathbf{x}, t) = \sqrt{\rho(\mathbf{x}, t)} \exp\left( \frac{i S(\mathbf{x}, t)}{\hbar} \right)~ $$ 其中 $S(\mathbf{x}, t)$ 是实函数，表示波函数的复相位，那么概率流密度可以写为： $$ \mathbf{j} = \frac{\rho \nabla S}{m}~ $$ 因此，波函数相位的空间变化被认为描述了波函数的概率流。尽管 $\frac{\nabla S}{m}$ 表面上类似于 “速度”，但它并不代表粒子在某一点的速度，因为位置与速度的同时测量违背了不确定性原理 \(^\text{[17]}\) 。

变量分离法

　　 如果哈密顿量不显含时间，薛定谔方程可以写成如下形式： $$ i\hbar \frac{\partial}{\partial t} \Psi(\mathbf{r}, t) = \left[-\frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r})\right] \Psi(\mathbf{r}, t)~ $$ 左边的算符只与时间有关，右边的算符只与空间有关。用变量分离法求解这个方程的思路是：设解为一个空间部分与时间部分的乘积形式 \(^\text{[19]}\)： $$ \Psi(\mathbf{r}, t) = \psi(\mathbf{r}) \, \tau(t)~ $$ 其中，$\psi(\mathbf{r})$ 是仅依赖于粒子空间坐标的函数，$\tau(t)$ 是仅依赖于时间的函数。将该形式代入薛定谔方程左侧可以发现，时间部分 $\tau(t)$ 只是一个相位因子： $$ \Psi(\mathbf{r}, t) = \psi(\mathbf{r}) \, e^{-iEt/\hbar}~ $$ 这类解被称为定态解，因为其随时间变化的部分是纯相位因子，在通过玻恩规则计算概率密度时会被抵消，不影响可观测量 \(^\text{[[12]: 143ff ]}\)。

　　 波函数的空间部分满足如下的时间无关方程 \(^\text{[20]}\)： $$ \nabla^2 \psi(\mathbf{r}) + \frac{2m}{\hbar^2} [E - V(\mathbf{r})] \psi(\mathbf{r}) = 0~ $$ 其中能量 $E$ 也出现在之前时间部分的相位因子中。

　　 这个形式可以推广到任意粒子数和任意维度的系统（只要势能不含时间）：时间无关薛定谔方程的驻波解对应的是具有确定能量的状态，而不是能量叠加的概率分布。在物理学中，这些驻波称为 “定态” 或 “能量本征态”；在化学中，它们被称为 “原子轨道” 或 “分子轨道”。能量本征态构成一个基底：任意波函数都可以表示为对离散能量态的和、或对连续能量态的积分，更一般地说，是对某个测度的积分。这体现了谱定理：在有限维的状态空间中，这对应于厄米矩阵本征矢的完备性。

　　 变量分离法对于时间无关薛定谔方程同样非常有用。例如，根据问题的对称性，可以在笛卡尔坐标系下将变量分离，如： $$ \psi(\mathbf{r}) = \psi_x(x) \psi_y(y) \psi_z(z)~ $$ 或者在球坐标系下将变量分离为径向与角向部分： $$ \psi(\mathbf{r}) = \psi_r(r) \psi_\theta(\theta) \psi_\phi(\phi)~ $$

3. 示例

无限势阱中的粒子

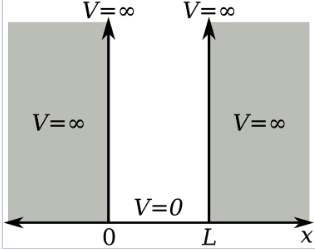
　　 一维势阱中的粒子是最简单的数学模型之一，它展示了如何通过边界条件约束导致能级量子化。这个 “势阱” 被定义为：在某一固定区域内势能为零，而在区域外势能为无限大.\(^\text{[11]: 77–78 }\)。对于 $x$ 方向上的一维情况，定态薛定谔方程可以写为： $$ -\frac{\hbar^2}{2m} \frac{d^2\psi}{dx^2} = E\psi~ $$ 如果定义微分算符为： $$ \hat{p}_x = -i\hbar \frac{d}{dx}~ $$ 那么上面的方程就与经典动能公式具有类似形式： $$ \frac{1}{2m} \hat{p}_x^2 = E~ $$ 此时，波函数 $\psi$ 的能量 $E$ 恰好对应于粒子的**动能**。 在 “盒中粒子” 模型下，薛定谔方程的一般解为： $$ \psi(x) = A e^{ikx} + B e^{-ikx}, \quad \quad E = \frac{\hbar^2 k^2}{2m}~ $$ 也可以使用欧拉公式将其表示为三角函数形式： $$ \psi(x) = C \sin\left(kx\right) + D \cos\left(kx\right) ~ $$ 势阱的无限高势能墙决定了 $C$、$D$ 和 $k$ 的取值，具体地说，要求波函数 $\psi$ 在 $x = 0$ 和 $x = L$ 处为零。因此，在 $x = 0$ 处： $$ \psi(0) = 0 = C \sin\left(0\right) + D \cos\left(0\right) = D~ $$ 由此得出：$D = 0$ 接着在 $x = L$ 处： $$ \psi(L) = 0 = C \sin\left(kL\right) ~ $$ 由于 $C$ 不能为零（否则波函数 $\psi$ 将为零函数，不符合归一化条件 $\|\psi\| = 1$），因此必须满足：$ \sin\left(kL\right) = 0$ 这意味着 $kL$ 必须是 $\pi$ 的整数倍： $$ k = \frac{n\pi}{L}, \quad n = 1, 2, 3, \dots~ $$ 这一对 $k$ 的限制，进一步对能量 $E$ 的取值也提出了限制，得出如下量子化的能级： $$ E_n = \frac{\hbar^2 \pi^2 n^2}{2mL^2} = \frac{n^2 h^2}{8mL^2}~ $$ 有限势阱是无限势阱模型的推广，其势阱深度是有限的。相比于无限势阱，有限势阱的数学处理更为复杂，因为在势阱边界处，波函数不再被强制为零，而是需要满足更复杂的边界条件——波函数在阱外区域为非零。另一个相关的问题是矩形势垒，它构成了量子隧穿效应的基本模型。该效应在现代技术中扮演着重要角色，例如闪存和扫描隧道显微镜的工作原理就依赖于此。

简谐振子

　　 在这种情况下，薛定谔方程为： $$ E\psi = -\frac{\hbar^2}{2m} \frac{d^2\psi}{dx^2} + \frac{1}{2} m \omega^2 x^2 \psi~ $$ 其中 $x$ 是位移，$\omega$ 是角频率。该方程不仅描述了量子简谐振子的行为，还可用作其他多种系统的近似模型，例如：原子、分子的振动 \(^\text{[21]}\)，晶格中原子或离子的运动 \(^\text{[22]}\)，以及在平衡点附近对其他势能函数进行近似。它也是量子力学中微扰法的基础模型之一。

　　 在位置空间中的解为： $$ \psi_n(x) = \sqrt{\frac{1}{2^n n!}} \left( \frac{m\omega}{\pi \hbar} \right)^{1/4} e^{- \frac{m\omega x^2}{2\hbar}} \, \mathcal{H}_n \left( \sqrt{\frac{m\omega}{\hbar}} x \right)~ $$ 其中 $n \in \{0, 1, 2, \ldots\}$，$\mathcal{H}_n$ 是阶数为 $n$ 的 Hermite 多项式。

　　 这一组解还可以由以下生成形式给出： $$ \psi_n(x) = \frac{1}{\sqrt{n!}} \left( \sqrt{ \frac{m\omega}{2\hbar} } \right)^n \left( x - \frac{\hbar}{m\omega} \frac{d}{dx} \right)^n \left( \frac{m\omega}{\pi\hbar} \right)^{\frac{1}{4}} e^{- \frac{m\omega x^2}{2\hbar}}~ $$ 其本征值为： $$ E_n = \left(n + \frac{1}{2} \right) \hbar \omega~ $$ 当 $n = 0$ 时的解称为基态，其能量称为零点能，对应的波函数是一个高斯函数 \(^\text{[23]}\)。

　　 与 “盒中粒子” 类似，简谐振子模型体现了薛定谔方程的一个通性：束缚态的能量本征值是离散的 \(^\text{[11]: 352 }\)。

氢原子

　　 氢原子（或类似氢原子的系统）中电子的薛定谔方程为： $$ E \psi = -\frac{\hbar^2}{2\mu} \nabla^2 \psi - \frac{q^2}{4\pi \varepsilon_0 r} \psi~ $$ 其中：$q$ 是电子的电荷，$\mathbf{r}$ 是电子相对于原子核的位置向量，$r = |\mathbf{r}|$ 是该相对位置的模，势能项来自于库仑相互作用，$\varepsilon_0$ 是真空介电常数， $$ \mu = \frac{m_q m_p}{m_q + m_p}~ $$ 是电子质量 $m_q$ 和质子质量 $m_p$ 所构成的两体系统的约化质量。势能项前的负号是因为质子与电子的电荷符号相反（一个为正，一个为负）。之所以使用约化质量而不是单独使用电子质量，是因为在这个系统中，电子和质子实际上是绕着它们的质心相互运动的，因此本质上是一个两体问题。为简化计算，可等效为电子以约化质量 $\mu$ 绕固定质子运动，即转化为一个等效的一体问题。

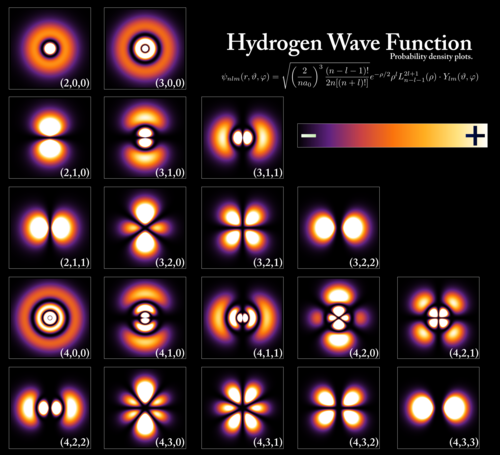
　　 氢原子的薛定谔方程可以通过变量分离法来求解 \(^\text{[24]}\)。在这种情况下，使用球坐标系最为方便。因此，波函数写作： $$ \psi(r, \theta, \varphi) = R(r) Y_{\ell}^{m}(\theta, \varphi) = R(r)\, \Theta(\theta)\, \Phi(\varphi)~ $$ 其中，$R(r)$ 是径向函数，$Y_{\ell}^{m}(\theta, \varphi)$ 是球谐函数，其中 $\ell$ 为角量子数，$m$ 为磁量子数。这是唯一一个可以精确求解薛定谔方程的原子。对于多电子原子，必须采用近似方法。氢原子的一般解为 \(^\text{[25]}\)： $$ \psi_{n\ell m}(r,\theta,\varphi) = \sqrt{\left( \frac{2}{n a_0} \right)^3 \frac{(n - \ell - 1)!}{2n[(n + \ell)!]}} \cdot e^{-r / (n a_0)} \cdot \left( \frac{2r}{n a_0} \right)^\ell \cdot L_{n - \ell - 1}^{2\ell + 1} \left( \frac{2r}{n a_0} \right) \cdot Y_\ell^m(\theta, \varphi)~ $$ 其中：

• $a_0 = \dfrac{4\pi \varepsilon_0 \hbar^2}{m_q q^2}$ 是玻尔半径；
• $L_{n - \ell - 1}^{2\ell + 1}(\cdots)$ 是广义拉盖尔多项式，次数为 $n - \ell - 1$；
• $n$、$\ell$、$m$ 分别是主量子数、角量子数和磁量子数，其取值范围为：$n = 1, 2, 3, \dots$ $\ell = 0, 1, 2, \dots, n - 1$ $m = -\ell, \dots, \ell$

近似解

　　 在大多数具有实际物理意义的情形中，薛定谔方程通常无法精确求解。因此，通常采用一些方法来获得近似解，例如变分法和 WKB 近似。此外，也常见的做法是将所研究的问题视为某个可精确求解问题的微小修正，这种方法称为微扰理论。

4. 半经典极限

　　 比较经典力学与量子力学的一种简单方法，是考察期望位置与期望动量随时间的演化，并将其与经典力学中普通的位置和动量随时间的演化进行比较 \(^\text{[26]: 302 }\)。

　　 在量子力学中，期望值满足艾伦费斯特定理（Ehrenfest 定理）。对于一个在势能 $V$ 中运动的一维量子粒子，该定理表述如下： $$ m \frac{d}{dt} \langle x \rangle = \langle p \rangle \quad \frac{d}{dt} \langle p \rangle = -\langle V'(X) \rangle~ $$ 其中，第一个方程与经典行为一致，而第二个方程则不完全一致：如果 $(\langle X \rangle, \langle P \rangle)$ 要满足牛顿第二定律，那么第二个方程右边应当是： $$ - V'\left( \langle X \rangle \right)~ $$ 但这通常并不等于：$- \langle V'(X) \rangle$ 因此，对于一般形式的势函数导数 $V'$，量子力学的预测中，期望值并不一定会模拟经典行为。

　　 然而，在量子简谐振子的情形下，$V'$ 是线性的，这种差异就会消失。因此在这种特殊情况下，期望位置与期望动量确实会完全遵循经典轨迹。对于一般系统，我们所能期望的最理想情况是：期望位置和期望动量大致遵循经典轨迹。如果波函数高度集中于某个位置点 $x_0$ 附近，那么： $$ V'\left( \langle X \rangle \right) \approx \langle V'(X) \rangle \approx V'(x_0)~ $$ 在这种情况下，期望位置与动量就会非常接近经典轨迹——至少在波函数在空间中仍高度局域化的时间范围内，会保持这种近似。

　　 薛定谔方程的一般形式： $$ i\hbar \frac{\partial}{\partial t} \Psi(\mathbf{r}, t) = \hat{H} \Psi(\mathbf{r}, t)~ $$ 与哈密顿-雅可比方程（HJE）密切相关： $$ - \frac{\partial}{\partial t} S(q_i, t) = H\left(q_i, \frac{\partial S}{\partial q_i}, t\right)~ $$ 其中 $S$ 是经典作用量，$H$ 是哈密顿函数（注意：此处不是算符）\(^\text{[26]: 308}\)。

　　 在哈密顿-雅可比方程中，广义坐标 $q_i$（$i = 1, 2, 3$）可以设定为笛卡尔坐标系中的位置坐标，即： $$ \mathbf{r} = (q_1, q_2, q_3) = (x, y, z)~ $$ 将波函数写作如下形式： $$ \Psi = \sqrt{\rho(\mathbf{r}, t)}\, e^{i S(\mathbf{r}, t) / \hbar}~ $$ 其中 $\rho$ 是概率密度函数。将这一表达式代入薛定谔方程，并对所得方程取极限 $\hbar \to 0$，就会得到哈密顿-雅可比方程。

5. 密度矩阵

　　 波函数并不总是描述量子系统及其行为最方便的方式。当一个系统的制备情况并不完全确定，或者当所研究的系统只是更大系统的一部分时，通常使用密度矩阵来代替 \(^\text{[26]: 74 }\)。密度矩阵是一个正半定算符，其迹等于 1（在希尔伯特空间为无限维时，也常称为 “密度算符”）。所有密度矩阵的集合构成一个凸集合，其极点是将希尔伯特空间中的矢量投影成算符的形式。 这些极点就是波函数的密度矩阵表示形式，用狄拉克记号表示为： $$ \hat{\rho} = |\Psi\rangle \langle \Psi|~ $$ 密度矩阵对应于波函数薛定谔方程的形式为 \(^\text{[27][28] }\)： $$ i\hbar \frac{\partial \hat{\rho}}{\partial t} = [\hat{H}, \hat{\rho}]~ $$ 其中中括号 $[\, ,\,]$ 表示对易子。 这个方程被称为：冯·诺依曼方程，或刘维尔–冯·诺依曼方程，也常被简称为密度矩阵的薛定谔方程 \(^\text{[26]: 312  }\)。如果哈密顿算符 $\hat{H}$ 与时间无关，该方程的解可写为 $$ \hat{\rho}(t) = e^{-i\hat{H}t/\hbar} \hat{\rho}(0)\, e^{i\hat{H}t/\hbar}~ $$ 更一般地，如果一个幺正算符 $\hat{U}(t)$ 描述了波函数在某时间区间内的演化，那么在同一时间区间内密度矩阵的演化形式为： $$ \hat{\rho}(t) = \hat{U}(t)\, \hat{\rho}(0)\, \hat{U}^\dagger(t)~ $$ 在这种幺正演化过程中，密度矩阵的冯·诺依曼熵保持不变 \(^\text{[26]: 267   }\)。

6. 相对论量子物理与量子场论

　　 前文所述的单粒子薛定谔方程主要适用于非相对论领域。其中一个原因是，它在本质上在伽利略变换下保持不变，而伽利略变换正是牛顿力学的对称群 \(^\text{[note 2]}\)。此外，在相对论框架下，粒子数发生变化是一种自然现象，因此一个只描述单个粒子（或固定数量粒子）的方程用途是有限的 \(^\text{[30]}\)。在更广义的框架中，薛定谔方程可以推广到适用于相对论情况，这需要借助于量子场论（QFT），它是一种将量子力学与狭义相对论结合的理论框架。在量子力学与相对论同时适用的区域，可以用相对论量子力学来描述。这类描述可以像薛定谔图像一样，使用由哈密顿算符生成的时间演化，例如在薛定谔泛函方法中所采用的做法 \(^\text{[31][32][33][34]}\)。

克莱因–戈尔登方程与狄拉克方程

　　 将量子物理与狭义相对论结合的尝试，最初是通过将相对论的能量–动量关系： $$ E^2 = (pc)^2 + (m_0 c^2)^2~ $$ 代替非相对论的能量公式来构造相对论波动方程的。这一思路产生了两个著名的方程：克莱因–戈尔登方程和狄拉克方程。

　　 其中，克莱因–戈尔登方程为： $$ -\frac{1}{c^2} \frac{\partial^2}{\partial t^2} \psi + \nabla^2 \psi = \frac{m^2 c^2}{\hbar^2} \psi~ $$ 克莱因–戈尔登方程是最早得到的相对论波动方程，甚至早于非相对论的单粒子薛定谔方程。它适用于具有质量的无自旋粒子。

　　 在历史上，狄拉克方程由保罗·狄拉克提出。他的目标是寻找一个在时间和空间上都是一阶导数的微分方程，这种形式对于相对论理论而言是非常理想的。要实现这一点，就必须对克莱因–戈尔登方程左边的算符进行 “开平方” 处理，也就是将其因式分解为两个算符的乘积。狄拉克用 $4 \times 4$ 的矩阵 $\alpha_1, \alpha_2, \alpha_3, \beta$ 表示这些因子。

　　 因此，波函数也变成了一个具有四个分量的函数，其演化遵循如下的狄拉克方程（在自由空间中的形式）： $$ \left( \beta m c^2 + c \sum_{n=1}^3 \alpha_n p_n \right) \psi = i \hbar \frac{\partial \psi}{\partial t}~ $$ 这个形式仍然类似于薛定谔方程，即：波函数的时间导数由一个哈密顿算符作用在波函数上所给出。

　　 如果要考虑外部作用力的影响，需要对哈密顿算符进行修正。例如，对于一个质量为 $m$、电荷为 $q$ 的粒子处于一个电磁场中（由电磁势 $\varphi$ 和 $\mathbf{A}$ 描述），其狄拉克哈密顿算符为： $$ \hat{H}_{\text{Dirac}} = \gamma^0 \left[ c\, \boldsymbol{\gamma} \cdot (\hat{\mathbf{p}} - q \mathbf{A}) + m c^2 + \gamma^0 q \varphi \right]~ $$ 其中，$\boldsymbol{\gamma} = (\gamma_1, \gamma_2, \gamma_3)$ 和 $\gamma^0$ 是狄拉克伽马矩阵，它们与粒子的自旋有关。狄拉克方程适用于所有自旋为 $1/2$ 的粒子。它的解是具有四个分量的旋量场，其中两个分量对应于粒子，另外两个分量对应于反粒子。

　　 对于克莱因–戈尔登方程来说，使用薛定谔方程的一般形式并不方便，在实际中，其哈密顿量也不会像狄拉克方程那样以类似的方式表达。对于相对论量子场的方程（克莱因–戈尔登方程和狄拉克方程就是两个例子），人们通常采用其他方法来推导，例如：从拉格朗日密度出发，通过场的欧拉–拉格朗日方程推导运动方程；或者使用洛伦兹群的表示理论，其中某些表示可用于确定给定自旋（与质量）自由粒子的波动方程。

　　 一般而言，要代入薛定谔方程的一般形式中的哈密顿量，不仅是位置算符和动量算符（以及可能的时间）组成的函数，还涉及自旋矩阵。此外，对于自旋为 $s$ 的有质量粒子，相对论波动方程的解是复值的 $2(2s+1)$ 分量旋量场。

福克空间

　　 最初形式的狄拉克方程，与单粒子薛定谔方程一样，是描述单个量子粒子的方程，波函数为 $\Psi(x, t)$。但在相对论量子力学中，粒子数并不是固定的，这限制了其适用性。从直观上看，这一复杂性可以通过质能等价原理来理解：能量可以转化为物质粒子，因此粒子可以从能量中产生。在量子场论（QFT）中，常见的做法是引入一个希尔伯特空间，其基态由粒子数标记，这就是所谓的福克空间。在该空间中，可以对量子态应用薛定谔方程 \(^\text{[30]}\)。然而，由于薛定谔方程明确选定了一个优先的时间轴，这使得理论的洛伦兹协变性不再显然成立。因此，在相对论性框架中，人们往往采用其他形式来构造理论 \(^\text{[35]}\)。

7. 历史

　　 在马克斯·普朗克对光进行量子化处理之后（参见黑体辐射），阿尔伯特·爱因斯坦将普朗克的能量子解释为光子，即光的粒子，并提出光子的能量与其频率成正比，这被认为是波粒二象性最早的迹象之一。由于在狭义相对论中，能量与动量的关系与频率与波数的关系相同，因此可以推导出光子的动量 $p$ 与其波长 $\lambda$ 成反比，或与波数 $k$ 成正比： $$ p = \frac{h}{\lambda} = \hbar k~ $$ 其中，$h$ 是普朗克常数，$\hbar = \frac{h}{2\pi}$ 是约化普朗克常数。

　　 路易·德布罗意提出：这一关系不仅适用于光子，也适用于所有粒子，包括有质量的粒子如电子。他证明，如果物质波与其对应的粒子一起传播，那么电子会形成驻波，意味着电子绕原子核运动时，只允许某些离散的角频率 \(^\text{[36]}\)。这些量子化的轨道就对应于离散的能级，德布罗意由此成功地再现了玻尔模型中的能级公式。玻尔模型基于对角动量 $L$ 的量子化假设： $$ L = n \frac{h}{2\pi} = n\hbar~ $$ 根据德布罗意的说法，电子由波来描述，而电子轨道的圆周长度上必须正好容纳一个整数个波长： $$ n\lambda = 2\pi r~ $$ 这一方法实质上将电子波限制在一维空间内，即一个半径为 $r$ 的圆形轨道上。

　　 早在德布罗意之前的 1921 年，芝加哥大学的阿瑟·C·伦恩就已经利用相对论能量-动量四矢量的完备性，推导出了我们今天称之为德布罗意关系式的内容 \(^\text{[37][38]}\)。

　　 不同于德布罗意，伦恩进一步推导了一个微分方程（很可能是将经典的亥姆霍兹方程与德布罗意关系 $p = \hbar k$ 和 $E = \hbar \omega$ 相结合而得出），这个方程后来被称为薛定谔方程，他还对氢原子求解了其能量本征值；然而，据卡门所述，该论文被《物理评论》拒绝发表 \(^\text{[39]}\)。

　　 在德布罗意思想的基础上，物理学家彼得·德拜随口评论说：如果粒子确实表现为波动，它们应该满足某种波动方程。受到德拜这句话的启发，薛定谔决心为电子寻找一个合适的三维波动方程。在这一过程中，他受到威廉·罗恩·哈密顿提出的力学与光学之间的类比的启发：在零波长极限下，几何光学的行为类似于经典力学系统——光线的轨迹变得清晰可见，并遵循费马原理，而这正是最小作用量原理的一个光学类比 \(^\text{[40]}\)。

　　 他发现的那个方程是：\(^\text{[41]}\) $$ i\hbar \frac{\partial}{\partial t} \Psi(\mathbf{r}, t) = -\frac{\hbar^2}{2m} \nabla^2 \Psi(\mathbf{r}, t) + V(\mathbf{r}) \Psi(\mathbf{r}, t).~ $$ 此时，阿诺德·索末菲已经通过加入相对论修正完善了玻尔模型。[42][43]薛定谔利用相对论的能量-动量关系，在库仑势下推导出了现在被称为克莱因–戈尔登方程的形式（在自然单位制下）： $$ \left(E + \frac{e^2}{r}\right)^2 \psi(x) = -\nabla^2 \psi(x) + m^2 \psi(x).~ $$ 他找到了这个相对论方程的驻波解，但这些相对论修正结果与索末菲公式不一致。感到沮丧的他放下了这些计算，并在 1925 年 12 月带着情妇隐居到了山区小屋中。\(^\text{[44]}\)

　　 在山中小屋时，薛定谔决定将他早期的非相对论计算结果发表，认为它们已经足够新颖，而暂时放弃继续处理相对论修正的问题。尽管求解氢原子的微分方程存在困难（他曾向数学家好友赫尔曼·外尔求助 \(^\text{[45]: 3}\) ），薛定谔还是在 1926 年发表的论文中表明，他的非相对论波动方程可以正确导出氢原子的光谱能级。\(^\text{[45]: 1 [46]}\) 薛定谔将氢原子中的电子视作一个波 $\Psi(\mathbf{x}, t)$，在由质子产生的势阱 $V$ 中运动。这样的计算准确地重现了玻尔模型中的能级结构。

　　 薛定谔方程详细描述了 $\Psi$ 的行为，但并没有说明 $\Psi$ 的物理本质。 薛定谔最初尝试将 $\Psi \frac{\partial \Psi^*}{\partial t}$ 的实部解释为电荷密度，后来在下一篇论文中修正这一观点，改为认为 $|\Psi|^2$ 是电荷密度。但这一解释最终并不成功。\(^\text{[note 3]}\)

　　 1926 年，在该论文发表后仅数日，马克斯·玻恩成功地将 $\Psi$ 解释为概率幅，其模的平方 $|\Psi|^2$ 就是概率密度。\(^\text{[47]: 220}\) 

　　 薛定谔本人后来如此解释这一概率解释：\(^\text{[50]}\)

　　 “此前提到的 psi 函数……现在被用来预测测量结果的概率。在其中，包含了基于理论对未来可测结果的期望总和，就像列在一本目录中的那样。”

　　 —— 欧文·薛定谔

8. 诠释

　　 薛定谔方程提供了一种方法，用于计算一个系统的波函数及其如何随时间动态演化。然而，薛定谔方程本身并未直接说明波函数究竟是什么。对薛定谔方程的意义以及方程中数学实体如何对应于物理现实的理解，取决于你所采纳的量子力学诠释。

　　 在通常被归为哥本哈根诠释的一系列观点中，一个系统的波函数被认为是关于该系统的统计信息的集合。薛定谔方程用来关联系统在某一时刻的信息与另一时刻的信息。尽管由薛定谔方程描述的时间演化过程是连续且确定性的（即只要已知某一时刻的波函数，就可原则上计算出所有未来时刻的波函数），但在测量过程中，波函数也可能以不连续且随机的方式发生变化。按照这种观点，波函数的变化是因为获得了新的信息。测量之后的波函数通常无法在测量前知道，但可以通过玻恩规则计算出不同可能性的概率 \(^\text{[26][51][note 4]}\)。一些较新的量子力学诠释，例如关系量子力学和 QBism（量子贝叶斯主义），也赋予薛定谔方程类似的地位 \(^\text{[54][55]}\)。

　　 薛定谔本人在 1952 年曾建议，在薛定谔方程下演化的一个叠加态的不同项 “并不是互斥的选项，而是全部真的同时发生了”。这一观点被解读为对后来埃弗雷特多世界诠释（的早期预示 \(^\text{[56][57][note 5]}\)。这一诠释于 1956 年被独立提出，主张：量子理论描述的所有可能性都同时在一个由大量独立平行宇宙组成的多重宇宙中发生 \(^\text{[59]}\)。这种诠释取消了波函数塌缩的公设，只保留薛定谔方程下的连续演化，因此所有可能的被测系统状态、测量装置状态以及观察者状态都实际存在于一个真实的物理量子叠加态中。虽然整个多重宇宙是决定性的，但我们感知到的行为是非决定性的，由概率支配，这是因为我们无法观测整个多重宇宙，而只能看到其中一个平行宇宙。具体这个过程如何运作一直存在许多争议。比如：我们为何要对那些在某些世界中必然发生的结果赋予概率？又为何这些概率应由玻恩规则给出？\(^\text{[60]}\) 已有一些尝试在多世界框架下回答这些问题，但目前尚无共识认为这些解释完全成立 \(^\text{[61][62][63]}\)。

　　 玻姆力学则是将量子力学重新表述为一个决定性理论，代价是引入了一种源自 “量子势” 的力。在该理论中，每个物理系统不仅具有一个波函数，还具有一个真实的位置，其随时间的演化遵循一个非局域的导引方程。一个物理系统的演化始终由薛定谔方程联合导引方程所决定 \(^\text{[64]}\)。

9. 参见

• 埃克豪斯方程
• 福克–普朗克方程
• 量子力学的诠释
• 以埃尔温·薛定谔命名的事物列表
• 对数型薛定谔方程
• 非线性薛定谔方程
• 泡利方程
• 量子通道
• 薛定谔方程与路径积分形式的关系
• 薛定谔绘景
• 维格纳拟概率分布

10. 注释

1. 从态矢量中获得概率的这一规则意味着：仅在整体相位上有差异的两个矢量是物理上等价的；也就是说，$|\psi\rangle$ 和 $e^{i\alpha}\psi\rangle$ 表示相同的量子态。换句话说，所有可能的量子态是在希尔伯特空间的射影空间中的点，通常称为射影希尔伯特空间。
2. 更准确地说，薛定谔方程在进行伽利略变换之后，可以通过对波函数施加一个整体相位变换来抵消其影响，从而使得通过玻恩规则计算得到的概率不变 \(^\text{[29]}\)。
3. 详见 Moore\(^\text{[47]：219}\)、Jammer\(^\text{[48]：24–25}\)、以及 Karam\(^\text{[49]}\)。
4. 关于 “哥本哈根诠释” 的哲学立场有一个难点，即没有单一权威的来源明确定义该诠释的具体内容。另一难点是：爱因斯坦、玻尔、海森堡等人熟悉的哲学背景，对于今天的物理学家，甚至是物理哲学家来说，已不再熟悉 \(^\text{[52][53]}\)。
5. 薛定谔的后期著作中也包含与模态诠释类似的观点，该诠释最早由巴斯·范·弗拉森提出。由于薛定谔接受一种后马赫式的中立一元论——其中 “物质” 和 “意识” 只是同一基础元素的不同表现或排列，因此将波函数看作物理实体或看作信息，本质上可以互换 \(^\text{[58]}\)。

11. 参考文献

1. Griffiths, David J. (2004).《量子力学导论》（第 2 版）. Prentice Hall. ISBN 978-0-13-111892-8.
2. “物理学家埃尔温·薛定谔的谷歌涂鸦纪念其在量子力学方面的贡献”. 《卫报》. 2013 年 8 月 13 日. 取自 2013 年 8 月 25 日.
3. Schrödinger, E. (1926). “原子与分子的波动理论” [An Undulatory Theory of the Mechanics of Atoms and Molecules] (PDF).《物理评论》, 28 (6): 1049–1070. Bibcode:1926PhRv...28.1049S. doi:10.1103/PhysRev.28.1049. 原文 PDF 存档于 2008 年 12 月 17 日.
4. Whittaker, Edmund T. (1989).《以太与电学理论史（第二卷）：现代理论，1900–1926》. New York: Dover Publications. ISBN 978-0-486-26126-3.
5. Zwiebach, Barton (2022).《掌握量子力学：基础、理论与应用》. MIT 出版社. ISBN 978-0-262-04613-8. OCLC 1347739457.
6. Dirac, Paul Adrien Maurice (1930).《量子力学原理》. 牛津：Clarendon 出版社.
7. Hilbert, David (2009). 由 Tilman Sauer 与 Ulrich Majer 编辑.《物理学基础讲义 1915–1927：相对论、量子理论与认识论》. Springer 出版社. doi:10.1007/b12915. ISBN 978-3-540-20606-4. OCLC 463777694.
8. von Neumann, John (1932).《量子力学的数学基础》. 柏林：Springer. 英文译本：Mathematical Foundations of Quantum Mechanics. 由 Robert T. Beyer 翻译. 普林斯顿大学出版社, 1955 年.
9. Weyl, Hermann (1950) [原作 1931].《群论与量子力学》. H. P. Robertson 翻译. Dover 出版社. ISBN 978-0-486-60269-1. 原著德文名为《Gruppentheorie und Quantenmechanik》（第 2 版），由 S. Hirzel Verlag 出版.
10. Hall, B. C. (2013). “第六章：关于谱定理的不同视角”. 载于《数学家的量子理论》. 数学研究生教材系列（Graduate Texts in Mathematics）第 267 卷. Springer 出版社. Bibcode:2013qtm..book.....H. ISBN 978-1461471158.
11. Cohen-Tannoudji, Claude；Diu, Bernard；Laloë, Franck（2005）。《量子力学》。Susan Reid Hemley、Nicole Ostrowsky 和 Dan Ostrowsky 翻译。约翰·威利父子公司（John Wiley & Sons）。ISBN 0-471-16433-X。
12. Shankar, R.（1994）。《量子力学原理》（第 2 版）。Kluwer Academic/Plenum 出版社。ISBN 978-0-306-44790-7。
13. Rieffel, Eleanor G.；Polak, Wolfgang H.（2011 年 3 月 4 日）。《量子计算导论》。麻省理工学院出版社。ISBN 978-0-262-01506-6。
14. Yaffe, Laurence G.（2015）。《第 6 章：对称性》（PDF）。《物理 226：粒子与对称性》。2021 年 1 月 1 日检索。
15. Sakurai, J. J.；Napolitano, J.（2017）。《现代量子力学》（第 2 版）。剑桥大学出版社，第 68 页。ISBN 978-1-108-49999-6。OCLC 1105708539。
16. Ashcroft, Neil W.；Mermin, N. David（1976）。《固体物理》。Harcourt College Publishers。ISBN 0-03-083993-9。
17. Sakurai, Jun John；Napolitano, Jim（2021）。《现代量子力学》（第 3 版）。剑桥大学出版社。ISBN 978-1-108-47322-4。
18. Mostafazadeh, Ali（2003 年 1 月 7 日）。《Klein–Gordon 类型演化方程解空间上的希尔伯特空间结构》。《经典与量子引力》，20（1）：155–171。arXiv\:math-ph/0209014。Bibcode:2003CQGra..20..155M。doi:10.1088/0264-9381/20/1/312。ISSN 0264-9381。
19. Singh, Chandralekha（2008 年 3 月）。《研究生初期对量子力学的理解》。美国物理学杂志，76（3）：277–287。arXiv:1602.06660。Bibcode:2008AmJPh..76..277S。doi:10.1119/1.2825387。ISSN 0002-9505。S2CID 118493003。
20. Adams, C.S；Sigel, M；Mlynek, J（1994）。《原子光学》。《物理报告》，240（3）：143–210。Elsevier BV。Bibcode:1994PhR...240..143A。doi:10.1016/0370-1573(94)90066-3。ISSN 0370-1573。
21. Atkins, P. W.（1978）。《物理化学》。牛津大学出版社。ISBN 0-19-855148-7。
22. Hook, J. R.；Hall, H. E.（2010）。《固体物理学》。曼彻斯特物理系列（第 2 版）。John Wiley & Sons。ISBN 978-0-471-92804-1。
23. Townsend, John S.（2012）。《第 7 章：一维谐振子》。载于《现代量子力学方法》。University Science Books，页 247–250，254–255，257，272。ISBN 978-1-891389-78-8。
24. Tipler, P. A.；Mosca, G.（2008）。《科学家与工程师的物理学——含现代物理》（第 6 版）。Freeman。ISBN 978-0-7167-8964-2。
25. Griffiths, David J.（2008）。《基本粒子导论》。Wiley-VCH，页 162 起。ISBN 978-3-527-40601-2。2011 年 6 月 27 日检索。
26. Peres, Asher（1993）。《量子理论：概念与方法》。Kluwer。ISBN 0-7923-2549-4。OCLC 28854083。
27. Breuer, Heinz；Petruccione, Francesco（2002）。《开放量子系统理论》。牛津大学出版社，第 110 页。ISBN 978-0-19-852063-4。
28. Schwabl, Franz（2002）。《统计力学》。施普林格出版社，第 16 页。ISBN 978-3-540-43163-3。
29. Home, Dipankar（2013）。《量子物理的概念基础》。Springer US，第 4–5 页。ISBN 9781475798081。OCLC 1157340444。
30. Coleman, Sidney（2018 年 11 月 8 日）。Derbes, David；Ting, Yuan-sen；Chen, Bryan Gin-ge；Sohn, Richard；Griffiths, David；Hill, Brian（编）。《Sidney Coleman 的量子场论讲座》。世界科技出版社。ISBN 978-9-814-63253-9。OCLC 1057736838。
31. Symanzik, K.（1981 年 7 月 6 日）。《可重整量子场论中的薛定谔表象与卡西米尔效应》。《核物理 B》，190（1）：1–44。Bibcode:1981NuPhB.190....1S。doi:10.1016/0550-3213(81)90482-X。ISSN 0550-3213。
32. Kiefer, Claus（1992 年 3 月 15 日）。《标量量子电动力学的泛函薛定谔方程》。《物理评论 D》，45（6）：2044–2056。Bibcode:1992PhRvD..45.2044K。doi:10.1103/PhysRevD.45.2044。ISSN 0556-2821。PMID 10014577。
33. Hatfield, Brian（1992）。《点粒子与弦的量子场论》。马萨诸塞州剑桥：Perseus Books。ISBN 978-1-4294-8516-6。OCLC 170230278。
34. Islam, Jamal Nazrul（1994 年 5 月）。《量子场论中的薛定谔方程》。《物理学基础》，24（5）：593–630。Bibcode:1994FoPh...24..593I。doi:10.1007/BF02054667。ISSN 0015-9018。S2CID 120883802。
35. Srednicki, Mark Allen（2012）。《量子场论》。剑桥：剑桥大学出版社。ISBN 978-0-521-86449-7。OCLC 71808151。
36. 德布罗意（de Broglie, L.）（1925）。《关于量子理论的研究》（法文原文：Recherches sur la théorie des quanta）。《物理年鉴》（法文），第 10 卷第 3 期，第 22–128 页。Bibcode:1925AnPh...10...22D。doi:10.1051/anphys/192510030022。原文（PDF）存档于 2009 年 5 月 9 日。
37. Weissman, M. B.；V. V. Iliev；I. Gutman（2008）。《一位先驱的回忆：关于阿瑟·康斯坦特·朗的传记笔记》（PDF）刊载于《数学与计算化学通讯》，第 59 卷第 3 期，第 687–708 页。
38. Samuel I. Weissman；Michael Weissman（1997）。《阿兰·索卡尔的骗局与朗的量子力学理论》。刊于《今日物理》，第 50 卷第 6 期，第 15 页。Bibcode:1997PhT....50f..15W。doi:10.1063/1.881789。
39. Kamen, Martin D.（1985）。《光辉的科学，黑暗的政治》。加利福尼亚大学出版社，第 29–32 页。ISBN 978-0-520-04929-1。
40. 薛定谔（1984）。《论文集》。Friedrich Vieweg und Sohn 出版社。ISBN 978-3-7001-0573-2。见 1926 年第一篇论文的引言。
41. Lerner, R. G.；Trigg, G. L.（1991）。《物理百科全书》（第 2 版）。VHC 出版社。ISBN 0-89573-752-3。
42. 索末菲尔德（Sommerfeld, A.）（1919）。《原子结构与谱线》（德文：*Atombau und Spektrallinien*）。不伦瑞克：Friedrich Vieweg und Sohn 出版社。ISBN 978-3-87144-484-5。
43. 英文资料来源见：T. Haar（1967）。《旧量子理论》。牛津与纽约：Pergamon 出版社。
44. Teresi, Dick（1990 年 1 月 7 日）。《量子力学的孤独游侠》。刊于《纽约时报》。ISSN 0362-4331。检索日期：2020 年 10 月 13 日。
45. 薛定谔，Erwin（1982）。《波动力学论文集》（第 3 版）。美国数学学会。ISBN 978-0-8218-3524-1。
46. 薛定谔（1926）。《量子化作为本征值问题》。《物理年鉴》（德文：Annalen der Physik），第 384 卷第 4 期，第 361–377 页。Bibcode:1926AnP...384..361S。doi:10.1002/andp.19263840404。
47. Moore, W. J.（1992）。《薛定谔：生命与思想》。剑桥大学出版社。ISBN 978-0-521-43767-7。
48. Jammer, Max（1974）。《量子力学的哲学：量子力学诠释的历史透视》。Wiley-Interscience 出版社。ISBN 9780471439585。
49. Karam, Ricardo（2020 年 6 月）。《薛定谔最初对复数波函数的困惑》。刊载于《美国物理杂志》，第 88 卷第 6 期，第 433–438 页。Bibcode:2020AmJPh..88..433K。doi:10.1119/10.0000852。ISSN 0002-9505。S2CID 219513834。
50. Erwin Schrödinger，《量子力学的现状》，第 9 页（共 22 页）。英文版由 John D. Trimmer 翻译，首次发表于《美国哲学学会会刊》，第 124 卷，第 323–338 页。随后收录于 J. A. Wheeler 与 W. H. Zurek 主编的《量子理论与测量》第一部分第 I.11 节，普林斯顿大学出版社，1983 年，新泽西，ISBN 0691083169。
51. Omnès, R.（1994）。《量子力学的诠释》。普林斯顿大学出版社。ISBN 978-0-691-03669-4。OCLC 439453957。
52. Faye, Jan（2019）。《量子力学的哥本哈根诠释》，载于 Edward N. Zalta 主编，《斯坦福哲学百科全书》，斯坦福大学形而上学研究实验室。
53. Chevalley, Catherine（1999）。《为什么我们觉得玻尔晦涩难懂？》，载于 Daniel Greenberger、Wolfgang L. Reiter、Anton Zeilinger 主编的《量子物理的认识论与实验视角》，Springer Science+Business Media，第 59–74 页。doi:10.1007/978-94-017-1454-9。ISBN 978-9-04815-354-1。
54. van Fraassen, Bas C.（2010 年 4 月）。《罗维利的世界》，刊于《物理学基础》，第 40 卷第 4 期，第 390–417 页。Bibcode:2010FoPh...40..390V。doi:10.1007/s10701-009-9326-5。ISSN 0015-9018。S2CID 17217776。
55. Healey, Richard（2016）。《量子贝叶斯主义与实用主义的量子理论观点》，载于 Edward N. Zalta 主编，《斯坦福哲学百科全书》，斯坦福大学形而上学研究实验室。
56. Deutsch, David（2010）。《超越宇宙》。载于 S. Saunders、J. Barrett、A. Kent、D. Wallace 主编，《多重世界？埃弗里特、量子理论与现实》，牛津大学出版社。
57. Schrödinger, Erwin（1996）。由 Michel Bitbol 编辑。《量子力学的诠释：都柏林研讨会（1949–1955）及其他未发表论文》。OxBow 出版社。
58. Bitbol, Michel（1996）。《薛定谔的量子力学哲学》。多德雷赫特：Springer 荷兰分社。ISBN 978-94-009-1772-9。OCLC 851376153。
59. Barrett, Jeffrey（2018）。《埃弗里特的相对状态表述的量子力学》，载于 Edward N. Zalta 主编，《斯坦福哲学百科全书》，斯坦福大学形而上学研究实验室。