厦门大学 2011 年硕士入学物理考试试题

                     

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 跳伞运动员初张伞时(设此初始时刻 $t=0$)的速度为 $v_0$。已知下降过程中阻力大小与速度平方成正比，比例系数为 $a$。若人伞总质量为 $m$，求跳伞运动员的速度随时间变化的函数。
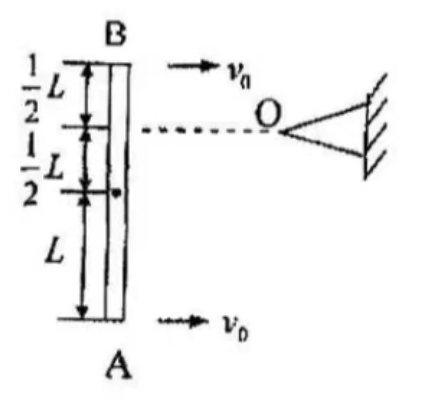
2. -匀质细棒长为 $ 2L$，质量为 $m$，以与棒长方向相垂直的速度 $v_0$ 在光滑水平面内平动时，与前方一固定的光滑支点 O 发生完全非弹性碰撞。碰撞点位于棒中心的一方 $\frac{1}{2}L$ 处，如图所示。求棒在碰撞后的瞬时绕 O 点转动的角速度 $\omega$。(已知长度为 $l$，质量为 $m$ 的均匀细棒绕通过其端点且与其垂直的轴转动时的转动惯量 $J=\frac{1}{3}ml^2$)
   
   图 1
3. 容器中储存有由 $16$ 克氧气和 $4$ 克氦气组成的混合气体，系统的压强为 $\rho=1.0*10^5Pa$，温度 $T=300K$。已知气体普适常量 $R=8.31J/(mo1.K)$，氧气和氦气的分子量分别为 32 和 4，试计算:
   (1)系统的内能;
   (2)该混合气体的定容摩尔热容；
   (3)混合气体分子的方均根速率。
4. 已知大气压强为 $l$ 高的水银柱，水银的密度为 $\rho$。一粗细均匀的刚性细管出长度均为 $l$ 的两部分组成，其中一部分沿水平方向，另一部分沿竖直方向，有一段长度为 $l/2$ 的水银柱，开始时，水银柱刚好位于细管水平部分的右半部并处于平衡状态，被封闭的气柱长度为 $l/2$，如图所示。现使气柱中的气体缓慢膨胀，直到水银从细管的开口端全部逸出为止。
   (1)求整个过程中封闭气柱中的气体压强 $\rho$ 与气柱长度 $x$ 的函数关系;
   (2)已知封闭气柱中气体的定容摩尔热容 $C_{F,m}=\frac{3}{2}R$，其中 $R$ 为气体普适常量，求在整个过程中封闭气柱中的气体与外界交换的热量(忽略水银柱与气之间的热交换 )。
5. 电荷 $Q$ 均匀分布在半径为 $R$ 的球体内，求其电场能量。
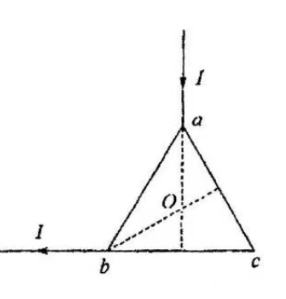
6. 粗细均匀的金属导线构成如图线框,中间为正三角形 $abc$,电流 $I$ 从无限远处沿垂直于 $bc$ 的方向从 $a$ 端流入，从 $b$ 端沿 $cb$ 方向流向无限远处，三角形边长为 $l$，求三角形中心点 $O$ 处的磁感应强度。
   
   图 2
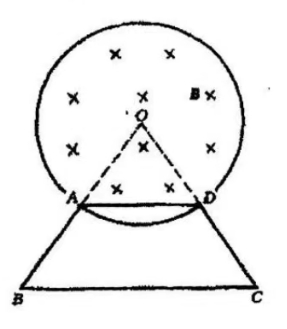
7. 在半径为 $a$ 的细长螺线管中，磁场随时间的变化率为 $ \frac{\mathrm{d}{B}}{\mathrm{d}{t}} $ 且 $ \frac{\mathrm{d}{B}}{\mathrm{d}{t}} $>0，一直导线驾成等腰梯形闭合回路 $ABCD$，上下底分别长为 $a$ 和 $2a$ 放置如图，求梯形各边以及整个回路的感应电动势。
   
   图 3