图论（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

图
图 1：一个具有 6 个顶点和 7 条边的图

　　 在数学和计算机科学中，图论是对图的研究。图是一种数学结构，用于刻画对象之间的成对关系。在这一语境下，一个图由顶点（亦称为节点或点）组成，顶点之间通过边（亦称为弧、链接或线）连接。图论中区分无向图与有向图：在无向图中，边对两个顶点的连接是对称的；而在有向图中，边对两个顶点的连接是不对称的。图是离散数学研究的主要对象之一。

1. 定义

　　 图论中的定义不尽相同。以下是一些更基本的定义图及其相关数学结构的方式。

图

图
图 2：一个具有三个顶点和三条边的无向图。

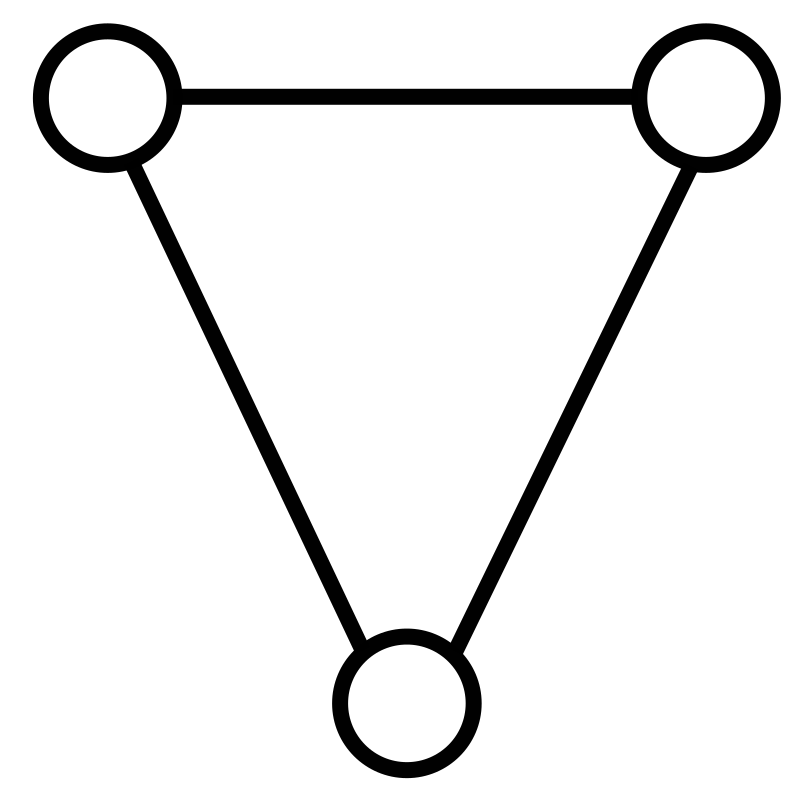
　　 在一个受限但非常常见的意义下，\(^\text{[1][2]}\) 图是一个有序对 $G = (V, E)$ 其中：

　　 为了避免歧义，这类对象可称为无向单图。

　　 在边 ${x, y}$ 中，顶点 $x$ 与 $y$ 称为该边的端点。该边被认为连接 $x$ 与 $y$，并与 $x$、$y$ 关联。图中可能存在某些顶点没有属于任何边。根据该定义，不允许出现多重边（即两条或以上的边连接相同的一对顶点）。

图
图 3：一个具有 3 个顶点、3 条边和 4 条自环的无向多重图示例。

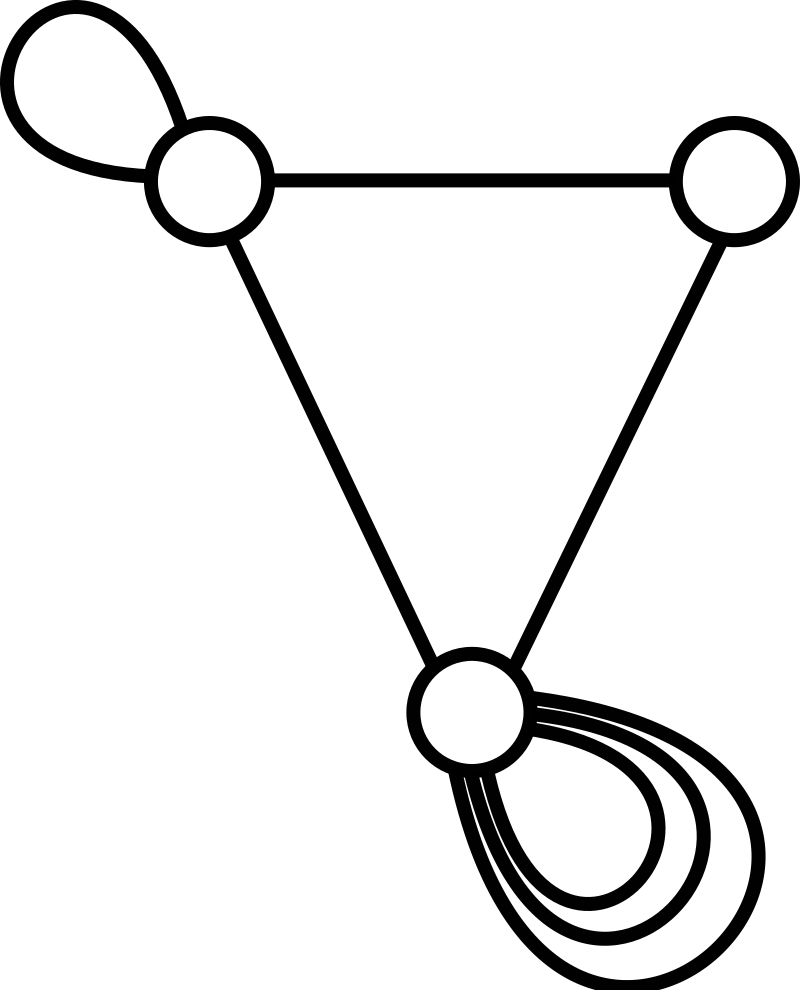
　　 在另一种更一般的意义下，允许多重边，\(^\text{[3][4]}\) 图是一个有序三元组 $G = (V, E, \phi)$ 其中：

　　 为了避免歧义，这类对象可称为无向多重图。

　　 自环是一条将顶点连接到其自身的边。在前述两种定义下，图都不能有自环。因为一条将顶点 $x$ 与自身连接的自环对应的边为 ${x,x} = {x}$，而它并不属于 ${{x,y}\mid x,y \in V, x \neq y}$。若要允许自环，则必须扩展定义：对于无向单图，其边集应修改为 $E \subseteq {{x,y}\mid x,y \in V}$；对于无向多重图，其关联函数应修改为 $\phi : E \to {{x,y}\mid x,y \in V}$。为了避免歧义，这些类型的对象可分别称为允许自环的无向单图和允许自环的无向多重图（有时也称为无向伪图 pseudograph）。

　　 通常情况下，$V$ 和 $E$ 被认为是有限的；许多著名的结论在无限图中并不成立（或有所不同），因为许多推理在无限情形下失效。此外，通常假设 $V$ 是非空的，但 $E$ 可以是空集。图的阶是 $|V|$，即其顶点数。图的大小是 $|E|$，即其边数。一个顶点的度（degree 或 valency）是与其关联的边的条数，其中自环计作两次。图的度是所有顶点度数的最大值。

　　 在一个阶为 $n$ 的无向单图中，每个顶点的最大度为 $n-1$，该图的最大边数为 $\frac{n(n-1)}{2}$.

　　 允许自环的无向单图 $G$ 的边集，在其顶点集上诱导出一个对称齐次关系 $\sim$，称为 $G$ 的邻接关系。具体而言，对于每条边 $(x, y)$，其端点 $x$ 和 $y$ 被称为邻接，记作 $x \sim y$.

有向图

图
图 4：一个具有三个顶点和四条有向边的有向图（双箭头表示在两个方向上各有一条边）。

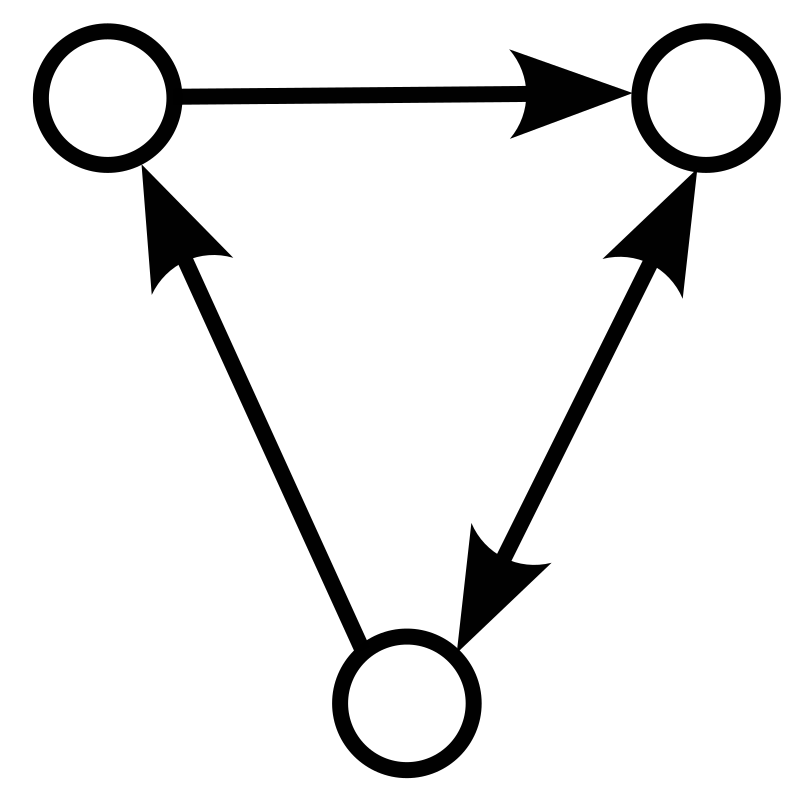
　　 有向图（directed graph 或 digraph）是一种边具有方向性的图。在一个受限但非常常见的意义下，\(^\text{[5]}\) 有向图是一个有序对 $G = (V, E)$ 其中：

　　 为了避免歧义，这类对象可称为有向单图。在集合论和图论中，$V^{n}$ 表示由集合 $V$ 中元素组成的 $n$ 元组的集合，即长度为 $n$ 的有序序列，序列中的元素不必两两不同。

　　 在一条从 $x$ 指向 $y$ 的边 $(x,y)$ 中：顶点 $x$ 和 $y$ 被称为该边的端点；$x$ 称为该边的尾，$y$ 称为该边的头；这条边被认为连接 $x$ 与 $y$，并且与 $x$、$y$ 关联。图中可能存在一些顶点并不属于任何边。边 $(y,x)$ 称为边 $(x,y)$ 的反向边。在上述定义下，不允许出现多重边，即尾和头都相同的两条或更多的边。

　　 在另一种更一般的意义下，允许多重边，\(^\text{[5]}\) 有向图是一个有序三元组 $G = (V, E, \phi)$ 其中：

　　 为了避免歧义，这类对象可称为有向多重图。

　　 自环是一条将顶点连接到其自身的边。在前述两种定义下的有向图中，自环是不允许的。因为一条将顶点 $x$ 与自身相连的自环对应的边为 $(x,x)$，但 $(x,x)$ 并不属于 ${(x,y)\mid (x,y)\in V^{2}, ; x \neq y}$.因此，为了允许自环，必须扩展定义：对于有向单图，其边集的定义应修改为 $E \subseteq {(x,y)\mid (x,y)\in V^{2}}$;对于有向多重图，其关联函数的定义应修改为 $\phi : E \to {(x,y)\mid (x,y)\in V^{2}}$.为了避免歧义，这些对象可分别称为：允许自环的有向单图和允许自环的有向多重图（或称 quiver，箭图）。

　　 允许自环的有向单 $G$ 的边集在其顶点集上诱导出一个齐次关系 $\sim$，称为 $G$ 的邻接关系。具体而言，对于每条边 $(x,y)$，其端点 $x$ 和 $y$ 被称为邻接，记作 $x \sim y$.

2. 应用

图
图 5：由维基百科编辑者（边）与不同语言版本的维基百科（顶点）在 2013 年夏季某一个月内的贡献所形成的网络图。\(^\text{[6]}\)

　　 图可以用来建模物理、生物学 \(^\text{[7][8]}\)、社会和信息系统 \(^\text{[9]}\) 中的多种关系与过程。许多实际问题都能用图来表示。为了强调它们在现实系统中的应用，网络这一术语有时被定义为：在图的顶点和边上附加属性（例如名称）的图。而把现实世界系统表达并理解为网络的学科被称为网络科学。

计算机科学

　　 在计算机科学中，“因果” 与 “非因果” 的链接结构就是用来表示通信网络、数据组织、计算设备、计算流程等的图。例如，一个网站的链接结构可以用有向图来表示，其中顶点（节点）代表网页，有向边代表从一个页面到另一个页面的超链接。类似的方法也可应用于社交媒体 \(^\text{[10]}\)、交通出行、生物学、芯片设计、神经退行性疾病进展的映射 \(^\text{[11][12]}\) 以及许多其他领域。因此，开发处理图的算法是计算机科学中的一个重要研究方向。图的变换常常被形式化为图重写系统。与专注于基于规则的图内存操作的图变换系统相互补充的是图数据库，它们致力于对图结构数据进行事务安全、持久化的存储与查询。

语言学

　　 图论方法以多种形式被证明在语言学中特别有用，因为自然语言往往很适合用离散结构来刻画。传统上，句法和组合语义学遵循基于树的结构，其表达能力依赖于组合性原则，并以层级化的图来建模。较为当代的方法，例如以词为中心的短语结构语法，则使用类型特征结构来建模自然语言的句法，而这类结构本质上是有向无环图。在词汇语义学中，尤其是在计算机应用中，若一个词的意义通过与相关词的关系来理解，其建模会更加容易；因此，语义网络在计算语言学中占有重要地位。除此之外，在音系学中（例如使用格图的最优化理论）以及形态学中（例如使用有限状态转换器的有限状态形态学），将语言分析为图的方式也十分常见。实际上，这一数学领域对语言学的价值催生了诸如 TextGraphs 这样的组织，以及一系列 “Net” 项目，例如 WordNet、VerbNet 等。

物理学与化学

　　 图论也被用于研究化学和物理中的分子。在凝聚态物理中，复杂的三维原子结构模拟可以通过收集与原子拓扑相关的图论性质的统计量来进行定量研究。与此同时，“费曼图及其计算规则以一种与实验数据密切相关的形式总结了量子场论”\(^\text{[13]}\)。在化学中，图为分子提供了一种自然的建模方式，其中顶点代表原子，边代表化学键。这种方法特别适用于分子结构的计算机处理，从化学编辑器到数据库搜索均有应用。在统计物理中，图可以表示系统中相互作用部分之间的局部连接，以及物理过程在这些系统中的动力学演化。类似地，在计算神经科学中，图可以用来表示大脑区域之间的功能连接，这些区域的相互作用产生各种认知过程，其中顶点表示不同的大脑区域，边表示这些区域之间的连接。图论在电学网络的建模中也扮演着重要角色：此时边带有权重，该权重与导线段的电阻相关，用于获得网络结构的电学性质 \(^\text{[14]}\)。此外，图还可用于表示多孔介质的微观通道，其中顶点代表孔隙，边代表连接孔隙的细小通道。化学图论使用分子图来对分子建模。图与网络是研究和理解相变与临界现象的极佳模型。移除节点或边会导致一个临界转变，使得网络破裂成更小的簇，这被视为一种相变。该现象通过渗流理论进行研究 \(^\text{[15]}\)。

社会科学

图
图 6：社会学中的图论：Moreno 社会图（1953）。[16]

　　 图论在社会学中也被广泛应用，例如用来衡量行动者的声望，或研究谣言传播，尤其是通过社会网络分析软件来实现。在社会网络这一范畴下，存在多种不同类型的图。\(^\text{[17]}\) 熟人图与朋友图：描述人们之间是否互相认识。影响图：建模某些人是否能够影响他人的行为。合作图：建模两个人是否以某种特定方式进行合作，例如共同出演一部电影。

生物学

　　 同样，图论在生物学和保护研究中也非常有用。在这种应用中，顶点可以表示某些物种存在（或栖息）的区域，边则表示区域之间的迁徙路径或移动。这类信息在研究繁殖模式，或追踪疾病、寄生虫传播，以及考察迁徙变化如何影响其他物种时，具有重要意义。

　　 图论还常用于分子生物学和基因组学，以建模和分析具有复杂关系的数据集。例如，在单细胞转录组分析中，基于图的方法常被用于将细胞 “聚类” 为不同的细胞类型。另一种应用是对通路中的基因或蛋白质建模，并研究它们之间的关系，如代谢通路和基因调控网络 \(^\text{[18]}\)。此外，进化树、生态网络以及基因表达模式的层次聚类也常用图结构来表示。

　　 图论还应用于连接组学 \(^\text{[19]}\)：神经系统可以看作一张图，其中节点是神经元，边则是它们之间的连接。

数学

　　 在数学中，图在几何学和拓扑学的某些部分（如结理论）中非常有用。代数图论与群论关系密切。代数图论已被应用于许多领域，包括动力系统和复杂性研究。

其他主题

　　 图结构可以通过为每条边赋予一个权重来扩展。带权图用于表示那些成对连接带有数值信息的结构。例如，如果图表示一个道路网络，边的权重可以表示每条道路的长度。每条边也可能带有多个权重，如距离（如前例所示）、行驶时间或金钱成本。这类带权图常用于 GPS 程序和旅行规划搜索引擎，例如比较航班时间和费用。

3. 历史

图
图 7：由维基百科编辑者（边）在 2013 年夏季某一个月内对不同语言版本的维基百科（顶点）所作贡献而形成的网络图。[6]

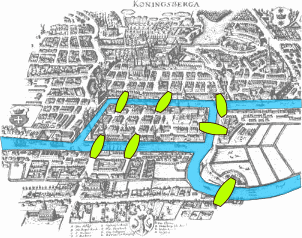
　　 莱昂哈德·欧拉于 1736 年发表的关于柯尼斯堡七桥问题的论文被认为是图论史上的第一篇论文。\(^\text{[20]}\) 这篇论文，以及范德蒙德关于骑士巡游问题的论文，延续了莱布尼茨开创的 analysis situs（位置分析）思路。欧拉提出的关于凸多面体的边数、顶点数与面数关系的公式后来被柯西 \(^\text{[21]}\) 和吕利耶 \(^\text{[22]}\) 研究并推广，这标志着后来被称为拓扑学的数学分支的开端。

　　 在欧拉的七桥论文发表一个多世纪之后，正值李斯廷引入拓扑学概念之际，凯莱因对微积分中出现的某些特殊解析形式的兴趣，促使他研究了一类特殊的图——树。\(^\text{[23]}\) 这一研究在理论化学中有着广泛的影响。他使用的技术主要涉及具有特定性质的图的枚举。枚举图论由此产生，既来源于凯莱的研究成果，也来源于波利亚在 1935 至 1937 年间发表的基本结果。这些结果又在 1959 年由德布鲁因推广。凯莱还将他在树方面的研究成果与当时关于化学组成的研究联系起来。\(^\text{[24]}\) 数学与化学思想的融合开启了如今已成为图论标准术语的一部分的研究传统。

　　 特别是，“图（” 这一术语由西尔维斯特在 1878 年发表在《自然》上的一篇论文中首次引入，他在其中将代数中的 “量纲不变量” 与 “协变式” 类比于分子图示：\(^\text{[25]}\)

　　 “[…] 因此，每一个不变量与协变式都可以用一个图来表示，而该图与 Kekulé 图或化学图完全相同。[…] 我给出了图的几何乘法规则，即如何根据给定的不变量或协变式的各自图，构造出它们乘积的图。[…]”（斜体为原文所示）

　　 图论的第一本教材由 Dénes Kőnig 编写，并于 1936 年出版。\(^\text{[26]}\) 另一部由 Frank Harary 于 1969 年出版的著作则被 “公认为该领域的权威教材”，\(^\text{[27]}\) 并使数学家、化学家、电气工程师和社会科学家能够彼此交流。Harary 将该书的全部版税捐出，用以资助 Pólya 奖。\(^\text{[28]}\)

　　 图论中最著名且最具启发性的问题之一是四色问题：“是否真的在平面上绘制的任何地图，都可以用四种颜色对其区域进行着色，使得任意两个有公共边界的区域颜色不同？” 这一问题最早由 Francis Guthrie 于 1852 年提出，其最早的书面记录出现在同年 De Morgan 写给 Hamilton 的一封信中。许多错误的证明曾被提出，包括 Cayley、Kempe 等人的工作。Tait、Heawood、Ramsey 和 Hadwiger 对该问题的研究及推广，推动了对嵌入在任意亏格曲面上的图的着色研究。Tait 的重新表述引出了新的问题类别——因子分解问题，其中由 Petersen 和 Kőnig 特别深入研究。Ramsey 在着色问题上的研究，尤其是 Turán 在 1941 年取得的结果，则催生了图论的另一分支：极值图论。

　　 四色问题在一个多世纪里一直未被解决。1969 年，Heinrich Heesch 发表了一种使用计算机解决该问题的方法。\(^\text{[29]}\)1976 年，Kenneth Appel 和 Wolfgang Haken 给出了一个计算机辅助证明，该证明根本性地利用了 Heesch 提出的 “放电法” 思想。\(^\text{[30][31]}\) 该证明需要通过计算机检验 1,936 种配置的性质，由于其复杂性，当时并未被完全接受。二十年后，Robertson、Seymour、Sanders 和 Thomas 提出了一个更为简洁的证明，仅需考虑 633 种配置。\(^\text{[32]}\)

　　 1860 至 1930 年间拓扑学的自主发展，通过 Jordan、Kuratowski 和 Whitney 的研究反过来滋养了图论。图论与拓扑学共同发展的另一重要因素来自现代代数方法的使用。其中的第一个例子是物理学家 Gustav Kirchhoff 的工作，他在 1845 年发表了基尔霍夫电路定律，用于计算电路中的电压和电流。

　　 概率方法在图论中的引入，尤其是 Erdős 和 Rényi 对图连通性的渐近概率研究，产生了另一分支：随机图论，这一领域不断产出丰硕的图论成果。

4. 表示

　　 图是自然界中关系的一种抽象，因此它本身并不固定于某种特定的表示方式。其表示方式取决于在具体应用中所提供的便利程度。最常见的表示方法有：可视化表示：通常将顶点绘制出来，并通过边连接；表格表示：通过表格的行来提供图中顶点之间关系的信息。

可视化：图的绘制

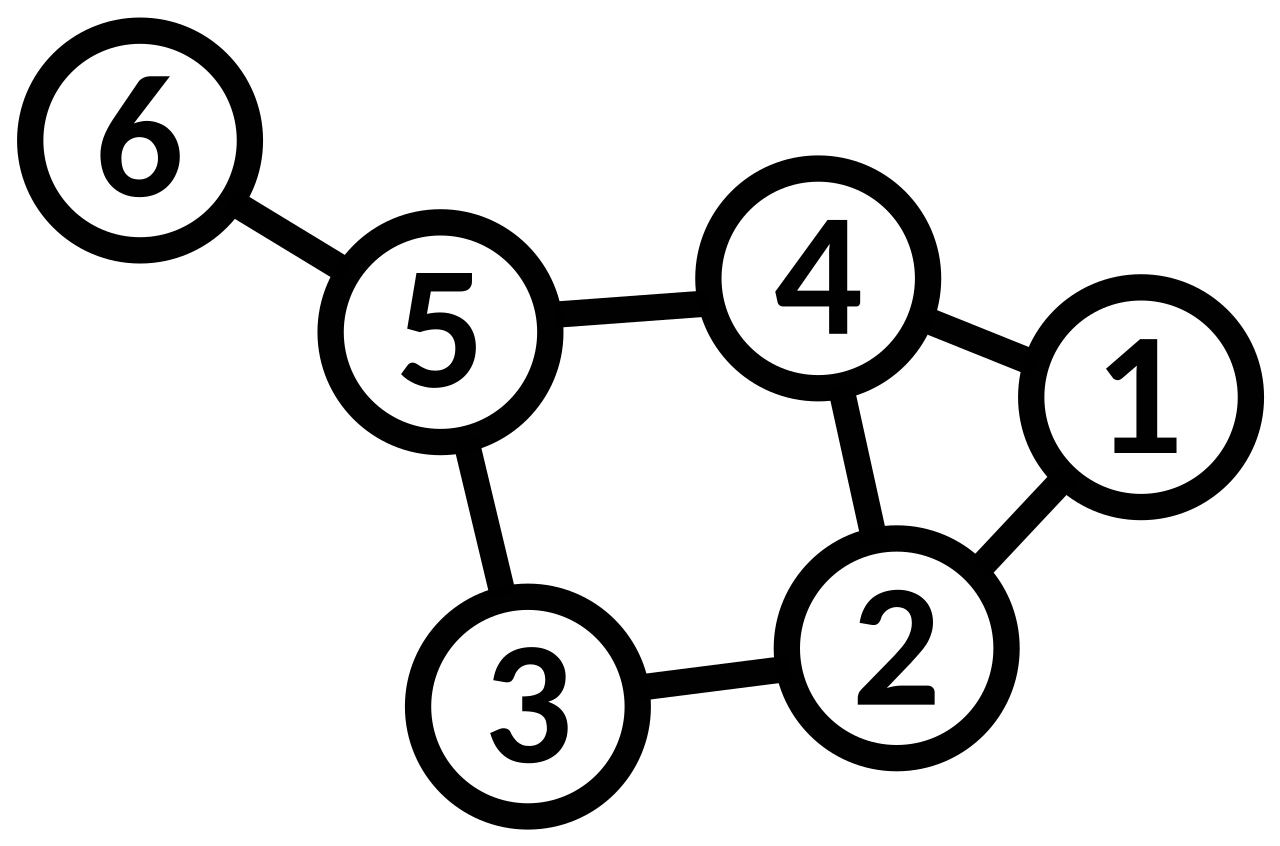
　　 图通常通过可视化来表示：为每个顶点绘制一个点或圆，如果两个顶点由一条边连接，则在它们之间画一条线。若图是有向的，则通过箭头表示方向；若图是加权的，则在箭头上标注权重。

　　 图的绘制不应与图本身（即抽象的、非可视化的结构）混淆，因为绘制图的方式有多种。真正重要的是哪些顶点彼此相连，以及通过多少条边相连，而不是绘图的具体布局。在实际操作中，往往很难判断两幅图的绘制是否表示同一个图。根据问题的不同领域，某些布局可能比其他布局更合适、更容易理解。

　　 W. T. Tutte 的开创性工作在图的绘制研究中具有极大影响。他的成就之一是引入了线性代数方法来获得图的绘制。

　　 图的绘制还涉及到交叉数及其各种推广。图的交叉数是指在平面上绘制该图时，边与边之间的最少交点数。对于平面图，交叉数按定义为零。此外，还研究在平面以外的其他曲面上绘制图的情形。

　　 除此之外，还有一些非传统的图可视化方法，不直接依赖顶点和边，例如圆填充、交叉图以及邻接矩阵的其他可视化方式。

表格表示：图的数据结构

　　 表格表示非常适合计算应用。在计算机系统中存储图的方法有多种。所使用的数据结构取决于图的结构以及操作图的算法。从理论上讲，可以区分为列表结构和矩阵结构，但在具体应用中，最优方案往往是两者结合。列表结构：适用于稀疏图，因为它们对内存的需求较小。矩阵结构：在某些应用中提供更快的访问速度，但可能消耗大量内存。当前的研究对象之一是在现代并行计算机架构上高效实现稀疏矩阵结构。\(^\text{[33]}\)

　　 边表：由顶点对组成的数组；邻接表：分别列出每个顶点的邻居顶点。与边表类似，但每个顶点都有一份与之邻接的顶点列表。

　　 矩阵结构包括：关联矩阵：由 0 和 1 组成的矩阵，行表示顶点，列表示边；邻接矩阵：行和列都由顶点索引，矩阵元素为 1 表示相邻，0 表示不相邻；度矩阵：表示各个顶点的度数；拉普拉斯矩阵：邻接矩阵的改进形式，结合了顶点度的信息，常用于某些计算，例如基尔霍夫关于图生成树数量的定理；距离矩阵：与邻接矩阵类似，行和列由顶点索引，但矩阵元素表示两个顶点之间最短路径的长度，而不是 0 或 1。

5. 问题

枚举

　　 关于图的枚举（即计算满足特定条件的图的数量）已有大量文献。其中一部分工作可见于 Harary 和 Palmer (1973)。

子图、诱导子图与图的子式

　　 一个常见的问题是子图同构问题：即在给定图中寻找一个固定图作为其子图。之所以关注这一问题，其中一个原因是许多图的性质对其子图是遗传性的，也就是说，一个图具有某种性质，当且仅当它的所有子图也具有该性质。寻找某类最大子图通常是一个 NP 完全问题。例如：

　　 子图同构的一个特殊情况是图同构问题。它询问两个图是否同构。目前尚不清楚该问题是否属于 NP 完全问题，也不清楚是否能在多项式时间内解决。

　　 一个类似的问题是在给定图中寻找诱导子图。同样，一些重要的图性质对于诱导子图来说是遗传的，也就是说，一个图具有某种性质，当且仅当它的所有诱导子图也具有该性质。寻找某类最大诱导子图通常也是 NP 完全问题。例如：

　　 还有一种类似的问题是图的子式包含问题，即在给定图中寻找一个固定图作为其子式。图的子式或收缩子图是通过取一个子图并收缩其中一些（或不收缩任何）边而得到的任意图。许多图的性质对其子式来说是遗传的，也就是说，一个图具有某种性质，当且仅当它的所有子式也具有该性质。例如，瓦格纳定理表明：

　　 一个类似的问题是细分包含问题，即在给定图中寻找一个固定图作为其细分。图的细分（或称为同胚图 homeomorphism）是通过将某些（或不进行任何）边细分而得到的任意图。细分包含与图的某些性质有关，例如平面性。例如，库拉托夫斯基定理表明：

图的着色

　　 图论中的许多问题与定理都涉及对图进行各种方式的着色。通常，我们关心的是对图进行着色，使得任意两个相邻顶点不具有相同的颜色，或者满足其他类似的限制条件。也可以考虑对边进行着色（例如要求任意两条相邻的边不具有相同颜色），或其他变体。

　　 与图着色相关的一些著名结果与猜想包括：

包含与统一

　　 约束建模理论涉及由偏序关系联系的一类有向图。在这些应用中，图按照特异性排序，即更受约束的图（更加具体，因此包含更多信息）被更一般的图包含。图之间的操作包括：判断两个图之间是否存在包含关系及其方向；计算图的统一。两个论证图的统一被定义为与输入一致（即包含所有输入信息）的最一般的图（或对其的计算），如果这样的图存在的话。目前已有高效的统一算法。

　　 对于严格可组合的约束框架而言，图统一就是充分的可满足性与组合函数。著名的应用包括自动定理证明以及语言结构展开的建模。

路径问题

网络流

　　 在应用中，有许多问题与网络中的各种流的概念相关，例如：

可见性问题

覆盖问题

　　 图中的覆盖问题可能涉及顶点或子图子集上的各种集合覆盖问题：

分解问题

　　 分解被定义为：将一个图的边集划分为若干部分（每部分伴随尽可能多的顶点，以包含这些边）。围绕这一概念有许多问题。常见的问题是：将一个图分解为与某个固定图同构的子图；例如，将一个完全图分解为若干条哈密顿回路。另一类问题则要求分解为某个特定图族，例如：分解为一族环，或将完全图 $K_n$ 分解为 $n-1$ 棵指定的树，这些树分别具有 $1,2,3,\ldots,n-1$ 条边。

　　 一些已被研究的具体分解问题及类似问题包括：

图的类别

　　 许多问题涉及对不同类别的图的成员进行刻画。此类问题的例子包括：

6. 参见

分支领域

7. 注释

  1. Bender & Williamson 2010，第 148 页。
  2. 参见，例如 Iyanaga 和 Kawada，69 J，第 234 页，或 Biggs，第 4 页。
  3. Bender & Williamson 2010，第 149 页。
  4. 参见，例如 Graham 等人，第 5 页。
  5. Bender & Williamson 2010，第 161 页。
  6. Hale, Scott A. (2014). Multilinguals and Wikipedia editing. 载于 Proceedings of the 2014 ACM conference on Web science，第 99–108 页。arXiv:1312.0976. Bibcode:2013arXiv1312.0976H. doi:10.1145/2615569.2615684. ISBN 978-1-4503-2622-3. S2CID 14027025.
  7. Mashaghi, A.; 等 (2004). Investigation of a protein complex network. European Physical Journal B. 41 (1): 113–121. arXiv:cond-mat/0304207. Bibcode:2004EPJB...41..113M. doi:10.1140/epjb/e2004-00301-0. S2CID 9233932.
  8. Shah, Preya; Ashourvan, Arian; Mikhail, Fadi; Pines, Adam; Kini, Lohith; Oechsel, Kelly; Das, Sandhitsu R; Stein, Joel M; Shinohara, Russell T (2019-07-01). Characterizing the role of the structural connectome in seizure dynamics. Brain. 142 (7): 1955–1972. doi:10.1093/brain/awz125. ISSN 0006-8950. PMC 6598625. PMID 31099821.
  9. Adali, Tulay; Ortega, Antonio (2018 年 5 月). Applications of Graph Theory [Scanning the Issue]. Proceedings of the IEEE. 106 (5): 784–786. doi:10.1109/JPROC.2018.2820300. ISSN 0018-9219.
  10. Grandjean, Martin (2016). A social network analysis of Twitter: Mapping the digital humanities community (PDF). Cogent Arts & Humanities. 3 (1) 1171458. doi:10.1080/23311983.2016.1171458. S2CID 114999767.
  11. Vecchio, F (2017). “阿尔茨海默病中大脑连接的小世界结构与海马体积：基于 EEG 数据的图论研究”。Brain Imaging and Behavior. 11 (2): 473–485. doi:10.1007/s11682-016-9528-3. PMID 26960946. S2CID 3987492.
  12. Vecchio, F (2013). “额颞叶痴呆中基于图论的大脑网络连接性评估”*。Neurology. 81 (2): 134–143. doi:10.1212/WNL.0b013e31829a33f8. PMID 23719145. S2CID 28334693.
  13. Bjorken, J. D.; Drell, S. D. (1965). Relativistic Quantum Fields. New York: McGraw-Hill. p. viii.
  14. Kumar, Ankush; Kulkarni, G. U. (2016-01-04). “从几何学角度评估基于导电网络的透明电极”。Journal of Applied Physics. 119 (1): 015102. Bibcode:2016JAP...119a5102K. doi:10.1063/1.4939280. ISSN 0021-8979.
  15. Newman, Mark (2010). Networks: An Introduction (PDF). Oxford University Press. 原始 (PDF) 存档于 2020-07-28. 检索于 2019-10-30.
  16. Grandjean, Martin (2015). “社会网络分析与可视化：重访 Moreno 的社会图”。改造后的网络严格基于 Moreno (1934) Who Shall Survive.
  17. Rosen, Kenneth H. (2011-06-14). 离散数学及其应用（第 7 版）。New York: McGraw-Hill. ISBN 978-0-07-338309-5.
  18. Kelly, S.; Black, Michael (2020-07-09). “graphsim: 一个用于从生物通路图结构中模拟基因表达数据的 R 包” (PDF)。Journal of Open Source Software. 5 (51). The Open Journal: 2161. Bibcode:2020JOSS....5.2161K. bioRxiv 10.1101/2020.03.02.972471. doi:10.21105/joss.02161. ISSN 2475-9066. S2CID 214722561.
  19. Shah, Preya; Ashourvan, Arian; Mikhail, Fadi; Pines, Adam; Kini, Lohith; Oechsel, Kelly; Das, Sandhitsu R; Stein, Joel M; Shinohara, Russell T (2019-07-01). “癫痫动态中结构连接组的作用特征化”*。Brain. 142 (7): 1955–1972. doi:10.1093/brain/awz125. ISSN 0006-8950. PMC 6598625. PMID 31099821.
  20. Biggs, N.; Lloyd, E.; Wilson, R. (1986). Graph Theory, 1736–1936. Oxford University Press.
  21. Cauchy, A. L. (1813). “关于多面体的研究——第一篇论文”。Journal de l'École Polytechnique 9 (Cahier 16): 66–86.
  22. L'Huillier, S.-A.-J. (1812–1813). “关于多面体测量的论文”。Annales de Mathématiques. 3: 169–189.
  23. Cayley, A. (1857). “关于被称为树的解析形式的理论”。Philosophical Magazine, Series IV, 13 (85): 172–176. doi:10.1017/CBO9780511703690.046. ISBN 978-0-511-70369-0.
  24. Cayley, A. (1875). “论数学中被称为树的解析图形及其在化学化合物理论中的应用”。Berichte der Deutschen Chemischen Gesellschaft. 8 (2): 1056–1059. doi:10.1002/cber.18750080252.
  25. Sylvester, James Joseph (1878). “化学与代数”。Nature. 17 (432): 284. Bibcode:1878Natur..17..284S. doi:10.1038/017284a0.
  26. Tutte, W. T. (2001). Graph Theory Cambridge University Press, p. 30. ISBN 978-0-521-79489-3. 检索于 2016-03-14.
  27. Gardner, Martin (1992). Fractal Music, Hypercards, and more…Mathematical Recreations from Scientific American. W. H. Freeman and Company, p. 203.
  28. Society for Industrial and Applied Mathematics (2002). “George Pólya 奖”，载于 Looking Back, Looking Ahead: A SIAM History (PDF), p. 26. 原始 (PDF) 存档于 2016-03-05. 检索于 2016-03-14.
  29. Heinrich Heesch (1969). Untersuchungen zum Vierfarbenproblem. Mannheim: Bibliographisches Institut.
  30. Appel, K.; Haken, W. (1977). “每个平面图都是四色可着色的. 第一部分：放电法”(PDF)。Illinois J. Math. 21 (3): 429–490. doi:10.1215/ijm/1256049011.
  31. Appel, K.; Haken, W. (1977). “每个平面图都是四色可着色的. 第二部分：可约性”。Illinois J. Math. 21 (3): 491–567. doi:10.1215/ijm/1256049012.
  32. Robertson, N.; Sanders, D.; Seymour, P.; Thomas, R. (1997). “四色定理”。Journal of Combinatorial Theory, Series B. 70: 2–44. doi:10.1006/jctb.1997.1750.
  33. Kepner, Jeremy; Gilbert, John (2011). Graph Algorithms in the Language of Linear Algebra. SIAM, p. 1171458. ISBN 978-0-898719-90-1.

8. 参考文献

9. 外部链接

在线教材

                     

© 保留一切权利