拓扑空间（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　 在数学中，拓扑空间可以粗略地理解为一种定义了 “接近性” 但不一定能用数值距离来度量的几何空间。更具体地说，拓扑空间是一个集合，其元素称为点，并配备一种称为拓扑的附加结构。这个拓扑可以定义为：每个点都对应一组满足特定公理的邻域集合，这些公理用来形式化 “接近性” 的概念。拓扑有多种等价的定义方式，其中最常用的是通过开集来定义。

　　 拓扑空间是最一般的数学空间形式，能够支持极限、连续性以及连通性等概念的定义 \(^\text{[1][2]}\)。常见的拓扑空间类型包括欧几里得空间、度量空间以及流形。

　　 尽管拓扑空间的概念非常抽象和宽泛，但它是数学中的一个基础性概念，几乎存在于现代数学的各个分支中。专门研究拓扑空间本身的学科被称为一般拓扑学，也叫点集拓扑学。

1. 历史

　　 大约在 1735 年，莱昂哈德·欧拉发现了公式：$V - E + F = 2$ 其中 $V$ 表示顶点数，$E$ 表示边数，$F$ 表示面数，该公式刻画了凸多面体（以及平面图）的数量关系。这一公式的研究与推广，尤其是由柯西（Augustin-Louis Cauchy, 1789–1857）和吕利耶（Simon Antoine Jean L'Huilier, 1750–1840）的深入研究，极大地推动了拓扑学的发展。在 1827 年，卡尔·弗里德里希·高斯发表了《曲面的一般研究》。在第三节中，他以类似现代拓扑的方式定义了曲面：“如果从曲面上一点 A 向与 A 无穷接近的曲面点引出的所有直线的方向，相对于通过 A 的同一平面发生无穷小的偏转，那么该曲面在 A 点就被称为具有连续曲率。\(^\text{[3]}\)”

　　 然而，“直到黎曼在 19 世纪 50 年代初的工作之前，曲面一直是从局部角度（作为参数曲面）来研究的，拓扑问题从未被考虑过。” 莫比乌斯和乔尔当似乎是最早意识到拓扑学的核心问题是寻找不变量（最好是数值不变量），以此来判断两个曲面是否等价，即判断它们是否同胚。\(^\text{[4]}\)

　　 费利克斯·克莱因在其 “埃尔兰根纲领”（Erlangen Program, 1872 中明确提出：研究任意连续变换下的不变量是一种新的几何学，即拓扑学的雏形。“拓扑学” 一词由约翰·本尼迪克特·李斯廷于 1847 年首次提出，尽管他在几年前的通信中已经使用过该术语来代替当时常用的 “位置分析”。昂利·庞加莱将这一学科扩展到任意维度的空间，并奠定了现代拓扑学的基础。他关于该主题的第一篇论文发表于 1894 年。\(^\text{[5]}\) 在 1930 年代，詹姆斯·沃德尔·亚历山大二世和哈斯勒·惠特尼首次提出了这样的观点：曲面是一种局部类似欧几里得平面的拓扑空间。

　　 拓扑空间的现代定义最早由费利克斯·豪斯多夫于 1914 年在其奠基性著作 《集合论的原理》中提出。度量空间则更早在 1906 年由莫里斯·弗雷歇定义，但 “度量空间”（德语：metrischer Raum）这一术语的普及归功于豪斯多夫 \(^\text{[6][7]}\)。

2. 定义

　　 拓扑这一概念的实用性在于：这种数学结构有多种等价的定义，可以根据具体应用选择最合适的公理化形式。最常用的定义是基于开集的方式，但基于邻域的定义可能更直观，因此通常先给出这一形式。

基于邻域的定义

　　 这种公理化方法最早由费利克斯·豪斯多夫提出。设 $X$ 是一个（可能为空的）集合，$X$ 的元素通常称为点，但实际上它们可以是任何数学对象。令 $\mathcal{N}$ 是一个函数，为 $X$ 中的每个点 $x$ 赋予一个非空的子集族 $\mathcal{N}(x)$，这些子集都属于 $X$ 的子集。$\mathcal{N}(x)$ 中的元素称为点 $x$ 的邻域（neighbourhoods of $x$，或简称邻域）。如果以下公理成立，那么函数 $\mathcal{N}$ 被称为一个邻域拓扑，此时 $X$ 与 $\mathcal{N}$ 构成一个拓扑空间。

　　 公理

  1. 点属于其每个邻域,若 $N$ 是 $x$ 的一个邻域（即 $N \in \mathcal{N}(x)$），则：$x \in N$ 换句话说，集合 $X$ 中的每个点都属于它的每一个邻域。
  2. 邻域的超集仍是邻域,若 $N \subseteq X$，且 $N$ 包含了 $x$ 的某个邻域，则：$N \in \mathcal{N}(x)$ 也就是说，点 $x$ 的邻域的任意超集仍然是 $x$ 的邻域。
  3. 邻域的交集仍是邻域,若 $N_1, N_2 \in \mathcal{N}(x)$，则：$N_1 \cap N_2 \in \mathcal{N}(x)$
  4. 局部一致性,对于点 $x$ 的任意邻域 $N$，总存在另一个邻域 $M \subseteq N$ 使得：$\forall y \in M, \; N \in \mathcal{N}(y)$ 换句话说，点 $x$ 的任意邻域中都包含一个更小的邻域，这个更小的邻域中的每个点也都 “共享” 原来的邻域。

　　 邻域的前三条公理有着直观的含义，而第四条公理在理论结构中具有非常重要的作用，它用于将空间 $X$ 中不同点的邻域联系起来。

　　 一个标准的邻域系统示例是实数轴 $\mathbb{R}$：当 $\mathbb{R}$ 的一个子集 $N$ 包含某个实数 $x$ 附近的一个开区间时，就称 $N$ 是 $x$ 的一个邻域。

　　 在这种结构下，如果集合 $U \subseteq X$ 对于其中的每个点都是该点的邻域，则称集合 $U$ 是开集。这些开集满足下一个拓扑空间定义中的开集公理。反过来，当我们已知一个拓扑空间的开集后，也可以重新得到满足上述邻域公理的邻域系统：如果集合 $N$ 包含一个开集 $U$ 且 $x \in U$，则称 $N$ 是点 $x$ 的邻域 \(^\text{[9]}\)。

通过开集定义

　　 一个集合 $X$ 上的拓扑可以定义为一个子集族 $\tau$，称为开集，并且满足以下公理 \(^\text{[10]}\)：

  1. 空集与全集.空集 $\varnothing$ 和全集 $X$ 都属于 $\tau$。
  2. 任意并集封闭.$\tau$ 中任意子集族（无论有限或无限）的并集仍然属于 $\tau$。
  3. 有限交集封闭.$\tau$ 中任意有限多个子集的交集仍然属于 $\tau$。

　　 由于这种定义是最常用的，因此集合 $\tau$ 也通常被称为集合 $X$ 上的拓扑。

　　 一个子集 $C \subseteq X$ 称为在 $(X, \tau)$ 中闭集，当且仅当它的补集 $X \setminus C$ 是开集。由此可以推出：空集 $\varnothing$ 和全集 $X$ 既是开集又是闭集，因为它们互为补集，并且每个本身都是开集。一般地，任何在 $X$ 中同时是开集又是闭集的子集，称为闭开集。

　　 拓扑的示例

图
图 1：令 $\tau$ 用圆圈表示，下面展示了在三元素集合 $\{1, 2, 3\}$ 上的四个拓扑示例和两个非拓扑示例。左下角的示例不是拓扑，因为集合 $\{2\}$ 与 $\{3\}$ 的并集（即 $\{2, 3\}$）缺失。右下角的示例也不是拓扑，因为集合 $\{1, 2\}$ 与 $\{2, 3\}$ 的交集（即 $\{2\}$）缺失。
  1. 设 $X = \{1, 2, 3, 4\}$：平凡拓扑 / 不分化拓扑.族 $\tau = \{\{\}, \{1, 2, 3, 4\}\} = \{\varnothing, X\}$ 仅包含拓扑公理要求的两个子集，即空集与全集，这样的 $\tau$ 构成了 $X$ 上的一个拓扑。
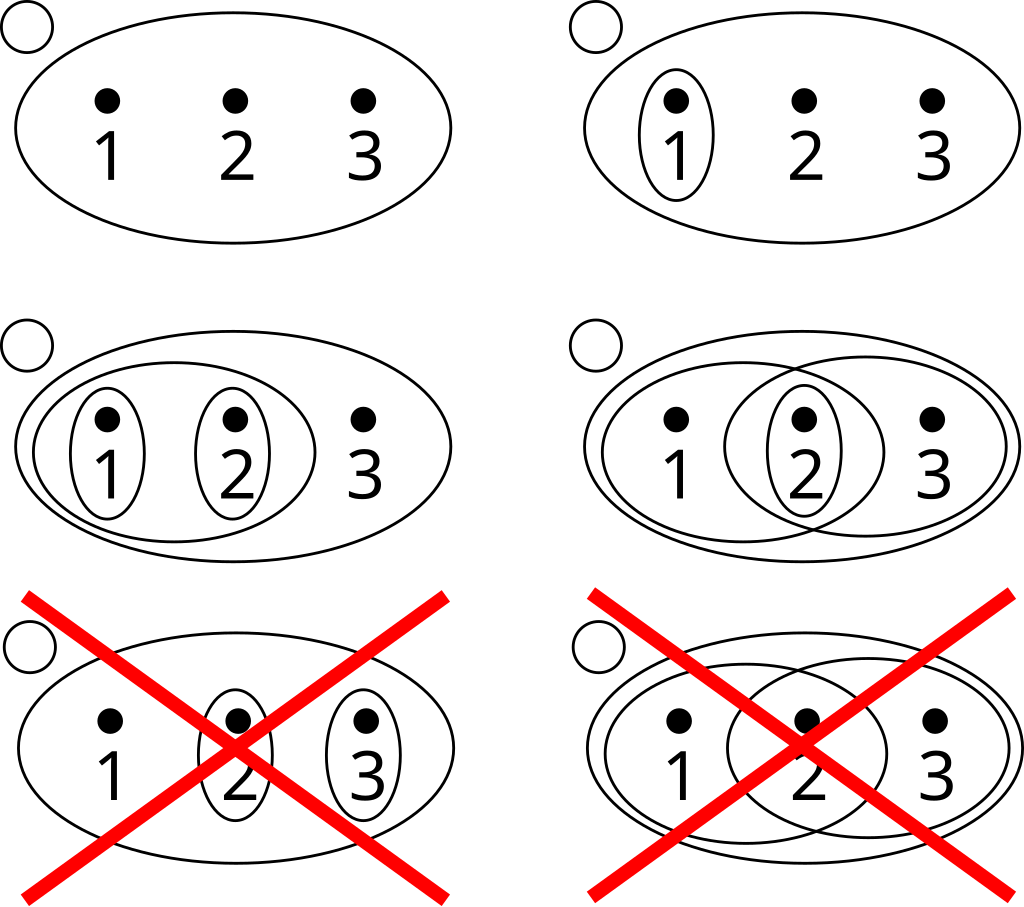
  2. 另一种拓扑.族 $\tau = \{\varnothing, \{2\}, \{1, 2\}, \{2, 3\}, \{1, 2, 3\}, X\}$ 包含 6 个子集，这同样构成了 $X$ 上的另一个拓扑。
  3. 离散拓扑.若取 $X$ 的幂集 $\tau = \wp(X)$ 即所有可能的子集，则得到的是离散拓扑，此时的拓扑空间 $(X, \tau)$ 被称为离散空间。
  4. 一个非拓扑的例子.设 $X = \mathbb{Z}$（整数集），令 $\tau$ 为 “所有整数的有限子集，加上 $\mathbb{Z}$ 本身”。这个集合族不是一个拓扑，因为例如 “所有不包含 0 的有限子集的并集” 不是有限集，因此不在该集合族中；而这个并集也不是 $\mathbb{Z}$ 本身，所以它也不满足拓扑公理要求。

3. 通过闭集定义

　　 利用德摩根律，前面对开集的公理可以转化为闭集的等价公理：

  1. 空集 $\varnothing$ 和全集 $X$ 都是闭集。
  2. 任意族闭集的交集仍然是闭集。
  3. 有限多个闭集的并集仍然是闭集。

　　 根据这些公理，可以从另一个角度定义拓扑空间：拓扑空间是一个集合 $X$，以及一个闭子集族 $\tau$。此时，$\tau$ 中的集合就是闭集，而它们在 $X$ 中的补集就是开集。

其他定义

　　 拓扑空间还有许多等价的定义方式。换句话说，邻域、开集或闭集的概念都可以从其他出发点重新构造，并满足相应的公理。

　　 另一种定义拓扑空间的方法是利用 Kuratowski 闭包公理，它将闭集定义为集合 $X$ 幂集上的一个算子的不动点。

　　 此外，网的概念是序列的推广。若对集合 $X$ 中的每一个网，其所有聚点都被指定出来，那么该拓扑也就被完全确定了。

4. 拓扑的比较

　　 在一个集合上可以定义许多不同的拓扑，从而形成不同的拓扑空间。当一个拓扑 $\tau_1$ 的每一个开集在另一个拓扑 $\tau_2$ 中也都是开集时，就称 $\tau_2$ 比 $\tau_1$ 更细，相应地，$\tau_1$ 比 $\tau_2$ 更粗。如果一个证明仅依赖于某些集合是开集，那么它对任何更细的拓扑都成立；同样地，如果一个证明依赖于某些集合不是开集，那么它对任何更粗的拓扑也都适用。有时，人们用 “更大” 和 “更小” 来替代 “更细” 和 “更粗”。也有文献中使用 “更强” 和 “更弱” 这样的术语，但其具体含义并不统一，因此阅读时需要特别注意作者的约定。

　　 在一个给定集合 $X$ 上，所有可能的拓扑的集合构成一个完备格：若 $F = \{\tau_\alpha : \alpha \in A\}$ 是 $X$ 上的一族拓扑，则：交是 $F$ 中所有拓扑的交集；并是所有包含 $F$ 中每个拓扑的拓扑的交集。

5. 连续函数

　　 设 $f: X \to Y$ 是两个拓扑空间之间的一个函数，如果对于每个 $x \in X$ 以及 $f(x)$ 的每一个邻域 $N$，都存在 $x$ 的一个邻域 $M$，使得：$f(M) \subseteq N$,那么 $f$ 称为连续函数。这个定义与分析学中常见的连续性概念密切相关。等价地，函数 $f$ 连续当且仅当每个开集的逆像仍然是开集 \(^\text{[11]}\)。这样的定义试图刻画函数 “没有跳跃或断裂” 的直观概念。一个同胚是指一个双射函数，它本身连续且其逆函数也是连续的。如果两个空间之间存在同胚映射，则称这两个空间是同胚的。从拓扑学的角度来看，同胚空间本质上是完全相同的 \(^\text{[12]}\)。

　　 在范畴论中，一个基本的范畴是 Top，表示拓扑空间的范畴，其中对象是拓扑空间，态射是连续函数。尝试通过不变量对该范畴的对象进行分类，推动了多个研究领域的发展，例如同伦理论、同调理论以及 K-理论。

6. 拓扑空间的示例

　　 一个给定的集合可以定义出许多不同的拓扑。若一个集合被赋予不同的拓扑，它就被视为不同的拓扑空间。离散拓扑,任何集合都可以赋予离散拓扑，即每个子集都是开集。在这种拓扑中，序列或网只有在 “最终保持常值” 时才收敛。平凡拓扑 / 不分化拓扑,任何集合也可以赋予平凡拓扑，即只有空集与全集是开集。在这种拓扑中，每个序列或网都会收敛到空间中的每一个点。这一示例表明，在一般的拓扑空间中，序列的极限并不一定是唯一的。不过，在 Hausdorff 空间中，极限点是唯一的。

　　 有限拓扑空间,在任意有限集合上，可以定义出许多不同的拓扑，这些空间称为有限拓扑空间。有限空间常用于提供拓扑猜想的示例或反例。

　　 余有限拓扑,任何集合都可以赋予余有限拓扑，即开集只有空集和补集为有限集的子集。在任意无限集合上，余有限拓扑是最小的 $T_1$ 拓扑 \(^\text{[13]}\)。

　　 余可数拓扑,在这种拓扑中，一个集合是开集，当且仅当它是空集或其补集是可数集。当底层集合是不可数集时，这种拓扑常作为许多情境下的反例。

　　 下限拓扑,在实数轴 $\mathbb{R}$ 上，可以定义下限拓扑，其基本开集是半开区间 $[a, b)$。这种拓扑比标准欧几里得拓扑更细。在这种拓扑下，一个序列收敛到某点，当且仅当它在欧几里得拓扑下是 “从上方” 收敛的。这个例子表明，在同一个集合上可以定义出许多彼此不同的拓扑。

　　 序数拓扑,若 $\gamma$ 是一个序数，则集合 $\gamma = [0, \gamma)$ 可以赋予序拓扑，其基由区间 $(\alpha, \beta)$、$[0, \beta)$ 和 $(\alpha, \gamma)$ 生成，其中 $\alpha, \beta \in \gamma$。

　　 流形与单形的自然拓扑,每个流形都有一个自然拓扑，因为它局部是欧几里得空间。同样地，每个单形和单纯复形也自然继承了拓扑。

　　 谢尔宾斯基空间,是最简单的非离散拓扑空间，它在计算理论和语义学中有重要应用。

由其他拓扑导出的拓扑

　　 拓扑空间的每个子集都可以赋予子空间拓扑：其开集是由 “大空间” 的开集与该子集的交集所形成的集合。对于任意按索引排列的一族拓扑空间，可以通过积拓扑来构造它们的笛卡尔积空间： 该拓扑由投影映射下各因子空间开集的原像生成。在有限积中，积拓扑的一个基由所有因子空间开集的乘积组成。在无限积中，还需满足额外条件：在一个基本开集中，除有限多个投影外，其余投影必须是整个空间。这种构造是初始拓扑的一个特例。

　　 商空间定义如下：若 $X$ 是一个拓扑空间，$Y$ 是一个集合，且 $f: X \to Y$ 是一个满射函数，则 $Y$ 上的商拓扑定义为：所有在 $f$ 下的逆像是 $X$ 中开集的子集的集合。换句话说，商拓扑是使 $f$ 连续的最细拓扑。一个常见的例子是：当 $X$ 上定义了一个等价关系时，映射 $f$ 是从 $X$ 到等价类集合的自然投影。这种构造是终拓扑的一个特例。

度量空间

　　 度量空间体现了一种度量，即对空间中两点之间 “距离” 的精确定义。

　　 每一个度量空间都可以赋予度量拓扑：其基本开集由该度量定义的开球组成。这种拓扑就是赋范向量空间的标准拓扑。在有限维向量空间中，无论采用哪种范数，所生成的拓扑都是相同的。

　　 在实数集 $\mathbb{R}$ 上有多种方式可以定义拓扑。标准拓扑由开区间生成：所有开区间的集合形成了该拓扑的一个基，意味着任意开集都是某些基元素的并集。换句话说，一个集合是开集，当且仅当它的每个点都有一个半径大于 0 的开区间包含在该集合中。更一般地，欧几里得空间 $\mathbb{R}^n$ 也可以赋予拓扑，在标准拓扑中，其基本开集是开球。同样地，复数集 $\mathbb{C}$ 以及 $\mathbb{C}^n$ 也有标准拓扑，其基本开集同样是开球。

由代数结构导出的拓扑

　　 对于任意代数对象，都可以赋予离散拓扑，此时所有代数运算都是连续函数。对于那些无限的代数结构，往往可以定义一种自然拓扑，使得代数运算依然保持连续性。这就引出了诸如拓扑群、拓扑环、拓扑域以及基于这些拓扑域的拓扑向量空间等概念。在数论中，局部域就是一种重要的拓扑域。

　　 Zariski 拓扑通过代数方法定义在环的谱或代数簇上。在 $\mathbb{R}^n$ 或 $\mathbb{C}^n$ 中，Zariski 拓扑的闭集是多项式方程组的解集。

具有序结构的拓扑空间

由其他结构导出的拓扑

　　 若 $\Gamma$ 是集合 $X$ 上的一个滤子，则 $\{\varnothing\} \cup \Gamma$ 构成 $X$ 上的一个拓扑。

　　 在泛函分析中，许多线性算子集都会赋予一种特殊的拓扑，这些拓扑通过指定某类函数序列何时收敛到零函数来定义。

　　 线性图具有一种自然的拓扑，它推广了带有顶点和边的图的许多几何性质。

　　 自由群 $F_n$ 的外空间由该自由群上体积为 1 的所谓 “标记度量图结构” 组成 \(^\text{[14]}\)。

7. 拓扑空间的分类

　　 拓扑空间可以依据它们的拓扑性质（即在同胚下保持不变的性质）进行广义分类。若两个空间是同胚的，它们必然拥有相同的拓扑性质。因此，要证明两个空间不是同胚的，只需找到一个它们不共享的拓扑性质即可。常见的拓扑性质示例包括：连通性,紧致性,各种分离公理至于与代数相关的不变量，则可参考代数拓扑中的研究。

8. 参见

9. 引文

  1. Schubert 1968, p. 13
  2. Sutherland, W. A. (1975). *Introduction to metric and topological spaces*. Oxford [England]: Clarendon Press. ISBN 0-19-853155-9. OCLC 1679102.
  3. Gauss 1827.
  4. Gallier & Xu 2013.
  5. J. Stillwell, Mathematics and its history.
  6. “metric space”. Oxford English Dictionary (Online ed.). Oxford University Press.（需要订阅或参与机构访问权限）
  7. Hausdorff, Felix (1914) [1914]. “Punktmengen in allgemeinen Räumen”. Grundzüge der Mengenlehre. Göschens Lehrbücherei/Gruppe I: Reine und Angewandte Mathematik Serie (德文). Leipzig: Von Veit (2011 再版). p. 211. ISBN 9783110989854. 2022 年 8 月 20 日检索。原文：“Unter einem m e t r i s c h e n R a u m e verstehen wir eine Menge E, [...]”。
  8. Brown 2006, section 2.1.
  9. Brown 2006, section 2.2.
  10. Armstrong 1983, definition 2.1.
  11. Armstrong 1983, theorem 2.6.
  12. Munkres, James R (2015). Topology. Pearson. pp. 317–319. ISBN 978-93-325-4953-1.
  13. Anderson, B. A.; Stewart, D. G. (1969). “$T_1$-complements of $T_1$ topologies”. Proceedings of the American Mathematical Society. 23: 77–81. doi:10.2307/2037491. JSTOR 2037491. MR 0244927.
  14. Culler, Marc; Vogtmann, Karen (1986). “Moduli of graphs and automorphisms of free groups” (PDF). Inventiones Mathematicae. 84 (1): 91–119. Bibcode:1986InMat..84...91C. doi:10.1007/BF01388734. S2CID 122869546.

10. 参考书目

11. 外部链接

                     

© 保留一切权利