勒文海姆–斯科伦定理（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在数理逻辑中，洛文海姆–斯科伦定理（Löwenheim–Skolem theorem）是关于模型的存在性与基数的一个定理，以数学家莱奥波德·洛文海姆（Leopold Löwenheim）和托拉夫·斯科伦（Thoralf Skolem）的名字命名。

　　 其精确定义如下：若一个可数的一阶理论（countable first-order theory）存在一个无限模型，那么对于任意无限基数 \(\kappa\)，该理论都存在一个基数为 \(\kappa\) 的模型。这意味着，任何具有无限模型的一阶理论都不可能在同构意义下拥有唯一模型。

　　 由此可知，一阶理论无法控制其无限模型的基数。（向下的）洛文海姆–斯科伦定理是刻画一阶逻辑的两个关键性质之一，另一个是紧致性定理（compactness theorem）。这两者共同构成了林德斯特伦定理（Lindström’s theorem）的基础。而在更强的逻辑体系中（例如二阶逻辑），一般而言洛文海姆–斯科伦定理并不成立。\(^\text{[1]}\)

1. 定理

　　 在其最一般的形式下，洛文海姆–斯科伦定理（Löwenheim–Skolem Theorem）表述如下：

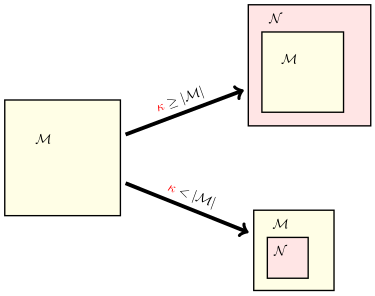
　　 对于任意签名（signature）\(\sigma\)，任意无限的 \(\sigma\)-结构 \(M\)，以及任意满足 \(\kappa \geq |\sigma|\) 的无限基数 \(\kappa\)，存在一个 \(\sigma\)-结构 \(N\)，使得 \(|N| = \kappa\)，并且：

• 若 \(\kappa < |M|\)，则 \(N\) 是 \(M\) 的一个初等子结构（elementary substructure）；
• 若 \(\kappa \geq |M|\)，则 \(N\) 是 \(M\) 的一个初等扩张（elementary extension）。

　　 该定理通常被分为上述两种情况： 第一部分（关于较小基数的初等子结构）称为向下洛文海姆–斯科伦定理（Downward Löwenheim–Skolem Theorem）\(^\text{[2]:160–162}\)；第二部分（关于较大基数的初等扩张）称为向上洛文海姆–斯科伦定理（Upward Löwenheim–Skolem Theorem）\(^\text{[3]}\)。

2. 讨论

　　 以下将进一步阐述签名（signature）与结构（structure）的基本概念。

概念

　　 签名

　　 一个签名由以下部分组成：一组函数符号 \(S_{\text{func}}\)，一组关系符号 \(S_{\text{rel}}\)，以及一个函数 \(\operatorname{ar} : S_{\text{func}} \cup S_{\text{rel}} \to \mathbb{N}_0\) 表示各符号的元数（arity）。一个元数为 0 的函数符号称为常数符号。在一阶逻辑中，签名有时也被称为语言（language）。若其函数符号与关系符号的集合是可数的，则称该签名为可数签名。一般而言，签名的基数就是它所包含全部符号集合的基数。

　　 一个一阶理论（first-order theory）由固定的签名与该签名下的一组句子（无自由变元的公式）组成 \(^\text{[4]:40}\)。理论常常通过：给出一组公理以生成该理论，或指定一个结构并令该理论由该结构满足的所有句子组成， 来定义。

　　 结构 / 模型

　　 给定一个签名 \(\sigma\)，一个 \(\sigma\)-结构 \(M\) 是对 \(\sigma\) 中符号的具体解释。它包括一个基础集合（通常也记为 \(M\)），以及对函数符号和关系符号的解释。一个常数符号在 \(M\) 中的解释就是 \(M\) 的某个元素；一个 \(n\)-元函数符号 \(f\) 的解释是一个映射 \(f^M : M^n \to M\)；一个关系符号 \(R\) 的解释是 \(M\) 上的一个 \(n\)-元关系，即 \(M^n\) 的一个子集。

　　 一个 \(\sigma\)-结构 \(M\) 的子结构（substructure）是这样获得的： 取 \(M\) 的一个子集 \(N\)，使其对所有函数符号的解释封闭（因此包含所有常数符号的解释），并将关系符号的解释限制到 \(N\)。初等子结构（elementary substructure）是子结构中特殊的一种，它与原结构（其初等扩张）满足完全相同的一阶句子。

推论

　　 在引言中给出的结论可直接由取 \( M \) 为该理论的任意无限模型而得。 该定理的 “向上” 部分的证明还表明：若一个理论具有任意大的有限模型，则它必然也有一个无限模型；有时这一结果也被视为定理的一部分。\(^\text{[2]}\)

　　 一个理论若仅有一个模型（模同构而言），则称其为范畴的（categorical）。该术语最早由 Veblen（1904）提出。在随后的若干年间，数学家曾希望能够通过描述某种版本的集合论的一阶范畴理论，从而为整个数学建立一个坚实的逻辑基础。然而，洛文海姆–斯科伦定理给这一希望第一次致命打击：它表明，一个拥有无限模型的一阶理论不可能是范畴的。随后在 1931 年，哥德尔不完备定理（Gödel’s incompleteness theorem）彻底摧毁了这一希望。\(^\text{[2]}\)

　　 在 20 世纪早期，洛文海姆–斯科伦定理的许多推论在逻辑学家看来颇为违反直觉，因为当时人们尚未充分理解 “一阶性质” 与 “非一阶性质” 的区别。其中一个重要的推论是：存在不可数模型的 “真算术”（true arithmetic），这些模型满足所有一阶归纳公理，但却含有非归纳子集。

　　 设 \(\mathbb{N}\) 表示自然数集，\(\mathbb{R}\) 表示实数集。根据该定理可知： 理论 \((\mathbb{N}, +, \times, 0, 1)\)（即真的一阶算术理论）存在不可数模型；理论 \((\mathbb{R}, +, \times, 0, 1)\)（即实闭域理论）存在可数模型。当然，存在一些公理化系统能刻画 \((\mathbb{N}, +, \times, 0, 1)\) 与 \((\mathbb{R}, +, \times, 0, 1)\) 到同构为止，但洛文海姆–斯科伦定理说明：这些公理化系统不可能是一阶的。例如，在实数理论中，用于刻画 \(\mathbb{R}\) 为 “完备有序域” 的线性序的完备性性质，便是一个非一阶性质。\(^\text{[2]:161}\)

　　 另一个被认为尤其令人不安的推论是：存在一个可数的集合论模型，但该模型仍然满足 “实数集是不可数的” 这一命题。康托尔定理（Cantor’s theorem）指出某些集合是不可数的，而这一现象产生的悖论性局面被称为斯科伦悖论（Skolem’s paradox）。它揭示了一个深刻的事实：“可数性” 这一概念并非绝对，而是相对模型而定的。\(^\text{[5]}\)

3. 证明概述

向下部分

　　 对于每一个一阶 \(\sigma\)-公式 \(\varphi(y, x_1, \ldots, x_n)\),选择公理（Axiom of Choice）蕴含存在一个函数 \[ f_\varphi : M^n \to M~ \] 使得对所有 \(a_1, \ldots, a_n \in M\)，要么： \[ M \models \varphi(f_\varphi(a_1, \ldots, a_n), a_1, \ldots, a_n)~ \] 要么： \[ M \models \neg \exists y \, \varphi(y, a_1, \ldots, a_n)~ \] 再次应用选择公理，我们可以得到一个从所有一阶公式 \(\varphi\) 到这些函数 \(f_\varphi\) 的映射。

　　 这一族函数 \(f_\varphi\) 诱导出一个作用于 \(M\) 的幂集上的预闭包算子（preclosure operator）： \[ F(A) = \{\, f_\varphi(a_1, \ldots, a_n) \in M \mid \varphi \in \sigma, \; a_1, \ldots, a_n \in A \,\}, \quad A \subseteq M~ \] 对 \(F\) 进行可数次迭代得到一个闭包算子 \(F^\omega\)。取任意子集 \(A \subseteq M\)，满足 \(|A| = \kappa\)，定义 \(N = F^\omega(A)\)。可以证明 \(|N| = \kappa\)。根据 Tarski–Vaught 判别法，此时 \(N\) 是 \(M\) 的一个初等子结构。

　　 此证明中使用的技巧最早可追溯到 斯科伦（Skolem），他在语言中引入了表示这些斯科伦函数 \(f_\varphi\) 的新函数符号。我们也可以将 \(f_\varphi\) 定义为部分函数，仅在 \(M \models \exists y\, \varphi(y, a_1, \ldots, a_n)\) 时有定义。关键之处在于，\(F\) 是一个预闭包算子，它保证 \(F(A)\) 包含了所有以 \(A\) 中元素为参数并且在 \(M\) 中存在解的公式的解。同时满足： \[ |F(A)| \le |A| + |\sigma| + \aleph_0~ \]

向上部分

　　 首先，通过为 \(M\) 的每一个元素添加一个新的常数符号，扩展签名，得到扩展签名 \(\sigma'\)。在这个扩展签名下，\(M\) 的完整理论称为其初等图像（elementary diagram）。接着，向签名中再加入 \(\kappa\) 个新的常数符号，并向 \(M\) 的初等图像中添加句子 \(c \neq c'\)（其中 \(c, c'\) 是任意两个不同的新常数符号）。根据紧致性定理（compactness theorem），该理论是一致的。由于其模型的基数至少为 \(\kappa\)，根据该定理的 “向下部分”，我们可以得到一个恰好具有基数 \(\kappa\) 的模型 \(N\)。该模型 \(N\) 含有 \(M\) 的一个同构拷贝，且该拷贝是 \(N\) 的一个初等子结构。\(^\text{[6][7]:100–102}\)

4. 在其他逻辑中的情况

　　 尽管经典的洛文海姆–斯科伦定理（Löwenheim–Skolem Theorem）与一阶逻辑（first-order logic）紧密相关，但在其他逻辑系统中仍存在其若干变体。例如，在二阶逻辑（second-order logic）中，每一个一致的理论（consistent theory）都存在一个小于第一个超紧致基数（supercompact cardinal，若其存在）的模型。在某种逻辑中，能够适用 “向下” 洛文海姆–斯科伦型定理的最小基数，称为该逻辑的洛文海姆数（Löwenheim number），它可以用来刻画该逻辑的 “强度”（expressive strength）。此外，当我们超越一阶逻辑时，必须放弃以下三者之一：可数紧致性（countable compactness）；向下洛文海姆–斯科伦定理（downward Löwenheim–Skolem theorem）；抽象逻辑的性质（properties of an abstract logic）。\(^\text{[8]:134 }\)

5. 历史说明

　　 以下叙述主要基于 Dawson（1993）。在理解模型论早期发展史时，需要区分两个概念：语法一致性（syntactical consistency）：即无法通过一阶逻辑的推理规则导出矛盾；可满足性（satisfiability）：即存在某个模型使公式成立。令人惊讶的是，早在完备性定理（completeness theorem）出现、从而使这种区分变得多余之前，“consistent” 一词在文献中有时被用于前者，有时用于后者。

　　 模型论史上的第一个重要成果来自 Leopold Löwenheim（1915），发表于其论文《Über Möglichkeiten im Relativkalkül》（《关于关系演算中的可能性》）：

　　 对任意可数签名 \(\sigma\)，若某个 \(\sigma\)-句子是可满足的，则它在某个可数模型中可满足。

　　 实际上，Löwenheim 的论文讨论的是更一般的 Peirce–Schröder 亲属演算（即带量词的关系代数）。\(^\text{[2]}\) 他使用了现已过时的 Ernst Schröder 符号体系。 若想了解该论文的现代符号摘要，可参见 Brady（2000，第 8 章）。

　　 根据通行的历史观点，Löwenheim 的证明被认为有缺陷，因为他隐含使用了 Kőnig 引理（Kőnig’s lemma）却未加证明—— 而当时该引理尚未正式发表。不过，在修正性研究中，Badesa（2004）认为 Löwenheim 的证明实际上是完备的。

　　 Thoralf Skolem（1920）给出了一个正确的证明，使用了后来被称为斯科伦范式（Skolem normal form）的公式形式，并依赖于选择公理（Axiom of Choice）。他证明了：每一个在模型 \(M\) 中可满足的可数理论，在 \(M\) 的某个可数子结构中也可满足。

　　 随后，Skolem（1922）又在不依赖选择公理的情况下，证明了一个较弱的版本：每一个可数且可满足的理论，也可在某个可数模型中被满足。

　　 Skolem（1929）进一步简化了他 1920 年的证明。

　　 最终，阿纳托利·伊万诺维奇·马尔采夫（Anatoly Ivanovich Maltsev，1936）在其论文中给出了该定理的完全一般形式（Maltsev 1936）。他引用了 Skolem 的一则笔记，称 Alfred Tarski 曾在 1928 年的研讨会上证明了该定理。因此，该定理有时也被称为 Löwenheim–Skolem–Tarski 定理。然而，Tarski 并不记得自己的证明，而他在没有使用紧致性定理的情况下如何做到这一点仍是一个谜。

　　 具有讽刺意味的是，Skolem 的名字不仅与定理的 “向下” 部分有关，也被附在 “向上” 部分上，尽管他本人并不相信该结果：“我依循惯例将推论 6.1.4 称作‘向上洛文海姆–斯科伦定理’，但事实上 Skolem 并不相信它，因为他不相信不可数集的存在。” — Hodges（1993）

　　 “Skolem 拒绝该结果，认为它毫无意义；而 Tarski 则合理地回应说，若从 Skolem 的形式主义立场出发，那么‘向下’洛文海姆–斯科伦定理也应同样被视为毫无意义。” — Hodges（1993）

　　 “传说直到生命的最后，Thoralf Skolem 仍为自己的名字与此类结果相联系而感到震惊，因为他认为‘不可数集’不过是虚构的概念，不具有真实存在。” — Poizat（2000）

6. 参考文献

1. Manzano, María（1996），《Extensions of First Order Logic》，剑桥理论计算机科学丛书第 19 卷，剑桥大学出版社，剑桥，第 5 页，ISBN 0-521-35435-8，MR 1386188。“洛文海姆–斯科伦定理在此也不成立……表达‘宇宙不可数’的公式并没有可数模型，因此无法满足该定理的要求。”
2. Nourani, C. F.，《A Functorial Model Theory: Newer Applications to Algebraic Topology, Descriptive Sets, and Computing Categories Topos》，多伦多：Apple Academic Press；博卡拉顿：CRC Press，2014 年，第 160–162 页。
3. Sheppard, B.，《The Logic of Infinity》，剑桥：剑桥大学出版社，2014 年，第 372 页。
4. Haan, R. de，《Parameterized Complexity in the Polynomial Hierarchy: Extending Parameterized Complexity Theory to Higher Levels of the Hierarchy》，柏林/海德堡：施普林格出版社，2019 年，第 40 页。
5. Bays, T.，“Skolem's Paradox”，载于 Stanford Encyclopedia of Philosophy，2014 年冬季版。
6. Church, A., & Langford, C. H.（编），The Journal of Symbolic Logic，斯托尔斯（康涅狄格州）：符号逻辑协会，1981 年，第 529 页。
7. Leary, C. C., & Kristiansen, L.，《A Friendly Introduction to Mathematical Logic》，纽约州杰内西奥：Milne Library，2015 年，第 100–102 页。
8. Chang, C. C., & Keisler, H. J.，《Model Theory》，第 3 版，米尼奥拉与纽约：Dover Publications，1990 年，第 134 页。

7. 来源

　　 关于洛文海姆–斯科伦定理的讨论，几乎出现在所有模型论或数理逻辑的入门教材中。

历史出版物

• Löwenheim, Leopold（1915），《Über Möglichkeiten im Relativkalkül》，Mathematische Annalen，76 (4): 447–470，doi:10.1007/BF01458217，ISSN 0025-5831，S2CID 116581304。（德文）
• Löwenheim, Leopold（1977），《On possibilities in the calculus of relatives》，收录于 From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931（第 3 版），剑桥（马萨诸塞州）：哈佛大学出版社，第 228–251 页，ISBN 0-674-32449-8。（Google Books 在线版，第 228 页）
• Maltsev, Anatoly Ivanovich（1936），《Untersuchungen aus dem Gebiete der mathematischen Logik》，Matematicheskii Sbornik, Novaya Seriya，1(43)(3): 323–336。
• Skolem, Thoralf（1920），《Logisch-kombinatorische Untersuchungen über die Erfüllbarkeit oder Beweisbarkeit mathematischer Sätze nebst einem Theoreme über dichte Mengen》，Videnskapsselskapet Skrifter, I. Matematisk-naturvidenskabelig Klasse，4: 1–36。
• Skolem, Thoralf（1977），《Logico-combinatorical investigations in the satisfiability or provability of mathematical propositions: A simplified proof of a theorem by L. Löwenheim and generalizations of the theorem》，收录于 From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931（第 3 版），剑桥（马萨诸塞州）：哈佛大学出版社，第 252–263 页，ISBN 0-674-32449-8。（Google Books 在线版，第 252 页）
• Skolem, Thoralf（1922），《Einige Bemerkungen zu axiomatischen Begründung der Mengenlehre》，Matematikerkongressen I Helsingfors den 4–7 Juli 1922, den Femte Skandinaviska Matematikerkongressen, Redogörelse：217–232。
• Skolem, Thoralf（1977），《Some remarks on axiomatized set theory》，收录于 From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931（第 3 版），剑桥（马萨诸塞州）：哈佛大学出版社，第 290–301 页，ISBN 0-674-32449-8。（Google Books 在线版，第 290 页）
• Skolem, Thoralf（1929），《Über einige Grundlagenfragen der Mathematik》，Skrifter Utgitt av Det Norske Videnskaps-Akademi I Oslo, I. Matematisk-naturvidenskabelig Klasse，7: 1–49。
• Veblen, Oswald（1904），《A System of Axioms for Geometry》，Transactions of the American Mathematical Society，5 (3): 343–384，doi:10.2307/1986462，ISSN 0002-9947，JSTOR 1986462。

次级资料

• Badesa, Calixto（2004），《The Birth of Model Theory: Löwenheim's Theorem in the Frame of the Theory of Relatives》，普林斯顿，新泽西：普林斯顿大学出版社，ISBN 978-0-691-05853-5。更简明的版本见：Leila Haaparanta（编）（2009），《The Development of Modern Logic*》，牛津大学出版社，第 9 章，ISBN 978-0-19-513731-6。
• Brady, Geraldine（2000），《From Peirce to Skolem: A Neglected Chapter in the History of Logic》，阿姆斯特丹：Elsevier 出版社，ISBN 978-0-444-50334-3。
• Crossley, J. N., Ash, C. J., Brickhill, C. J., Stillwell, J. C., Williams, N. H.（1972），《What is Mathematical Logic?》，伦敦／牛津／纽约：牛津大学出版社，第 59–60 页，ISBN 0-19-888087-1，Zbl 0251.02001。
• Dawson, John W. Jr.（1993），〈The Compactness of First-Order Logic: From Gödel to Lindström〉，History and Philosophy of Logic，14: 15–37，doi:10.1080/01445349308837208。
• Hodges, Wilfrid（1993），《Model Theory》，剑桥：剑桥大学出版社，ISBN 978-0-521-30442-9。
• Poizat, Bruno（2000），《A Course in Model Theory: An Introduction to Contemporary Mathematical Logic》，柏林／纽约：Springer 出版社，ISBN 978-0-387-98655-5。

8. 外部链接

• Sakharov, A.；Weisstein, E. W.，“Löwenheim–Skolem Theorem”，收录于 MathWorld。
• Burris, Stanley N.，“Contributions of the Logicians, Part II: From Richard Dedekind to Gerhard Gentzen”。
• Burris, Stanley N.，“Downward Löwenheim–Skolem Theorem”。
• Simpson, Stephen G.（1998），《Model Theory》。