首都师范大学 2005 年硕士考试试题

                     

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 一质量为 m、长度为乚的均匀杆，在距离其一端点为 0.2L 处钻一小孔，并将孔穿在一光滑水平轴上，使杆可以在竖直平面内自由摆动。求杆做微幅摆动的周期。
2. 一质量为 m、半径为 R 的圆柱体，放置在一固定斜面上。圆桂体与斜面之间的摩擦系数为μ。将圆柱体放置在斜面上，让其从静止开始向下做无滑滚动。为保证圆柱体不发生滑动，斜面的倾角不能大于多少？
3. 两个滑冰运动员的质量各为 M，以速率 $v_0$ 沿两平行线相对滑行，滑行路线间的垂直距离为 L。当彼此交错时，两运动员各自抓住长度为 L 的绳索的一端，并在相对旋转的过程中各自收拢绳索。求，当绳长为 0.5L 时，他们各自的速率为多少？总动能的变化如何？
4. 一平行板电容器，板面积为 s，间距为 d，接在电源上以保持板间电压为 U。将两板之间距离拉开一倍。求:
   (1)静电能的改变:
   (2)电场对电源所做的功;
   (3)外力对极板所做的功;
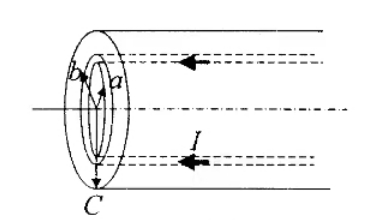
   (4)说明此过程中系统的能量守恒与转化关系。
5. 无穷长载流中空圆管置于真空中(见图 1)，其内、外半径分别为 a,b。管的横截面中电流均匀分布，总电流为 I。管外又包有绝缘层，其外半径为 c。已知圆管和绝缘层的相对磁导率分别为 $\mu_{r1}$ 和 $\mu_{r2}$。求:
   (1)空间各点磁感应 $\vec B$ 的分布;
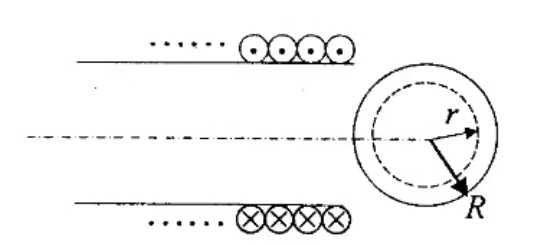
   (2)当 $\mu_{r1}$≈1,$\mu_{r2}$>>1 时磁化面电流的分布。
   
   图 1
6. 在半径为 R 的无限长螺线管中通上电流(见图 2)，当电流随时间发生变化时，在管中产生变化的磁场。若管内磁场的变化率为 $\displaystyle \frac{\mathrm{d}{\vec B}}{\mathrm{d}{t}} $,且 $\displaystyle \frac{\mathrm{d}{\vec B}}{\mathrm{d}{t}} =\vec C$(\vec C 为大于零的常矢量)。求:距离管中心轴线为 r(r<R)处感生电场的大小。
   
   图 2
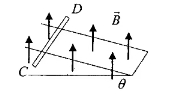
7. 一长为 l，质量为 m 的导体棒 CD，其电阻为 R，沿两条平行导电轨道无擦滑下，轨道电阻不计。轨道与水平面之间夹角为 $\theta $，整个装置放置在均磁场中，场的磁感应强度为 $\vec B_0$(见图 3)求:导体下滑时速度随时间的变化规律。
8. 考虑精细结构，氢原子光谱中帕邢系的第一条谱线应由多少个波长成分组成,试画出相应的精细结构能级跃迁图，并标明各能级对应的原子态符号。
9. 某元素原子光谱中的一条谱线为 $^3D_1 \to ^3P_1$ 跃迁产生，试求:
   (1)在弱磁场 B 中，这两个能级各分裂为几个能级？分裂后相邻能级间隔各为多少 $\mu_B B$？($\mu_B=\frac{eh}{2m_e}$)为玻尔磁子。
   (2)在弱磁场 B 中，该谱线会分裂为多少条(在垂直与平行磁场两方向观察)？与原谱线的波数差各为多少 $\widetilde L$？($\widetilde L=\frac{eB}{4\pi m_e c}$ 为洛伦兹单位）
   (3)画出相应的能级跃迁图。
   
   图 3
10. (1)氢原子与中子质量分别为 1.007825u 和 1.008665u，试计算 $^12_6C$ 原子核的结合能与核子平均结合能.
    (2)从含有 1 克 $^{232}_{90}Th$ 的薄片中测得每秒放射 4100 个α粒子,试计算 $^{232}_{90} Th$ 的半衰期。