上海海事大学 2013 年数据结构
贡献者: xzllxls
1. 一。判断题(本题 10 分,每小题 1 分)
1.数据的逻辑结构说明数据元素之间的顺序关系,它依赖于计算机的存储结构。
2.两个栈共享-片连续内存空间时,为了提高内存利用率,减少溢出机会,应把两个栈的栈底分别设在这片内存空间的两端。
3.线性表若采用链式存储表示时所有结点之间的存储单元地址可连续也可不连续。
4.假定 $n$ 和 $m$ 为二叉树中的两个结点,$m$ 的层数大于 $n$ 的层数,则前序遍历时 $n$ 一定在 $m$ 之后。
5.采用链地址法解决冲突时,若规定插入总是在链首,则插入任一个元素的时间是相同的。
6.在查找树(二叉排序树)中插入一个新结点,总是插入到叶子结点的下面。
7.用邻接矩阵存储一个图时,在不考虑压缩存储的情况下,所占用的存储空间大小与图中顶点的个数有关,而与图的边数无关。
8.排序方法是否稳定的,指的是该方法在各种情况下的时间效率是否相差不大。
9.对大小均为 $n$ 的有序表和无序表进行顺序查找,在等概率查找的情况下,它们对于查找成功的平均查找长度是相同的,而对于查找失败的平均查找长度是不同的。
10.算法分析只要考虑算法的时间复杂度。
2. 二,填空题(本题 30 分,每空 2 分)
1.分析下列程序段,其时间复杂度分别为:((1) )、((2))
i=1;
while (i<=n*n)
i=i+i;
int s=0;
for(i=0; i<n; i++)
for(j=0; j<n; j++)
s+=B[i][j];
sum=s;
2.在一个长度为 $n$ 的顺序表的第 $i$ 个元素(其中 $1\leqslant i\leqslant n$)之前插入一个元素,需要后移((3))个元素。
3.设有一空栈, 现有输入序列 1,2,3,4,5 ,经过 push, push, pop, push, pop, push,push, pop, pop, pop 后,输出序列是((4))。
4.深度为 $k$ 的完全二叉树至少有((5))个结点,至多有((6))个结点,设根结点的层数为 $1$。
5.广义表 $A=((a),((b),c),(((d))))$ 的长度是((7))深度是((8)),取表头和表尾函数分别为 $head()$ 和 $tail()$,则 $head(head(head(tail(A))))$=((9)), 而从表中取出原子项 $c$ 的运算为((10) ).
6.有一个二维数组 $A[1..8]0..5]$,每个数组元素占用 $4$ 个存储单元,并且 $A[3][4]$ 的存储地址为 $1080$, 若按行序为主序方式存储,数组元素 $A[2][3]$ 的存储地址是((11));若按列序为主序方式存储,数组元素 $A[2][3]$ 的存储地址是((12)).
7。一个图的边集为{<a,c>,<a,e>,<c,f>,<d,c>,<e,b>,<e,d>},从顶点 a 出发进行深度优先搜索遍历得到的顶点序列为((13)), 从项点 $a$ 出发进行广度优先搜索逼历得到的顶点序列为((14))。对该图进行拓扑排序得到的顶点序列为((15))。
3. 三,选择题(本题 20 分,每空 2 分)
1 .数据结构是指( )
A) 数据元素的组织形式
B) 数据类型
C) 数据存储结构
D) 数据定义
2.设单链表中指针 $p$ 指向结点 $m$,若要删除 $m$ 之后的结点(若存在),则需修改指针的操作为( )
A) p->next=p->next->next; $\qquad$ B) p=p->next;
C) p=p->next->next; $\qquad$ D) p->next=p;
3.在具有 $n$ 个单元的顺序存储的循环队列中,假定 $front$ 和 $rear$ 分别为队头指针和队尾指针,则判断队满的条件为()
A ) $rear\%n==front$
B ) $(front+1)\%n==rear$
C ) $rear\%n-1==front$
D ) $(rear+1)\%n==front$
4.如果一个栈的进栈序列是 ABCDE(即: A 先进栈,然后 B、C、D 和 E 依次进栈),允许在进栈过程中可以退栈,且规定每个元素进栈和退栈各一次,那么不可能得到的退栈序列是( )
A) ABCDE $\qquad$ B) BCDEA $\qquad$ C) EABCD $\qquad$ D) EDCBA
5.若查找每个元素的概率相等,则在长度为 $n$ 的顺序表上查找任一元素的平均查找长度为( )
A) $n$ $\qquad$ B) $n+1$ $\qquad$ C) $(n-1)/2$ $\qquad$ D) $(n+1)/2$
6.对具有 $n$ 个元素的有序表采用折半查找,则算法的时间复杂度为( )
A) $O(n)$ $\qquad$ B) $O(n^2)$ $\qquad$ C) $O(1)$ $\qquad$ D) $O(log_2n)$
7.假设在一棵二叉树中,双分支结点数为 $15$,单分支结点数为 $30$ 个,则叶子结点数为( )个。
A) 15 $\qquad$ B) 16 $\qquad$ C) 17 $\qquad$ D)47
8.若要把 $n$ 个顶点连接为一个连通图,则至少需要( )条边。
A) $n$ $\qquad$ B) $n+1$ $\qquad$ C) $n-1$ $\qquad$ D) $2n$
9.若要从 $1000$ 个元素中得到 $10$ 个最小值元素,最好采用( )方法。
A)直接插入排序 $\qquad$ B) 简单选择排序 $\qquad$ C) 堆排序 $\qquad$ D)快速排序
10.若一个元素序列基本有序,则选用( )方法较快。
A )直接插入排序 $\qquad$ B) 简单选择排序 $\qquad$ C )堆排序 $\qquad$ D )快速排序
4. 四.应用题(本题 60 分,每小题 10 分)
1.已知某通信系统中可能出现九个字符:C、O、M、P、U、T、E、R、S,它们出现频率分别为: 0.11. 0.09、0.06. 0.15. 0.23、0.12. 0.04、0.03、0.17 ,试利用它们作为叶子结点构造一棵 Huffman 树(哈夫曼树).并设计这些字符的哈夫曼编码。
2.已知一棵二叉树的中序序列和后序序列分别为,
中序序列: DBGKEACHF
后序序列: DKGEBHFCA
请画出该树的结构并写出其先序序列。
3.设散列表为 HT[0..18] ,即表的长度为 19。散列函数为: H(key)=key%19,采用线性探测再散列法解决冲突,若插入的关键码序列为{63, 251, 191, 164, 133, 125, 118,161, 157, 134, 87, 291, 386, 153, 59, 206}。
1)试画出插入这 16 个关键码后的散列表。
2)计算在等概率情况下查找成功的平均查找长度 ASL。
4.对于正整数序列{58, 29, 82, 64, 90, 38, 8,15, 49, 98, 73},建立一棵二叉排序树,然后删除结点 $82$,分别画出该二叉排序树及删除结点 $82$ 后的二叉排序树。
5.已知待排序记录的关键字序列为{248,320,389,183,235,352,266,312,178,257,328,196},需要按关键字值递增的次序进行排序,请分别写出用下列两种排序方法进行第一趟扫描后的结果。
1)以第一个元素为基准的快速排序
2)归并排序
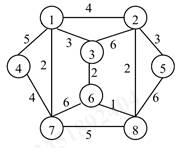
6.右图是一个无向图,试分别用下列两种方法求它的最小生成树,并给出依次产生的边,连接顶点 $i$ 和 $j$ 边用<$i$, $j$>的形式表示。
1)用普里姆算法从顶点 $1$ 开始;
2)用克鲁斯卡尔算法。
5. 五.编程题(本题 30 分,每小题 10 分)
1.编写一个函数计算:
$S=1+(2+3)+(3+4+5)+(4+5+6+7)+...+(50+51+52+..+99)$
2.试设计一个算法,将表头为 $first$ 的单链表中 $data$ 域值最大的结点删除。单链表存储结构为:
typedef struct Node {
ElemType data;
struct Node *next;
} Node,*List;
3.试编写函数计算二叉树中度为 $1$ 的结点的个数。二叉树用二叉链表存储,定义为:
typedef struct BiNode {
ElemType data;
struct BiNode *lchild,*rchild;
}BiNode,*BiTree;