厦门大学 2002 年硕士物理考试试题

                     

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 一质盘为 $m=2kg$ 的质点在 XY 平面内运动，运动方程为:$\bar r =[(-t^3+2t)\bar i+(t^2-3t)\bar j]m$。
   (1)$t=2$(s)时质点所受的合力 $\bar F$=($\qquad$)
   (2)$t=0$(S)至 $t=2$(s)时间内 $\bar F$ 的量 $\bar I$=($\qquad$)
   (3)$t=0$(s)至 $t=2$(s)时间内产所作的功 $W$=($\qquad$)
2. 一平面简谐波以波速 $v=60(m/s)$ 在密度为 $\rho=2.0(kg/m^3)$ 的弹性介质中沿 Y 轴负方向传播，已知平衡位置在 $y=20(m)$ 处的 $P$ 点的振动曲线如图所示。
   (1)该平面简谐波的表达式为($\qquad$)
   (2)该平面简谐波的能流密度大小为($\qquad$)
3. 某气体在 $T=27$°$K,p=1.00atm$ 时的密度 $\rho=1.30kg.m^{-3}$，则该气体单位体积分子数 $n$=($\qquad$),摩尔质量 $\mu$=($\qquad$),分子平均平动动能 $\bar \varepsilon$=($\qquad$),平均速率 $\bar v$=($\qquad$)。
4. 基尔雀夫第一定律的基础是($\qquad$),基尔萑夫第二定律的基础是($\qquad$)。
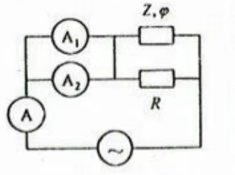
5. 电路如图所示，已知电阻 $R=40\Omega$，三个电流表的读数分别为 $I_1=4.0A,I_2=3.0A,I=6.0A$，则元件乙的功率为($\qquad$)。
   
   图 1
6. 利用消反射膜来消除玻璃镜头的反射光时，通常膜的折射率 n 应($\qquad$)(小于或大于)，玻璃的折射率:膜的最小厚度应等于($\qquad$)。
7. 自然光投射到两片叠在一起的偏振片上，若偏振片是理想的，(1)当透射光是入射光强度的三分之一时，这两偏振片的透光方向的夹角应:($\qquad$)。(2)当透射光是最大透射光强的三分之一时，这两偏振为片的透光方向的夹角应为($\qquad$)。
8. 如图，长为 $l$，质是可忽略的杆上周定有两质盘均为 $m$ 的小球 A,B,A 球位于杆中间，B 球位于杆的一端，系统自水平位置以零初速绕过杆的另一端点 O 的转轴沿竖直而自由下摆。求:
   (1)当杆与水平夹角为 $\theta$ 时，$B$ 球的速度和加速度;
   (2)此时杆对 $B$ 球的作用力;
   (3)系统运动到整直位置时，$B$ 球与一静止的小球 $C$ 发生对心弹性碰撞，碰撤后 $B$ 球(连同 $A$ 球)刚好静止，求小球 $C$ 的质量。