残差网络

贡献者： xzllxls

预备知识　卷积神经网络

　　 残差网络（Resdual network, ResNet）是卷积神经网络的一种常见的变体。与原始的卷积网络所不同的是，残差网络学习的是源数据到源数据与标签之间的残差的映射。

　　在卷积网络的实践中，人们发现了退化（degradation）现象。随着网络深度的增加，模型的准确率会降低，也就是说，较深的网络模型反而比浅层网络有更大的训练误差和测试误差[1]。文献[1]提出的解决方法是增加一条表示恒等映射的短连接（shortcut connections），将浅层网络输出的值通过恒等映射直接传递到深层网络上，从而保证深层网络的误差至少不会超过浅层网络。

　　假设一个残差网络的输入张量为 $ \boldsymbol{\mathbf{x}} $，标签值为 $ \boldsymbol{\mathbf{y}} $，残差网络学习的是 $F: \boldsymbol{\mathbf{x}} \rightarrow \boldsymbol{\mathbf{y}} -x$。数学表达式为：

\begin{equation} \boldsymbol{\mathbf{y}} =F( \boldsymbol{\mathbf{x}} ; \boldsymbol{\mathbf{w}} )+ \boldsymbol{\mathbf{x}} ~. \end{equation}

其中，$ \boldsymbol{\mathbf{x}} $ 和 $ \boldsymbol{\mathbf{y}} $ 分别为输入和输出张量，$F$ 为残差映射，$ \boldsymbol{\mathbf{w}} $ 为权值，其值是学习而来的。

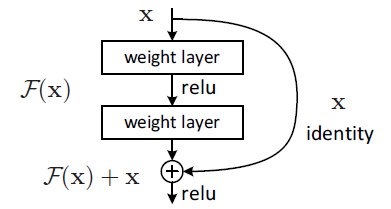
　　为了表示上述数学模型，网络结构方面，采用卷积网络来表示残差映射，短连接来表示关于 $x$ 的恒等映射，最后再将 $ \boldsymbol{\mathbf{x}} $ 与 $F( \boldsymbol{\mathbf{x}} )$ 相加。此处的加法是元素级别（element-wise）对应的张量相加，因此，$ \boldsymbol{\mathbf{x}} $ 和 $F( \boldsymbol{\mathbf{x}} )$ 的维度要相同，否则无法运算。如下图所示：

图 1：残差网络示意图 [1]

　　经过改进之后的网络，即残差网络，消除了原有深层网络的退化现象。经过在 ImageNet 数据集上的实验，发现 34 层的残差网络比 18 层的要有更小的训练误差和测试误差。

　　 参考文献：

S. R. Kaiming He Xiangyu Zhang, “Deep Residual Learning for Image Recognition,” in Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 770–778.