贡献者: 零穹
将图的点集和边集的关系用矩阵来体现,就是所谓的图的矩阵表示。体现点与点相邻关系的矩阵称为邻接矩阵;体现点与边关联关系的矩阵称为关联矩阵。当对某个图选定了权函数成为赋权图时,体现权函数的矩阵称为赋权矩阵。
1. 邻接矩阵
邻接矩阵是用来体现点点相邻关系的,具体地,设图 $G$ 的点集为 $V(G)=\{v_1,\cdots,v_n\}$。若 $G$ 是无向图,则邻接矩阵的第 $(i,j)$ 个元反映了连接 $v_i,v_j$ 的边数。若 $G$ 是有向图,则邻接矩阵的第 $(i,j)$ 个元反映了以 $v_i$ 为起点,$v_j$ 为终点的有向边数。
定义 1 邻接矩阵
设 $G$ 是图,$V(G)=\{v_1,\cdots,v_n\}$,$A=(a_{ij})$ 是 $n$ 阶矩阵。若 $G$ 是无向图,$a_{ij}$ 等于连接 $v_i,v_j$ 的边数;若 $G$ 是有向图,$a_{ij}$ 等于以 $v_i$ 为起点,$v_j$ 为终点的有向边数。则称 $A$ 为 $G$ 的邻接矩阵(adjacency matrix)。
定理 1
设 $A$ 是有向图 $G$ 的邻接矩阵,$V(G)=\{v_1,\cdots,v_n\}$。则 $A^k$ 中的第 $(i,j)$ 元是 $G$ 中长度为 $k$ 的从 $v_i$ 到 $v_j$ 的有向链的数目。
证明:
使用数学归纳法证明如下:当 $k=1$ 是,由邻接矩阵 $A$ 的定义(定义 1 )和链长的定义(定义 1 ),可知定理成立;
设 $k=l$ 时定理成立,那么当 $k=l+1$ 时,设 $a_{ij}^{(l)},a_{ij}^{(l+1)}$ 分别是 $A^{l},A^{l+1}$ 的 $(i,j)$ 元。由于 $A^l=A^{l-1}A$,所以
\begin{equation}
a_{ij}^{(l+1)}=\sum_{m=1}^na_{im}^{(l)}a_{mj}.~
\end{equation}
由假设,$a_{im}^{(l)}$ 是从 $v_i$ 到 $v_m$ 的长为 $l$ 的有向链数,$a_{mj}$ 是从 $v_m$ 到 $v_j$ 的长为 $l$ 的有向链数,于是 $a_{im}^{(l)}a_{mj}$ 是从 $V_i$ 到 $v_m$ 再到 $v_j$ 的长为 $l+1$ 的有向链数。而所有从 $v_i$ 到 $v_j$ 的长为 $l+1$ 的有向链,都是从 $v_i$ 到某个 $v_x$ 的长为 $l$ 的有向链与 $v_x$ 到 $v_j$ 的长为 1 的有向链连接构成。
因此若记 $A_m$ 是从 $V_i$ 到 $v_m$ 再到 $v_j$ 的长为 $l+1$ 的所有有向链的全体,而 $A$ 记为从 $V_i$ 到 $v_j$ 的长为 $l+1$ 的所有有向链的全体,那么
\begin{equation}
A=\bigcup_{m=1}^n A_m.~
\end{equation}
显然 $A_a\cap A_b=\varnothing,a\neq b$,因此
\begin{equation}
\left\lvert A \right\rvert =\sum_{m=1}^n \left\lvert A_m \right\rvert .~
\end{equation}
而 $ \left\lvert A_m \right\rvert =a_{im}^{(l)}a_{mj}$。因此定理得证。
证毕!
这一定理对无向图也是成立的,证明类似。
2. 关联矩阵
关联矩阵是用来体现点边的关联关系的,具体地,设图 $G$ 的点集和边集分别为
\begin{equation}
V(G)=\{v_1,\cdots,v_n\},E(G)=\{e_1,\cdots,e_m\}.~
\end{equation}
若 $G$ 是无向图,则关联矩阵的第 $(i,j)$ 个元反映了 $v_i,e_j$ 是否关联。若 $G$ 是有向图,则关联矩阵的第 $(i,j)$ 个元反映了以 $v_i$ 是 $e_j$ 的起点还是终点。为方便使用 Mathematica 软件进行图论计算起见,我们这里使用 Mathematica 关于图的关联矩阵定义
定义 2 关联矩阵
设 $G$ 是图,$V(G)=\{v_1,\cdots,v_n\},E(G)=\{e_1,\cdots,e_m\}$,$A=(a_{ij})$ 是 $n\times m$ 的矩阵。若
\begin{equation}
a_{ij}=\left\{\begin{aligned}
&0,\quad &&v_i\notin e_j,\\
&1, &&e_j=(*,v_i) \quad or\quad \{v_i,v_k\},i\neq k\\
&-1, &&e_j=(v_i,*) ,\\
&2, &&e_j=(v_i,v_i)
\end{aligned}\right.~
\end{equation}
则称 $A$ 为 $G$ 的
关联矩阵(incidence matrix)。
例 1
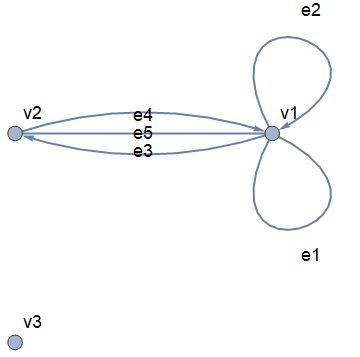
设有图 $G=(V,E,\varphi)$,其中
\begin{equation}
\begin{aligned}
&V=\{v_1,v_2,v_3\},E=\{e_1,e_2,e_3,e_4,e_5\},\\
&\varphi(e_1)=(v_1,v_1), \varphi(e_2)=(v_1,v_1), \\
&\varphi(e_3)=(v_1,v_2), \varphi(e_4)=(v_2,v_1),\varphi(e_5)=\{v_1,v_2\}.
\end{aligned}~
\end{equation}
其中我们定义的 $e_1,e_2$ 尽管都是 $(v_1,v_2)$,但是在 mathematica 中可以将它表示为有向环和无向环
1,因此可以用它们演示 mathematica 中它们在关联矩阵中对应的元是相同的。
该图具有如下的表示
图 1:例子图的表示
那么由关联矩阵定义,该图的关联矩阵为
\begin{equation}
\begin{pmatrix}
2&2&-1&1&1\\
0&0&1&-1&1\\
0&0&0&0&0
\end{pmatrix}.~
\end{equation}
该例的 Mathematica 代码如下,其表明关联矩阵和我们的定义一致。
图 2:代码及结果展示
定理 2
设 $M$ 是图的关联矩阵,则 $MM^T$ 的 $(i,j)$ 元为
\begin{equation}
n_{ij}=\left\{\begin{aligned}
&d_G(v_i)+2r=d_G^+(v_i)+d_G^{-1}(v_i)+2r,\quad &i=j,\\
&-\mu(v_i,v_j)-\mu(v_j,v_i)+\nu(v_i,v_j),\quad &i\neq j.
\end{aligned}\right.~
\end{equation}
其中 $\mu(v_i,v_j)$ 表示以 $v_i$ 为起点 $v_j$ 为终点的边数,$\nu(v_i,v_j)$ 是以 $v_i,v_j$ 为端点的无向边个数。且 $MM^T$ 的第 $i$ 行和 $i$ 列元素之和为
\begin{equation}
4r+2N_i.~
\end{equation}
其中 $N_i$ 是过 $v_i$ 的无向边数。
证明:
设 $N=MM^T$,由于当对某个 $k$ 而言,$M_{ik}M_{jk}$ 在 $i\neq j$ 时,当是有向边 $e_k$ 的两端点时为 -1,当是无向边 $e_k$ 的两端点时 1;而 $M_{ik}M_{ik}$ 为 $e_k$ 的端点且 $e_k$ 不是环时为 1,是环时为 4。因此 $\sum\limits_{k=1}^{ \left\lvert E(G) \right\rvert }M_{ik}M_{jk},i\neq j$ 表示以 $v_i,v_j$ 为端点的边数的负值+该点上 4 倍的环数,$\sum\limits_{k=1}^{ \left\lvert E(G) \right\rvert }M_{ik}M_{ik}$ 表示以 $v_i$ 为端点的边数加上 3 倍的环数,即该点的度加 2 倍的环数。因此,若设 $r$ 是过点 $v_i$ 的环数,则有
\begin{equation}
n_{ij}=\left\{\begin{aligned}
&d_G(v_i)+2r_i=d_G^+(v_i)+d_G^{-1}(v_i)+2r_i,\quad &i=j,\\
&-\mu(v_i,v_j)-\mu(v_j,v_i)+\nu(v_i,v_j),\quad &i\neq j.
\end{aligned}\right.~
\end{equation}
其中 $r_i$ 是过 $v_i$ 的环数,$\mu(v_i,v_j)$ 表示以 $v_i$ 为起点 $v_j$ 为终点的边数,$\nu(v_i,v_j)$ 是以 $v_i,v_j$ 为端点的无向边个数。由 $N$ 的定义知 $N$ 是对称的。且
\begin{equation}
\begin{aligned}
\sum_{j=1}^{ \left\lvert V \right\rvert }n_{ij}&=d_G(v_i)+2r-\sum_{j=1,j\neq i}^{ \left\lvert V \right\rvert } \left(\mu(v_i,v_j)+\mu(v_j,v_i)-\nu(v_i,v_j) \right) \\
&=d_C(v_i)+2r-(d_G(v_i)-2r)+2\sum_{j=1,j\neq i}^{ \left\lvert V \right\rvert }\nu(v_i,v_j)\\
&=4r+2\sum_{j=1,j\neq i}^{ \left\lvert V \right\rvert }\nu(v_i,v_j).
\end{aligned}
~
\end{equation}
例 2
对例 1 的图,有 $d(v_1)=7,d(v_2)=3,d(v_3)=0$,由定理 2 ,可以看出它的关联矩阵和其转置的乘积为
\begin{equation}
\begin{pmatrix}
11&-1&0\\
-1&3&0\\
0&0&0
\end{pmatrix}.~
\end{equation}
使用
定理 2 的结果计算行和得:第一行和为 $4*2+2*1=10$,第 2 行为 $1$,第 3 行为 0。由上面的矩阵可验证这是一致的。
3. 赋权矩阵
赋权矩阵是用来体现赋权函数的,其有不同的定义方式。例如,设图 $G$ 的点集为 $V(G)=\{v_1,\cdots,v_n\}$,则赋权矩阵是一个 $n$ 阶矩阵。若 $G$ 为有向图,则其第 $(i,j)$ 个元反映了以 $v_i$ 为起点 $v_j$ 为终点的所有边的权值之和;若 $G$ 为无向图,则其第 $(i,j)$ 个元反映了连接 $v_i,v_j$ 的所有边的权值之和。
定义 3 赋权矩阵
若 $G$ 是图,$\omega$ 是其上的权函数。则给出权函数的矩阵称为赋权矩阵。
1. ^ 在某些现实的意义上其不是等价的,比如一条以 $a$ 为端点的环,规定只能逆时针走,那么它就是单向的,而若双向可走则才等价于无向环,此时应当由表示顺时针和逆时针的记号进行方向的标记,比如"-",即 $(-a,a)$ 表示逆时针,$(a,-a)$ 表示逆时针。这都是定义的问题,仅仅为了一一对应我们关心的问题,没有标准的表示,只要符合表达了对应关系即可,但是为了方便往往会约定某一种习惯定义,正如我们习惯了集合用花括号定义